基于改进A＊算法的多基地多无人机分阶段任务规划方法

郑 锴，尹 栋，殷少锋，郑献民，林宏旭

（1. 32146部队，焦作 454000；2. 国防科技大学 智能科学学院，长沙 410000）

随着战争形态和作战样式的转变，无人机侦察保障要求越来越高，由重要时节和重点方向侦察转变成全时、全域和多任务侦察[1-3]。单一无人机平台受作用半径、续航时间、实用升限和任务载荷等性能局限，往往难以满足实际应用需求，多无人机协同运用将是未来战场的重要作战样式。多无人机任务规划成为国内外广泛关注的课题[4-6]。

任务分配和航迹规划是多无人机任务规划的关键问题。多无人机任务规划研究，通常将任务规划问题分解成子问题，首先基于近似代价进行层次化的任务分配，而后基于分配方案规划航迹[7-11]。文献[7]针对单基地多无人机协同搜索多目标问题，提出分步组合优化方法，应用聚类方法将MTSP（Multiple Travelling salesman problem）问题分解为多个旅行商（Travelling Salesman Problem, TSP）问题，应用遗传算法求解TSP问题，该方法具有较好的计算优势；文献[8]针对多无人机任务分配问题，将任务分配分解为任务分簇、任务簇分配和簇内分配三个阶段，层次化分配方法具有较好的实时性；文献[9]针对有人/无人任务联盟形成问题，采用任务聚类-平台分配的分阶段策略，分别采用贪心聚类策略和人工蜂群算法求解，仿真验证了该方法的有效性；文献[10]针对多目标群多无人机协同任务规划，提出“双重优化”思想，首先运用贪心算法对各目标群群内的目标进行航路规划，而后运用遗传算法对各目标间的目标进行任务规划。文献[11]应用分层优化法解决多协作无人机任务规划问题，融合Dubins和B样条曲线规划多无人机执行多任务航线，估算可能的任务指派产生的消耗，进行任务分配求解，进而应用高斯伪谱法规划无人机飞行航迹。

在当前任务规划方法的研究中，通常简化了任务分配和航迹规划的耦合关系，采用直线或简单曲线航迹估计任务分配中的代价指标，未考虑环境威胁规避和飞行性能等对航迹影响因素，造成任务分配与实际情况存在冲突，任务规划往往不是最优或次优解。

本文针对多无人机疏散配置在多个基地、协同执行多目标侦察的任务规划应用需求，综合考虑任务分配和航迹规划的航程代价耦合关系，基于改进A*算法预估航程代价矩阵，提出了一种基于改进A*算法的多基地多无人机分阶段任务规划方法。该方法系统地给出了一种多基地多无人机多阶段、层次化的任务规划处理流程，包括区域设置、航程估算、多基地多无人机任务分配、基地内单无人机时序分配、航迹搜索、航迹平滑、局部动态规划等多个阶段。该方法改进了A*算法用于预估航程代价和航迹搜索，改进了K-means算法用于任务聚类分配，将问题化繁为简。

1 原理架构

基于改进A*算法的多基地多无人机分阶段任务规划方法的原理架构，如图1所示。具体表述为：①区域设置。在地理信息系统（Geographic Information System, GIS）中，依次点击确定各基地坐标和任务坐标，确定任务规划区域范围，采用不同几何形状标记威胁区域。②任务分配。航程估算阶段，改进A*算法，构建各基地、各任务点之间的A*预估航程矩阵，从而避免直接应用直线欧式距离导致的任务分配误差。多基地多无人机任务分配阶段，当任务数量多、区域集中分布时，基于改进K-means算法，实现目标区域聚类、各基地聚类目标分配、基地内无人机任务分配等；当任务数量少、疏散分布时，采用深度遍历方法实现精确任务分配。基地内单无人机时序任务分配阶段，基于TSP模型进行求解；③航迹规划。采用改进A*算法搜索并绘制航迹，基于三次B样条曲线进行航迹平滑。④动态任务规划。依据威胁区域和任务目标的变化，确定需要执行动态规划的无人机及其局部规划空间，并针对部分无人机和局部区域进行动态任务分配和航迹规划。

图1 多基地多无人机任务规划的原理框图Fig.1 Mission assignment framework of multi-UAVs deployed in different bases

2 区域设置

2.1 区域规划

在地理信息系统中，点击选定并标注多基地、多任务的位置，按点击次序为每个基地和任务编号，确定任务规划的区域范围。规划区域如图2所示，设各基地和任务的最大位置高斯坐标值分别为Xmax、Ymax，最小位置高斯坐标值分别Xmin、Ymin，规划空间的扩展距离值为H。将规划空间离散栅格化，（Xmin-H,Ymin-H)为原点，设h为网格边长，则规划空间中任意点（x,y）的网格坐标（xg, yg）为：

图2 规划空间示意图Fig.2 Schematic diagram of plan area

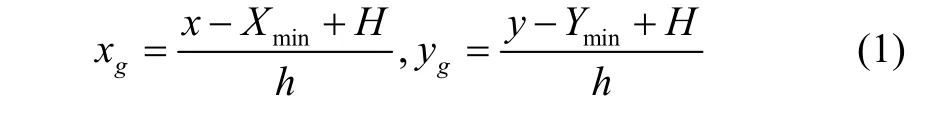
2.2 威胁设置

基于基础地理信息和战场态势信息，在GIS中标绘出地形障碍、雷达探测、电子对抗、防空火力、禁飞区等飞行威胁区域。根据不同威胁模型的特点，在GIS系统中通过手绘或标注等形式，标记出圆形、矩形、多边形等任意不同形状的威胁区域，并按式(1)计算威胁区域边界的网格坐标。

3 任务分配

3.1 改进A*算法设计

A*算法全局性好、运行较快、易于工程实现，在航迹规划领域获得了广泛关注[12-15]。在任务分配过程中，在考虑距离代价时通常用直线欧式距离近似表示航程，没有考虑威胁区域等约束条件对航程的影响，易于造成任务规划不合理，因此可通过A*算法预估各基地与各个任务点、各个任务点之间的距离，将A*预估距离作为任务分配的航程代价。此外，在航迹规划过程中，A*算法用于实现各基地、各任务点间的航迹搜索。

A*算法的代价函数表示为：

式中，n为当前节点，f(n)为起始点经节点n到目标点的代价函数，g(n)为从起始点到节点n的实际代价，h(n)为节点n到目标点的估计代价。

代价函数g(n)可表示为：

式中，ln为航程代价，Jn为威胁代价，zn为高度代价，ω1、ω2和ω3分别表示航迹代价权值。为确保无人机航迹能够规避所有威胁区域，将威胁代价设为无穷大，令ω2=∞；无人机通常优先采用固定高度巡航，为简化航迹优化问题、减少计算量，设无人机以固定高度巡飞，将三维空间航迹搜索问题简化为二维问题，令ω1=1，ω3=0。

启发函数h(n)，引导节点(xn,yn)向目标点(xt,yt)的方向搜索扩展，可表示为：

传统A*算法在栅格节点扩展过程中，节点扩展主要局限在栅格线的交叉点上，可能会导致部分航迹呈锯齿状。为了避免锯齿型航迹，改进A*算法，进行航迹节点再调整，优化部分锯齿型航迹。

图3所示为节点再调整示意图，将虚线航迹优化为实线航迹。设无人机w初始航迹节点序列vw1[r]，节点序列数量为r，则节点再调整过程为：a. 初始令j=r；b. 循环检查（vw1[i],vw1[j]）之间的连线是否通过威胁区，i∊[1…j-1]；若通过威胁区，令i=i+1；若不通过威胁区，令j=i，并将vw1[j]保存为再调整后的航迹节点；c. 重复上述循环，直至j=1，停止循环，生成再调整后的航迹序列vw2[l]，调整后的节点序列数量为l。

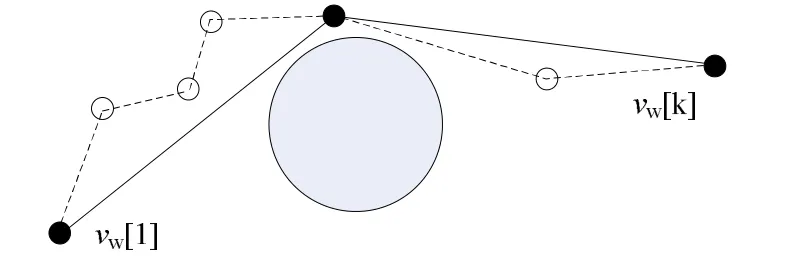
图3 航迹节点调整示意图Fig.3 Schematic diagram of path optimization

图4所示为改进A*算法的主要处理流程。在启发式搜索时，建立OPEN和CLOSE两个表，OPEN表用于存储已经计算但没有扩展的节点，CLOSE表用于存储已经扩展的节点。数据存储结构表示为{（x i,y i）,f i,g i,hi,pi}，其中，(xi,yi)为节点的网格坐标，fi、gi、hi分别为代价函数的变量值，pi代表当前节点的父节点。具体表述为：

图4 改进A*算法流程图Fig.4 The framework of improved A* algorithm

步骤1 初始化。初始化OPEN和CLOSE表，将起点放入OPEN表中作为当前节点。

步骤2 节点扩展与存储。当前节点的相邻节点，若满足约束条件且不在当前OPEN和CLOSE表中，则将该有效节点加入OPEN表；将OPEN表中代价最小的节点A移到CLOSE表；判断节点A是否为终点，若是终点则退出节点搜索，若不是终点则继续节点扩展。从CLOSE表中提取航迹节点序列vw1[r]，将终点的代价函数值作为预估A*航程。

步骤3 航迹节点调整。设vw1[r]中的航迹起点为调整起点，初始航迹终点作为调整中继点；从调整起点开始，依次判断vw1[r]中各航迹点与调整中继点的连线是否经过威胁区域；若调整起点与调整中继点连线通过威胁区域，则将当前调整起点的下一点更新为调整起点，并继续判断是否通过威胁区域；若调整起点与调整中继点连线不通过威胁区域，将当前调整中继点保存为航迹调整后的一个航程点，并将当前调整起点更新为调整中继点，继续循环判断；直至当前调整中继点为起点，停止循环，则各个调整中继点构建出调整后的航迹序列vw2[l]。

通过改进A*算法，分别以各基地和任务点为起止点，启发式搜索航迹，并估算各基地与各个任务点、各个任务点之间的A*预估航程距离。

3.2 多基地多无人机任务分配

设基地序列为P={P1,P2,P3…Pn}，基地数量为n；任务目标序列为T={T1,T2,T3…Tm}，任务数量为m；构建距离矩阵d[n][m]，用于表示每个基地距离每一目标的A*距离；构建距离矩阵表示为q[m][m]，用于表示任两个目标之间的A*距离；各基地无人机数量序列为U={U1,U2,U3…Un}，用于表示各个基地配置的无人机数量。

图5所示为多基地无人机任务分配编码示意图，确保每项任务均有无人机负责执行。

图5 多基地多无人机任务分配编码示意图Fig.5 Schematic diagram of mission assignment coding

根据任务数量和分布情况，多无人机任务分配可以区分两种情况求解：①任务数量多、区域集中分布时，采用基于目标聚类的求解方法。该方法包括目标区域聚类、聚类目标分配、基地内无人机任务分配等多个处理环节，可将较大规模的目标分配问题化繁为简、时效性和可扩展性好；②任务数量少、疏散分布时，采用基于深度遍历的求解方法。该方法适用于计算规模小、目标聚类初始参数难以确定等情况，简化了求解过程，直接采用深度遍历方法进行精确任务分配。

3.2.1 基于目标聚类的求解方法

基于目标聚类的求解方法包括三个处理环节：目标区域聚类、聚类目标分配、基地内无人机任务分配等。目标区域聚类，是实现目标按地理分布集聚特性进行区域聚类；聚类目标分配，是实现将各个聚类目标区域分配给距离最近的无人机基地；基地内无人机任务分配，是实现无人机基地内多架无人机的目标分配。

K-means聚类算法是一种迭代求解的聚类分析方法，其原理简单、收敛速度快、实用性好[16,17]。采用各目标间距离作为相似性评价指标，通过多轮循环迭代，最终确定K个紧凑且相对独立的目标聚类。需要注意的是，由于无人机基地的异构性，各无人机基地配备的无人机数量和型号不同，因此聚类目标不应超出其距离最近基地的任务能力值，需要关注各基地的总任务航程这一约束条件。

结合具体应用背景，在初始聚类中心选取、添加任务总航程约束、确定聚类目标对应的基地等方面，对传统K-means算法进行改进。改进K-means聚类算法的处理流程，如图6所示为：

图6 改进K-means聚类算法的流程图Fig.6 The framework of improved K-means algorithm

步骤1 目标聚类初始化。选取K个位置分散的目标点为初始聚类中心。传统的随机选取初始聚类中心的方法，容易导致聚类效果不佳，因此根据GIS系统上各位置点的分布，手动点击选择K个相对离散、可能接近目标区域中心的位置点，作为初始聚类中心点；

步骤2 确定无人机基地与目标聚类的对应关系。将无人机基地分配给距离最近的聚类中心点；

步骤3 循环目标聚类。循环计算各目标点到各个聚类中心的距离，将每个目标划入其距离最近的目标区域类中。为避免聚类区域的目标数量超出距离最近基地的任务能力，基于航程代价进行判断。若随机选取一个聚类目标序列，其与对应基地之间总航程超过基地内所有无人机最大航程，则从该目标类中选择距离邻近目标聚类中心最近的一个目标，将该目标加入邻近目标聚类中；

步骤4 更新目标聚类中心点。根据所有数据点的平均距离值计算区域质心位置，将聚类中心调整至各区域类的中心目标点；

步骤5 重复步骤2、3和4，直至聚类中心不再变化或达到最大的迭代次数。

通过改进后的K-means目标聚类方法，实现目标区域聚类和聚类目标分配等两种功能，将目标按地理分布分成任务区域、并将任务区域分配给距离最近的无人机基地。

单个基地内的无人机任务分配，若单架无人机能够完成任务，则优先使用单无人机执行；若单架次无人机无法完成所有任务，则结合执行任务的总航程和单机的最大航程，估算出所需的无人机数量，进而采用K-means聚类方法进行基地内的多无人机任务分配。最终为每架无人机分配任务，第w架无人机对应的任务分组为hw[k]。

3.2.2 基于深度遍历的求解方法

任务数量少、疏散分布时，通常计算规模较小，可简化求解环节，直接采用深度遍历方法进行精确任务分配。为每个基地分配距离最近的目标，目标函数Z表示为：

其中，dij为无人机i到目标j的A*距离。

约束条件为：①最大航程约束。单个基地的无人机执行多任务的总航程不能超出其最大航程Lmax。②任务约束。每个基地一架无人机参与任务，每个目标至少有一架无人机去执行任务。

深度遍历精确求解的流程表述为：

步骤1 按照目标序列T的编号，从第一个目标开始依次循环；对比目标与每个无人机基地的距离，选择出距离当前目标最近的无人机基地；依次循环比较，最终确定与目标序列T对应的无人机基地序列，设为H={H1,H2,H3…Hm}。

步骤2 结合序列T和H的对应关系，为每架无人机分配任务，获得第w架无人机对应的任务分组为hw[k]。

3.3 基地内单无人机时序任务分配

在多基地无人机任务分配方案中，若单个无人机分配了多项任务，则需进行单无人机多任务时序分配。单无人机时序任务分配，采用了TSP旅行商模型。传统的TSP模型求解时，在计算各路径点之间的距离时，通常是将各点之间距离简化为直线欧式距离[18,19]。在复杂高对抗的战场环境下，目标点间距离若不考虑规避威胁区域，将存在较大的误差，TSP求解将难以获取合理的结果。因此，改进传统TSP求解方法，任意两点的距离采用A*算法预估距离。

充分考虑规避威胁区域，采用A*算法估算出无人机起飞点、多个任务目标点之间的距离。对于第w架无人机，其对应的任务分组为hw[k]，构建出A*距离矩阵表示为pw[k][k]，k为第w架无人机的对应任务数。

目标函数R表示为：

其中，hij为无人机从目标i到目标j的A*距离，cij∊{0,1}为决策变量。

若时序任务分配规模较小，优先采用遍历法，循环比较任何一种可能方案，准确获得最优解。若时序任务分配规模较大，精确算法求解计算量过大，采用遗传算法求解[20]。

4 航迹规划

4.1 航迹寻优

基于多无人机任务分配和单机时序任务分配的分配方案，依据每架无人机的任务序列分别进行航迹规划，应用改进A*算法进行航迹寻优。A*算法按照3.1执行。

以第w架无人机为例，无人机w的起点、时序序列uw[k]中的各任务点、无人机w的回收点构成航迹点序列，从起点开始，依次将航迹序列中的两个连续时序节点作为A*搜索的起止点，获得各连续节点之间的初始航迹序列vw1[r]、及调整后航迹序列vw2[l]。任意两个时序连续节点间的vw2[l]，组合在一起最终构成第w架无人机的总航迹vw3[q]，总航迹点数量为q。

将无人机的航迹点vw3[q]，进行地理坐标转换，绘制在地理信息系统上，可得到无人机航迹图。依次绘制每架无人机的航迹点，得到多基地多无人机的航迹规划图。

4.2 航迹平滑

航迹寻优绘制的航迹为折线图，不符合实际航迹，需要进行航迹平滑处理，得出满足飞行约束的航迹曲线。三次B样条曲线具有局部性、凸包性和C2连续性等特点，平滑效果好[21]。

基于A*算法航迹寻优获得的航迹控制点为Pi(i=0,1 …n)，采用三次B样条曲线进行平滑处理，每段曲线由连续相邻4个航迹控制点确定。三次B样条曲线可表示为：

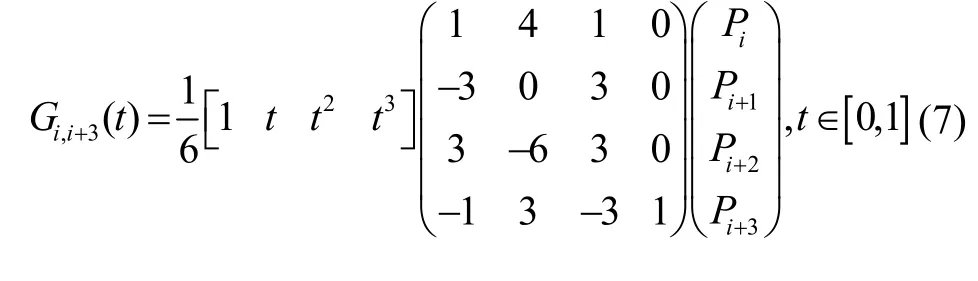
5 局部动态任务规划

在复杂多变的战场环境中，往往存在突发威胁、目标变化等情况，全局规划航迹将不能满足任务的动态需求。根据战场态势变化，在预先全局规划的基础上，仅进行局部动态规划，从而可缩小规划空间、减少规划时间。具体表述如下：

①局部区域设置。根据威胁区域和目标变化情况，在GIS中点击选定局部规划的起点、多个目标点、终止点的位置，标绘局部威胁区域，确定局部规划空间。初始点和终止点通常选在威胁区域边界附近的预先规划航迹上，中间点为无人机必须经过的一些目标点，包括预先已知目标点和动态变化的目标点。

②局部任务动态分配。依据改进A*算法，构建局部规划起点、多个目标点、终止点之间的A*预估航程矩阵；基于旅行商模型和遗传算法，求解各点的时序任务分配。

③局部航迹动态规划。采用改进A*算法规划并绘制航迹，基于三次B样条曲线法进行航迹平滑，规划出局部起点、各中间点、终止点之间的航迹。

6 实验验证

针对多无人机任务规划的应用需求，采用Visual Studio 2015与QT5.8开发环境、以及C++编程语言，基于本文提出的任务规划方法，开发了多无人机任务规划软件。图7所示为任务规划软件的主界面，软件界面主要包括菜单栏、GIS显示区域、状态显示区域、任务规划子界面等，任务规划子界面包括基本设置（网格设置、标绘设置、分配设置等）、任务规划按键（位置选取、区域设定、威胁标绘等）、以及任务显示区域。

任务规划测试的主要操作流程为：输入或选取各初始设置参数；依次点击无人机选取、目标选取、区域设定、威胁标绘、威胁确定等按键，并相应在GIS区域点击确定各位置点、绘制威胁区域，实现规划区域设置；点击航程估算、聚类选取、目标聚类、任务分配等按键，实现任务分配，分配结果以图示形式在任务显示区域显示；点击航迹搜索、航迹调整和航迹平滑等按键，航迹规划结果在GIS界面中绘制并显示。

测试1 基于改进K-means聚类求解的分阶段任务规划流程测试。按照任务规划处理流程，逐步骤进行分析验证，多基地多无人机任务分配阶段采用K-means聚类的方法求解。

（1）参数设置

规划区域内包括3个无人机基地和18个目标，规划空间约80 km×70 km，网格边长h为1 km，扩展距离H为20 km，无人机最大航程200 km。

（2）测试结果分析

图7(a)所示为，分别在GIS中点击确定了无人机基地和目标的位置，目标分布呈现区域集中的分布态势，以手绘形式标记出任意形状的多个威胁区域，点击“航程估算”预估出各个位置点之间A*航程，点击“聚类选取”确定了3个目标初始聚类中心，GIS区域的实心圆点表示初始聚类中心；图7(b)所示为，点击“目标聚类”实现目标区域聚簇，GIS区域的实心圆点分别为初始聚类中心及K-means聚类后的中心，点击“任务分配”，将3个聚类目标群分配至3个无人机基地，分配结果显示在任务显示区域；图7(c)所示为，点击“航迹搜索”后，在GIS区域绘制出各无人机与其时序任务之间的A*搜索航迹，可以看出航迹能够规避障碍，但由于A*搜索局限在栅格交叉点而导致部分航迹呈锯齿状；图7(d)所示为，点击“航迹调整”后，绘制出调整优化后的航迹，将部分A*搜索锯齿型折线航迹段优化为直线；图7(e)所示为，点击“航迹平滑”后，在GIS区域绘制出B样条平滑航迹；图7(f)所示为，分别在局部区域标志出局部起点、2个中间点、局部终点，标绘更新后的威胁区域，在动态规划子界面，点击“任务分配”，求出时序任务分配结果；点击“航迹搜索、航迹调整、航迹平滑”后，规划出局部动态航迹曲线。

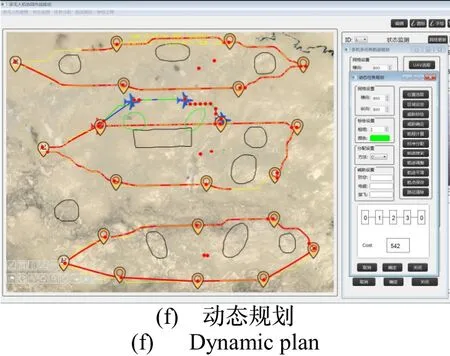
图7 基于K-means聚类求解的任务规划测试Fig.7 Mission plan test with K-means algorithm

测试结果表明，目标聚簇分配和目标时序分配合理，航迹规避了障碍区域，通过航迹调整和航迹平滑优化了复杂威胁条件下无人机航迹，动态任务规划结果合理，测试过程计算无明显时延。

测试2 基于深度遍历求解的分阶段任务规划流程测试。按照任务规划处理流程，逐步骤进行分析验证，多无人机任务分配阶段采用深度遍历方法求解。

（1）参数设置

规划区域内包括5个无人机基地和7个目标，规划空间约80 km×70 km，网格边长h为1 km，扩展距离H为20 km，无人机最大航程200 km。

（2）测试结果分析

图8(a)所示为，分别在GIS中点击确定了无人机基地和目标位置，目标数量较少、呈疏散分布态势，以手绘形式标记出任意形状的多个威胁区域，点击“航程估算”预估出各个位置点之间A*航程，点击“任务分配”为每个目标分配无人机，2个无人机基地参与执行任务，分配结果显示在任务显示区域；图8(b)所示为，点击“航迹搜索”，在GIS区域绘制出各无人机与其时序任务之间的A*搜索航迹；图8(c)所示为，点击“航迹调整”，将部分A*搜索锯齿型折线航迹段进行优化；图8(d)所示为，点击“航迹平滑”后，在GIS区域绘制出B样条平滑航迹。图8(e)所示为，分别标记2组局部起点、中间点、局部终点，标绘更新威胁区域，点击“任务分配”，求出任务分配结果；点击“航迹搜索、航迹调整、航迹平滑”，规划出2组局部动态航迹曲线。

图8 基于深度遍历求解的任务规划测试Fig.8 Mission plan with depth first search algorithm

测试表明，疏散分布的目标合理分配至各无人机基地，各无人机航迹有效规避了威胁区，通过航迹调整和航迹平滑优化了复杂威胁条件下的无人机航迹。动态任务规划结果合理，测试过程无明显时延。

测试3 传统A*算法和改进A*算法的比较分析。结合测试1中的图7(c)和7(d)进行比较分析，图7(c)所示为按照传统A*算法绘制的航迹，图7(d)所示为按照本文改进A*算法绘制的航迹。表1所示为改进A*算法的比较分析表，给出了传统A*和改进A*算法的航迹参数表。

表1 改进A*算法的比较分析Tab.1 Comparison of improved A＊ algorithm

通过比较表明，改进A*算法有效滤除了冗余航迹节点，抑制了锯齿形搜索航迹，缩短了无人机航程，航程缩短了4%以上。进而易于通过航迹平滑获取优化航迹。

测试4 应用改进A*预估距离与欧式预估距离的任务规划比较分析。图9所示为应用欧式预估距离的任务规划测试结果，在任务分配过程中的航程代价均应用欧式直线距离。图10所示为本文所提出方法的测试结果，在任务分配过程中的航程代价均应用改进A*预估距离。多基地多无人机任务分配阶段采用改进K-means聚类的方法求解。表2所示为应用改进A*预估距离的任务规划比较分析表，给出了两种方法的测试结果。

图9 应用欧式预估距离的任务规划测试Fig.9 Mission plan with Euclidean estimated route

图10 应用改进A*预估距离的任务规划测试Fig.10 Mission plan with improved A* estimated route

表2 应用改进A*预估距离的任务规划比较分析Tab.2 Comparison of mission plan with improved A＊route

通过比较表明，应用改进A*预估距离时，在目标区域聚类、聚类目标分配阶段中，均能够顾及威胁障碍区对于预估距离的影响，而直线欧式预估距离无法考虑障碍区影响，应用改进A*预估距离的任务规划具有更短的航程。航程缩短了12%。

7 结 论

本文系统地给出了一种多基地无人机多阶段、层次化的任务规划处理流程，开发了多无人机任务规划软件，验证了所提出方法的有效性。主要结论如下：（1）改进了传统A*算法，通过航迹调整，剔除冗余节点，将节点栅格扩展的锯齿型折线优化为直线航迹；（2）考虑任务分配和航迹规划的航程耦合关系，在多阶段任务分配中，应用改进A*算法预估航程矩阵，生成满足威胁规避和飞行性能约束的任务分配方案；

（3）在初始聚类中心选取、添加任务总航程约束、确定聚类目标对应的基地等方面，改进传统的K-means算法，实现了目标区域聚类和聚类目标分配等功能。

本文方法主要适用于静态确定威胁环境，对于动态不确定环境适应性不强。下一步，需要结合动态不确定的战场威胁、任务变更、飞机损毁等对抗性行动展开研究，精确评估威胁模型和威胁度，针对多种不确定要素进行综合任务规划，提高对抗性环境下任务规划方法的实用性。