复合泊松过程在新疆地震研究中的应用
卢芸潇,刘 淼,2*
(1.伊犁师范大学数学与统计学院,新疆伊宁 835000;2.伊犁师范大学应用数学研究所,新疆伊宁 835000)
0 引言
地震是大自然最可怕和最具破坏性的灾难之一.伴随地震的发生,同时可能会造成许多伤亡和广泛的财产损失.新疆处于印度板块和欧亚板块结合的部分,是地震频发地区.
不少学者研究表明,在某一区域或地震带上地震会按照一定时间间隔规律地复现.因此,对于新疆地区地震复发周期,以及各级地震的发生概率的研究成为地震活动规律分析的一个非常重要的方向.根据相关资料,在1980年至2018年期间影响居住地区的地震占比急剧增加.这些研究引导我们思考是否也可以通过对新疆地区地震的研究对新疆地震的危险性进行一定的评估.我们在假设年度地震发生状况为具有泊松随机变量序列的情况下,对搜集到的新疆地区的地震相关数据集进行了检验.在此假设下,再次得到地震的重现期,并且计算出各级地震的发生概率.
1 基本假设
1.1 预备知识

1.2 震级的分布

1.3 主要结论
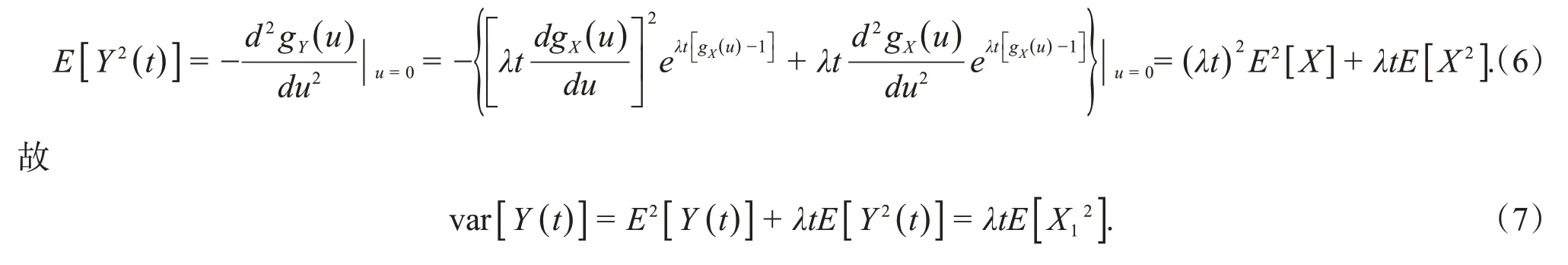
2 实证分析
2.1 新疆历年地震数据
收集《新疆统计年鉴》相关数据,并绘制统计图如图1所示.
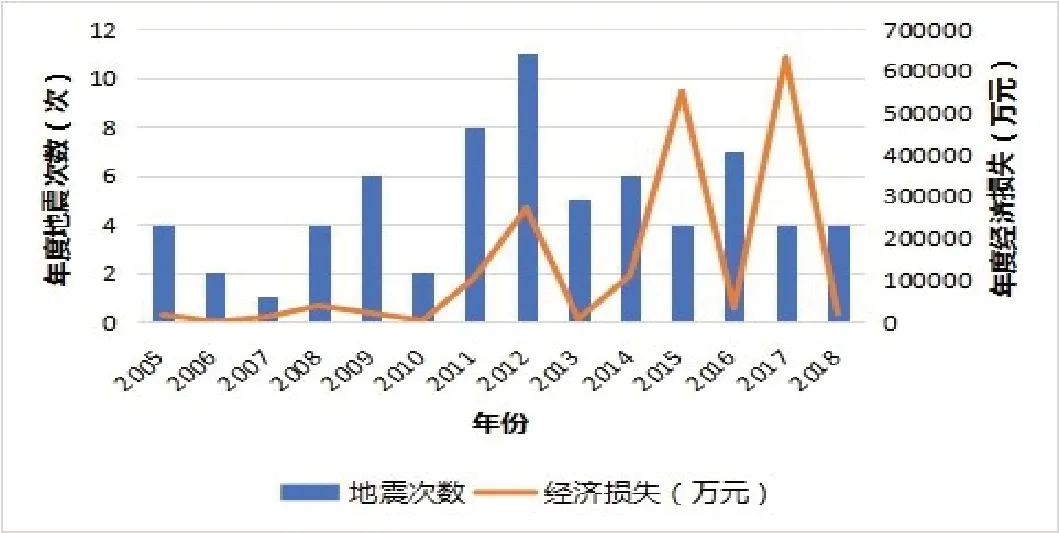
图1 新疆年度地震次数及经济损失
从图1中可以看到,从2005~2018年,新疆共发生68次5级以上地震,每次地震都造成了不少的经济损失.
2.2 模型的建立

2.3 模型的检验
从《新疆统计年鉴》收集数据,制作出新疆地震数据的频率分布表见表1.

表1 按照震级计算的总地震频率
通过拟合优度检验,将观测到的频率分布与理论泊松分布进行比较,计算得P值为0.998,因此可得出接受原假设的结论,这意味着没有显著性差异.地震频率具有泊松分布,平均值为λ = 4.86(年)和λ= 0.013(天).
2005~2018年期间新疆发生的地震频率按震级的分布记录于表2.

表2 新疆地震的频率分布
2005~2018年期间新疆地震发生的频率与震级分布见表2,数据分为3类.
利用χ2拟合优度检验对新疆地震的频率分布和理论指数分布进行拟合优度检验.其中预期频率由1.2中的公式计算得到.对如下原假设与备择假设进行假设检验:
H0:实验分布与理论指数分布没有显著差异.
H1:实验分布与理论指数分布存在显著差异.
预期的概率值和观测的概率值如表3所示.χ2值计算为0.252(P>0.05).因此在0.05的显著水平下不拒绝原假设,即表明震级随机变量具有指数分布.

表3 实验值与理论分布值
2.4 新疆地震复现周期的估计
本文统计了2005~2018年新疆地区的68次5级以上(M≥5)地震的资料,将m的平均值作为一个期望值,计算得到.θ= 5.0是按照震级分类的第一个类别的下界.由公式

计算得到

因此密度函数可以定义为

对密度函数进行积分,得到随机变量的概率密度为

根据不同地震类型划分,得到不同震级的理论与实验值见表3.
计算不同地震类型的平均复发周期如表4所示.

表4 新疆地震复现周期的估计
在本节中,地震的复发周期以年为单位.fM(m)中的数据表示某一确定震级的地震发生概率.表4中的第4列的值表示地震次数的年度期望值,这是由fM(m)所在的列的概率乘以(震级M≥5)地震年度观测频率所得,由表4可以看出5.5级地震的重现期约为每年3次;6.5级地震的重现期约为每年2次;7.5级地震的重现期约为每年1次.表4中的最后一列,表示某一确定震级的地震重现周期.年度复发时间的计算公式如下[3]:

其中,α表示年度复发时间;β表示以年为单位的地震发生频率.
2.5 新疆地震经济损失的期望值

2.6 新疆地震复发概率的估计
上述两式计算得到的概率值分别见表5、表6.
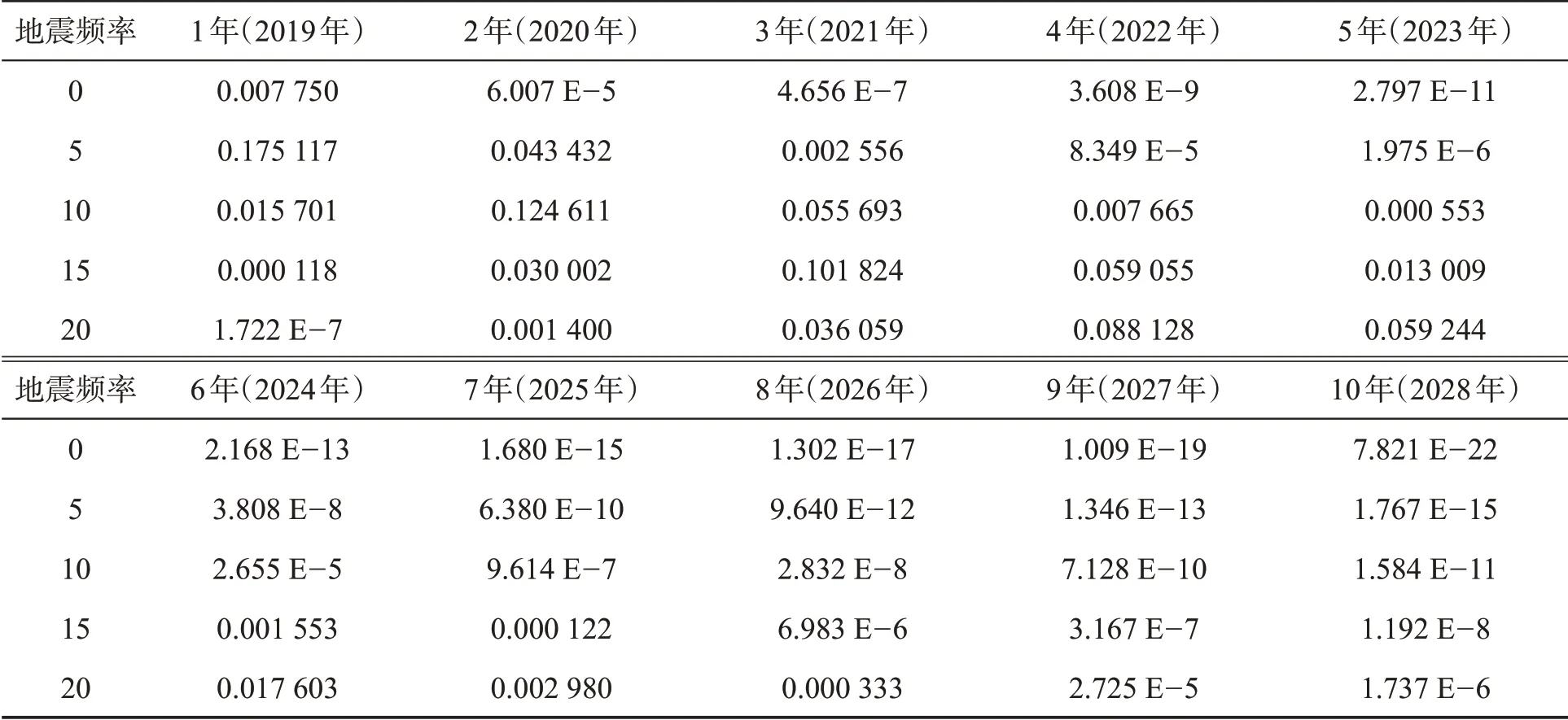
表6 以年为单位估计地震复现概率
从表5可以发现,新疆地区60天0次地震复发的概率为0.4584;180天2次地震复发的概率为0.2637;365天7次地震复发的概率为0.093.
根据表6中的结果可得,1年期间5次地震复发的概率为0.1751;5年期间15次地震复发的概率为0.013.
表7、表8分别给出了以天为单位和以年为单位的期望值.

表7 以天为单位的期望值

表8 以年为单位的期望值
从表7可以看出,预计到2019年3月1日将发生大约1次(0.78)5级及以上地震;类似地,预计到2019年10月26日将发生4次(3.9)5级及以上地震.在表8中可以看出,预计到2020年将发生10次(9.72)5级及以上地震;预计到2026年将发生约39次(38.88)5级及以上地震.
3 结束语
本文搜集到新疆地区2005~2018年5级以上地震的相关数据,利用泊松过程的相关知识建立了数学模型,证明了地震的发生是强度均匀的泊松过程,并用拟合优度检验,表明震级随机变量具有指数分布.采用复合泊松过程对地震期间经济损失的期望值进行了估计,结果表明:t时间内新疆地区地震所造成经济损失的期望值为363.7346t.此外,根据年份和天数,对新疆地区未来一段时间内的地震复现周期和复发概率进行了计算,得到了某些震级的地震重现期和复发概率的估计值.结果表明,5.5级地震的重现期约为每年3次.通过以上分析得出的结果可为今后新疆地震灾害的预防提供一定的理论参考.

