基于CFD的在役飞机电接触致热效应计算方法

于向阳，冉澳，崔璨，徐宁，卢玲

1. 海军航空大学青岛校区，山东 青岛 266041

2. 武警工程大学 信息工程学院，陕西 西安 710086

随着现代航空装备自动化和电气化水平的不断提升，电接触在电气设备及电力电子器件中广泛存在且“控制中枢”地位彰显[1]。近年来，海军航空装备工作环境由岸基走向舰基，其高温、高湿、高盐的海洋环境特点显著，电接触部位电腐蚀、热老化等隐性故障随之而生，并严重制约着系统的运行质量和安全。飞机各系统电子元件的发展呈现小型化、功耗高的趋势，各个组成部分热流量密度急剧上升。相关学者[2-3]认为，随着温度的增加，电接触损坏电子设备和电子设备电接触失效概率的上升趋势大幅增加，在环境温度每升高10℃时，相关电子器件失效率升高为原来2倍以上。根据数据调查，电子设备有55%的失效率是温度超过相关的规定值导致的[4]；过高的温升会迅速引起金属表面的电接触点发生软化，甚至使得金属发生沸腾，造成金属界面迅速地熔结，相互之间发生导体材料迁移，加速电接触连接磨损、氧化[5]。

此外，因为电接触温度升高，接触电阻增大，更多的热量就会因为更大的接触电阻而产生，这种循环对于系统的安全性与可靠性是致命的，给飞机的安全起降带来了巨大的安全隐患。电气系统的相关研究数据显示，电接触失效的因素有很多，但是80%以至更多的因素是电接触在触头处的接触电阻过大；电接触的触点因为尘土或者液体侵入，以及包裹的绝缘材料破损等原因造成电接触发热，进一步导致电接触触点熔焊；其中温度引起故障的百分比达到了40%，占比最大，也表现了温度在引起电接触故障，影响电接触可靠性方面扮演者着重要的作用[4-9]。

电接触致热效应是影响在役飞机电接触可靠性的一个重要因素，一个可行的计算电接触致热的方法，使我们掌握电接触热效应空间分布规律。国内外相关领域的研究大多集中于实验方法，通过安装传感器或红外相机等非接触的方法[10]，获取表面流场分布，分析电接触致热与外部环境的关系。但传感器的存在会破坏电接触周围的流场分布，非接触式的温度获取方法受可达性的限制，对于很多处于封闭空间内部的电接触热场分布无法直接检测。而接触器等大功率电气控制器件的电接触部位，往往存在于非金属材料构成的封闭体中，其致热温度场分布更加复杂，电接触致热导致的温升对电接触及系统可靠性有着更为显著的影响[11-12]。在役飞机电接触型号、数量繁多，分布范围广，且实际工况中不能单独存在，往往作为器件的一部分来发挥功效。考虑到长时间工作的可靠性，大功率接触器件多以双接触体桥式结构存在，同时满足结构适应性需求，含有电接触部位的接触体，往往外形复杂，加之外部封闭体的存在，使得其环境耦合致热流场形成较为复杂的三维分布态势[13-14]。本文将计算流体力学（computational fluid dynamics, CFD）与实验方法相结合，针对封闭体-电接触致热效应，分析其温度流场分布，探究CFD方法的影响因素并验证其有效性，为电接触可靠性分析及失效预先判断开展有益探索。

1 圆柱固定面接触模型致热流场计算

圆柱固定面接触作为大功率接触器件的基本结构，其形成的致热流场可以作为复杂接触体的研究基础。应用ANSYS的spaceclim模块建立了圆柱固定面电接触模型，采用ICEM模块进行结构离散，应用FLUENT对模型使用有限体积的方法进行计算，分析了不同辐射模型对仿真计算结果的影响。

1.1 模型离散

圆柱固定面接触模型为计算对象，定义为相互贴合的两个圆柱形电接触触头，接触形式为面接触。建立空间直角坐标系，定义面接触的圆心为计算模型原点，圆柱面直径d为特征长度，每个圆柱形电触头高度沿Y轴方向0.2d，上、下2个触头组成的模型厚度为0.4d。定义流体计算域中心为下触头圆柱面圆心，分别沿着Y轴正方向，X、Z轴双向10d的长方体区域。

采用Tetra/Mixed类型进行网格划分，采用Robust（Octree）的网格生成方法。流体计算域区域底面buttom（Y=-0.2d）与下触头直接接触，网格需要划分的更加细致，尺寸限制比全局尺寸限制小，为全局网格尺寸的20%。模型近壁面的边界层网格采用棱柱网格进行局部网格加密处理，如图1边界层网格。计算域网格生成总网格数量69 673，依据行列式和角度准则，进行网格质量分析，分别为0.279 954（行列式最小值），12.646 9（角度最小值），其中小于18（角度）的单元数占比为0.061%，网格质量较好。定义圆柱固定面接触模型壁面为发热源面，温度设置为323.15 K（50℃），计算域壁面为固体壁，温度与环境一致，为300 K（26.85℃）。

图1 边界层网格

1.2 数值计算

分别采用5种辐射模型，包括Monte Carlo辐射模型、P1辐射模型、Rosseland辐射模型、表面辐射（S2S）模型及离散坐标辐射（discrete ordinates, DO）模型，采用k-epsilon湍流模型，近壁面处理为SWF(standard wall functions)，以Coupled为求解方法，进行稳态数值计算，得到了相应的数值计算结果。

不同辐射模型在X=0的截面温度场分布情况，如图2～图6所示。

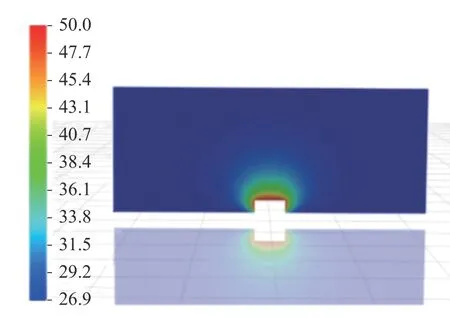
图2 Do辐射模型

图3 P1辐射模型

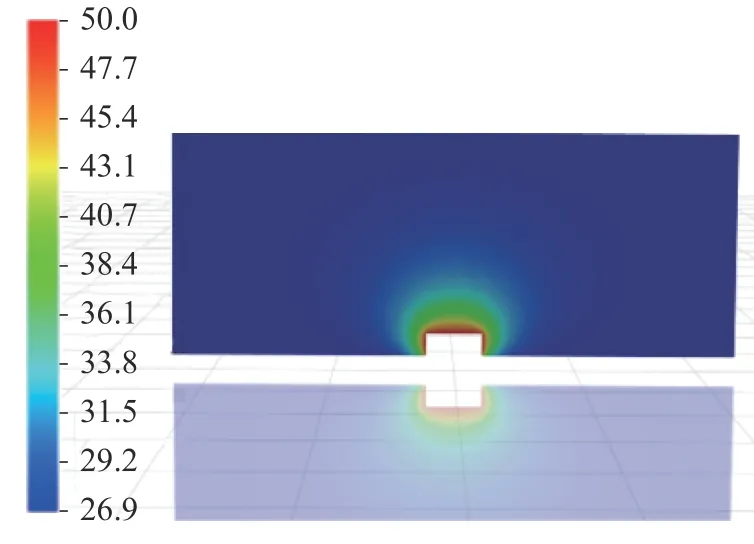
图4 S2S辐射模型

图5 Rosseland辐射模型

图6 Monte Carlo辐射模型

图2～图4所示3种模型获得的温度分布云图，在发热体的上触头顶部温度最高，热量沿着计算域呈发射状向外传递，温度逐渐降低，梯度变化较为平滑。采用Do辐射模型、P1辐射模型、S2S辐射模型均能够较好地计算出模型的致热效应。如图5～图6所示，Rosseland辐射模型与Monte Carlo辐射模型，在有发热热源面的情况下，在局部部位的温度反而降低，甚至低于环境温度，仿真结果与实际情况不符。

分析P1辐射模型、表面辐射（S2S）模型、离散坐标辐射（DO）模型数值计算过程，在能得到较好的仿真结果的前提下，表面辐射（S2S）模型迭代所占用的计算资源较少，是比较理想的模型。

2 封闭体-固定接触模型致热流场计算

接触器是一种常用的带封闭体-电接触结构的大功率电气控制器件，其主要工作部件为不规则外形的接触片，如图7所示。其实时工作电气特性的变化，产生的致热流场在空气流体域中热传递，受封闭体的阻断，在封闭体内、外形成复杂的三维热流场分布，本节在前序模型的基础上，进一步探究CFD仿真方法的有效性。

图7 封闭体接触片

2.1 模型离散

考虑到接触部位的三维结构比较复杂，结构具有非对称性，且存在多种曲面结构，边界上带有加工切角，模型建立过程中需进行针对性处理，如图7所示，非规则接触体结构模型的外形为一个近似的椭圆，带有一个向外延伸的叉状结构及凸出的2个圆柱面接触片，整体为一个对称结构；考虑到边界结构的连续性，避免在网格离散时对网格质量产生影响，特别是四面体网格与壁面的贴合性，造成数值计算结果不易收敛。采用分段细化-平滑的处理方法，定义细化间距为a，取点数量为b，b≥6，使得模型局部特征与实际相吻合，得到了非规则接触体结构模型分段细化-平滑图，如图8所示，进一步生成非规则接触体及封闭体结构模型，如图9所示。

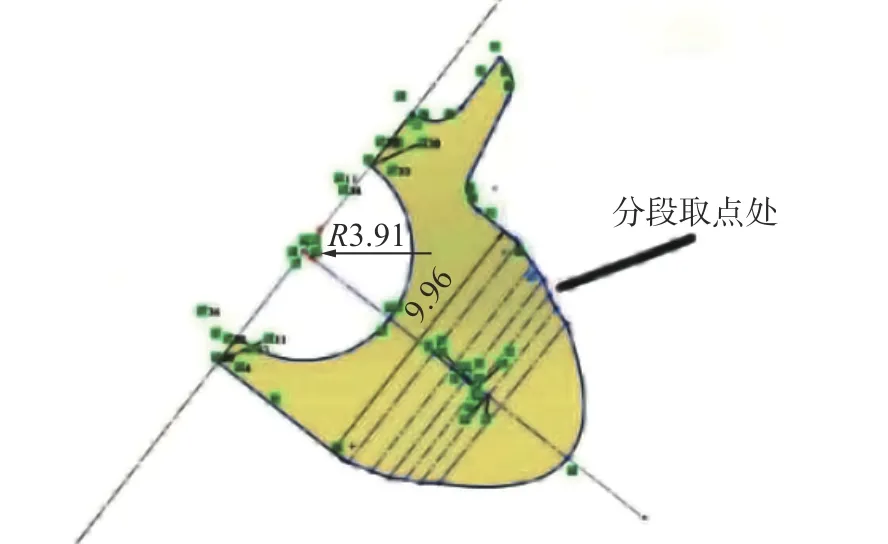
图8 分段细化-平滑处理图

图9 非规则接触体及封闭体结构模型

模型创建中以封闭体几何中心为原点（位于不规则接触片上部），建立空间直角坐标系，Y轴垂直接触面向上，Z轴负方向平行于对称轴，指向叉状结构，在非规则接触体内部生成非结构化网格（定义为固体材质热源）如图10所示。在封闭体内部生成非结构化网格（定义为固体材质），在封闭体和非规则接触体壁面之间创建空气流体域，如图11所示。

图10 模型坐标示意

图11 封闭体网格及空气流体域

计算域网格生成总网格数量140 019，依据行列式和角度准则，进行网格质量分析，分别为0.188 412（行列式最小值），65.692%行列式的值在0.959 302 8 ～0.999 876，9.310 58（角度最小值），其中小于18（角度）的单元数占比为0.01%，网格质量较好，如图12所示。

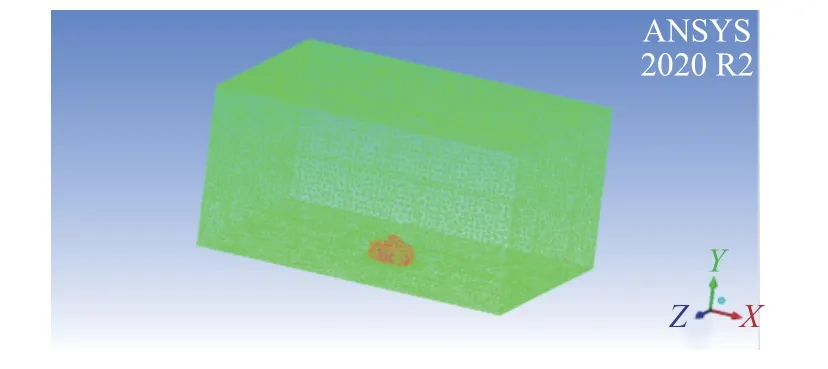
图12 封闭体-固定接触耦合模型流体域网格

在模型求解计算中，启动能量方程，湍流模型选用k-epsilon模型，近壁面处理为SWF。辐射模型采用S2S（表面到表面）模型，完成边界条件设置非金属封闭体及环境温度为12.5℃，接触片温度设置为72.5℃，耦合模式方案为Coupled，初始化流场，进行稳态数值计算，得到了相应的数值计算结果。

2.2 数值计算

针对非规则固定接触体模型进行数值再现，得到温度分布云图，分别垂直于Y、Z、X轴进行切片化处理。当垂直于Y轴进行切片化处理时，分别给出了y=0.976、5.5时切面温度分布云图，如图13和图14所示。2个切面在垂直于Y轴物面上的连贯性和连续性较好，边界结构清晰，形成的温度分布与结构分布相符。

图13 切面温度分布云图

图14 切面温度分布云图

垂直于X轴进行切片化处理，分别给出了x=0、8.11时切面温度分布云图，在非规则接触体靠近接触部位的区域温度相对偏高，如图15和图16所示。

图15 x=0时切面温度分布云图

图16 x= 8.11时切面温度分布云图

2个切面在垂直于X轴物面上也展现了较好的连贯性和连续性，边界结构清晰。当x=0时，在非规则接触体靠近对称的区域，由于叉型结构和安装孔的存在，将该区域分为2个不连续的部分，热阻截面较小，出现了2个独立的温度分布区域，且相对温度偏高；当x=8.11时，靠近非规则接触体的区域温度较高，形成的温度分布与结构分布相符，呈均匀连续的放射状向空间辐射。垂直于Z轴进行切片化处理，给出了z=0和z=-3.963时切面温度分布云图，如图17和图18所示。

图17 z=0时切面温度分布云图

图18 z= -3.963时切面温度分布云图

2个切面在垂直于Z轴物面上依然展现了较好的连贯性和连续性，边界结构清晰。当z=0时，受到非规则接触体触点的影响，出现了2个独立的温度分布区域，且温度分布相对集中偏高；由于中间安装孔区域的热阻较小，两侧的温度呈现一种向中间扩散的趋势。当x=-3.963时，沿结构边界温度分布均匀，应用分段细化-平滑方法取得了较好的效果。

针对封闭体-固定接触耦合模型进行数值再现，得到温度分布云图，分别垂直于Y、Z轴进行切片化处理，并且获取了封闭体表面温度分布图。

当垂直于Y轴进行切片化处理时，分别给出了y=0.005、0.008时切面温度分布云图，如图19和图20所示。

图19 y=0.005切面温度分布云图

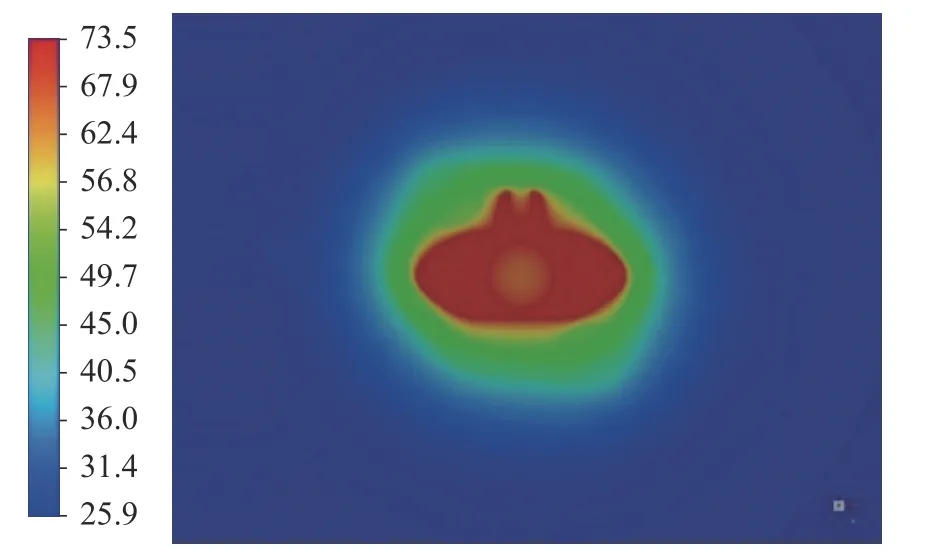
图20 y=0.000 8切面温度分布云图

基于封闭体结构的耦合模型计算出的结果，2个切面在垂直于Y轴物面上的连贯性和连续性较好，有着清晰边界结构。当y=0.005时，因为封闭体顶部具有半球状突起结构，内部为空气域，热阻较低，温度分布集中在此区域，且相对偏高；当y=0.000 8时，靠近非规则接触体温度较高，向外温度逐渐降低，在封闭体处的热阻较高，受到封闭体的影响，温度在封闭体边界处大幅下降，封闭体外部温度下降较为平滑，然后趋向于环境温度，形成的温度分布与实际结构分布相符。

当垂直于Z轴进行切片化处理时，给出了z=0.016 7时切面温度分布云图，如图21所示。当z=0.016 7时，靠近非规则接触体的区域温度较高，形成的温度分布与结构分布相符，呈均匀连续的放射状向空间辐射。

图21 z=0.016 7切面温度分布云图

针对封闭体-固定接触耦合模型进行计算，得出封闭体表面的温度图，得到了明显的温度分布，如图22所示。

图22 封闭体温度分布图

封闭体红外温度图与封闭体上的温度分布云图对比，如图23所示。在封闭体上，高温部分集中在前后两端的圆柱型孔洞处；而侧面，高温部分集中在两侧平台的下部。仿真结果与红外温度分布趋于一致，可以用于计算电接触致热效应。

图23 封闭体红外温度分布图

3 结论

针对在役封闭体电接触，应用分段细化-平滑方法进行结构离散，采用S2S表面辐射模型及kepsilon湍流模型，近壁面处理为SWF，并以Coupled为求解方法，得到的稳态数值计算结果沿结构边界温度分布均匀，在封闭体表面与红外温度谱分布趋于一致，可以用于实际电接触致热效应计算与流场分析。