农村地区无人机配送站点多目标选址优化研究

陈亮，谷晓燕，刘建国，王志钢

(北京信息科技大学 信息管理学院,北京 100192)

0 引言

国家邮政局在《快递进村三年行动方案(2020-2022年)》中明确提出到2022年底符合条件的建制村基本实现村村通快递。无人机物流作为一种全新的物流配送模式，可以有效地提高供应链末端的效率，解决当前供应链末端最后一公里的配送问题[1-2]。合理选择无人机配送站点的数量和位置，是决定无人机配送前期投入和后期运行效率的关键，因此有必要对农村地区的无人机配送站点选址进行研究。

选址问题可以分为最大覆盖问题[3]、集合覆盖问题[4]、P-中值问题[5]和固定费用设施选址问题[6]。面向末端配送领域，肖建华等[7]研究了非等覆盖半径思想下的生鲜农产品配送中心选址问题。毕娅等[8]研究了基于集合覆盖的有容量和时间限制的选址—分配系统的非线性规划模型。王海军等[9]研究了在突发事件背景下时间最小化和成本最小化的双目标应急物流选址—路径随机规划模型。尚猛等[6]研究了配送中心建设成本最小和配送距离最短目标函数下配送中心选址问题。以上这些研究均是针对城市配送或应急物流环境下的配送，针对农村地区配送选址问题也有少量学者开始关注。Pan等[10]提出一种紧凑型的布谷鸟搜索算法用于农村地区无人机物流枢纽的选址，该研究并没有考虑农村地区的地形和无人机的续航里程限制，且配送范围只包括30个村庄。陈刚等[11]构建了军民融合背景下的无人机配送中心选址模型，但是配送目标点只到乡镇级别，而且仅以配送网络总里程最小为目标，用通用软件求解大规模问题的效率也不高。针对大规模问题的求解，启发式算法相比于精确求解算法在求解效率上具有更好的表现，其中禁忌搜索算法和遗传算法被用于求解选址问题。Pramudita等[12]使用禁忌搜索算法求解灾后废物清理站点的选址问题。黄露等[13]对配送中心选址问题应用层次遗传算法进行求解，考虑了顾客的延误损失。但是这些算法都是在小规模给定选址集合中求解出最优的位置，不适用于农村地区可选址区域呈片状连续分布的应用场景。

在无人机配送问题中，大部分文献聚焦于卡车和无人机的联合配送模式，一辆卡车一般携带一架无人机，因此更适用于小规模的配送。本文面向农村地区大规模配送场景，建立最小配送站点数量和最小综合配送距离的双目标选址模型，并结合了贪婪重叠圆算法和改进的萤火虫算法求解该模型，同时考虑无人机续航里程和禁止选址区域对无人机配送站点选址的影响，更加贴合无人机站点选址的实际需求。

1 问题描述与建模

1.1 问题描述

无人机配送站点的运行方式为：将配送站点服务范围内的村庄看作需求点，通过卡车将轻小件货物从配送中心批量运送至各配送站点，无人机配送站点内的多架无人机能够同时依据村庄的需求完成最后的配送。由于卡车和末端配送车辆续航里程较大的原因，常规配送中心的选址未考虑卡车配送的范围，而无人机的配送虽然能够不受地面交通的约束，但是存在着续航里程的限制。对于一个较大的区域，需要同时设置多个无人机配送站点才能为所有村庄提供无人机配送服务。

农村地区多无人机配送站点选址问题可以描述为：在已知农村地区村庄人口、位置以及配送中心位置的情况下，结合农村地区地形和无人机续航里程，在为区域内所有村庄提供无人机配送服务的前提下，寻求无人机配送站点的最优选址方案。优化目标有两个：第一个目标是最小化配送站点数量；第二个目标是最小化综合配送距离，其由配送总里程、配送频次、配送必要程度等因素决定。第一个目标的优先级要高于第二个目标。优先考虑配送站点数量的原因在于，最小的无人机配送站点数量确保了最小化前期固定投资成本。第二个目标中配送总里程与配送成本直接相关，配送总里程越小则成本越低；在长期配送中无人机配送站点离配送频次高的村庄越近则配送成本会越低，这里用村庄的人口数量代替配送频次；同时无人机配送站点还应该离地面交通复杂的村庄近一些，这样更能够体现使用无人机配送的必要性。

1.2 模型假设

1)无人机的配送路径是从配送站点到对应村庄的直线；

2)无人机站点到最远村庄的配送路径长度不大于无人机的续航里程；

3)每个配送站点负责多个村庄的配送服务；

4)每架无人机每次只为一个村庄提供配送服务。

1.3 变量与符号说明

n：村庄的个数；

pi：第i个村庄的人数(i=1,2,…,n)；

k：无人机配送站点的数量；

Gj：第j个无人机配送站点配送村庄的集合(j=1,2,…,k)；

Lj,i：第j个无人机配送站点到第i个村庄无人机配送的距离(j=1,2,…,k；i=1,2,…,n)；

Pj,i：第j个无人机站点到第i个村庄的陆地最短距离(j=1,2,…,k；i=1,2,…,n)；

Hj,i：第j个无人机站点到第i个村庄的相对交通难易程度系数(j=1,2,…,k；i=1,2,…,n)，为Lj,i与Pj,i的比值；

Dj：配送中心到第j个无人机配送站点的最短陆地配送距离(j=1,2,…,k)；

Fj：配送中心到第j个无人机配送站点的配送频次；

w：禁止选址区域的个数；

rm：第m个禁止选址区域的半径(m=1,2,…,w)；

ruav：无人机的续航里程；

(xj,yj)：第j个无人机配送站点的经度和纬度(j=1,2,…,k)；

(ai,bi)：第i个村庄的经度和纬度(i=1,2,…,n)；

(c,g)：配送中心的经度和纬度；

(qm,um)：第m个禁止选址区域中心的经度和纬度(m=1,2,…,w)。

1.4 模型建立

f1=min(k)

(1)

(2)

ruav/2}

(3)

(4)

(5)

(6)

(7)

(8)

目标函数式(1)表示最小化配送站点数量；目标函数式(2)表示最小化综合配送距离，目标函数值越小表示构建的无人机配送站点的选址位置越好；式(3)表示第j个无人机配送站点所服务村庄的坐标集合；式(4)判断村庄i的坐标是否属于第j个配送站点配送的村庄坐标集合，若在集合内则为1，否则为0；式(5)表示每个村庄至少由一个配送站点进行配送；通过式(6)求出配送中心到配送站点的直线距离；通过式(7)求解无人机配送站点到村庄的距离；式(8)表示无人机配送站点必须位于禁止选址区域外。

2 算法设计

由于两个目标存在着不同的优先级，本文采用分层序列法依次求解每个目标。通过引用贪婪重叠圆算法确定无人机配送站点的最小数量，然后运用改进的萤火虫搜索算法求出综合配送距离最小条件下的无人机配送站点位置。

2.1 无人机配送站点最小数量求解

贪婪重叠圆算法通过确定固定半径大小的圆的最小数量，来实现对区域内节点的覆盖。以无人机配送站点为圆心，其配送范围近似为一个圆。因此，本文基于贪婪重叠圆算法[14]来确定无人机配送站点的最小数量。以所有村庄坐标集合中的经度最小值和纬度最小值作为坐标原点，算法步骤如下：

1)根据所有村庄和原点间的距离，按照升序依次对其进行编号，并存入村庄集合Q中；

2)令i=1；

3)找出Q中编号最小的村庄，并将该村庄作为第i个中心节点Oi；

4)找出距离Oi不大于ruav的村庄，该覆盖圆命名为第i特征圆；

5)再将这些村庄加入候选集合，然后从总节点集合Q中移除；

6)在第i特征圆范围内确定出一个或多个配送站点的位置；

7)令i=i+1，重复执行3)至5)，直到Q=∅。输出圆的数量和圆心位置，作为配送站点的数量和初始位置。

2.2 无人机配送站点位置求解

在第一阶段，确定了无人机配送站点的最小数量及初始位置，但此时的站点位置并不是最优解，本文使用改进的萤火虫算法来求解配送站点的最优位置。为了不缩小解的空间，将从全局对无人机配送站点的位置进行确定。常规萤火虫算法有着搜索速度慢、易陷入局部最优的问题，因此，本文对传统萤火虫算法做出了两方面的改进：第一是设置线性惩罚项，相比于单一的惩罚项，线性惩罚项能够依据超出无人机配送范围外村庄的数量，来施以不同程度的惩罚，加快萤火虫向最优位置的迭代；第二是设计了一种反向自我扩散学习机制，当检测到陷入局部最优时，能够自适应地调整萤火虫移动步长因子，帮助萤火虫跳出局部最优。

2.2.1 萤火虫基本算法

萤火虫算法(firefly algorithm，FA)是一种模拟萤火虫之间相互吸引的算法[15]，不同萤火虫之间的荧光度存在着差异，萤火虫会向着更亮的萤火虫移动，以此来完成迭代寻优。由于本文研究的是多个配送站点的选址问题，且配送站点的位置关系对解存在影响，因此每个萤火虫代表无人机配送站点选址问题的一个候选解。萤火虫通过适应度值来决定其荧光亮度：适应度值大的萤火虫亮度大，吸引力大；适应度值小的萤火虫亮度小，吸引力小。萤火虫基于个体之间的相互吸引，使亮度小的萤火虫向亮度大的萤火虫移动，进行解的搜索。

针对无人机配送站点选址，FA基本算法描述为：

1)不同的无人机配送站点选址的各候选解，即萤火虫之间，相对亮度为

I=I0×e-γrij

(9)

式中：I0为最大荧光亮度；γ为光吸收强度；rij为萤火虫i与萤火虫j的空间距离。

2)萤火虫i与萤火虫j的相对吸引度为

(10)

式中β0为最大吸引度。

3)萤火虫i被萤火虫j吸引后，通过式(11)进行位置更新，Vi表示第i个萤火虫的空间位置：

(11)

式中：α∈[0,1]为步长因子，调节步长因子的大小即可实现萤火虫在全局和局部搜索的能力；R为[0,1]上均匀分布的随机数。

2.2.2 线性惩罚项

在算法初始迭代过程中，由于初始选址位置具有一定的随机性，会出现村庄位于无人机配送范围外的情况，如果添加一个单一的惩罚值，若首次迭代时无可行解，则会造成萤火虫因为目标函数值都偏小，无法向可行解移动的问题。因此本文依据超出无人机配送范围村庄的数量不同，来设置不同大小的惩罚值，有利于配送站点的位置逐步向未覆盖村庄数量少的位置进行逐步移动，进而达到全部覆盖的目的。设惩罚因子为ε，则线性惩罚项为

(12)

对应的适应度函数设为

(13)

2.2.3 反向扩散学习机制

当前萤火虫算法的步长因子多为一种单调递减的自适应函数，即在前期步长因子较大，从而完成较大区域的搜索，后期步长因子变小完成局部搜索。由于其他萤火虫都向最亮的萤火虫聚集，在算法中期或者后期萤火虫所代表的配送站点位置都不可避免地聚集在一起，配送站点之间的距离就会非常小，因此式(10)中吸引度趋近于0。而由于步长因子一般为自适应的单调递减的函数，在迭代后期步长因子会变得非常小，搜索区域逐步变小，从而难以跳出局部最优。

为了加速找到最优解，本文在判定目标函数在一定次数内未更新时，就会更新自适应步长因子，增大其搜索范围，通过连续执行多次寻优，尽可能地找到更优的解。由于此时反向扩散学习机制只有一个萤火虫，没有种群的思想，为了不增大算法的运行复杂度，算法每执行一次反向扩散学习机制，则通过式(14)相应减少最大迭代次数，式中M为最大迭代次数，N为反向扩散学习迭代次数，P为种群数量。

M=M-N/P

(14)

由于一个萤火虫代表着k个配送站点的位置，即V={v1,v2,…,vk}，vi为第i个配送站点的位置。一个萤火虫位置的移动一般会使得多个配送站点的位置同时发生移动，为了方便寻找到更优的位置，在自我扩散学习机制中每次将会随机挑选一个站点的位置进行寻优，学习机制如式(15)所示。

vi=vi+α(R-0.5)

(15)

通过对比和测试，设置步长因子自适应函数[16]，如式(16)所示。

α(t+1)=α(t)×e-30×(t/M)2+αmin

(16)

式中：αmin为最小自适应步长因子；t为迭代次数。在执行反向扩散学习机制时，M变为对应的反向学习机制的最大迭代次数，t重新从1开始进行迭代。

2.2.4 改进萤火虫算法步骤

1) 初始化参数：种群数量P、最大迭代次数M、移动步长因子α、最小移动步长因子αmin，目标函数未更新次数l=0，迭代次数t=0；

2) 初始化P个萤火虫的位置，并将第一阶段输出的k个配送站点的位置作为第一个萤火虫的位置；

3)每个萤火虫中包含k个配送站点的位置，依据各村庄到这些站点的最短距离，将所有村庄分为k个簇，设定惩罚因子大小，通过式(12)计算线性惩罚项的值，然后通过式(13)计算适应度值作为萤火虫的亮度；

4) 通过式(10)计算萤火虫之间的吸引度进行光吸收系数调整，并通过式(16)更新步长因子；

5)通过式(11)更新萤火虫的位置，并与上一次的最优解进行对比，如果最优解没有减小，则令l=l+1；

6)判断l是否大于最大设定的未更新次数，如果大于则进行反向扩散学习；

7)令t=t+1，若t=M则输出最终结果，否则返回3)。

3 算例分析

本文选取湖北省孝感市大悟县作为研究区域，大悟县属于丘陵地区，受地形限制，部分村庄与村庄的地面交通距离要远大于直线距离。以大悟县所属村庄的人口数量以及位置分布作为基础数据。通过百度地图开放平台标注村庄位置，如图1所示。将4座山峰设置为禁止选址区域，禁止选址区域具体数据如表1所示。依据丘陵地形特点将相对交通难易程度系数假设为0.5。根据国内迅蚁最新一代多旋翼无人机RA3的最大续航里程，本文将无人机的最大续航里程设为20 km，即能够完成半径10 km内的所有村庄的配送。配送中心到各配送站点的配送频次系数设为10。

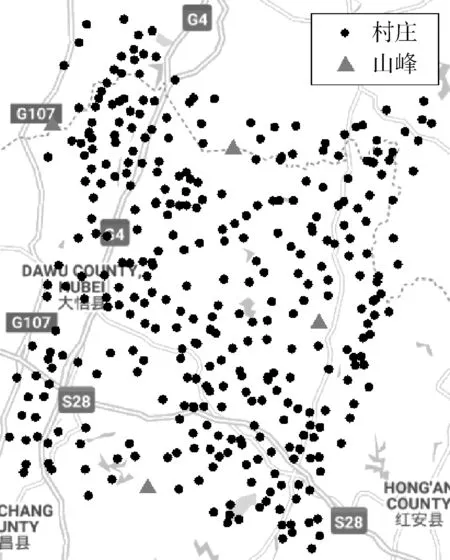
图1 村庄分布卫星图

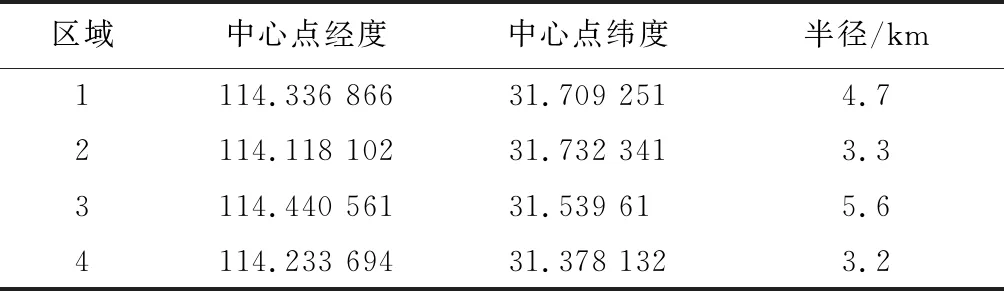
表1 禁止选址区域数据

3.1 选址结果

通过本文算法对算例进行求解，选址结果为：共需设置4个配送站点就能为所有村庄提供无人机配送服务，使用改进萤火虫算法求解的最小目标函数值为42 159.5。配送站点的位置及配送区域如图2和图3所示。

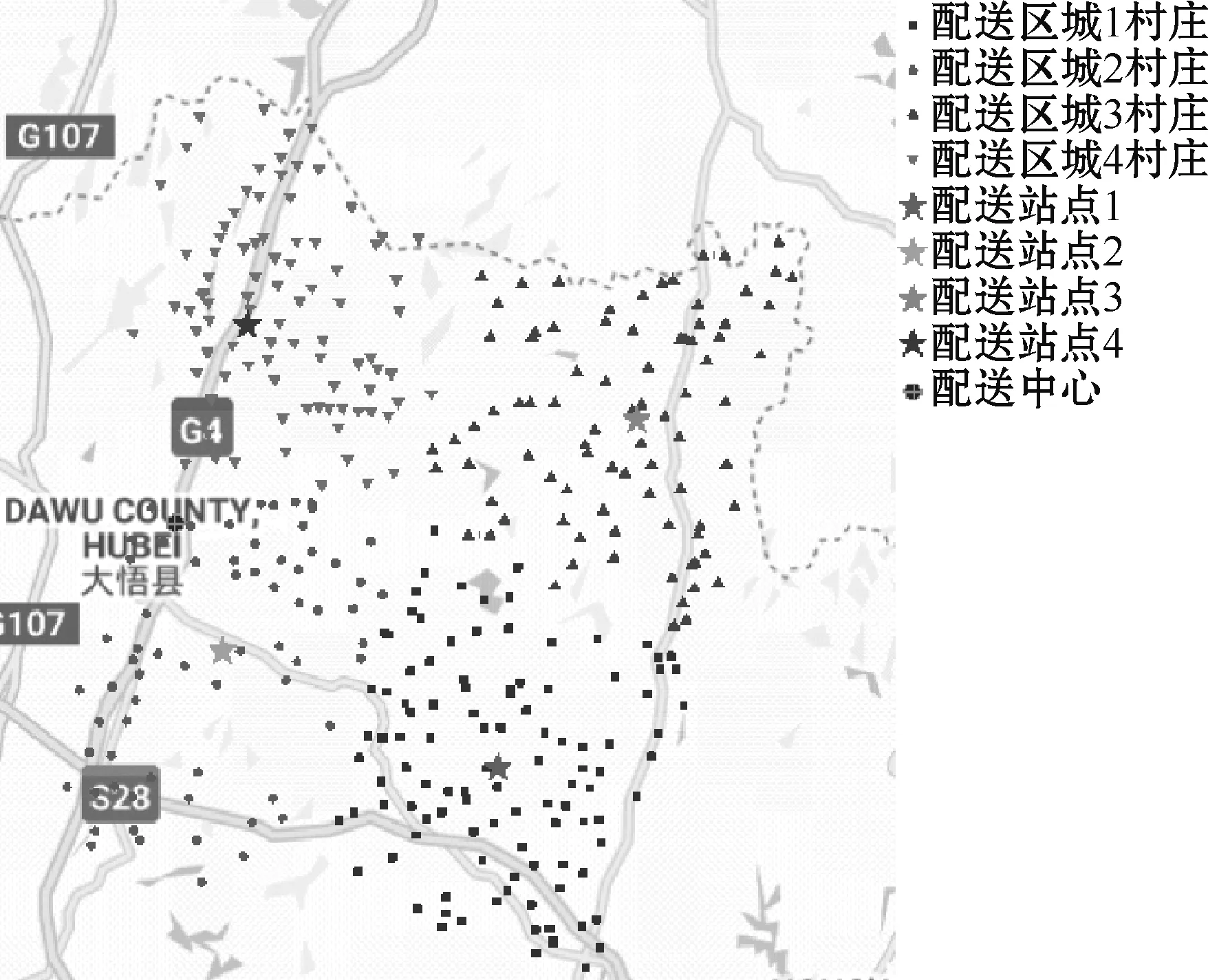
图2 配送站点及配送区域卫星图

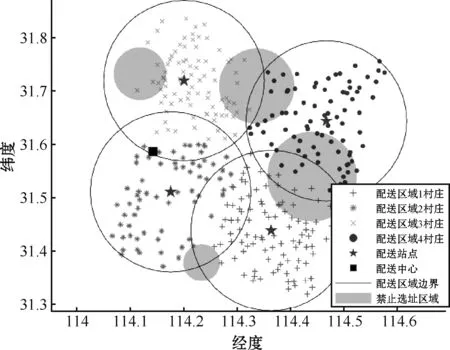
图3 配送站点及配送区域散点示意图

3.2 反向扩散学习机制的有效性验证

为了验证本文的反向扩散学习机制的搜索效果，对普通萤火虫算法添加线性惩罚项，设置相同的自适应步长函数，并设定配送站点数量为4，与本文算法对比，分别连续运行100次，每次的迭代次数设为500。两种算法的求解结果如图4所示。

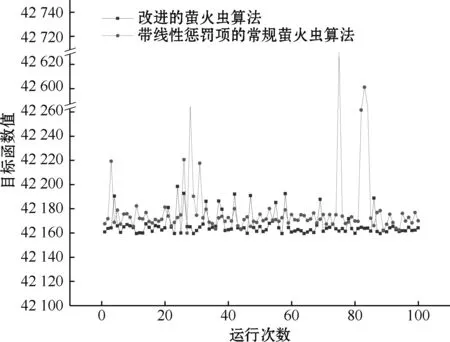
图4 算法求解结果对比

从图4可以看出，改进的萤火虫算法的求解效果要明显优于只带惩罚项的萤火虫算法。本文算法的均值为42 166.6，最大最小值差值为38.98，标准差为9.02。而只带惩罚项的萤火虫算法的均值为42 186.7，最大最小值差值为502.38，标准差为69.62。改进的萤火虫算法的均值要低于只带惩罚项的萤火虫算法，标准差要减小87.04%，稳定性更好，验证了反向扩散学习机制的有效性。

3.3 算法寻优能力对比

为了探究改进萤火虫算法(improved firefly algorithm，IFA)的寻优能力，将其与现有成熟的典型群智能算法进行比较，选取了粒子群算法(particle swarm algorithm，PSO)、差分进化算法(differential evolution algorithm，DE)以及常规萤火虫算法(FA)作为参照算法，并对以上算法均设置线性惩罚项，惩罚因子设为5 000。另外为了对比线性惩罚项和单一惩罚项的区别，对常规萤火虫算法另外设置了单一惩罚项，称为带单一惩罚项的萤火虫算法(firefly algorithm with a single penalty，FA_SP)。5种算法参数设置如表2所示，迭代次数设为500，迭代过程的对比结果如图5所示。

表2 各算法参数设置

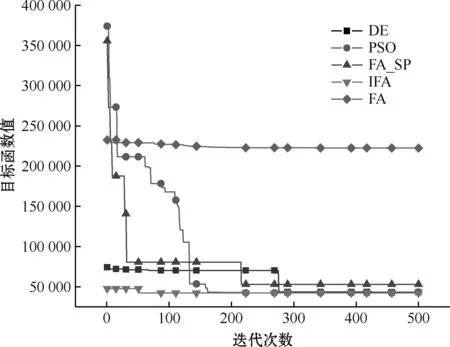
图5 五种算法迭代过程对比

由于改进的萤火虫算法利用了第一阶段的贪婪重叠圆算法的圆心，拥有了一个质量较高的初始解，其初始目标值会小一些。差分进化算法虽然在一开始也能寻找到较好的一个初始解，但是在后期仍需要较多的迭代次数才能跳出局部最优，而IFA算法能够更快跳出局部最优寻找到最优值。设置单一惩罚项的萤火虫算法，迭代效果要明显不如另外几种算法。由图5可知，5种算法最终都能找到最优解或者接近最优解的位置，但是改进的萤火虫算法能够在更短的迭代次数内找到更好的解。

4 结束语

本文针对无人机配送站点选址问题进行了研究，提出了一种无人机配送站点选址算法，为验证模型和算法的有效性和实用性，选取了湖北省的一个县作为算例进行对比分析。结果表明：1)本文所提出的选址模型能够确定为所有村庄提供无人机配送服务所需无人机配送站点的最小数量，以及配送站点的最优位置；2)本文所提出的算法能够快速有效地求解模型，可以为物流企业面向农村地区无人机配送网络布局提供决策。面对用户的个性化需求，未来研究可以从考虑村庄需求不确定性、时间窗约束和无人机单航程多点配送的路径规划等方面展开。