解决数学问题——《4.2 数值计算》（第一课时）教学设计

许月媚 广东省广州市南武中学

数学是计算机科学的理论基础之一，计算机技术的出现和发展最初源于数学问题求解。由于自然科学领域需要进行大量的数值计算，而人工计算又存在效率落后、精确度低等不足，往往无法满足计算要求，因此，就需要借助计算机程序来弥补人工计算的不足，同时解决很多数学方法所描绘的数值计算问题。

● 学习内容分析

本课节选自2019年教科版《必修1 数据与计算》第4单元“计算与问题解决”第2节《数值计算》，旨在帮助学生在了解算法及其特征的基础上，学会分析问题，运用数值类问题求解的常用算法——解析法来解决实际问题。本课为《数值计算》的第一课时，重在实现学科知识的融通，将数学函数解析式求解与计算机模拟相融合，突出计算机在解决问题过程中的地位和作用。通过“解决数学问题”案例活动，引导学生体验和探讨计算机解决问题的过程。

● 学习者分析

本课的学习对象为高一年级的学生，他们虽然在数学、物理课上经常运用解析法解决问题，但很少能够主动利用计算机程序实现问题求解。经过第2单元“编程计算”的学习，学生基本具备本节案例学习的知识储备——程序设计的三大结构、输入输出函数、列表、自定义函数、模块等，但考虑到大多数学生对程序设计知识的遗忘率较高，在教学过程中有必要对相关知识进行巩固，以提高课堂教学的有效性。

● 学习目标

①了解解析法的概念以及计算机绘制函数图像的基本原理。②掌握计算机编程解决问题的一般过程，能够根据实际问题来抽象问题特征、建立结构模型、合理组织数据、设计算法方案，进而掌握Python绘制图像的基本方法。③通过数学问题的求解，逐步理解计算机进行数值计算的基本流程和方法，并能够将其迁移至学习和生活场景中的其他问题解决过程中。

● 教学过程

1.导入新课，提出问题

学习目标：①设计解析式进行数值计算、解决实际问题；②感受数据的图形化表示；③了解解析算法在实际问题解决过程中的应用。

导入：计算机的最初用途是用于数值计算，它运算速度快，精确度高，借助它可以解决许多数学问题。

提出问题：如何选择最优化草莓支付方案？某草莓采摘园在春节期间推出了甲、乙两种优惠方案，优惠前的草莓定价为50元/kg。甲种优惠方案：游客进园需要购买40元的门票（每个家庭购买一张门票），采摘的草莓均按定价的六折卖给采摘游客。乙种优惠方案：游客进园不需购买门票，采摘的草莓按定价出售，但超过3kg后，超过的部分按定价的五折卖给采摘的游客。问题一：采摘8kg草莓，选择哪个方案更优惠？问题二：采摘重量在什么范围时，游客选用甲种优惠方案更合算？

设计意图：让学生明确本节课的学习主题，了解学习目标及内容。

2.问题一求解，分析问题

问题一求解：已知采摘重量求费用——采摘8kg草莓，选择哪个方案更优惠？

思考1布置：请用数学方法求解该问题。假设采摘草莓的重量为x（kg），甲种优惠方案采摘所需的总费用为y1（元），乙种优惠方案采摘所需的总费用为y2（元），列出y1、y2关于x的函数关系式。

设计意图：引导学生思考、设想，调动学生已有的知识储备，对问题进行分析，通过数学方法解决问题一。

3.问题一求解，解决问题

提问：采摘重量不定，如何快速选择费用方案？

编程解决问题：尝试用计算机编程去解决，设计费用计算器。通过流程图表示计算器的功能设计（如图1），结合数学方法来设计解决问题的算法。

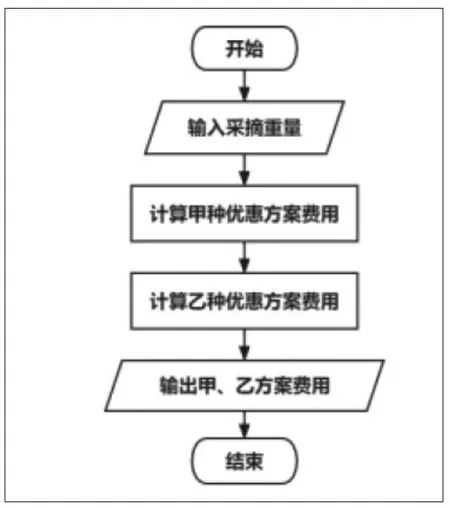
图1 流程图

提问：我们知道甲种方案是一个分段函数，分段函数在编程中如何实现？

讲解：复习自定义函数；讲解分段函数关键代码。

任务1布置：用解析法设计费用计算器——打开图2的Python程序文件，补充并调试运行程序。

图2 Python程序文件

任务1参考答案：①float；②50*0.6*x+40；③0＜=x＜=3；④y=25*x+75；⑤f(x)。

讲解：①计算机编程解决问题的一般流程（如图3）。②解析法：用解析的方法提出问题条件与结果之间关系的数学表达式，并通过表达式的计算来实现问题求解。

图3 计算机编程解决问题的一般流程

小结：基于解析法的问题解决流程（如图4）。

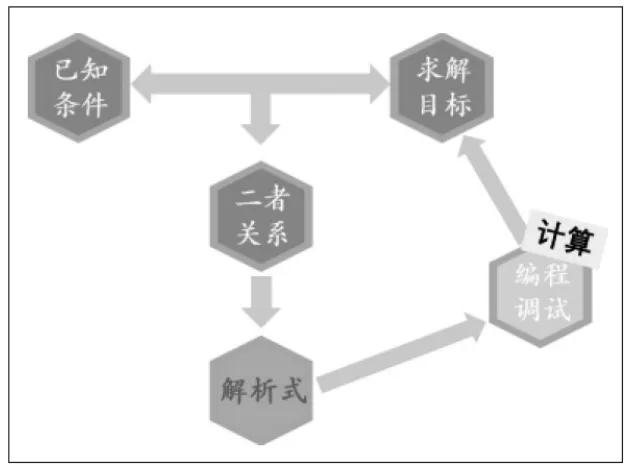
图4 基于解析法的问题解决流程

设计意图：针对问题一的求解过程，分析问题环节已完成数学方法解决问题的基础铺垫，此部分旨在让学生完成费用计算器的程序编写，实现计算机编程解决问题。通过问题引导，让学生以填空的形式编写程序，降低难度，能够消除学生的畏难情绪；通过数学问题的求解，帮助学生理解解析法的概念与应用，着重培养学生的计算思维能力，实现知识建构。

4.问题二求解，分析问题

问题二求解：比较不同的优惠方案——采摘重量在什么范围时，游客选用甲种优惠方案采摘更合算？

思考2布置：数学上有哪些解决该问题的方法？请选择其中一种并作简单描述。

解决问题的方法：①比较法，通过计算解析式得出结果；②列表法，通过计算能得到选定的x，y数值；③图像法，绘制函数图像，观察图像。

设计意图：学生思考，对问题进行分析，通过数学方法解决问题二。

5.问题二求解，解决问题

提问：用哪种方法更适合快速找到区间范围？数学上如何绘制函数图像？

讲解：①图像法绘图步骤：列表—描点—连线。②计算机编程绘制函数图像与数学方法绘制函数图像相似：使用numpy模块列表（numpy模块讲解）；使用matplotlib模块描点、连线（matplotlib模块讲解）。

任务2布置：编程绘制图像——打开如图5所示的Python程序文件，补充并调试运行程序。

图5 Python程序文件

设计意图：对比解决同一问题的不同方法，可以让学生感受不同问题解决方法的差异，并学会选择效率高、效果好的方法。对于问题二求解，图像法更适合快速找到区间范围。数学绘制函数图像的步骤能够促进学生理解计算机编程绘图的步骤，让学生理解Python在程序设计中的优势，激发学习的热情。

任务2参考答案：①f(i)；②np.arange；③50*0.6*x1+40；④plt.plot；⑤plt.show。

6.知识巩固，目标达成

知识小测：

（1）计算圆面积的算法描述如下：①输入圆的半径r，②计算圆的面积s=pi*r**2，③输出圆的面积s，④结束。这个算法是属于（ ）？（单选题）

A.枚举法 B.解析法 C.二分法 D.迭代法

（2）人们对计算机的最初应用大多是数值计算，主要借助计算机运算速度快、精确度高的特点来解决各种数学问题，如（ ）等都属于数值计算。（多选题）

A.函数的计算 B.方程的求解C.数列求和 D.二分查找

（3）尝试用Python绘制y=x^2-2x+1的图像（如图6）。（完善程序）

图6 Python绘制y=x^2-2x+1的图像

设计意图：知识巩固，检查目标达成情况。

知识小测参考答案：（1）B。（2）ABC。（3）①import；②arange；③plot；④show。

7.总结归纳，知识建构

引导学生归纳、总结、梳理本节课的学习内容，进行知识提炼，实现知识建构，并能够将利用信息技术解决问题的过程迁移到学习和生活场景中的其他问题解决过程中。

● 教学反思

本节课采用“提出问题——分析问题——解决问题——目标达成——知识建构”的教学模式，以学生熟悉的数学问题作为活动主线，通过典型、针对性强的生活案例，将相关基本概念、解题方法和思路传授给学生。

教材第2单元已提及计算机解决问题的本质，即分析解决问题的方法和步骤，用计算机能够识别的方式表示信息，使其成为计算机能够处理的数据。以新课标为依据，活用教材，本教学设计围绕“设计费用计算器”和“绘制函数图像”两个任务来开展教学，在任务一“设计费用计算器”中，可借助学案导学，引导学生从数学求解入手，启发思维，让学生逐步形成使用自然语言或流程图描述算法的思路。任务一的核心是研究合理的数学模型和求解算法，任务二“绘制函数图像”是任务一的延伸，难度也有所增加，程序中numpy模块和matplotlib模块的加入以及自定义函数的运用需要教师做好讲解。在教学中笔者也发现，阶梯式的任务设计有助于激发学生学习的积极性和求知欲，采用数学函数解析式求解与计算机模拟相融合的方式，有利于培养学生的信息意识，并在探究实践、验证及解决问题的过程中促进学生的知识迁移，发展学生的计算思维。