基于GSTCs方法的超表面特性研究
穆 迪,王海江
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引言
超材料作为一种新型材料,通常是由整个空间区域内按一定规则排布的散射体或小孔阵列构成,能够设计出多种天然电磁材料无法实现的电磁特性,包括负折射率、零折射率等。超表面是超材料的表面部分,是一种厚度远小于波长的超薄层结构,在研究中常将其近似为二维材料进行处理。与具有一定厚度的超材料相比,超表面占据更少的物理空间,同时对电磁波造成更小的损耗。
由于超材料的体积、重量、损耗等因素的影响,以及其本身在制造工艺上的难度,在频率范围和功能扩展性上的制约,使得超表面逐步取代了传统超材料的地位。近年来,超表面在各个邻域都有着广泛的应用,比如可控智能超表面、空腔谐振器、新型波导结构、吸波器、生物医学设备等。
为了模拟电磁波在超材料中的传播过程,进而设计超材料的结构参数实现预期的调制功能,目前针对超材料的主要分析方法有等效电路法、广义斯涅尔定律法、等效阻抗法等。针对超表面的结构特征,研究人员利用边界条件对超表面处的电磁特性进行数值分析。其中广义薄层转换条件GSTCs是近年兴起的一种高效的超表面分析数值方法,用极化率张量表示超表面的结构特征,从数值角度分析超表面对入射电磁波的作用,进一步设计超表面的参数实现特定的调制功能。
1 GSTCs基本原理
GSTCs是一种应用于超薄层结构处(电磁场的边界条件)分析的方法。基于狄拉克分布的导数展开形式来表征超薄层结构两侧的不连续性,利用极化率来表示超薄层的结构、电磁参数,从而将“微观”的结构与宏观的极化率联系起来,用等效的方法来描述超薄层的整体电磁特性,其分析模型如图1所示。

图1 GTSCs分析模型
为了将微观结构与宏观量联系起来,可以将电场和磁场用电极化密度和磁极化密度表示,根据参考文献[8]中的公式推导,假设超表面置于=0处,可以得到:
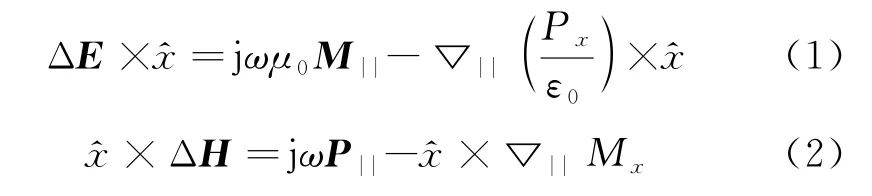
式中:下标||表示平行于超表面方向的分量。
可以看出,常规求解包含了矢量散度的计算,会导致方程的求解量异常庞大,因此在实际应用时,通常假设法相极化密度为零,即P=M=0,再代入极化密度与场值的关系,可得:

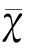
将电场和磁场分别用分量的形式表示,有:

超表面的主要功能是对入射电磁波进行调制,实现对反射、透射波的幅度、相位、传播方向的控制,图2给出了GSTCs方法在超表面整体设计中的4个步骤。

图2 超表面整体设计
其中过程①是根据超表面等效的极化率张量求解边界条件;过程②是根据确定的超表面结构,推导其等效的极化率张量;过程③依照确定的极化率取值,反推相应的超表面结构参数和电磁参数;过程④是从具体的调制功能出发,求解欲实现该功能所需的极化率取值。文章针对步骤①和④进行分析,推导时域有限差分(FDTD)下的GSTCs方法的方程,并给出仿真实例验证分析和公式推导的正确性。
2 基于GSTCs方法的FDTD 方程
为了模拟电磁波入射超表面的传播过程,将GSTCs方法与数值算法结合。文章中将GSTCs方法引入FDTD 算法中,具有以下的优势:(1)仅需变换超表面相邻网格处电磁场方程,计算效率高;(2)与一般FDTD 算法相比,超表面处的方程仅与极化率相关,算法易实现;(3)不同极化率取值可以模拟不同超表面,通用性高。为了验证FDTD 算法实现GSTCs方法的正确性,分别对一维和二维超表面进行方程推导和仿真验证。
2.1 一维超表面
假设超表面置于平面处,如图3所示。在不考虑法相分量的情况下,电场和磁场同时有和两方向的分量,为简化运算,同时保证方程有唯一确定的解,极化率仅需保留4个量描述边界处电场和磁场的数值关系,此时式(5)可以表示成4阶对角矩阵:

图3 二维GSTC-FDTD 节点分布
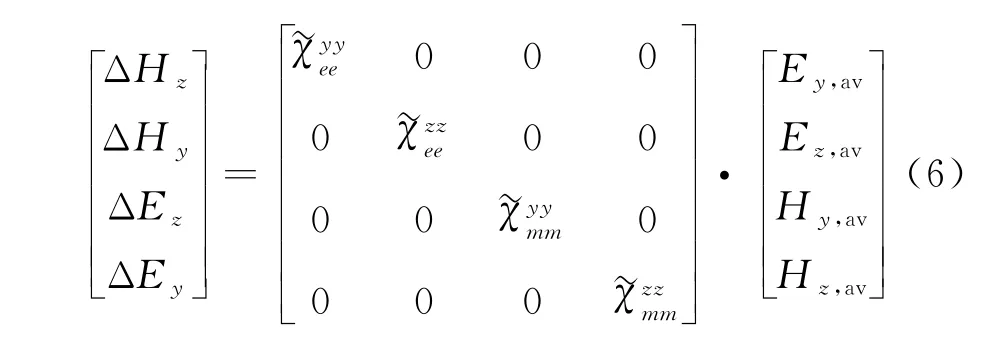
将式(6)代入到式(5)中,有:
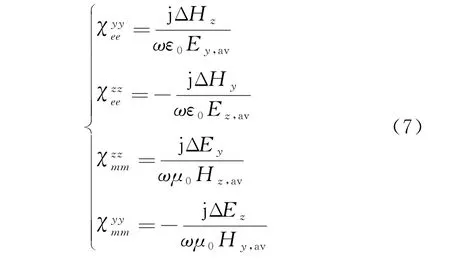
以电场分量为例,迭代方程的一般形式为:

超表面处以0+处的磁场代替处的磁场,这样方程中的各分量均处于超表面同侧,可以采用一般形式的FDTD 方程,有:
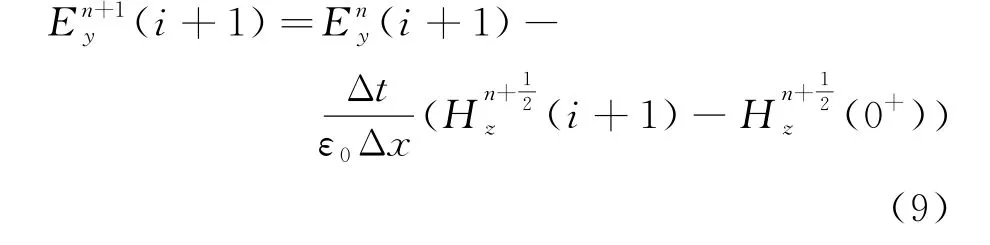
由式(7)可得,超表面处的边界条件为:
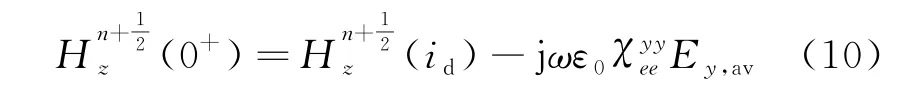
将式(9)代入到式(8)中可以得到超表面处电场分量的迭代方程:

同理可得电场分量以及磁场的方程。
2.2 二维超表面
图4给出了二维超表面处的节点分布,其中超表面置于平面上。以TM 波为例,由于不考虑法相分量的作用,磁场分量不需特殊化处理,因此,单模式调制的方程为:

图4 二维GSTC-FDTD 节点分布
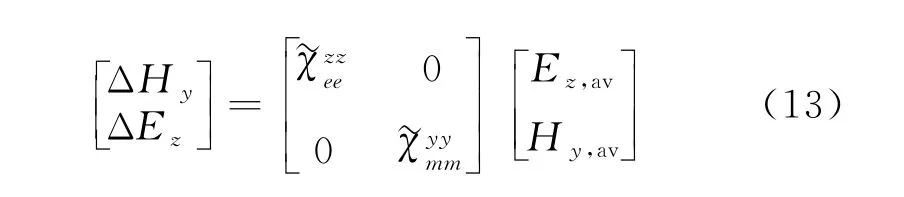
对照一维的思路可以推导出超表面处迭代方程。二维超表面的双模式调制,就是假定副对角线上的极化率不为0时的超表面功能。此时的方程形式可以表示成:

可以看出,此时的超表面可以对入射电磁波实现2种不同的调制功能。
3 仿真结果
3.1 一维幅度、偏转角调制
一维超表面能够对入射电磁波的反射波和透射波的幅度、偏转角进行调制,仅需找到幅度、偏转角与超表面极化率的对应关系即可模拟电磁波入射超表面时相应的调制功能。
进行方程推导时分别研究了对入射电磁波的幅度、偏转角的调制功能,进而推导出幅度、偏转角同时调制的电磁方程。图5给出了一维超表面幅度和偏转角同时调制时电场和磁场的空间分布,其中薄板表示超表面的空间位置。入射电磁波是幅度为1、偏转角为45°的正弦波,预设的调制功能为:反射系数=0.25,透射系数=0.5,投射偏转角为75°。

图5 一维幅度、偏转角同时调制
为了从数值角度研究调制效果,给出幅度与偏转角的分布曲线,如图6、图7所示。
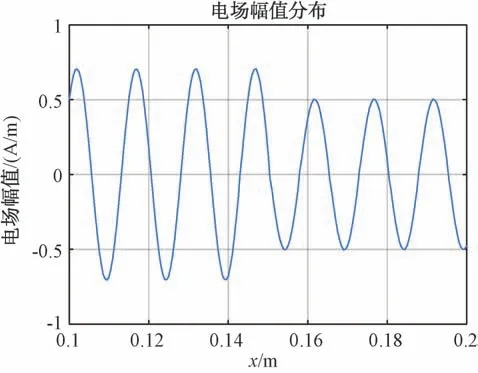
图6 一维调制幅度分布
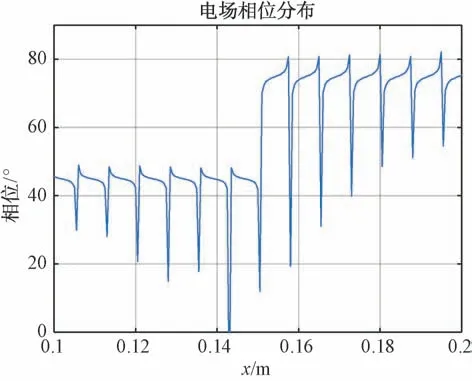
图7 一维调制偏转角分布
可以看出,由于仿真时计算网格粗细等因素的影响,局部数值存在差异,但幅度和偏转角曲线的整体趋势与预设的调制功能相符。
3.2 二维幅度调制
由于二维算法只与电场、磁场单个方向分量相关,因此算法仅能够对入射电磁场的幅度进行调制。
首先研究部分透射。此时预设超表面对入射电磁波无反射,且透射系数为0.5,仿真结果如图8、图9所示。
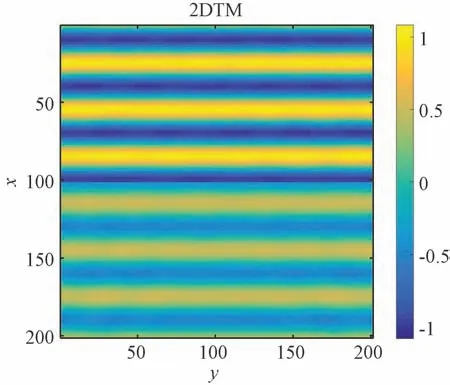
图8 R=0,T=0.5场分布
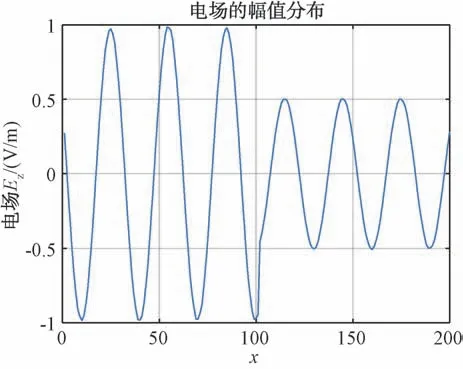
图9 R=0,T=0.5幅度分布
图8、图9中分别给出了正弦波垂直入射时场分布图和=100平面处的幅度分布曲线,可以看出垂直入射时幅度调制效果与预设的功能吻合得很好。
为了验证二维算法的通用性,研究反射系数、透射系数都不为零时,45°斜入射电磁波在超表面处的电场变化。此时预设的反射系数为=0.25,透射系数=0.25,实现对反射波和透射波幅度调控的功能。
图10和图11 分别给出了场值分布图和=100时的幅度分布曲线,从图10、图11中可以看出,超表面两侧幅度变化和场值分布符合预设的调制功能。

图10 R=0.25,T=0.25场分布

图11 R=0.25,T=0.25幅度分布
综合一维和二维的仿真结果可以看出,通过预设的调制功能求得的极化率,在仿真电磁波入射超表面时,能够准确地实现预设的调制功能,因此GSTCs方法可以有效地应用到超表面功能设计中。
4 结束语
GSTCs方法的核心思想是用极化率来代替超表面的电磁、结构参数,进而有效、便捷地对超表面进行功能设计。
目前已有研究人员在对从超表面结构计算极化率的过程进行研究。未来GSTCs方法的研究,需在此基础上总结超表面电磁参数、结构参数与极化率的数值关系,建立模型库,将典型的超材料表面结构模型与极化率一一对应,从而对预设调制功能求解极化率数值,进一步从模型库和结构与极化率的对应关系中找出相应的结构模型,实现从预设功能到超表面的设计。

