带不同时滞的单通道ARMA信号加权融合反卷积Wiener滤波器

孙赫 王稳稳 周国振 程婵娟 封文清

摘  要：对带不同的时滞、不同的有色观测噪声和白噪声的ARMA信号，文章根据模型转换算法，推导出相应的反卷积Wiener滤波器，通过计算互协方差阵得到加权阵，采用标量加权得到单通道ARMA信号的最优标量加权融合反卷积Wiener滤波器。通过仿真例子说明，按标量加权融合算法的精度高于每个局部滤波器的精度，验证了算法的正确性。

关键词：多传感器信息融合;时滞;有色噪声;反卷积Wiener滤波方法

中图分类号：TN713       文献标识码：A文章编号：2096-4706（2022）03-0054-04

Weighted Fusion Deconvolution Wiener Filter for Single-Channel ARMA Signal with Different Time-Delays

SUN He1， WANG Wenwen1， ZHOU Guozhen1， CHENG Chanjuan1， FENG Wenqing2

（1. Nanjing Paneng Electric Power Technology Development Co.， Ltd.， Nanjing  210032， China; 2.School of Information and Control Engineering， China University of Mining and Technology， Xuzhou  221116， China）

Abstract： For ARMA signals with different time-delays， different colored observation noise and white noise， according to the model conversion algorithm， this paper deduces the corresponding deconvolution Wiener filter， The weighted matrix is obtained by calculating the cross covariance matrix， and the optimal scalar weighted fusion deconvolution Wiener filter of single channel ARMA signal is obtained by scalar weighting. Simulation examples illustrate that the accuracy of scalar-weighted fusion algorithm is higher than that of each local filter， which verifies the correctness of the algorithm.

Keywords： multi-sensor information fusion; time-delays; colored noise; deconvolution Wiener filtering method

0  引  言

在工程實际中带传感器或检测仪表的系统中，常常存在被噪声污染的观测信号，这是由于传感器和检测仪表带有一定的测量噪声（即测量随机误差），另一方面在检测过程中还可能受到其他噪声干扰。随着电子计算机、军事、计算机技术、信号检测与处理技术、控制技术和空间技术的快速发展，数据量变得越来越庞大，实际系统变得越来越复杂，带噪声的单传感器系统已经不能满足要求，在此基础上，为了要达到及时、准确、高精度和最优的反卷积滤波器，出现大量的多传感器系统，并由此发展起来一门新的边缘技术—多传感器信息融合（Multisensor Information Fusion）。

在多传感器信息融合领域，信息融合最优滤波广泛应用到地震勘探[1]、信号处理[2]和目标跟踪[3]等领域。在国内外发表的大量与信息融合最优滤波理论的相关文献，针对不同的系统模型提出不同的融合算法。文献[4]针对带位置和速度观测的两传感器系统，基于ARMA模型的现代时间序列分析方法，应用基于Riccati方程的经典Kalman滤波方法，在线性最小方差信息融合准则下，分别给出按矩阵加权、对角阵加权和标量加权的三种信息融合滤波器。但是，在ARMA新息模型的构造时，需要进行左素分解。文献[5]针对两传感器单通道系统，基于ARMA模型的现代时间序列分析方法和增广的状态空间模型，提出最优信息融合Wiener信号滤波器，并给出了计算最优加权系数的方法，即局部滤波器误差方差和局部滤波器之间协方差的计算公式，提高了滤波器的精度。文献[6]针对带有色噪声的多传感器线性时变系统，基于一阶时间相关的Markov色噪声观测模型，给出采用状态扩维法和量测差分法进行状态滤波，并提出两种加权融合方法，通过协方差分析技术和仿真实验证明了两种加权观测融合滤波与集中式融合滤波精度相同。

在自然界和各类工业控制系统中，信号在采集、传输和接收等过程都需要消耗一定的时间，此时，系统的输出和输入之间往往会产生时间上的延迟，称之为时滞现象。一个系统中同时存在一个或是多个时滞对象，则可称其为时滞系统。由于时滞系统中存在观测输出量不能及时反映系统输入量的现象，无法针对观测信息及时调整相应的控制量，导致系统稳定性下降、系统性能变差等问题。所以，对于这类系统的研究具有很重要的意义。

针对带观测滞后和观测噪声的多传感器系统，目前已有的数据处理方法主要有如下方法：增广系统法[7]、观察变换法[8]和时滞嵌入法[9]等。文献[10]采用增广系统法将时滞系统转换为无时滞系统，进而获得无时滞系统的Kalman滤波方法，最终解决带时滞的系统状态估计问题，但是，当时滞较长时，状态增广后的维数较高，导致计算负担显著增加，因此增广系统法适用于维数较低、时滞较小的系统。文献[11]中针对带范数有界不确定性的离散时间系统的鲁棒Kalman滤波问题，该系统包含实时观测（d0=0）和滞后观测（d1>0，即一个滞后）。采用增广系统解决时滞问题时，会产生高维系统，当时滞较大时，付出的计算代价过高。为了客服该问题，文献[11]提出了一种新的方法，基于新息重组方法求解两个参数化的Riccati差分方程，且两个Riccati递归方程与系统的维数相同，从而大大提高了计算效率。文献[12]采用观察变换法重新排列有时滞的观测数据，将其转化成为不同观测系统的无时滞观测数据，并通过Krein空间，将离散时滞系统的估计问题转化为Krein空间中的估计问题，进而提高了系统精度。643ADA44-9CA4-4DAE-9F04-0B6588D70579

本文采用时滞嵌入法将时滞嵌入到状态转移阵中。基于现代时间序列分析方法，应用自回归滑动平均模型（ARMA）与状态空间模型之间的转化公式。首先，通过模型转换，将信号包含到状态中，同时也将时滞部分嵌入到转移矩阵中，进而将信号的反卷积问题转变为状态滤波的问题。然后，采用Gevers-Wouters算法将时滞系统模型转变为ARMA信息模型，进而得到局部Wiener反卷积滤波器。最后，在线性最小方差意义下，获得按标量加权最优融合的无偏估计。仿真例子验证了算法的有效性和正确性。

1  问题阐述

考虑信号模型表达式如下：

（1）

（2）

（3）

其中，i=1，…，L，t为离散时间，为第i个传感器的观测输出，s（t）为输入信号，ξi（t）为传感器观测噪声。

由表达式（3）可知，信号s（t）为ARMA信号，yi（t）为观测输出，ηi（t）为有色观测噪声，ξi（t）白色观测噪声，ki为观测延迟，且ki≥0。其中，ξi（t）是零均值，方差为的不相关白噪声。A（q-1）C（q-1）Pi（q-1）Mi（q-1）Ψ（q-1）Φ（q-1）的形式如下，其中：a0=1，pi，0=1，φ0=1，Ψ0≠0，c0=0。

X（q-1）=x0+x1q-1+…+xnxq-nx

假设1：ei（t），w（t）为零均值，方差为和不相关的白噪声。

假设2：观测数据yi（t）以概率1有界。

其中，na为A的阶次，ni，p为Pi（q-1）的阶次，nb为B的阶次，L为传感器个数。

2  多传感器ARMA信号反卷积模型转换

将多传感器系统（1）～（3）中的各表达式分别轉化为状态方程。应用自回归滑动平均（ARMA）模型到状态空间模型的伴随形转化方法[13]，将观测方程转化为增广状态方程形式。

首先，对公式（3）进行讨论。使MA项的首系数为零。

A（q-1）s（t）=C（q-1）w（t）=C（q-1）q-1qw（t）   （4）

设，则可得：

（5）

在应用模型转化方法前，进行补齐系数操作：

如果na如果nc

P1（q-1）=1+0.9q-1+0.2q-2，P2（q-1）=1+1q-1+0.16q-2，P3（q-1）

=1+0.7q-1+0.06q-2

A（q-1）=1-1.8q-1+1.05q-2-0.2q-3，C（q-1）=q-1+0.3q-2

Ψ（q-1）=0.5+q-1，Φ（q-1）=1-q-1+0.16q-2，k1=3，

k2=2，k3=1

，，，，，，

且，a0=1，p0=1。其中：k≥0，q-1为滞后算子。

主要目的是，基于观测yi（t），yi（t-1），……，i=1，…L，求取最优反卷积信息滤波器。

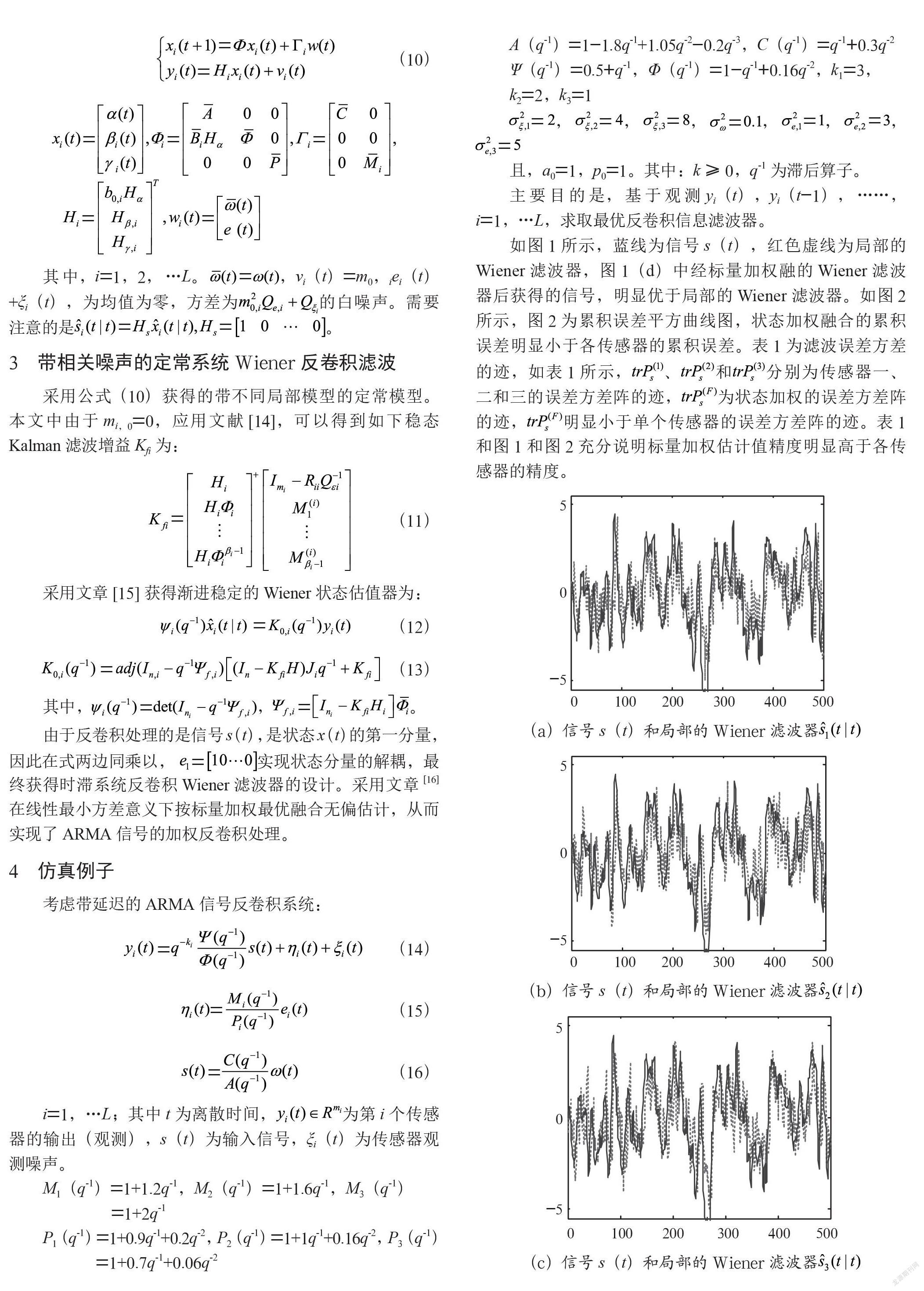
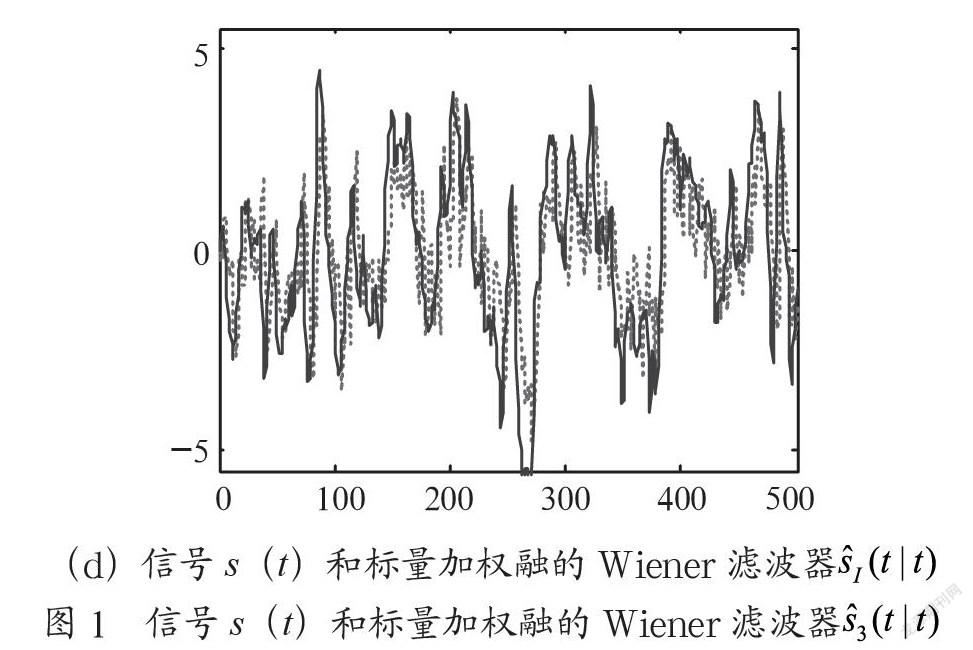
如图1所示，蓝线为信号s（t），红色虚线为局部的Wiener滤波器，图1（d）中经标量加权融的Wiener滤波器后获得的信号，明显优于局部的Wiener滤波器。如图2所示，图2为累积误差平方曲线图，状态加权融合的累积误差明显小于各传感器的累积误差。表1为滤波误差方差的迹，如表1所示，、和分别为传感器一、二和三的误差方差阵的迹，为状态加权的误差方差阵的迹，明显小于单个传感器的误差方差阵的迹。表1和图1和图2充分说明标量加权估计值精度明显高于各传感器的精度。

5  结  论

本文针对多传感器系统模型中存在不同时滞和不同有色噪声的单通道ARMA信号，通过模型变换和时滞嵌入，将信号包含到状态中，并提出反卷积Wiener滤波器，进而通过状态加权得到单通道ARMA信号最优标量加权融合反卷积Wiener滤波器。该Wiener反卷积滤波器适用于多传感器模型在受到不同噪声环境干扰和时滞影响下的情形。仿真例子证明其有效性及正确性。

参考文献：

[1] MENDEL J.White-noise estimators for seismic data processing in oil exploration [J].IEEE Transactions on Automatic Control，1977，22（5）：694-706.

[2] CANEDO-RODR?GUEZ A，LVAREZ-SANTOS V，REGUEIRO C V，et al.Particle filter robot localisation through robust fusion of laser，WiFi，compass，and a network of external cameras [J].Information Fusion，2016，27：170-188.

[3] SUN S，LIN H，MA J，et al.Multi-sensor distributed fusion estimation with applications in networked systems：A review paper [J].Information Fusion，2017，38：122-134.

[4] 孟華，石莹，邓自立.带位置和速度观测的信息融合Kalman跟踪滤波器 [J].科学技术与工程，2005（1）：14-18.

[5] 毛琳，邓自立.信息融合WIENER信号滤波器 [J].黑龙江大学自然科学学报，2005（4）：517-520+524.

[6] 余安喜，梁甸农，杨宏文，等.色噪声下的多传感器量测融合 [J].电子与信息学报，2006（11）：2050-2053.

[7] XIAO L，ZHANG H，WEI W，et al.Kalman filtering for multiple time-delay systems [J].Automatica，2005，41（8）：1455-1461.

[8] SUN X J，DENG Z L.Information fusion Wiener filter for the multisensor multichannel ARMA signals with time-delayed measurements [J].Iet Signal Processing，2009，3（5）：403-415.

[9] GAO Y，DENG Z L.Covariance Intersection fusion Wiener signal estimators based on embedded-time-delay ARMA model [C]//2012 15th International Conference on Information Fusion.Singapore：IEEE，2012：1447-1453.

[10] HOHN M E.Linear estimation [M].Berlin：Springer Netherlands，1999.

[11] LU X，ZHANG J J.Robust Kalman filtering for wireless sensor networks systems with measurement delay [C]//Proceedings of the 30th Chinese Control Conference.Yantai：IEEE，2011：5054-5057.

[12] 焉杰.多传感器时滞系统信息融合及其仿真 [D].青岛：山东科技大学，2010.

[13] 邓自立.信息融合滤波理论及其应用 [M].哈尔滨：哈尔滨工业大学出版社，2007.

[14] SUN X J，GAO Y，DENG Z L，et al.Multi-model information fusion Kalman filtering and white noise deconvolution [J].Information Fusion，2010，11（2）：163-173.

[15] RAN C J，DENG Z L.Decoupled Wiener state fuser for descriptor systems [J].Journal of Control Theory and Applications，2008，6（4）：365-371.

[16] SUN S L.Multi-sensor information fusion white noise filter weighted by scalars based on Kalman predictor [J].Automatica，2004，40（8）：1447-1453.

作者简介：孙赫（1987—），男，汉族，黑龙江绥化人，中级工程师，硕士研究生，研究方向：信息融合;通讯作者：封文清（1988—），女，汉族，江苏徐州人，博士研究生，研究方向：信息融合、多目标进化优化与应用。643ADA44-9CA4-4DAE-9F04-0B6588D70579