转盘式多足仿生机器人的运动学分析及优化

张春燕，丁 兵，何志强，杨 杰

（1.上海工程技术大学机械与汽车工程学院，上海 201600；2.厦门ABB开关有限公司，福建 厦门 361000）

作为科技含量很高的生产工具，机器人在人类生产和生活中扮演着日益重要的角色。与轮式、履带式移动机器人相比，足式移动机器人在未知环境下具有独特的优越性能：足端可离散优化的特点使机器人能找到最优地面支撑点以适应各种地形；多自由度、腿长可伸缩调节的特点使机器人可保持机体重心平稳，不易翻倒；机体与地面相互分离的特点使机器人可在不规则的地形环境中任意调节位姿，无需考虑各支撑点相对于机体的位置。随着对足式移动机器人的深入研究及其应用环境的不断更新，通过模仿各种足式动物来开展各种仿生足式移动机器人的设计，已成为机器人研究领域的热点[1-9]。仿生足式移动机器人可广泛应用于抢险救灾、复杂路面运输等领域。

目前，已有许多学者对仿生足式移动机器人进行了相关研究。波士顿动力（Boston Dynamics）公司研发的机器狗BigDog是仿生足式移动机器人的典型代表之一[10]。国内的典型代表有清华大学研发的四足机器人BIOSBOT[11]、哈尔滨工业大学研发的六足仿生机器人Spider[12-13]和上海交通大学研发的具有并联腿部结构的六足机器人Octopus[14-15]等。但是，这些仿生足式移动机器人腿部的驱动器较多，其传感和控制系统复杂，导致研发、制造成本过高。而单自由度仿生机械腿所需的控制器较少，能量利用率高，制造成本可控，引起了机器人研究领域学者的广泛关注。

常用的单自由度仿生机械腿机构主要以Chebyshev连杆机构、Klann连杆机构和Jansen连杆机构为主。其中，由荷兰艺术家Jansen发明的“沙滩怪兽”是以Jansen连杆机构为单元的行走机构，其控制简单且行走高效[16-17]。Jansen连杆机构的能量消耗明显低于Chebyshev连杆机构和Klann连杆机构[18]，其是这3种闭环连杆机构中效率最高的行走机构，故本文选择Jansen连杆机构作为多足仿生机器人的机械腿机构。

为此，笔者基于足式移动机器人的特点及单自由度Jansen连杆机构，结合曲柄摇杆机构，创新性地设计了一款转盘式多足仿生机器人，其可自主切换多对足。首先，以所设计机器人的单条仿生机械腿为例，利用旋量理论和复数矢量法对其进行自由度验证和运动学分析；然后，对仿生机械腿足端的运动轨迹进行分析并得到其优化方向，同时根据实际给定要求得出其设计参数，并对传动机构进行优化；最后，通过制作转盘式多足仿生机器人的理论样机来验证其可行性。

1 仿生机械腿机构原理及自由度分析

1.1 仿生机械腿机构原理

基于Jansen连杆机构设计多足仿生机器人的机械腿结构，其机构原理如图1所示。为了增加腿部机构的刚度，由2个三角桁架（BO2C和DEF）通过7个转动副与6根连杆组成仿生机械腿，并以连接曲柄O1A和三角桁架BO2C的固定连杆O1O2作为机架。曲柄O1A转动时带动其他杆件运动，从而实现触地、迈进、抬足和悬空前摆等动作。通过改变各杆件的参数可得到不同的足端运动轨迹。

图1 仿生机械腿机构原理Fig.1 Mechanism principle of bionic mechanical leg

1.2 仿生机械腿自由度分析

以仿生机械腿中连接曲柄和机架的转动副O1为原点，建立固定坐标系，其中机架O1O2与X轴有一定夹角。分析仿生机械腿机构各关节的运动螺旋，如图2所示。

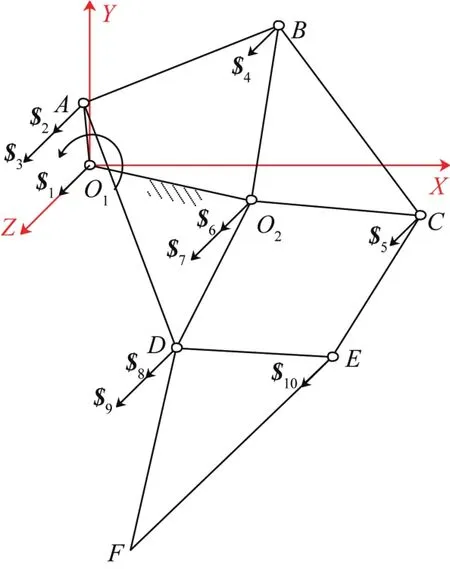
图2 仿生机械腿机构各关节的运动螺旋示意Fig.2 Motion screw diagram of each joint of bionic mechanical leg mechanism

基于图2，利用螺旋理论[19-20]来计算仿生机械腿机构的自由度，其运动螺旋系可表示为：

式中：$i（i=1，2，…，10）为仿生机械腿机构各关节的运动螺旋；ai、bi为不同实数。

由此可得，仿生机械腿机构的反螺旋系为：

由式（2）可知，该仿生机械腿机构有3个反螺旋，说明其具有3个公共约束，即阶数为3，冗余约束数和局部自由度均为0，故其自由度M为：

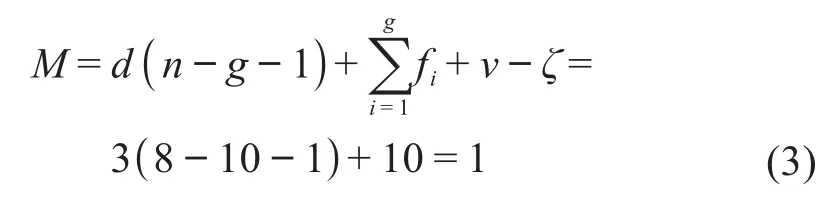
式中：d为机构阶数，d=6-λ；λ为机构公共约束数；n为机构总构件数；g为机构总运动副数量；fi为第i个运动副的自由度，i=1，2，…，10；v为机构的独立冗余约束数；ζ为机构的局部自由度。

2 仿生机械腿运动学分析

通过分析多足仿生机器人机械腿输入端与输出端的位置关系来构建其运动学数学模型，并基于该模型得到各关键部位的位置及运动轨迹，以实现整个机器人的可行性评估和优化。将所设计的仿生机械腿机构简化为平面连杆机构，并对其杆组进行拆分，如图3所示。利用复数矢量法对各杆组进行运动学分析。

图3 仿生机械腿机构杆组拆分示意Fig.3 Schematic diagram of disassembly of rod group of bionic mechanical leg mechanism

由图3可知，该仿生机械腿机构的杆组可拆分为以下几个部分：机架O1O2、曲柄O1A和3个Ⅱ级杆组（AB-BO2C、CE-EDF和AD-DO2）。按照O1→A→B→C→E→F的顺序，对仿生机械腿机构各杆组进行运动学分析。定义仿生机械腿机构中各连杆的长度，如表1所示。

表1 仿生机械腿机构各连杆的长度定义Table 1 Definition of length of each connecting rod of bionic mechanical leg mechanism

1）机架O1O2和曲柄O1A的运动学分析。

已知机架O1O2和曲柄O1A与X轴正方向的夹角分别为α1和β，基于欧拉公式得到机架和曲柄所对应的矢量rO1O2和rO1A的复数形式，可表示为：

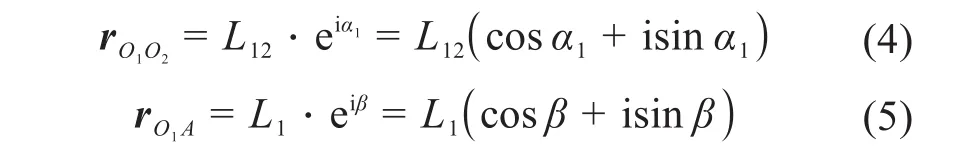
2）Ⅱ级杆组AB-BO2C的运动学分析。

Ⅱ级杆组AB-BO2C在固定坐标系O1-XY中的位置如图4所示。

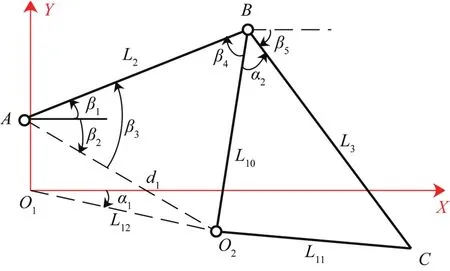
图4 固定坐标系中Ⅱ级杆组AB-BO2C的位置示意Fig.4 Position diagram of class-II rod groupAB-BO2Cin fixed coordinate system

由图4可得，连杆O1B、O1C所对应的矢量rO1B和rO1C的复数形式分别为：

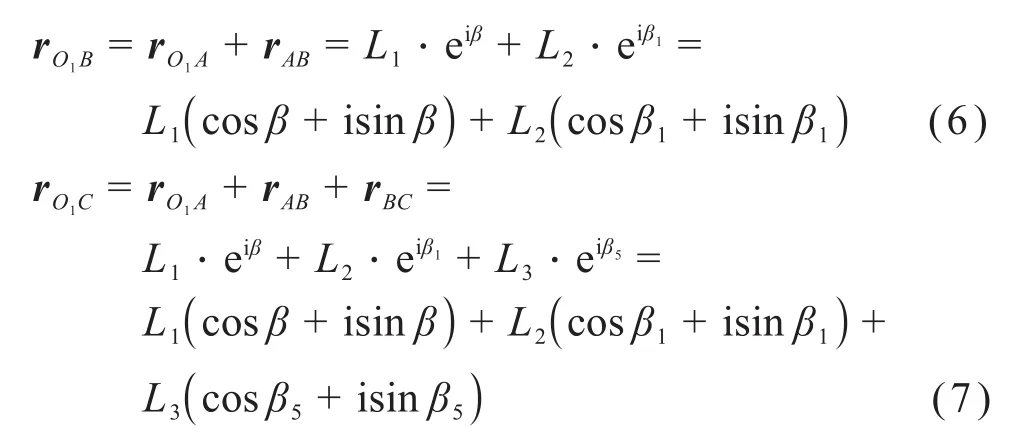
3）Ⅱ级杆组AD-DO2的运动学分析。

Ⅱ级杆组AD-DO2在固定坐标系O1-XY中的位置如图5所示。

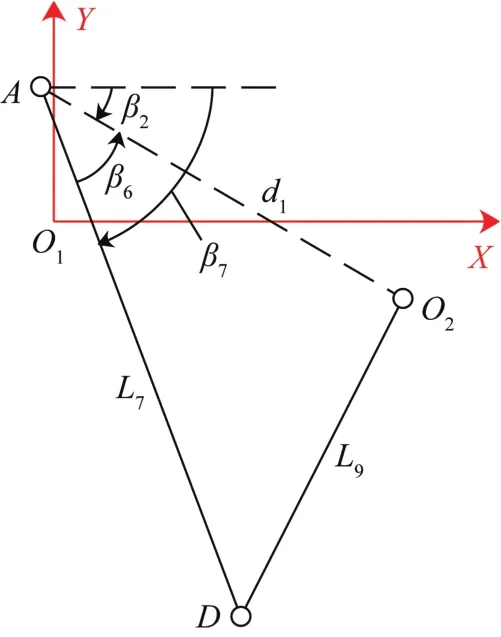
图5 固定坐标系中Ⅱ级杆组AD-DO2的位置示意Fig.5 Position diagram of class-II rod groupAD-DO2 in fixed coordinate system

由图5可得，连杆O1D所对应的矢量rO1D的复数形式为：

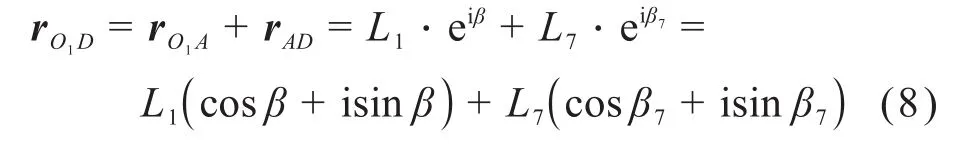
4）Ⅱ级杆组CE-EDF的运动学分析。

Ⅱ级杆组CE-EDF在固定坐标系O1-XY中的位置如图6所示。

图6 固定坐标系中Ⅱ级杆组CE-EDF的位置示意Fig.6 Position diagram of class-II rod groupCE-EDFin fixed coordinate system

由图6可得，连杆O1F所对应的矢量rO1F的复数形式为：

基于式（9），可得F点（即仿生机械腿足端）的横、纵坐标为：

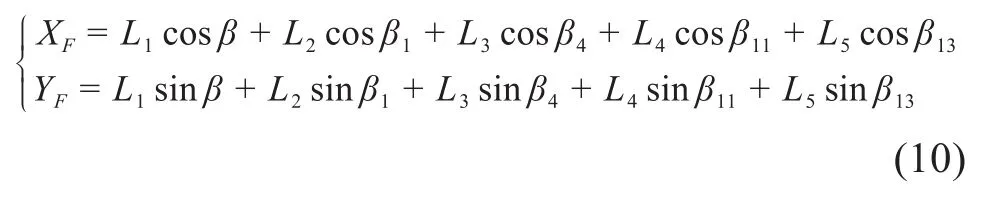
根据式（10）可获得仿生机械腿足端的运动轨迹，可为后续多足仿生机器人的步态生成提供理论基础。

3 仿生机械腿足端轨迹分析与优化

考虑到整个多足仿生机器人的结构合理性及轻量化需求，同时为提高其行走效率[21]，结合图1所示各连杆的长度关系，对仿生机械腿机构进行尺度综合。各连杆的预设长度如表2所示，利用SolidWorks软件对仿生机械腿进行建模，如图7所示。

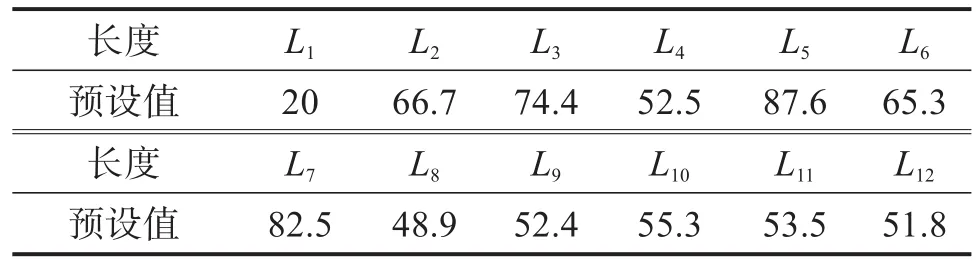
表2 仿生机械腿机构各连杆的预设长度Table 2 Preset length of each connecting rod of bionic mechanical leg mechanism 单位：mm

图7 仿生机械腿三维模型Fig.7 Three-dimensional model of bionic mechanical leg

3.1 足端运动轨迹分析

将图7所示的仿生机械腿三维模型导入ADAMS（automatic dynamic analysis of mechanical systems，机械系统动力学自动分析）仿真软件，并在曲柄O1A处添加驱动电机。完成相关参数设置后，通过仿真得到仿生机械腿各关键部位的运动轨迹，如图8所示。由图可知，当曲柄末端和足端的运动轨迹同向时，膝关节以相反的方向运动。

图8 仿生机械腿各关键部位的运动轨迹示意Fig.8 Motion trajectory of each key part of bionic mechanical leg

任何动物行走时，其足端的运动轨迹与地面越平行，即足端着地点和离地点的连线越长且越平缓，说明其步幅越大且越平稳；足端抬得越高，则越障能力越强。为获得仿生机械腿足端的最优运动轨迹，对曲柄转动一周（曲柄与机架的夹角发生变化）时足端的位置进行分析，结果如图9所示。

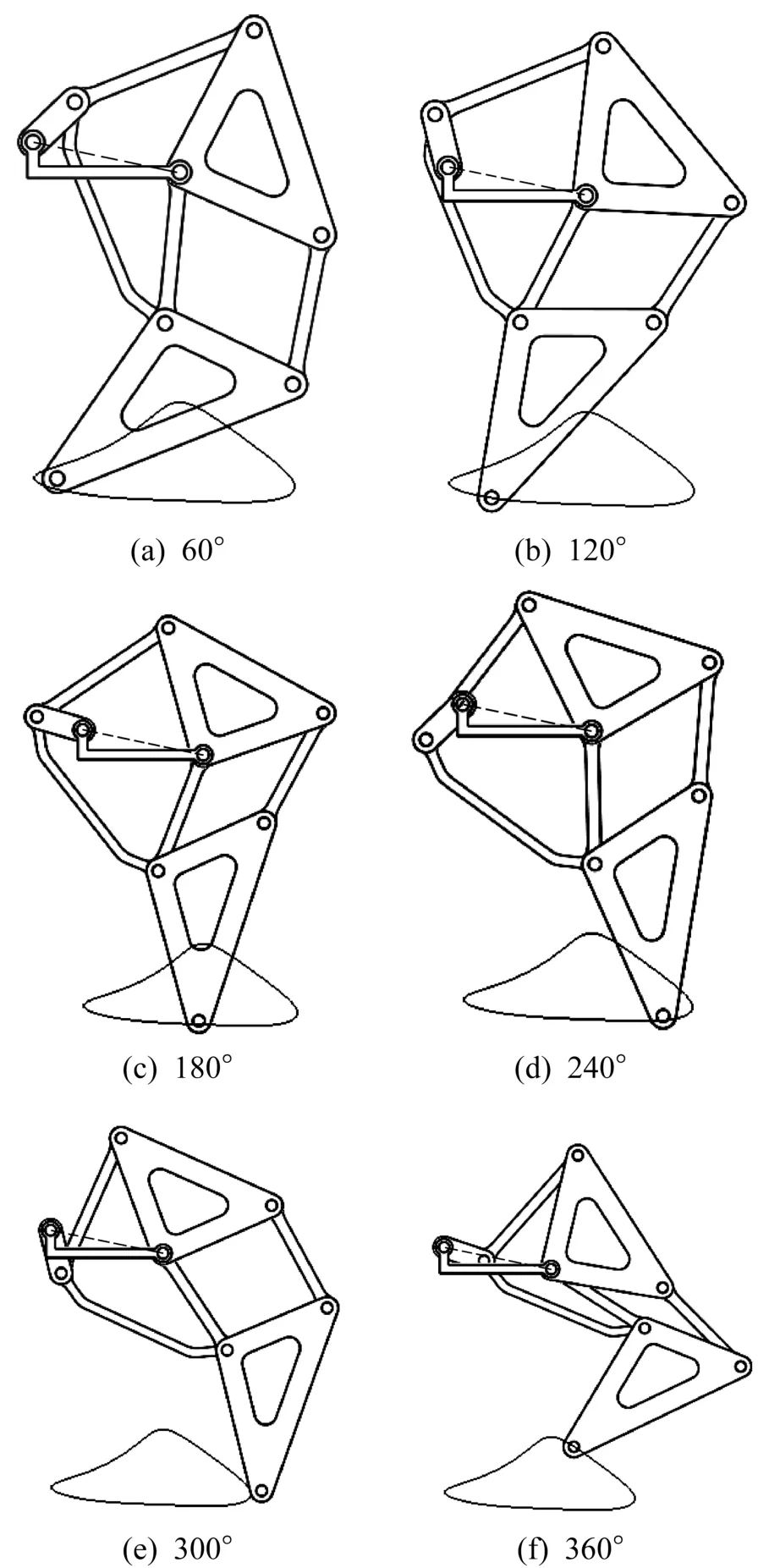
图9 曲柄与机架夹角不同时仿生机械腿足端的位置对比Fig.9 Comparison of foot end position of bionic mechanical leg with different angle between crank and frame

由图9可以看出，当曲柄与机架的夹角以60°为间隔变化时，仿生机械腿足端从图9（a）所示的着地点（夹角为60°）慢慢移动到图9（c）所示的中点（夹角为180°），再到图9（e）所示的离地点（夹角为300°），最后到图9（f）所示的近最高点（夹角为360°）。由此可知，仿生机械腿足端的位置会随曲柄的转动而改变，找到足端运动轨迹的变化规律，以实现其优化。

根据式（10），通过MATLAB软件编程求出仿生机械腿足端的理论运动轨迹，并与基于ADAMS软件得到的仿真运动轨迹进行对比，结果如图10所示。通过对比发现，仿生机械腿足端的理论运动轨迹与仿真运动轨迹近似重合，验证了理论分析的正确性。

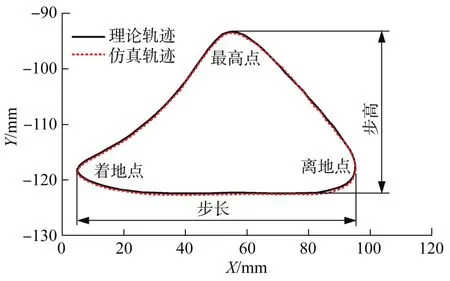
图10 仿生机械腿足端运动轨迹对比Fig.10 Comparison of motion trajectories of bionic mechanical leg foot end

3.2 足端运动轨迹优化

定义仿生机械腿足端运动轨迹的步长为Ls、步高为Lh，基于Jansen连杆机构的运动轨迹优化方案[22-26]，分别对曲柄长度和机架的水平倾角进行优化分析。

首先，只改变曲柄长度，通过仿真得到仿生机械腿足端运动轨迹的变化情况，如图11所示。由图可知，在一定范围内，仿生机械腿足端运动轨迹的步高和步长均随曲柄长度的增大而增大；随着曲柄长度的增大，足端运动轨迹步高的变化是非线性的，而步长的变化是线性的，可用以下等式表示：

图11 不同曲柄长度下仿生机械腿足端运动轨迹的变化情况Fig.11 Changes of foot end motion trajectory of bionic mechanical leg under different crank lengths

然后，只改变机架的水平倾角，通过仿真得到仿生机械腿足端运动轨迹的变化情况，如图12所示。由图可知，仿生机械腿足端运动轨迹的步长和步高均随机架水平倾角的增大而减小，其中步长的减小幅度较小，而步高的减小幅度较大。

图12 不同机架水平倾角下仿生机械腿足端运动轨迹的变化情况Fig.12 Changes of foot end motion trajectory of bionic mechanical leg under different horizontal inclination angles of frame

综上所述，在仿生机械腿其余参数不变的情况下，其足端运动轨迹步长的变化范围为（0，96.6）mm，步高的变化范围为（0，77.7）mm。可通过增大曲柄长度或减小机架水平倾角来增大该仿生机械腿足端运动轨迹的步长和步高，从而提高其爬坡和越障能力。在实际设计时，可输入单条仿生机械腿足端运动轨迹的步长和步高需求，以对多足仿生机器人进行整体设计。

4 转盘式多足仿生机器人设计

4.1 机器人的技术指标要求

转盘式多足仿生机器人的技术指标要求如表3所示。

表3 转盘式多足仿生机器人的技术指标要求Table 3 Technical index requirements of rotary multi-legged bionic robot

4.2 机器人结构设计

4.2.1 转盘式传动机构设计

多足仿生机器人是基于曲柄摇杆原理进行传动的，但传统传动机构所需的驱动电机较多且功耗较大。为此，本文创新性地提出了一种转盘式传动机构，其结构类似于滚针轴承，如图13所示。在转盘和支架之间套入向心滚针和保持架组件，以减少摩擦和提高传动效率。转盘式多足仿生机器人由多对足组成，每对足共用1个动力输入点，通过连杆与转盘上的偏心轴连接，只需1个驱动电机带动转盘转动就可使多对处于不同相位的仿生机械腿运动。

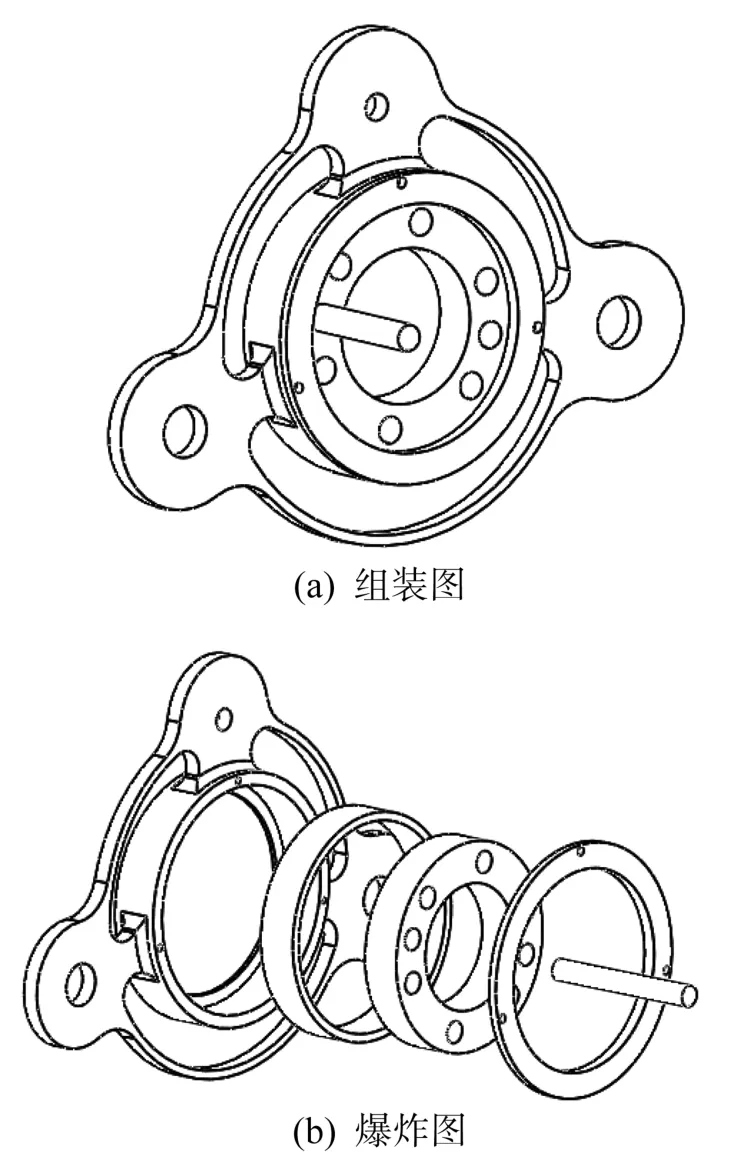
图13 转盘式传动机构结构示意Fig.13 Structure diagram of rotary transmission mechanism

如图14所示，对转盘上的等径圆作开孔处理，每间隔30°开一个圆孔。通过传动轴互成120°，90°和60°装配连接，可实现3对足、4对足和6对足的组合，从而适应不同的场景需求。

图14 不同对足组合时转盘的传动轴分布示意Fig.14 Schematic diagram of transmission shaft distribution of rotary disc with different pairs of feet combined

4.2.2 转动关节及自适应足端设计

对仿生机械腿的转动关节进行优化设计。如图15所示，将2个推力球轴承间隔放置在杆件之间，避免了摩擦面的出现，增大了转动副对侧向力的有效抵抗能力。

图15 仿生机械腿转动关节结构示意Fig.15 Structure diagram of rotation joint of bionic mechanical leg

仿生机械腿足端采用自适应设计，其结构如图16所示。当机械腿离地时，其足端在重力作用下自然下垂；当机械腿落地时，自适应足端底部的圆弧曲面可根据地形紧贴地面，实现机器人机体的稳定支撑。

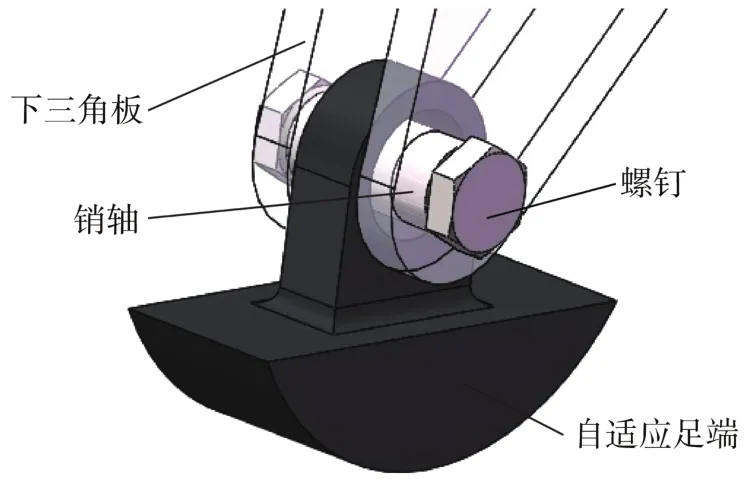
图16 自适应足端结构示意Fig.16 Structure diagram of adaptive foot end

4.2.3 整体设计

基于Jansen连杆机构的转盘式多足仿生机器人具有结构紧凑、控制简单、运动灵活平稳、越障能力强、驱动电机少和零转弯半径等优点。由多条仿生机械腿和转盘式传动机构装配而成的多足仿生机器人的整体结构如图17所示，其两侧各有3对足。得益于转盘式传动机构，该机器人的整体尺寸小于同类机器人，仅为334 mm×220 mm×188 mm。

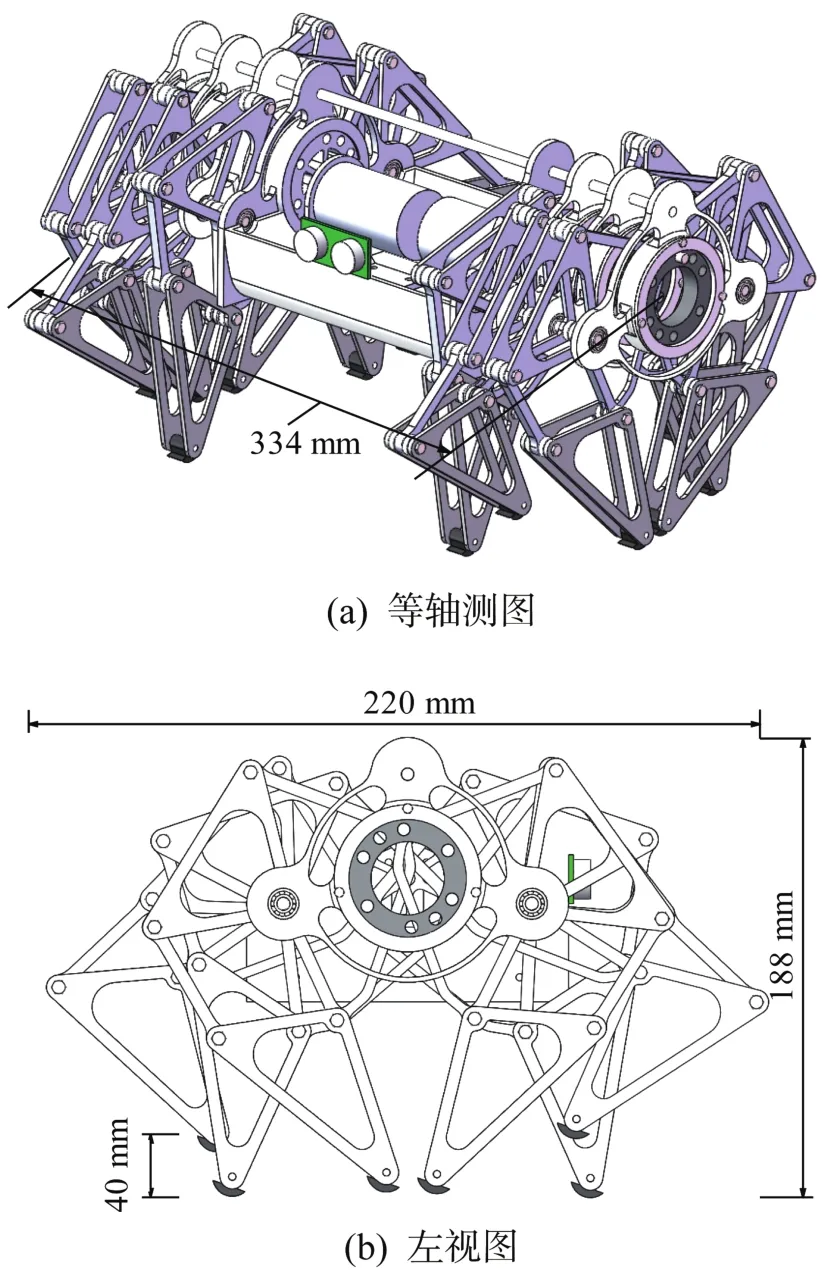
图17 转盘式多足仿生机器人整体结构示意Fig.17 Overall structure diagram of rotary multi-legged bionic robot

4.3 机器人步态的时序分析

步态时序对移动机器人的运动特性和稳定性有直接的影响。鉴于所设计的转盘式多足仿生机器人的整体结构对称，仅取其一侧的3对足进行分析。根据图9，将曲柄与机架的夹角为60°～300°时定义为支撑相，夹角为0°～60°及300°～360°时定义为悬空相。假设曲柄以角速度ω=60（°）/s转动，转盘式多足仿生机器人的步态如图18所示。

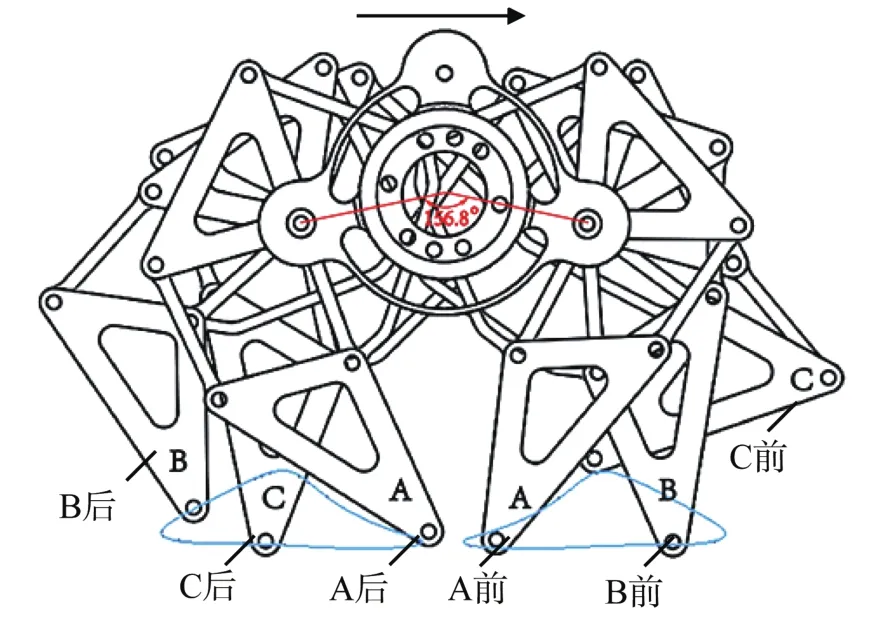
图18 转盘式多足仿生机器人的步态示意Fig.18 Gait diagram of rotary multi-legged bionic robot

由图14（a）和图18可知，该转盘式多足仿生机器人每对足中曲柄中心与转盘中心连线之间的夹角为156.8°，且每对足的传动轴相位差为120°。定义3对足从前往后依次为对足A、对足B和对足C，机器人沿图示方向移动，则各足的曲柄与机架的夹角关系如下。

设对足A中前足的曲柄与机架的夹角为θ1，则有：

1）对足A中后足的曲柄与机架的夹角θ2=360°-156.8°-θ1。

2）对足B中前足的曲柄与机架的夹角θ3=θ1-120°。

3）对足B中后足的曲柄与机架的夹角θ4=θ2-120°。

4）对足C中前足的曲柄与机架的夹角θ5=θ1-240°

5）对足C中后足的曲柄与机架的夹角θ6=θ2-120°。

由上述关系可得转盘式多足仿生机器人的步态时序图，如图19所示。其中，纵坐标值为0表示该足处于支撑相，纵坐标值为1表示该足处于悬空相，T为步态周期。通过分析可知，在单个步态周期内，支撑相占整个步态周期的2/3，悬空相占整个步态周期的1/3；3对足在大部分时间内都处于四足同时着地的状态，连接着地足端可形成一个四边形区域，说明该机器人移动时具有较大的着地面积，其稳定性很强。

图19 转盘式多足仿生机器人的步态时序图Fig.19 Gait sequence diagram of rotary multi-legged bionic robot

5 转盘式多足仿生机器人功能分析及样机实验

5.1 功能分析

5.1.1 直行与转向分析

当转盘式多足仿生机器人在平坦路况下行走时，其所有机械腿的曲柄转速均相同，则可确定其直行速度。由3.1节的足端运动轨迹分析可知，仿生机械腿的跨步步长为90 mm，故曲柄完成一个周期的转动（转动360°）时，所设计的转盘式多足仿生机器人可移动270 mm，则其移动速度v与曲柄转动角速度ω的关系为：

转盘式多足仿生机器人的转向功能通过控制2个电机反向转动来实现，可完成零半径转弯，极大地提高了机器人在狭窄空间中的运动能力。

5.1.2 爬坡分析

如图20所示，当转盘式多足仿生机器人攀爬坡度为α的斜坡时，须确保其机身不发生倾倒，则该机器人所能爬过的斜坡的最大坡度可由式（13）计算得到：

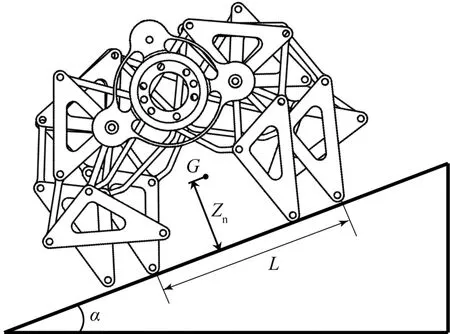
图20 转盘式多足仿生机器人爬坡示意Fig.20 Schematic diagram of rotary multi-legged bionic robot climbing

式中：Zn为机器人质心到地面的距离；L为支撑长度。

通过计算可得，在不考虑外部摩擦力和电机功率等因素的理想条件下，转盘式多足仿生机器人能爬过最大坡度为15°的斜坡。

5.1.3 越障分析

1）攀越台阶。

如图21所示，转盘式多足仿生机器人攀越台阶时需经过抬腿和前摆才能踏上台阶，其所能攀越的最大台阶高度主要取决于其最大抬腿高度。由表3可知，该机器人的最大抬腿高度为30 mm，则其能攀越最大高度为30 mm的台阶。

图21 转盘式多足仿生机器人攀越台阶示意Fig.21 Schematic diagram of rotary multi-legged bionic robot climbing step

2）跨越壕沟。

图22所示为转盘式多足仿生机器人跨越壕沟的过程，其所能跨越的最大壕沟宽度取决于其仿生机械腿的最大跨步步长。通过仿真可以得到该机器人单条仿生机械腿的最大跨步步长为90 mm，则其能跨越最大宽度为90 mm壕沟[27-28]。

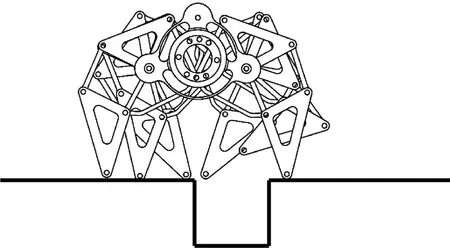
图22 转盘式多足仿生机器人跨越壕沟示意Fig.22 Schematic diagram of rotary multi-legged bionic robot crossing trench

5.2 样机实验

根据上文对转盘式多足仿生机器人的设计和分析，优化并加工装配其样机，如图23所示。机器人样机的参数详见表4。

图23 转盘式多足仿生机器人样机Fig.23 Prototype of rotary multi-legged bionic robot

表4 转盘式多足仿生机器人样机参数Table 4 Parameters of rotary multi-legged bionic robot prototype

为验证所设计转盘式多足仿生机器人的可行性，利用样机进行相关实验，以测试样机在真实地形下的机动性和稳定性，同时测量样机的技术指标参数并与设计需求进行对比，以实现对不合理设计的改进。

5.2.1 平地直行及转向实验

图24所示为转盘式多足仿生机器人在平坦地面上直行和转向的实验现场。在实验过程中，该机器人样机行走正常，且可以通过控制系统实现前进、后退、停止以及零半径转向的功能。由于零件的加工精度及部件的安装误差，该机器人在转向过程中可能会造成其腿部杆件扭转，导致腿部机构之间相互干扰，有待优化改进。

图24 转盘式多足仿生机器人平地直行和转向实验现场Fig.24 Experiment site of straight ahead and steering of rotary multi-legged bionic robot on flat ground

5.2.2 爬坡实验

转盘式多足仿生机器人的爬坡实验现场如图25所示。结果表明，该机器人可以顺利爬坡，且在平坦坡道上的爬坡速度较快。

图25 转盘式多足仿生机器人爬坡实验现场Fig.25 Climbing experimentsite ofrotary multilegged bionic robot

5.2.3 复杂路面行走实验

转盘式多足仿生机器人在不平坦的草地和鹅卵石路面上行走的实验现场如图26所示。在实验过程中，该机器人可顺利通过鹅卵石路面，但在草地上行走时易受坑洼地形影响，对移动速度的影响较大，甚至可能出现腿部机构卡死的现象。因此，对于多足仿生机器人的设计来说，应依据其应用环境的需求来增大其越障高度。

图26 转盘式多足仿生机器人复杂路面行走实验现场Fig.26 Experiment site of rotary multi-legged bionic robot walking on complex road

6 结论

本文根据Jansen连杆机构的综合优势，研制了一款基于Jansen连杆的转盘式多足仿生机器人。

1）基于Jansen连杆机构设计了多足仿生机器人的机械腿结构，并对其进行运动学分析，为后续的机器人结构优化提供了理论基础。

2）利用MATLAB和ADAMS进行了仿生机械腿足端运动轨迹的生成和仿真分析，验证了理论分析的正确性，并通过优化设计得到了可实现多足仿生机器人在给定需求下平稳、顺畅行走的最优结构参数。

3）创新性地提出了转盘式传动机构，使多足仿生机器人可以变换叠加多对足，提高了其复杂环境适应能力；设计了两侧均有3对足的转盘式多足仿生机器人，并绘制了其步态时序图。

4）利用SolidWorks软件对所设计转盘式多足仿生机器人的直行、爬坡和越障运动进行了仿真，并制作了样机进行相关实验，验证了所设计机器人的可行性。