民用飞机湍流边界层噪声分离技术的应用

李才华，张绍云，杨振超，刘 鹏

（中国商飞民用飞机试飞中心，上海 201323）

0 引言

在飞行状态下，湍流边界层脉动压力是飞机舱内噪声的主要来源之一，其激励飞机蒙皮结构，并通过机体结构复杂的传递路径引起结构振动和舱内噪声，研究其特性对舱内噪声优化设计以及声载荷预测有着重要作用。

在民用飞机领域，国外对湍流边界层噪声的研究较多。Bhat对波音737飞机进行表面声载荷飞行测试，获取了脉动压力功率谱密度；空客公司在A320飞机上进行了一系列噪声相关的飞行测试，获取了不同声源特性及其传递路径，用以修正舱内噪声预测模型。

机体外表面声载荷包含湍流边界层噪声和发动机噪声。采用相干函数方法可分离出湍流边界层噪声。这种信号处理技术首先由Chung提出，在实验室使用3个布置成三角形的麦克风测量同一声源信号，并对每个麦克风加载独立的气流用于模拟风噪，采用相干函数方法将风噪信号从总声压值中分离出来。Cyrille在波音777飞机上进行了表面声载荷飞行测试，并识别出发动机噪声；许坤波等在管道内布置2圈环形麦克风阵列，利用互相关方法得到单音及宽频噪声结果。

湍流边界层预测模型主要分为2大类：一类是壁面压力谱模型，将边界层附近脉动压力的能量按频率分解，得到用于估算脉动压力的功率谱密度，其主要研究者有Robertson、Efimtsov、Rackl等、Goody；另一类是波数-频谱模型，将能量按波长分解，通过大量的试验拟合出经验表达式，其主要研究者有Corcos、Chase、Mellen等。Teresa对 以上 不同的模型进行介绍和对比。对于壁面压力谱模型，在同种工况下，采用Efimtsov和Rackl-Weston模型计算得到的均方压力最大，Goody模型次之，Robertson模型最小；对于波数-频谱模型，采用Corcos和Mellen Elliptical模型在低波数段得到边界层噪声过大的类似预测结果，根据试验结果对Chase模型进行了大量修正，准确性较好。

目前，中国在民用飞机上进行机体表面声载荷测量的飞行试验不多，湍流边界层噪声分离技术的研究也相应较少。本文在飞行试验中获得机体外表面声压数据，采用相干函数方法分离湍流边界层激励，并与Robertson模型计算结果进行对比。

1 相干函数方法

以1个单输入和单输出组成的简单线性系统（如图1所示）为例，对相干函数进行描述。

图1 简单线性系统

假设输入信号为（），输出信号为（），（）为频响函数。（）和（）对应的自谱分别为G（）和G （），二者的互功率谱为G（）。则相干函数为

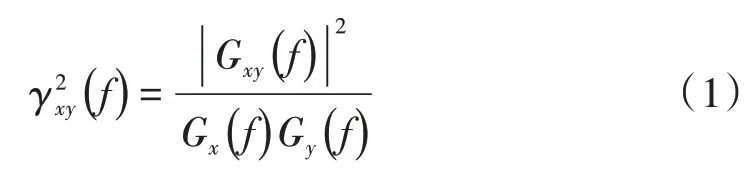
在式（1）中，对于所有的频率都有

如果（）与（）完全不相关，那么相干函数等于零；如果在0~1之间，那么计算出（）信号里与（）相关的部分，用G（）表示

如果1个测试系统有2个麦克风传感器（如图2所示），定义传感器1的信号为（），由相关信号（）和不相关信号（）组成；同样对于传感器2的信号（），由相关信号（）和不相关信号（）组成。

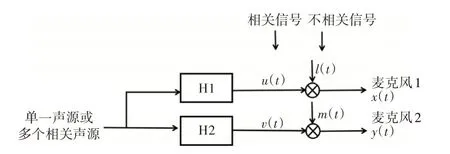
图2 2个传感器组成的系统

（）与（）间的相关函数表示为

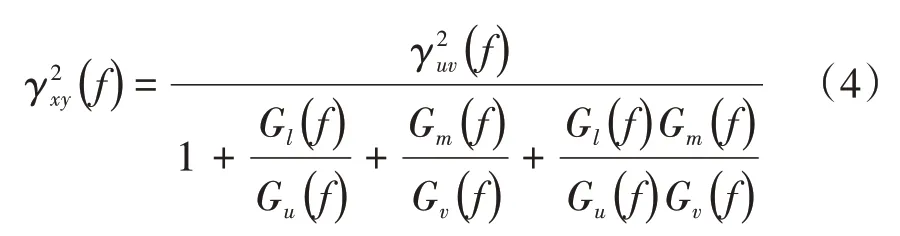
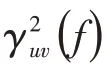
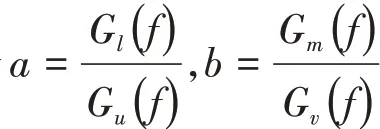
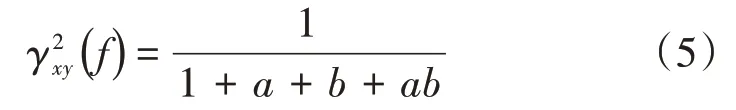
式（5）中有2个未知数和，其求解需引入第3个传感器信号。3个传感器组成的系统如图3所示。

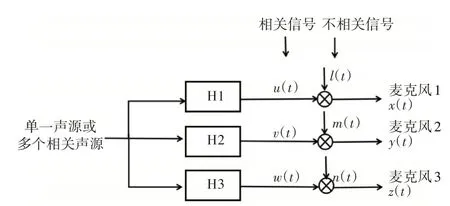
图3 3个传感器组成的系统

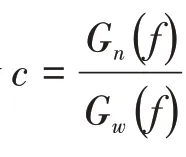
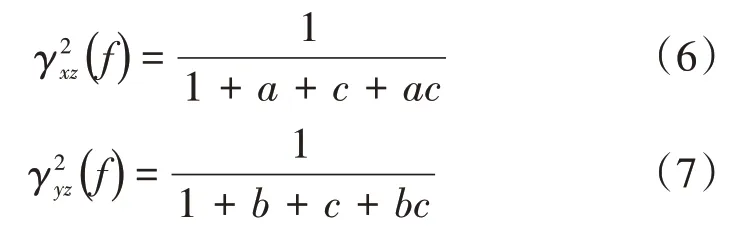
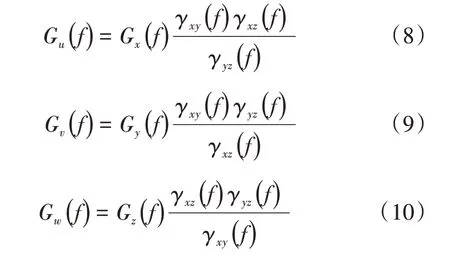
式（8）～（10）等号左边表示各传感器信号中包含的相关成分，可视为相关成分的自谱，详细的推导过程见文献[5]。

在工程应用中，可以先将相关成分的自谱转换为1/3倍频程谱，并根据声压计算公式得到不相关成分的1/3倍频程谱

式中：（）为信号总的1/3倍频程声压级频谱；（）为信号中相关成分的1/3倍频程声压级频谱。

2 Robertson半经验模型

Robertson半经验模型基于Lowson模型发展而来。Lowson公式计算的功率谱在低时有些偏低，而在高时下降太多，因此Robertson模型对Lowson公式进行了改进。

相比于其他壁面压力谱模型，Robertson模型在不同马赫数范围内更能反映实验测量结果。而近年来的模型（如Goody模型）基于低速不可压缩流实验数据提出，可能不适合高飞行马赫数。并且，相比于其他模型，Robertson模型更为简单，参数容易获取，便于应用。

Robertson模型使用了边界层位移厚度δ和当地来流速度U作为归一化参数

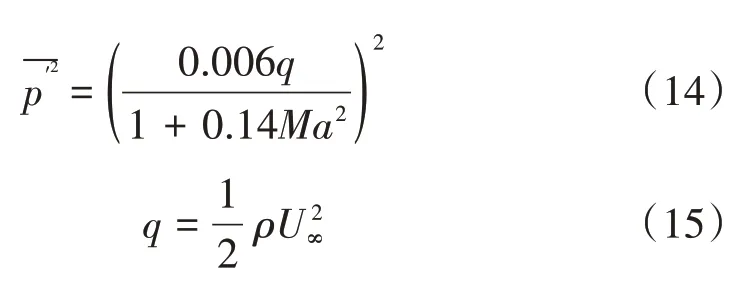
式中：为来流马赫数；为来流动压力；为来流空气密度。

机体表面位移边界层厚度δ的计算使用Bhat的方程

式中：为特征长度，定义为表面声压传感器距离机头的轴向距离；为当地雷诺数。

3 试验介绍

飞行试验在国产某型飞机上进行，使用B&K4948传感器测量机体外表面声载荷。传感器直径为20 mm，厚为2.51 mm，用金属圆盘固定，整个传感器结构（含金属圆盘）直径为30 mm，传感器实物照片如图4所示。传感器频率测量范围为5~20000 Hz，动态噪声变化范围为55~160 dB。橡胶圆盘套在传感器结构（含金属圆盘）上，其作用主要是尽可能消除传感器与机体表面阶差引起的附加风噪。橡胶圆盘内直径为30 mm，外直径为100 mm。

图4 表面声压传感器（含金属和橡胶圆盘）

为了保证传感器在飞行过程中不脱落，使用厚度约为1 mm的双面胶将传感器和圆盘结构粘贴在机体表面，最后覆盖1层薄的航空铝箔胶带加固。传感器导线通过1个改装的舷窗穿入客舱内部，连接同一数采系统，确保传感器数据之间记录的同步性，声压数据采样率为60 kHz。飞行参数通过机上飞参记录器存储，与噪声数据时间同步。试验前后对声压传感器进行标定。3个表面声压传感器在机体等直段外表面形成三角布置结构。其中1、2号传感器在机体上沿航向布置，传感器中心点之间距离为20 cm；2、3号传感器沿垂向布置，传感器中心点之间距离为20 cm。2号传感器中心点沿航向距离机头12.55 m。传感器在机体表面的安装位置如图5所示，在飞机上实际安装的照片如图6所示。

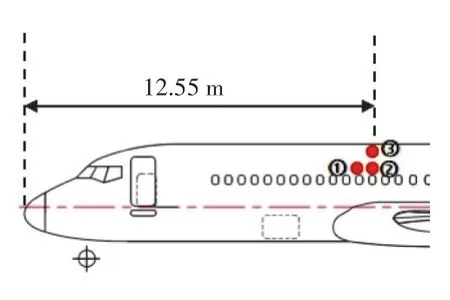
图5 表面声压传感器在飞机上的安装位置

图6 表面声压传感器实际安装照片

4 试验与计算结果对比

飞行试验在10668 m（工况1）和9144 m（工况2）高度上进行，马赫数均为0.78。试验时避开云雨天气，并只在直线稳定飞行时采集数据。

飞机在到达指定高度和目标速度、状态稳定后，由机上工程师记录声压数据，对每个工况截取1 min时长的数据进行分析。

湍流边界层激励的1个重要特性是沿着飞机航向弱相关，沿着飞机垂向完全不相关，由此认为机身表面各点处湍流边界层激励是不相关的成分，而发动机噪声被认为是相关成分。这样，可以使用相干函数的方法进行湍流边界层噪声分离。

在得到3个表面传感器的声压数据后，使用傅里叶变换计算各通道时域信号的自功率谱，频率分辨率为0.5 Hz。计算两两信号之间的互功率谱，为复数形式，通过式（1）得到相干函数。根据式（8）～（10）得到各传感器的相关成分即为发动机噪声，并转换成1/3倍频程声压谱。最后通过式（11）得到湍流边界层噪声，以1/3倍频程谱显示。

在工况1、2下1号表面传感器信号总的噪声和各分量的对比如图7所示。从图中可见，在巡航状态下，湍流边界噪声的贡献量要大于发动机噪声的。总声压在中心频率为1000 Hz附近时达到最高，并在频率越高时，衰减越快。

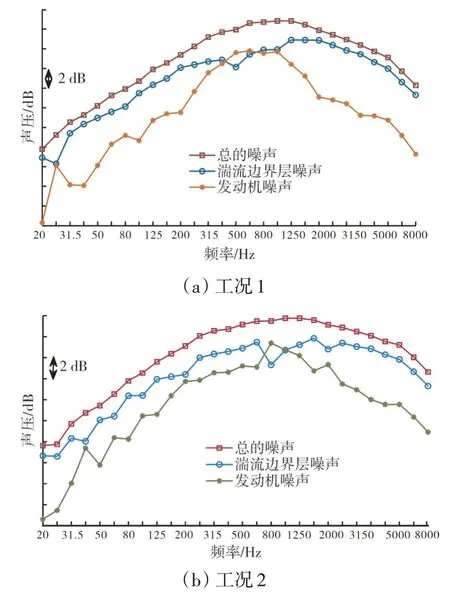
图7 1号传感器湍流边界层噪声的分离

本文使用Robertson模型计算湍流边界层噪声，用到的计算参数见表1。其中飞行高度、马赫数和真空速通过飞参记录器获取，运动黏度参照飞行大气参数标准。边界层位移厚度、动压、特征频率和均方脉动压力根据式（13）～（17）计算得到。

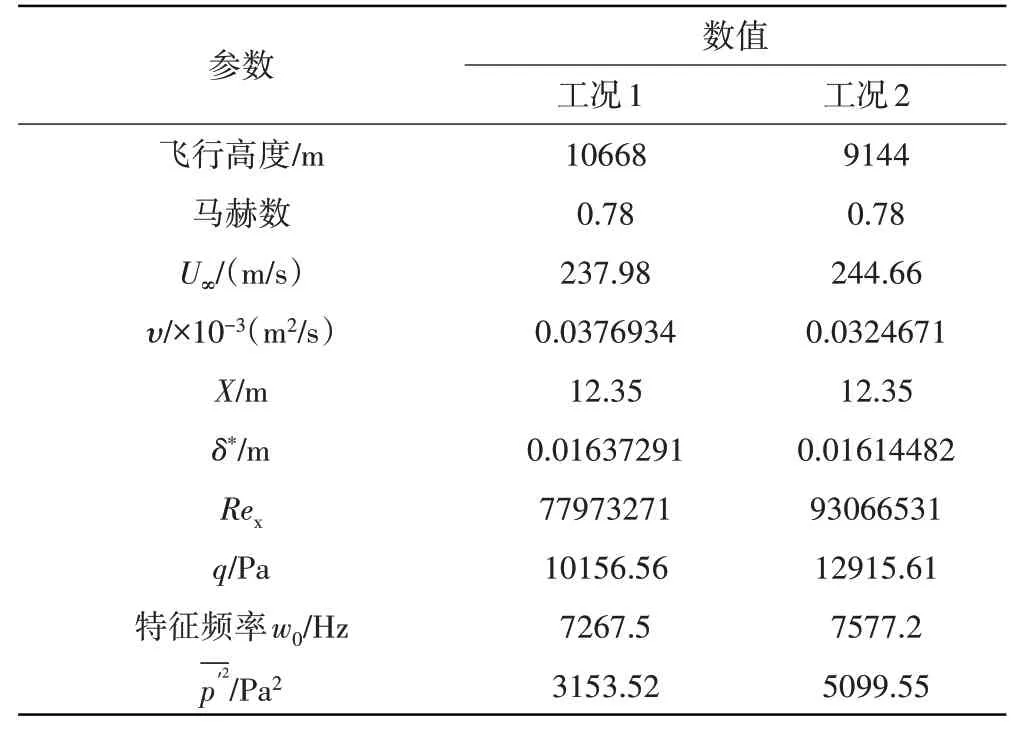
表1 Robertson模型计算参数

在工况1、2下Robertson模型的计算结果与试验结果分离得到的1/3倍频程谱对比如图8所示。从图中可见，在中心频率为20~10000 Hz时，二者结果较为接近，最大相差约2 dB。频率较高时，试验结果分离得到的湍流边界层噪声衰减程度要大于Robertson模型的计算结果。

图8 1号传感器试验和Robertson模型计算结果对比

计算表明在总声压级上二者结果接近，相差约2 dB。结果见表2。

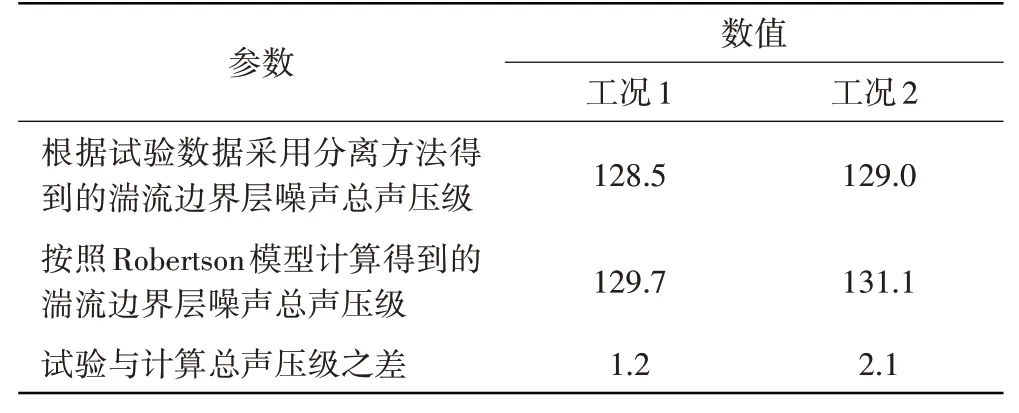
表2 总声压级对比 dB

5 结论

（1）采用分离技术得到的湍流边界层噪声与Robertson模型计算结果相比，总声压级相差约2 dB。在中心频率为20~10000 Hz时，利用分离技术得到的湍流边界层噪声与Robertson模型计算的1/3倍频程谱较为相近；

（2）在典型巡航状态下湍流边界层噪声的贡献量要大于发动机噪声的。