基于风-储联合的双层频率响应控制策略
杨伟峰,文云峰,张武其,邓步青
(湖南大学电气与信息工程学院,湖南省长沙市 410082)
0 引言
近年来,由于全球化石能源价格上涨、环境治理力度加强,新能源机组被大规模建设和投运,能源清洁化程度不断提高[1-2]。但由于大部分风机需经变流器并网,发电机转子与系统频率解耦,导致在风电大规模并入电网后电网的惯量水平与调频能力大幅下降,影响系统频率稳定性[3]。虚拟惯量、有功下垂、功率参考等风机调频控制策略成为研究热点,基于上述策略,风机出力可响应并抑制系统频率变化趋势[4-6]。为改善高风电渗透率电力系统的频率稳定性,中国电网运营商已开始要求风电场具备一定调频能力[7]。但由于风能波动性受风机转速保护模块的约束,风电调频能力十分有限且存在不确定性,有时难以达到预期调频效果[8]。
电池储能具有响应速度快、控制灵活、出力稳定的特点,为弥补和提升风电调频能力提供可行性[9]。一些学者已针对含储能的风电场结构,提出了风-储设备协同调频控制策略[10-11]。其中,文献[10]基于有限状态机控制结构,提出一种风-储辅助调频控制策略,其可通过协调风-储出力,在满足系统调频需求的同时,优化储能荷电状态(SOC),延长其使用寿命。文献[11]则根据最优控制原理提出一种风电场分层惯量控制策略,推导了风-储出力与风能损失成本、储能老化成本间的解析关系,并以成本最低为目标确定风-储设备出力参考。
然而,上述两种优化策略均仅针对风电场内的风-储设备,由于场内储能容量通常较小,即便风电场配有储能,其调频能力仍非常有限。随着储能成本降低和风电渗透率的进一步提升,目前有许多电网已开始投建兆瓦级储能电站直接参与调频[12]。由于各场站运行状态不同,其调频性能与成本存在差异,为此一些学者已提出相关控制策略用于协调风-储场站间的调频出力。文献[13]根据风机运行特性将风速分区,并在各区中设置对应风-储场站协调策略,使风电场可在多种风况下参与调频,但未对调频成本进行量化,控制缺乏最优性。文献[14]基于模型预测控制提出一种风-储场站联合调频控制策略,其可根据系统状态确定各场站出力最优值,在最小化风-储有功动作总量的同时,得到最佳调频效果,但仍未考虑设备调频时所产生的各类成本。此外,风电场参与调频时机组出力变化与场内尾流波动也将引起风机疲劳载荷增加,加速其材料缺陷积累,影响设备使用寿命[15-16]。但在目前已有的风电场载荷优化策略中,仅量化了由风机出力变化所引起的载荷部分,并未考虑因场内上游机组出力变化导致尾流波动在下游机组上产生的载荷增量,故对风电场内载荷的实际优化效果有所影响[17-19]。
针对上述问题,本文基于风-储场站提出一种双层频率响应控制策略,通过协调风-储场站间与场内风机间的出力,在满足系统调频需求的同时,降低场站调频总成本及场内载荷总量。首先,分析并量化各场站调频时的内损、老化与风险成本,并在场站协调层上建立场站有功分配控制策略,确定成本最低的场站调频方案。然后,基于风机出力与尾流、载荷间的线性关系,结合和增积减(additive increase multiplicative decrease,AIMD)算法在机组协调层上建立风电场分散式有功控制策略,协调风机间出力,在维持风电场调频性能的同时,降低场内载荷总量。最后,在Simulink 中构建含2 个100×5 MW 双馈风电场和2 个100 MW/100 MW·h 锂电池储能设备的IEEE RTS-79 系统,验证本文所提策略的有效性。
1 双层频率响应控制架构
本文所提出的双层频率响应控制架构如图1 所示。图1 中:PBES,refk为储能有功出力参考值;Ri,z为风机尾流干涉矢量,其具体结构见附录A 式(A1);下标k表示储能电站序号;下标i表示风电场序号;下标z表示风机序号,共N台风机。
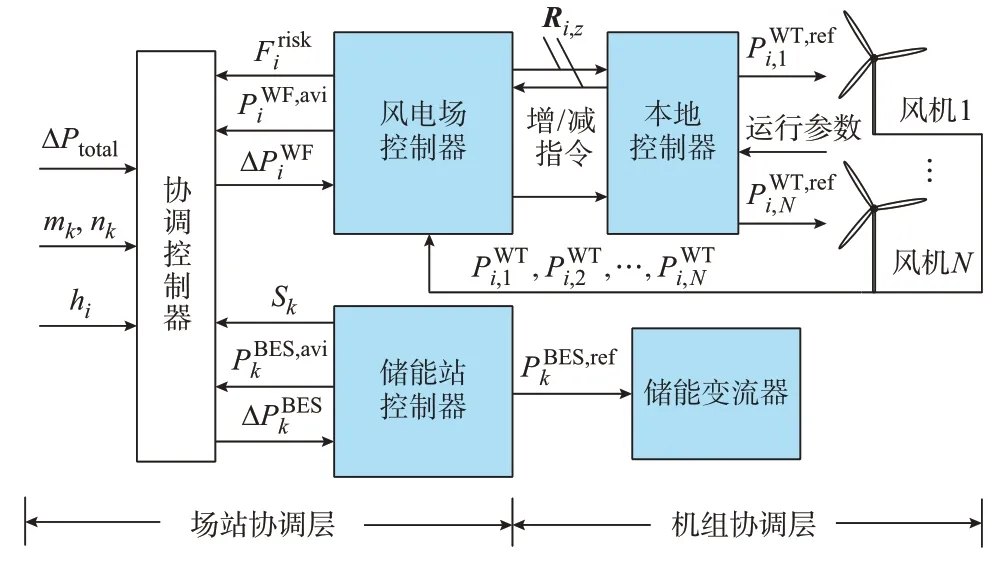
图1 双层频率响应控制策略结构Fig.1 Structure of control strategy for bi-level frequency response
在场站协调层中,协调控制器可根据本地调频策略计算有功参考值ΔPtotal来确定其所控风-储场站的调频动作总量。同时,在各控制周期内协调控制器还将根据风电场和储能电站上传的参数(备用风险Friski、荷电状态Sk、风电场备用容量PWF,avii、储能备用容量PBES,avik),结合内损功率系数mk、nk、hi,评估不同设备调频时的内损、老化与风险单位成本,以确定成本最低的场站调频出力方案。最后,再由协调控制器将求得的储能调频参考值ΔPBESk和风电场调频参考值ΔPWFi下发至各场站控制器。其中,有功参考值ΔPtotal可由式(1)计算得到[20]。
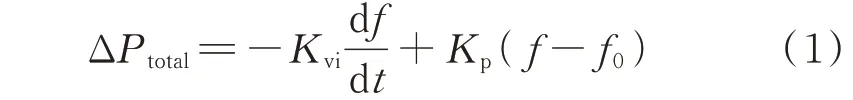
式中:Kvi为惯量响应系数;f为系统频率;Kp为一次调频系数;f0为额定频率。
在机组协调层中,当各风电场控制器接收到调频参考值ΔPWFi后,场内风机的调频出力参考值PWT,refi,z则将基于由AIMD 算法构建的分散式有功控制策略计算得到。该策略通过计算场站实际调频出力与参考值间的偏差,确定场站控制器下发的出力增/减方向指令。接着,由风机本地控制器响应该方向指令,根据AIMD 算法中的参数、机组运行状态、尾流状态,求得各机有功出力参考值PWT,refi,z。同时,在下一轮周期内,根据风机出力PWTi,z重新计算并更新风机调频出力参考值,确保风电场调频出力。由于本文将储能电站视为单个机组展开研究,其在接收命令ΔPBESk后将跳过站内协调优化过程直接调节设备出力。
基于该双层频率响应控制架构,在风-储场站参与调频过程中,协调控制器中的场站有功分配控制策略可根据各场站运行状态,在满足系统调频需求的同时,降低由内损、老化、风险因素产生的调频总成本。同时,基于机组协调层中的分散式有功控制策略,风电场可在维持其调频能力的同时,通过场内风机间的出力协调,降低该过程中场内产生的疲劳载荷总量。
2 场站有功分配控制策略
场站有功分配控制策略的目标是通过协调风-储场站出力,在满足电网调频需求的同时,控制调频成本最低。场站有功分配控制策略流程见图2。
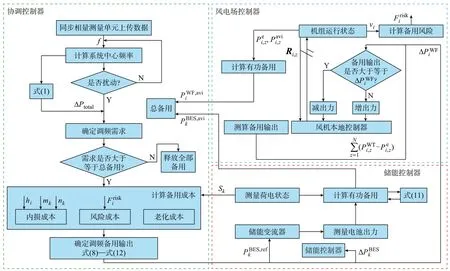
图2 场站有功分配控制策略Fig.2 Control strategy of active power distribution in stations
在电网出现有功扰动后,协调控制器将根据有功参考值ΔPtotal确定场站调频总出力需求。接着,该协调控制器会比较风-储备用总量与调频需求总量间的大小,以判断是否有必要协调风-储场站出力。若备用总量大于需求值,协调控制器将基于由内损、风险与老化成本因素构建的出力优化模型,计算得到总成本最低的风-储场站调频出力方案;否则,释放全部风-储备用。场站调频成本计算与优化模型构建的详细过程如下。
2.1 场站出力成本
风-储场站出力携有不同成本特征,为使二者设备参与调频时所产生的总成本最低,需根据风-储设备实际运行状态对其出力进行协调。风-储场站出力成本主要包括:由设备内耗产生的设备内损成本、由风能波动因素形成的备用风险成本及电池SOC引起的储能老化成本。
2.1.1 设备内损成本
当储能参与调频时,因出力上升而新增的内部功率损耗是一个不可忽视的因素,将影响储能设备的充放电效率与调频效果。为考虑储能电站调频时由内损因素引起的负面影响,量化储能备用释放时的内损成本,本文基于文献[21]中由长周期运行场景所得的储能出力与内损功率间的解析关系,建立储能内损成本CBES,lossk量化模型:

式中:Closs为单位内损成本;Tu为场站有功分配控制策略的控制周期;mk和nk为储能内损功率系数,与储能SOC 相关,并在给定的SOC 范围内有对应常数值[22]。
与储能内损类似,当风电场出力增加时,由于其场内集电线路及设备电流升高,也将增加一定有功损耗。为量化风电场调频过程中的内损成本,本文基于文献[23]中风电场出力与损耗功率间的解析关系,建立风电场内损成本CWF,lossi量化模型:
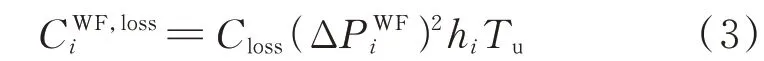
式中:hi为风电场内损功率系数,与风电场内设备与集电线路上的阻值相关。
2.1.2 备用风险成本
与储能相对稳定的有功备用不同,受风能波动特性影响,风电场可能在调频过程中出现有功备用不足预期的问题。为在协调场站出力时兼顾风电备用不确定性因素,本文提出一种备用风险成本模型,量化风电场调频备用的风险成本。首先,为表征不同风况下风电场调频备用不足的概率,通过风电场每个控制周期前10 min 区间内的测风数据滚动拟合为适于短时间尺度的七参数威布尔分布概率函数f(vi)[24]:a a

接着,基于式(4)对风速vi进行0 至风机额定风速Vrate积分,求得该风电场有功备用不足的概率F:
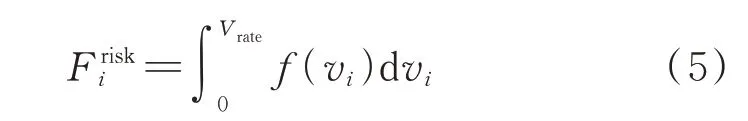
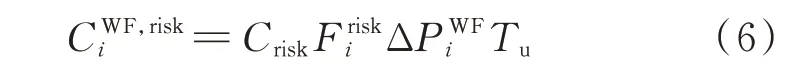
储能电站则出力稳定无须考虑其备用风险成本。
2.1.3 储能老化成本
由于SOC 对储能设备老化有较大影响,故本文引入文献[25]中根据储能长周期运行数据建立的储能老化成本C量化模型,见式(7)。
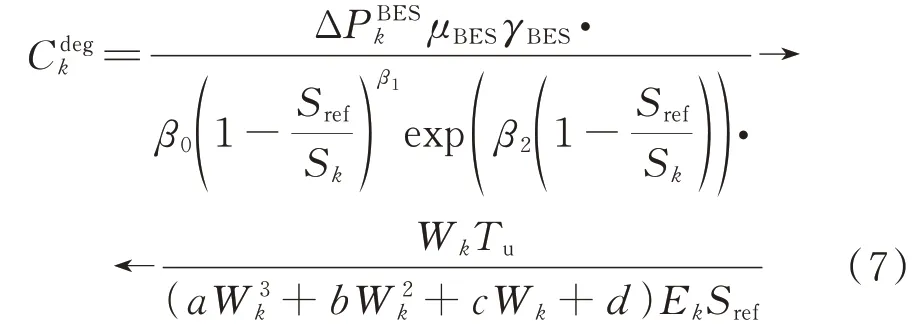
式中:μBES为储能设备投资成本;γBES为储能设备额定循环寿命;Sref为SOC 参考值;Wk为环境温度;Ek为储能容量;β0、β1、β2为依赖于SOC 的循环寿命系数;a、b、c、d为依赖于温度的循环寿命系数。
2.2 场站有功分配优化模型
基于上述3 类出力成本模型,建立场站有功分配优化模型,其可通过协调场站间出力,在场站满足调频需求与运行约束的同时,降低该调频过程总成本。场站有功分配优化模型如下:

式中:Smax和Smin分别为储能SOC 的最大和最小约束;P为储能实际有功出力。
式(8)为场站有功分配优化模型的目标函数;式(9)与式(10)则分别为风电场和储能的调频备用容量约束,该约束通过测算各场站当前的最大出力能力与实际出力得到;储能调频备用除受最大出力约束外,还将受到SOC 限制,见式(11)。另外,为保证风-储场站整体调频效果,在场站协调层各控制周期内由协调控制器得到的场站调频参考值ΔP、ΔPWFi的总和须满足系统调频需求ΔPtotal,见式(12)。
3 机组协调层风电场分散式有功控制策略
在协调控制器下发场站出力命令后,储能电站将直接以ΔPBESk为目标调节出力。风电场控制器则会在接收ΔPWFi后,再次分配该调频命令,发送至各风机本地控制器中具体执行。考虑到风电场调频过程会引起风机上疲劳载荷量增加,影响机组的使用寿命,本文基于AIMD 算法提出一种含尾流与载荷因素的风电场分散式有功控制策略。其可通过风机间出力的协调,在维持风电场调频性能的同时,有效降低风电场内的疲劳载荷总量。本章首先根据风机出力、尾流波动与载荷间的线性解析关系,建立风电场有功控制模型。接着,基于该模型与AIMD 算法结构,构建风电场分散式有功控制策略。
3.1 考虑尾流与载荷的风电场有功控制模型
在风电场调频过程中,风机有功出力变化将引起其传动轴形变扭矩Ts与塔筒弯矩MT两类疲劳载荷量增加,影响机组安全运行[26]。
基于文献[27]中由风机动力学模型、风电场尾流模型所推导的风机出力、尾流波动与两类疲劳载荷间的解析关系,本文构建含载荷与尾流因素的风机离散状态空间方程:

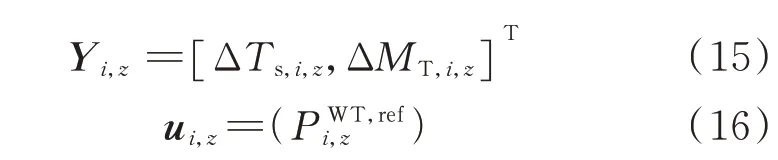
式中:ΔTs,i,z和ΔMT,i,z为疲劳载荷量。
由式(13)可计算风机在不同运行状态下,其调频出力将产生的疲劳载荷量ΔTs,i,z和ΔMT,i,z。假设此时风电场共有N台风机,则风电场的状态空间方程可被描述为:

接着,根据式(17)构建以风电场疲劳载荷最小为目标的有功控制模型。其中,目标函数为:

式中:QT和QM为载荷权重。

3.2 基于AIMD 算法的风电场分散式有功控制策略
在风电场控制器收集机组运行参数后,其可基于式(19)转化的有功控制模型集中求解场内各风机调频出力参考,减小场内疲劳载荷总量。然而,随着机组数量上升,该模型将会包含高维矩阵与矢量,造成风电场控制器计算负担的增加。
AIMD 算法是一种反馈控制算法,该算法通过多个代理以一种平缓方式探索可用资源,直到超过需求资源总量时,向它们发送一个拥塞通知,要求减少资源,并等待探索环节的重启。由于其具有动态优化能力且可基于多个代理进行同步计算,目前已被广泛用于解决互联网拥塞与分散协调优化等问题[28]。该算法没有迭代过程,每当下层代理求得自身优化量后会被即刻执行,并在下轮周期中由上层代理对系统的输出与需求关系进行判断和校正。故与传统的目标级联分析与交替乘子算法等分布式算法相比,该算法计算量更小,控制过程更简洁,更适用于对控制实时性有很高要求的风电场有功控制场景[29]。另外,由文献[30]中的AIMD 算法长期优化收敛理论可知,基于AIMD 算法计算得到的最优解会向集中优化策略最优解收敛。
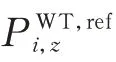
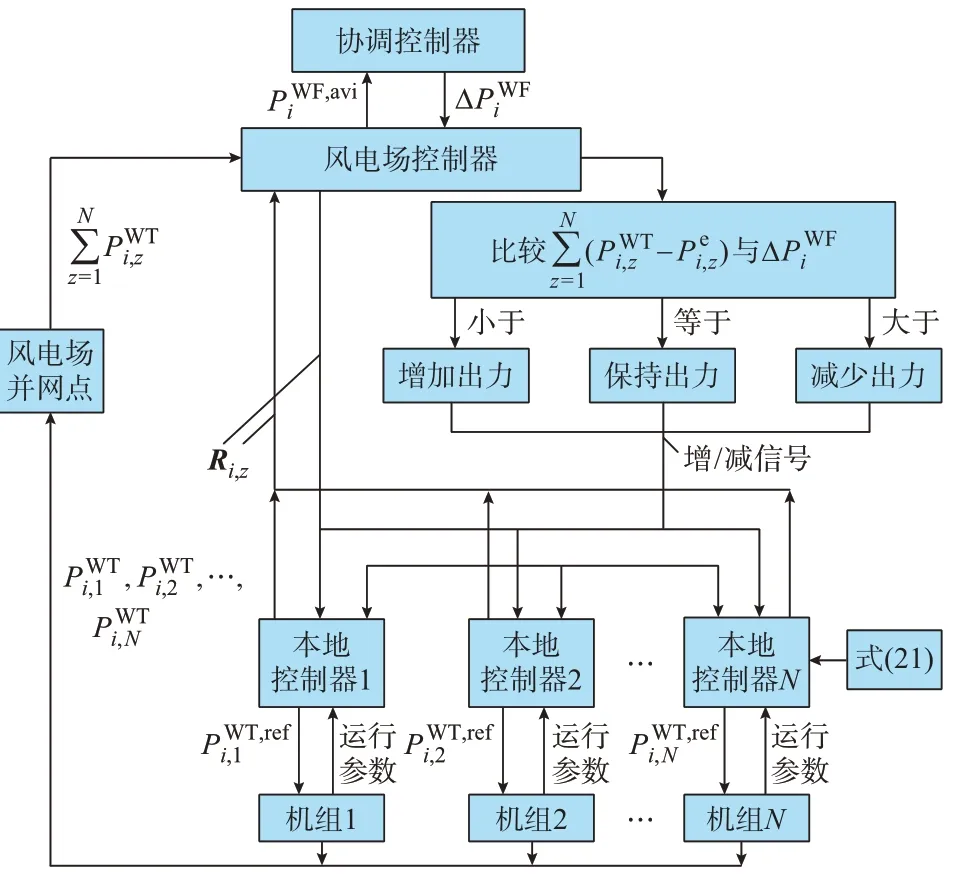
图3 风电场分散式有功控制策略Fig.3 Decentralized active power control strategy for wind farms

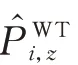
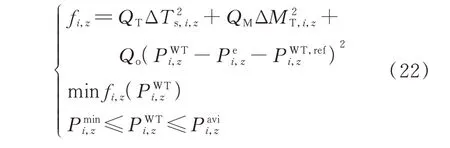
式中:Qo为机组出力权重。
由式(22)可知,由于风机运行状态不同,各风机调频出力与载荷间的解析关系存在差异,使得本地控制器在相同调频参考值P,ref下执行的调频出力P并不一致,即对载荷影响较小的机组,其调频出力P-P可更接近于参考值P,ref,进而起到协调机组出力、降低场内疲劳载荷总量的效果。由式(21)可知,对于调频会产生较大疲劳载荷的机组,其会被优先减少出力,也可降低场内载荷总量。另外,由于在该分散式有功控制策略中,风电场控制器仅需判别实际调频出力与调频出力命令间的等式关系,计算量较小,故可选用较短控制周期。
4 算例验证
4.1 测试系统
由于风电出力的不稳定性,电网公司要求按照风电场装机容量的10%~20%配套投入储能电站或储能设备,用于满足其调峰、调频能力需求。基于该背景,本文在Simulink 中搭建IEEE RTS-79 测试系统,并接入2 个100×5 MW 双馈风电场及2 个100 MW/100 MW·h 锂电池储能电站,用于验证所提双层频率响应控制策略的有效性。该测试系统结构见附录B 图B1。为便于风电场建模,场内每25 台风机将被视为一个机群,故每个风电场拥有WT1至WT4这4 个机群。其中,WT1、WT2为上游机群,WT3、WT4为下游机群,且各机群风况条件不一致。场站有功分配控制策略与风电场分散式有功控制策略中的主要参数见附录B 表B1 和表B2。
4.2 场站协调层控制效果
该测试系统仿真时长共100 s,在系统发生有功扰动前,2 个风电场均恒定出力,系统频率维持在50 Hz。当仿真至10 s 时,Bus121 母线因故障退出运行,并造成395 MW 约系统总容量9%的有功缺额,引起系统频率跌落,双层频率响应控制策略被触发。在该故障发生时刻,储能电站BES1与BES2调频备用容量均为100 MW,风电场WF1和WF2调频备用容量均为50 MW;BES1与BES2的SOC 分别为30%与60%。
为验证场站有功分配控制策略对风-储场站调频出力成本所起到的优化作用,本文分别基于相同系统运行状况与不同成本因素分配系统调频需求ΔPtotal。不同成本因素下风-储场站的调频出力见图4。其中,图4(a)为场站有功分配控制策略在考虑内损、风险、老化3 类成本因素时确定的调频方案。相比图4(b)中不考虑老化成本时的出力方案,其可通过抑制BES2的出力,将BES2上的部分调频任务分配至WF1与BES1中,减少由于BES2的SOC 过低所产生的老化成本;与图4(c)中不考虑内损成本的出力方案相比,则可通过减少WF1与BES1出力,将调频任务转移到BES2上,减少WF1与BES1所引起的高昂内损成本;与图4(d)中不考虑风险成本的出力方案相比,可通过减少WF1与WF2出力,降低因风电出力不稳定所产生的风险成本。另外,由图4(a)至(d)可见,当WF2在一段时间内受风速影响出力低于预期并造成有功缺额时,该场站有功分配控制策略可及时协调其余几个场站出力补足。
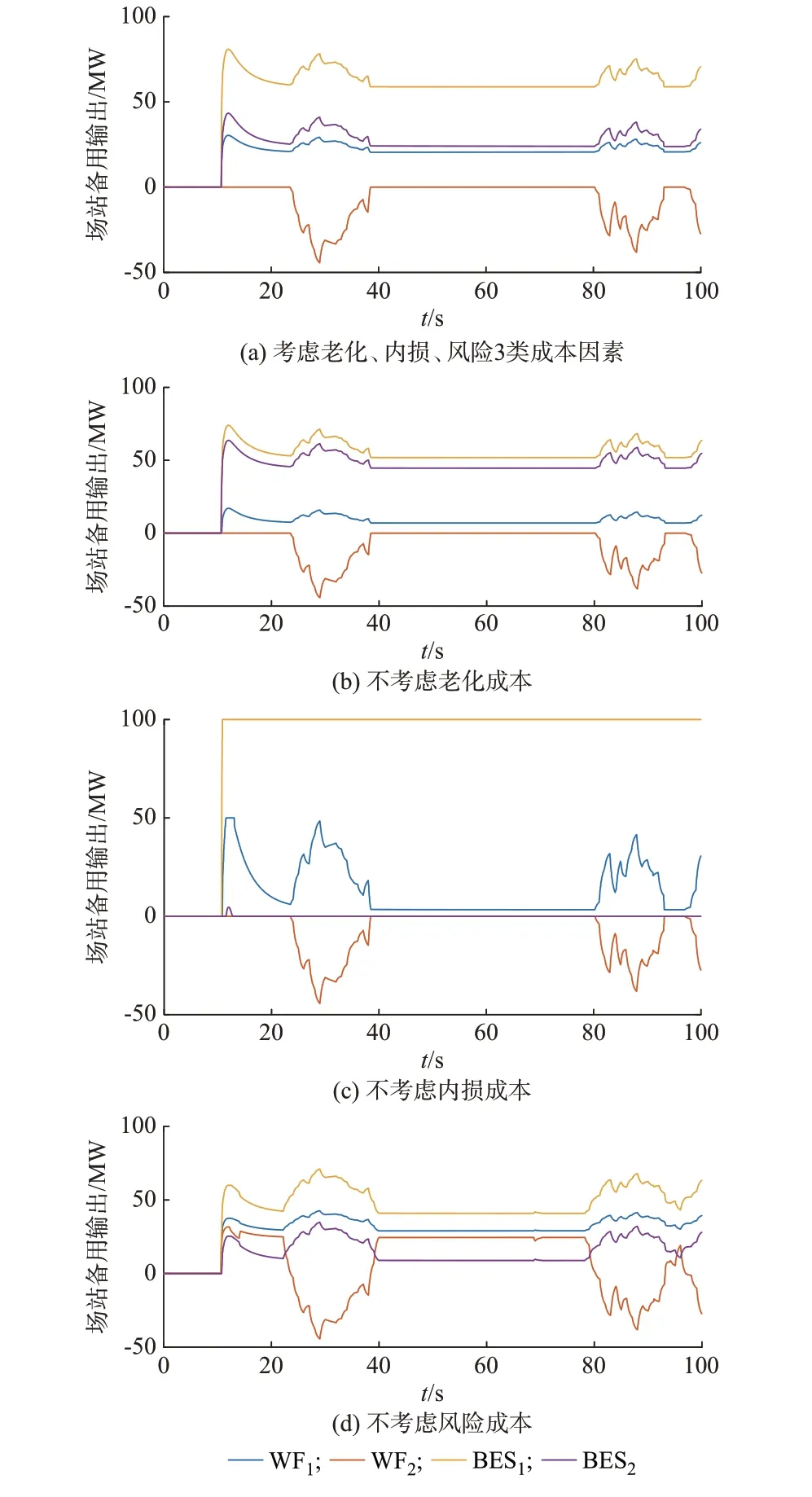
图4 基于不同成本因素的风-储场站调频出力Fig.4 Frequency regulation output of wind farms and energy storage stations based on different cost factors
由于本文在构建场站有功分配控制策略时,将各场站调频出力参考总和须等于协调控制器中调频出力命令作为约束条件,故即使在不同类型成本因素组合下,该场站有功分配策略均可维持系统调频性能,改善系统频率最低点及准稳态频率,具体见附录B 图B2。
由附录B 图B3 可知,当该场站有功分配控制策略同时包含老化、内损、风险3 类成本时,其给定的调频方案总成本与不考虑老化、内损、风险成本的策略相比,则可分别下降5.9%、28.0%与14.2%,说明该控制策略可在维持风-储场站整体调频性能的同时,有效降低风-储调频过程中各类成本总和。
4.3 机组协调层控制效果
为体现风电场分散式有功控制策略的调频与载荷优化能力,本文以3 种成本因素下WF1的调频方案作为参考,基于相同风况条件,根据比例、集中式、分散式有功控制策略分别对WF1进行调频出力控制。其中,集中式有功控制策略的控制周期因风电场控制器计算能力约束而设为0.5 s,而比例与分散式有功控制策略则由于其结构逻辑更为简单、计算压力小,其二者控制周期设为0.1 s。
风电场WF1在比例、集中式、分散式有功控制策略下各机群的有功出力情况见图5。

图5 基于比例、集中、分散式有功控制策略的风电场WF1各机群有功出力情况Fig.5 Active power output situations of each unit group with proportional,centralized and decentralized active power control strategies in wind farm WF1
由于场内风况较好,各机群出力均具备满发能力,使得该风电场在按比例有功控制策略释放机组有功备用参与调频时,各机群出力水平基本一致,见图5(a)。而风电场在集中式与分散式有功控制策略下参与调频时,则可根据机群运行状况,量化因风机出力变化所引起的疲劳损失,并通过各机群间出力的协调,在维持场站调频性能的同时,降低场内疲劳载荷总量。但由于分散式与集中式有功控制策略相比,前者调校机群出力的频率更高,故可控制机群实际出力更接近最佳值,以得到更好的载荷优化效果,见图5(b)和(c)。同样,由于分散式有功控制策略的控制周期更短,可更频繁地更新风电场站调频备用参考值,使得其与集中式有功控制策略相比,可控制风电场调频出力更接近场站协调控制器下发的出力参考值ΔPWFi,具体见附录B 图B4。
由图5(a)至(c)可知,在分散式和集中式有功控制策略作用下,风电场WF1为降低由上游机群WT1和WT2尾流风速变化所造成的疲劳载荷部分会减少上游机群有功变化幅度,但同时也会考虑下游机群WT3与WT4因有功出力变化所引起的疲劳载荷而分担部分调频任务给上游机群,并基于4 个机群实时运行状况和风况,在风电场各控制周期内协调机群间出力,进而降低场内疲劳载荷总量。为进一步对比各类有功控制策略下风电场所产生的疲劳载荷量,本文依据仿真10~100 s 间各风机的MT和Ts数据进行等效疲劳载荷计算与雨流循环计数分析。基于3 种策略的MT和Ts等效疲劳载荷计算结果见表1 和表2。
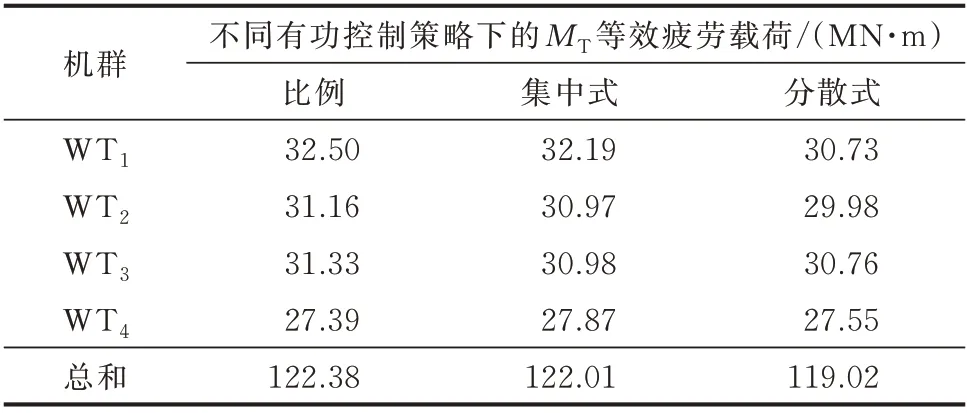
表1 风电场WF1中MT 等效疲劳载荷Table 1 Equivalent fatigue load of MT in wind farm WF1

表2 风电场WF1中Ts 等效疲劳载荷Table 2 Equivalent fatigue load of Ts in wind farm WF1
由表1 可知,相比比例有功控制策略,所提分散式有功控制策略可通过各机群间出力的协调,在维持与减小下游机群WT3和WT4上MT载荷的同时,有效减少因上游机群WT1和WT2出力变化所引起的MT载荷,进而降低WF1调频过程中场内MT载荷总量的2.75%。而相比集中式有功控制策略,该分散式有功控制策略则基于其具有控制周期短、响应速度快的优势,进一步提升载荷优化效果,降低场内MT载荷总量的2.45%。在该分散式有功控制策略作用下,WF1中机群WT1上的MT载荷优化效果最为明显,相比比例、集中式有功控制策略分别可下降5.72%、4.51%。
各控制策略下机群WT1上MT的时域曲线和雨流循环计数结果如图6 所示。由图6(a)可知,在10~70 s 时段,相较于比例与集中式有功控制策略,分散式有功控制策略可有效减缓机群MT载荷大小。由图6(b)所示机群WT1的MT雨流循环计数结果可知,虽然基于分散式有功控制策略下机群WT1上MT的雨流循环次数不发生改变,但MT的变化幅度下降明显,说明该分散式有功控制策略对塔筒弯矩MT具有优化疲劳载荷的作用。

图6 风电场WF1中机群WT1的塔筒弯矩MTFig.6 Tower bending moment MT of unit group WT1 in wind farm WF1
同理,由表2 可知,相比比例、集中式有功控制策略,所提分散式有功控制策略则可有效降低WF1内Ts载荷总量的3.23%与2.59%。其中,对WF1中机群WT1的优化效果最为明显,与比例、集中式有功控制策略相比可下降6.94%、4.61%。
各控制策略下机群WT1上Ts的时域曲线与雨流循环计数结果见图7。由图7(a)可见,基于分散式有功控制策略下机群WT1上的Ts变化幅度在10~100 s 时段下降明显,这说明机群WT1等效疲劳载荷有所减少。同样,根据图7(b)所示机群WT1上的Ts雨流循环计数结果可知,虽然基于分散式有功控制策略下机群WT1的Ts雨流循环次数也不发生改变,但Ts的变化幅度也有明显下降,故也可说明该分散式有功控制策略对传动轴扭矩Ts具有优化疲劳载荷的作用。
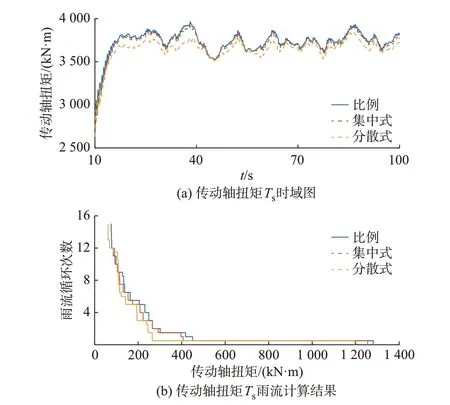
图7 风电场WF1中机群WT1的传动轴扭矩TsFig.7 Drive shaft torsion torque Ts of unit group WT1 in wind farm WF1
为说明该分散式有功控制策略在风电场备用不稳定时仍可起到优化载荷的作用,在此以不考虑风险成本因素时WF2的调频方案作为参考,对WF2内的MT与Ts载荷进行分析。由附录B 表B3 和表B4可知,在分散式有功控制策略下,相比比例、集中式有功控制策略,WF2中MT等效疲劳载荷可下降1.97%、1.03%,WF2中Ts等效疲劳载荷可下降5.92%、4.69%,可说明该有功控制策略在风电场调频备用不稳定场景下仍可起到有效的载荷优化作用。
5 结语
本文提出了一种双层频率响应控制策略用于协调多个风-储场站间及风机间的调频出力。首先,分析并量化各场站调频时的内损、老化与风险成本,在场站协调层上建立场站有功分配控制策略,确定成本最低的场站出力方案。然后,基于风机出力与尾流波动、疲劳载荷间的线性关系,结合AIMD 算法建立风电场分散式有功控制策略,在维持风电场调频性能的同时,降低场内疲劳载荷总量。
仿真结果表明,当采用所提策略后,风-储场站可在维持系统频率稳定性的同时,有效减少场站调频成本;风电场可在维持调频性能的同时,有效减少场内疲劳载荷总量。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

