基于变分有限元法的调蓄水库渗流稳定性分析

姚 震

（甘肃省水利水电勘测设计研究院有限责任公司,甘肃 兰州 730030）

1 引言

调蓄水库是引水工程的重要建筑物,在工程效益中发挥着举足轻重的作用,但在地震作用中容易出现渗漏、失稳等地质问题,土石坝渗流稳定性分析一直是工程界学者们关注的焦点。吕远坤.建立大坝流固耦合模型进行渗流稳定性分析[1],李志峰等人通过渗流有限元计算分析,评价了眠羊地水库大坝的渗流安全稳定[2]；随着现代信息化软件的介入FLAC 3D[3]、Geostudio[4]、ANSYS[5]使得渗流稳定性计算更便捷高效准确,更为直观的是数值模拟在土坝渗流稳定分析中的应用[6-8],常用的渗流稳定计算方法有有限元法[9-10],有限元的重要理论是变分原理和加权余量法,都是将微分方程离散求解,具有善于处理复杂区域和边界条件的优点,本文通过建立二维变分有限元模型,处理渗流微分方程的定解条件,开展校核水位和正常蓄水位情况下坝体渗流稳定计算,采用刚体极限平衡法综合考虑平面应变问题、滑动面及土条间法向作用力问题开展校核水位、正常蓄水位和地震作用下的坝坡稳定分析。

2 渗流稳定性分析方法

2.1 渗流有限元分析原理

2.1.1 二维渗流基本方程

对不可压缩流体,且域内无体积源时,根据达西定律在各向异性介质中,有：

代入式（1）,则得稳定渗流的微分方程式：

式中：h 为水头函数；kxx、kxy分别为主渗透系数kx在x、方kyy向上的投影；、分别为主渗透系数ky在x、y 方向上的投影。

2.1.2 渗流基本微分方程的定解条件

渗流场的计算分析考虑二维稳定渗流问题,故在考虑定解条件时,只需要考虑第一类和第二类边界条件。

（1）第一类边界条件（水头边界条件）：

当渗流区域的某一部分边界（如Γ1）上的水头为已知时,边界条件为：

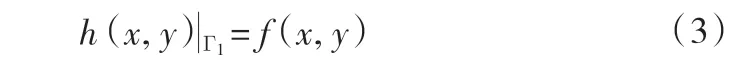
式中：Γ1为第一类边界；h 为水头函数；f（x,y）为已知水头。

（2）第二类边界条件（流量边界条件）：

当渗流区域的某一部分边界（如Γ2）上的法向流速已知时,边界条件为：

考虑到各向异性时为：

式中：Γ2为第二类边界；n 为Γ2的外法线方向；q0为已知流量。

2.2 变分有限元法

由变分原理,上述模型的求解等价于下列泛函I（h）的极值问题,即：

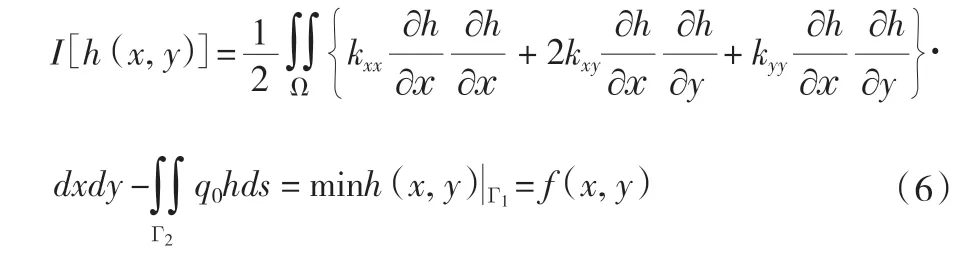
对渗流场所有单元的泛函求得微分后叠加,并利用I（h）极小值的条件,有：

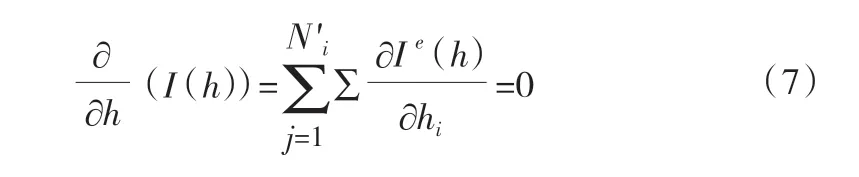
式中：[K]为整体劲度矩阵；{h}为未知节点水头值构成的列向量；{Q }为已知项。

2.3 稳定性分析方法

坝坡抗滑稳定计算应采用刚体极限平衡法。对于均质坝,采用条块间作用力的简化毕肖普法或摩根斯顿-普赖斯法。毕肖普给出的坝坡稳定分析的简化方法考虑了土条间的法向力,但不考虑土条间剪切力,主要考虑三大问题：（1）分析研究的对象都是平面应变问题；（2）滑动面仍然采用的圆弧滑裂面；（3）土条间考虑法向作用力,但切向作用力简化不计。

对于剪切面进行极限平衡分析可知：

综合考虑水平位置上的作用力平衡条件可得：

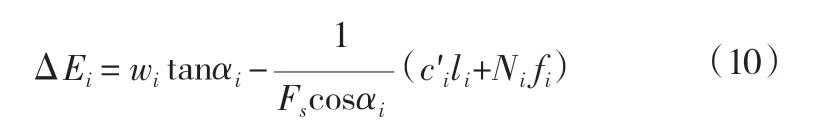
式中：ΔEi物理意义是作用在各个土条间的法向力的增量,把作用在滑动面上全部土条的ΔEi进行求和,ΔEi=0。

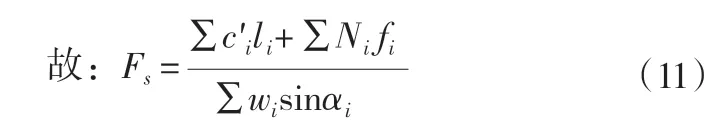
竖直方向作用力的和为0,即∑Yi=0,可得：

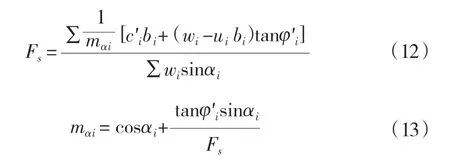
3 工程简介

引洮（博）济合供水工程调蓄水库地处甘南高原中低山丘陵沟壑区,现代侵蚀强烈,植被发育良好,水库区两岸山脊海拔大都在3060 m～3080 m 之间,库区主沟道为海螺沟,调蓄水库总库容68 万m3,工程等别为Ⅲ等,工程规模为中型,调蓄水库和水厂等主要建筑物为3 级,次要建筑物为4 级,其余临时性建筑物均为5 级。主要建筑物按50 年一遇洪水设计,按1000 年一遇洪水校核。本工程建筑物抗震设防烈度为7 度。

4 调蓄水库模型构建

4.1 模型构建及网格划分

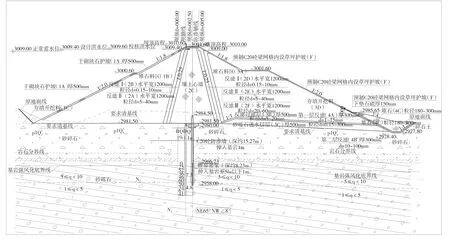
图1 复合土工布防渗心墙堆石坝剖面图（坝横0+419.87）

以调蓄水库最大剖面（坝横0+419.87 断面）即标准断面作为该壤土心墙堆石坝渗流计算的典型断面。模型上、下游长度取约2 倍的坝高；基础深度范围从建基面向下取1 倍坝高。模型包括了可能影响计算域渗流场的主要边界范围,模拟壤土心墙堆石坝坝体和坝基及排水、帷幕等。模型边界条件设置如下：甘南调蓄水库壤土心墙堆石坝渗流场的模拟,主要考虑以下边界条件：基础底部和模型上下游边界视为不透水边界；水位面以下的河床均视为已知水头边界；位于河床以上地表,均按可能逸出面处理,但实际逸出面通过计算分析,经迭代确定,模型离散后的有限元计算网格有结点8823 个,单元有8887 个。

图2 调蓄水库最大截面二维有限元网格图

4.2 模型参数及计算工况

坝体、坝基以及各分区材料渗透系数见表1。

表1 渗流分析各材料分区模型参数

（1）渗流计算应考虑水库运行中出现的最不利条件,选取以下两种水位组合情况：

工况I：上游校核水位：3009.60 m；下游相应水位：2985.65 m。

工况II：上游正常蓄水位：3009.00 m；下游相应水位：2985.65 m。

（2）坝坡稳定性计算工况

土石坝施工、建成、蓄水、库水位降落和地震期的各个时期。受到不同的荷载,土体也具有不同的抗剪强度,应分别计算其抗滑稳定性。控制抗滑稳定的有施工期（包括竣工时）、稳定渗流期、水库水位降落期和正常运用遇地震四种工况,本项目计算内容如下：

工况I：（校核水位坝坡稳定）上游校核洪水位：3009.60 m,下游相应水位：2985.65 m。

工况II：（正常水位坝坡稳定）上游正常蓄水位3009.00 m,下游相应水位：2985.65 m。

工况III：正常蓄水位（3009.00 m）+地震,依据国家地震局1：400 万2001 年版《中国地震动参数区划图》（GB 18306-2001）,工程区地震动峰值加速度为0.10 g,相应的地震基本烈度为Ⅶ度,地震动反应谱特征周期为0.45 s。

5 计算结果分析

5.1 渗流场

经过两种工况下的渗流场计算,绘制工况I、II 下大坝典型断面水头分布图,见图3、图4。

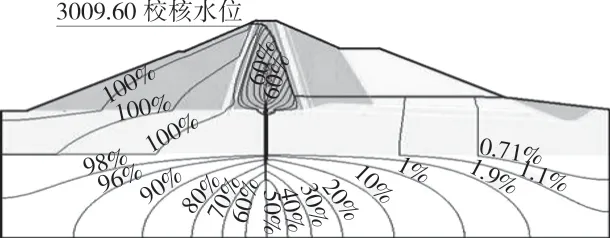
图3 工况I 校核水位下标准断面水头等值线图

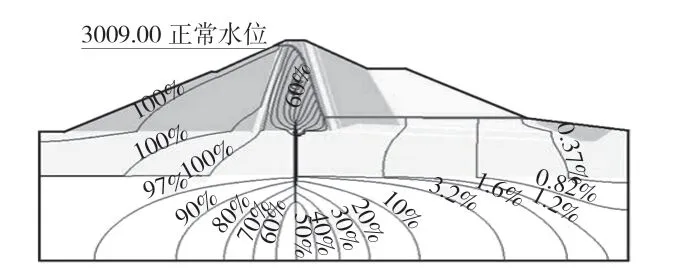
图4 工况II 正常水位下标准断面水头等值线图

经过防渗体时,浸润线明显降低,两种工况下坝体浸润线分布符合一般壤土心墙堆石坝规律,断面下游浸润线基本水平,起到了较好的排渗效果。

标准断面在校核洪水位和正常蓄水位下的截面单宽流量分别为2.136 m3/d 和2.052 m3/d,符合实际情况。

表2 截面流量统计表 单位：m3/（d·m）

5.2 坝坡稳定性分析

根据坝坡稳定性计算原理,分析3 种工况下的上下游坝坡滑动面,见图5～图7。

图5 校核水位下上下游坝坡滑动面

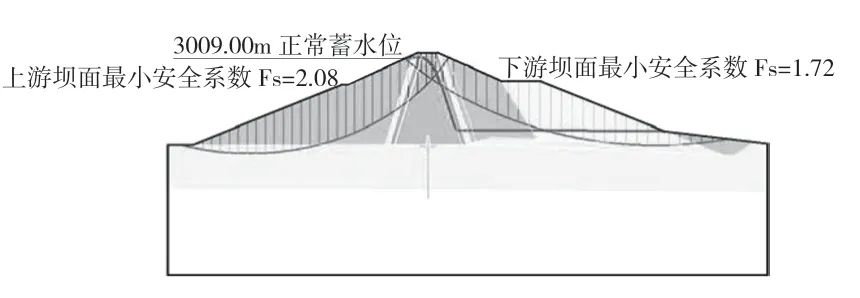
图6 正常水位下上下游坝坡滑动面

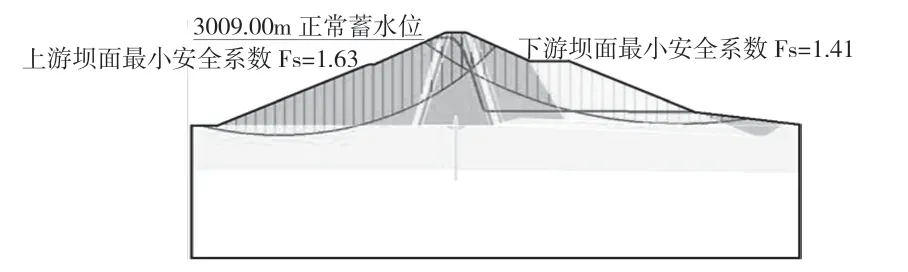
图7 地震作用下标准断面上下游坝坡滑动面

表3 坝坡抗滑稳定安全系数表

结果显示,标准断面在校核水位下的上游坝坡稳定安全系数为2.11,大于规范允许值1.2,且安全系数的富余量较大,说明上游坝坡在校核水位下处于稳定状态；下游坝坡稳定安全系数为1.72,虽然安全系数略低于同工况的上游坝坡,但仍大于规范允许值1.2,说明下游坝坡校核水位下处于稳定状态。

正常水位下的上游坝坡稳定安全系数为2.08,大于规范允许值1.3,且安全系数的富余量较大,说明上游坝坡在校核水位下处于稳定状态；下游坝坡稳定安全系数为1.73,虽然安全系数略低于同工况的上游坝坡,但却大于规范允许值1.3,说明下游坝坡正常水位下处于稳定状态。

地震作用下的上游坝坡稳定安全系数为1.63,大于规范允许值1.15,安全系数的富余量较小,说明上游坝坡在校核水位下处于基本稳定状态；下游坝坡稳定安全系数为1.41,虽然安全系数略低于同工况的上游坝坡,但却大于规范允许值1.15,说明下游坝坡在地震工况下处于稳定状态。同时地震作用下各个断面上下游坝坡最小安全系数均降低,说明该工况下上下游坝坡稳定性都有所下降,安全系数富余量减少,但仍在允许范围内。

6 结论

以甘肃省引洮（博）济合调蓄水库为例,采用变分有限元法对调蓄水库校核水位、正常蓄水位及地震作用下的渗流稳定及坝坡稳定性方面进行了分析研究,得出结论如下：

（1）由正常水位和校核水位两种工况下调蓄水库防渗体浸润线明显降低,坝体浸润线分布符合一般壤土心墙堆石坝规律,断面下游浸润线基本水平,具有较好的排渗效果。

（2）通过计算调蓄水库稳定性可知,三种工况下上下游坝坡稳定性安全系数都在允许范围内,校核水位安全系数富余量最大,地震作用安全系数富余量较小,上下游坝坡稳定性受地震作用有所下降。