带管路舱筏隔振系统动力学建模与管路设计方法

雷智洋，陈志刚，闫肖杰

（1.中国舰船研究设计中心，武汉 430064； 2.船舶振动噪声重点实验室，武汉 430064）

潜艇主辅机设备的机械噪声是低速巡航工况下的主要噪声源。采用舱筏减振技术可有效实现设备的振动传递隔离、降低辐射噪声水平[1-2]。

针对舱筏隔振系统的动力学建模，已发展了多刚体法、数值仿真方法和子结构综合方法，如四端参数法、传递矩阵法、阻抗综合法、模态综合法以及频响函数综合法。王真等[3]利用四端参数模型和阻抗综合法建立了柔性浮筏隔振系统动力学模型，开展隔振性能分析。门丽洁等[4]采用子结构导纳综合法建立了包含弹性基础的多激励源多自由度浮筏隔振系统动力学模型。张峰等[5]利用传递矩阵法研究了复杂隔振系统的多输入多输出振动传递特性。吴广明[6]利用模态综合法建立三维弹性耦合隔振系统动力学模型。黄修长等[7]利用频响函数综合方法建立舱筏隔振系统的多输入多输出模型。

舱筏隔振系统中包含管路、轴系等附连设备，形成振动传递的第二传递通道。采用舱筏隔振技术虽然可以有效控制通过减振器传递的振动，但管路等第二传递通道的设计不当会恶化系统的隔振效果，对舰船声隐身特性有很大的危害。但目前考虑附连设备的舱筏隔振系统振动传递建模较少。文献[8-10]关于第二传递通道对隔振性能的影响开展研究，但在指导设计方面仍显不足。徐时吟[11]通过三次综合过程，建立了考虑管路、轴系等附连设备的舱筏系统频响函数建模方法。

本文参考文献[11]的建模思路，基于频响函数综合方法和三次综合过程，建立带管路的一般的舱筏隔振系统动力学模型，开展动力学建模的验证以及三种管路连接方式下舱筏隔振系统的隔振效果对比分析，并给出管路的设计准则。

1 带附连管路舱筏隔振系统力学建模

带附连管路舱筏隔振系统子结构示意图如图1所示，子结构A为浮筏、子结构B为艇体-基座、子结构D为设备，子结构P为管路，各子结构间通过隔振器连接。

图1 带附连管路舱筏隔振系统子结构示意图

首先通过理论或实验获得A、B、D 和P 的频响函数矩阵，隔振器的阻抗矩阵。带附连管路舱筏隔振系统动力学建模步骤分为3 步：（1）利用第1 次频响函数综合得到AB频响矩阵：

（2）将子结构B的内点作为AB的连接点，其余节点为内点，进行综合体AB和子结构D第二次频响综合，得到第二次综合后的频响矩阵：

（3）将管路连接点作为ABD的连接点，其余节点为内点，子结构P的点均为连接点，进行综合体ABD和子结构P第三次综合，得到系统频响函数矩阵为[11]：

式中：上标Q代表管路子结构。

激励施加在设备D 的质心，利用式(3)可求得舱筏下部连接点、基座连接点、艇体上的管路连接点以及管路上连接点的响应为：

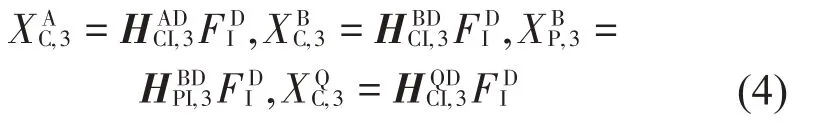
利用减振器上下两端的响应及其阻抗矩阵得到减振器传递力。由筏架下层减振器传入基座的力、经由管路传入艇体的力为：

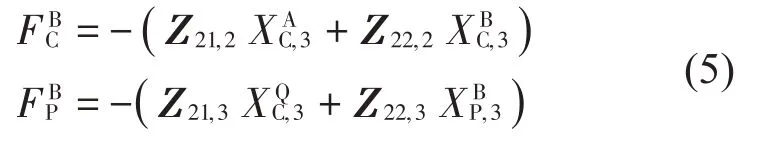
经减振器及管路传入基座艇体的功率流分别为：

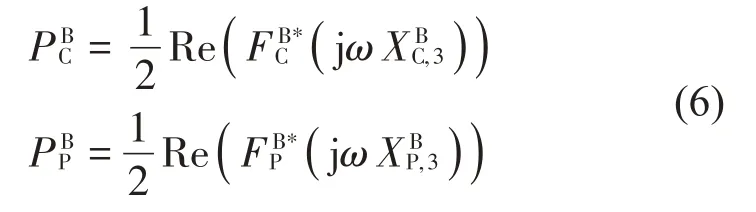
由传递到基座和艇体的传递力，以及减振器、管路与基座连接点、艇体连接点到艇体表面节点法向的频响函数矩阵，计算艇体表面节点法向振动响应Xf，由边界元法求得艇体表面法向声压Pf，艇体表面法向均方振速和辐射声功率为：

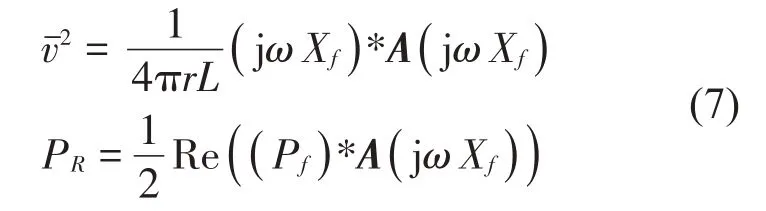
式中：r为艇体半径；L为艇体长度；A为面积矩阵。

2 数值仿真及分析

2.1 数值验证

验证模型如图2所示。计算中所采用的舱筏隔振系统模型包括设备、筏体和带基座的单层加筋艇体、管路，各子结构之间分别通过减振器弹性连接或刚性连接。筏体子结构A 为板架式筏架结构，采用矩形截面型钢焊接而成，总体尺寸为1.2 m×0.86 m×0.12 m，质量为76 kg，型钢的截面尺寸为0.12 m×0.06 m，壁厚为0.004 m，在ANSYS 中采用Shell181单元进行模拟。艇体-基座子结构B 为两端开口的圆柱形壳体，其长度为1.4 m，半径为0.75 m，壁厚为0.006 m。在艇体上布置4 个分立式小基座，各自之间的距离为0.5 m；每个小基座由两块垂直的面板和一块三角形肘板构成，面板采用边长0.3 m 的方形板，板厚为0.015 m，肘板的尺寸为0.225 m×0.2 m×0.015 m；在壳体上交错布置纵肋和环肋，截面均为矩形，截面尺寸为0.06 m×0.02 m，在ANSYS中采用Shell181 单元进行模拟。设备子结构D 为三个质量分别为65 kg、50 kg和65 kg的质量块，采用Solid185实体单元获得频响函数。管路子结构P 截面为圆环，外径为0.06 m，内径为0.047 5 m，长度0.6 m，在ANSYS 中采用梁单元Beam188 梁单元模拟。上述子结构均采用钢制作，弹性模量为2.1×1011N/m2，密度为7 850 kg/m3，泊松比为0.3。管路子结构连接在中间设备2和壳体中间截面之间。在管路的中间位置布置管路减振器与下方筏架进行连接。弹性连接时在管路与艇体连接位置采用挠性接管。隔振器及挠性接管采用Combine14单元进行模拟。隔振器布置在设备下部平面4个角点位置。综合时采用六向刚度参数，上层减振器（每个设备下各4个）、下层减振器（四个）、挠性接管、管路减振器基准刚度参数如表1所示。

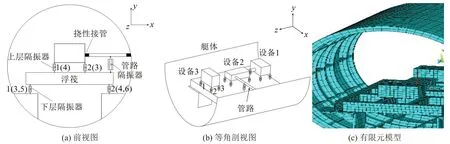
图2 验证模型(每设备下减振器按1，2，3，4逆时针编号)

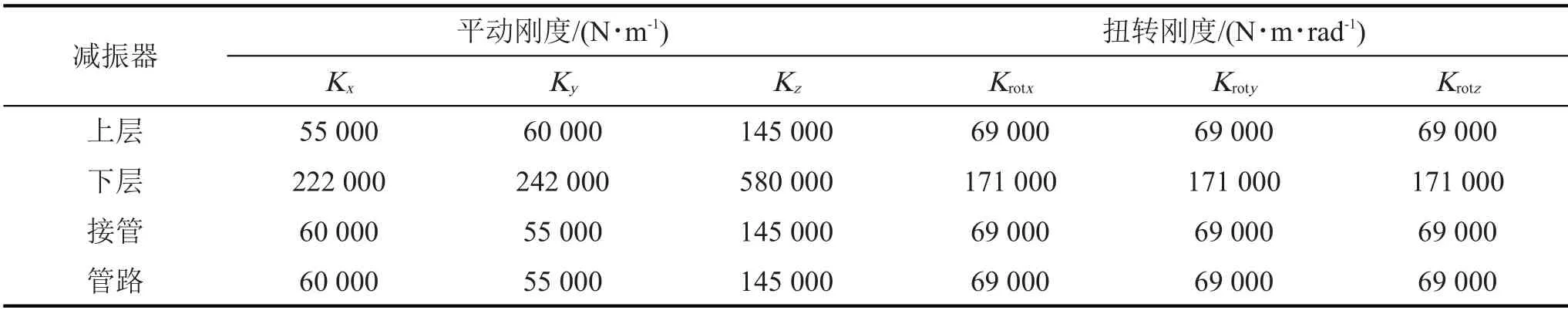
表1 上层减振器、下层减振器、挠性接管、管路减振器的基准刚度参数

下面通过上述算例，对频响函数综合方法及数值仿真结果进行比较。考虑舱筏隔振系统在单源单向激励下的工况，在设备2的质心位置（系统的对称中心）施加垂向单位力作为激励，图3为综合过程中采用六向自由度时的计算结果。可见，频响综合方法的结果具有足够的计算精度，通过两种方法得到的系统各层面的响应曲线基本重合，频响综合方法能够对舱筏隔振系统的振动传递特性做出准确的预报。

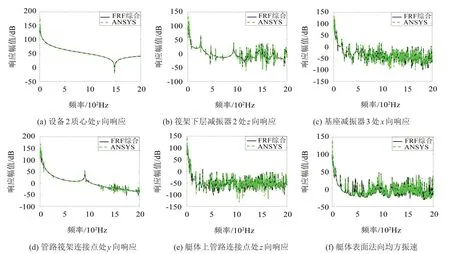
图3 有限元结果和频响函数综合结果比较（加速度响应的参考值为1×10-6 m/s2）

2.2 不同管路连接方式对比分析

针对图2中设备2的管路，提出以下三种管路连接方式，如图4所示。其中舱筏模型1中管路与设备2通过挠性接管连接，与艇体为刚性连接；舱筏模型2中设备2的管路分为两段，其中一段与设备2通过挠性接管连接，与浮筏为刚性连接，另外一段管路与浮筏为弹性连接，与艇体为刚性连接；舱筏模型3在舱筏模型2的基础上进行对称布置。在程序与仿真模型中，以1×10-6N/m 的六向刚度弹簧来模拟刚性连接。

图4 带管路的舱筏模型

在表1所示的参数下，比较舱筏模型1、2和3的响应，结果如图5 所示，给出了通过设备2 输入筏架的y 向力幅值，通过浮筏基座输入艇体的y 向力幅值，通过管路传递至艇体的功率流，通过下层减振器传递至艇体的功率流，通过上层减振器的功率流，设备2 质心y向响应，艇体表面法向均方振速，艇体辐射声功率。从图中可以看出：

图5 三种带管路舱筏模型振动声辐射结果比较

（1）舱筏模型1、2 和3 的艇体辐射声功率结果表明，模型2和模型3的辐射声功率在各个频段内均优于模型1，其中模型3 比模型2 在75 Hz～160 Hz频段内得到更大的下降。

（2）从设备2质心处的响应结果可知，舱筏模型1、2和3的隔振系统固有频率相同，三者的稳定性等基本性能相似。

（3）通过上层减振器的功率流以模型3 的结果较大，这是由于模型3的传递途径较多。

（4）通过浮筏基座输入艇体的y向力幅值，模型1、2和3的量级基本相当，部分频率点上模型1的峰值较大，这是由于模型1、2和3的连接方式不同导致系统模态不同；模型3 相对于模型2，在对应的峰值处响应略有减小，这是由于模型3相对于模型2来说为对称布置，其传递至浮筏的力更加均匀，这也可以从通过设备2输入筏架的y向力幅值得出结论。

（5）对通过管路传递至艇体的功率流和通过下层减振器传递至艇体的功率流进行比较，可知，虽然管路仅有1 或2 条传递通道，而基座有4 条传递通道，对于模型2 和3，这两条传递途径传递的功率流（能量）在各个频段基本处于同一量级；对于模型1，通过管路传递至艇体的功率流还大于通过下层减振器传递至艇体的功率流。模型1通过管路艇体弹簧输入艇体的功率流比模型2和3的大，这是由于模型1的管路直接连接设备和艇体，而模型2的管路首先连接在浮筏上，然后再通过减振器由中间浮筏和艇体连接，由于上层减振器的作用，传递至中间浮筏的振动得到衰减，同时由于中间浮筏是一大质量块，也能够有效阻挡振动传递，因此能有效降低通过管路传递至艇体的功率流。这也表明管路的设计对于降低振动传递和艇体声辐射具有重要价值。

从以上分析可知，采用模型2 的方案可以有效降低振动传递和声辐射，如果进一步采用模型3 所示的对称布置方案，对于进一步降低振动传递和声辐射有利。

3 结语

针对考虑管路的舱筏隔振系统，基于改进的频响函数综合子结构建模方法对其进行动力学建模，通过仿真计算验证方法的精度。利用该方法对3种带管路舱筏模型进行计算分析，得到以下结论：

（1）通过管路传递至艇体的功率流和通过下层减振器传递至艇体的功率流相比，可能更大或处于同一量级，因此管路的设计对于降低艇体振动声辐射具有重要的作用；

（2）为了降低设备振动导致的经由管路传递至艇体的力，应尽量避免管路直接将设备与艇体连接，并且可以适当地增加管路与中间筏体之间的连接，借助中间筏体的二次隔振作用，把管路传递至艇体的能量降至最低；

（3）可以通过对称布置管路，来减小由于不对称性造成的设备与浮筏之间的传递力放大。