New Hybrid EWMA Charts for Efficient Process Dispersion Monitoring with Application in Automobile Industry

Xuechen Liu,Majid Khan,Zahid Rasheed,Syed Masroor Anwarand Muhammad Arslan

1Faculty of Economics,Taiyuan Normal University,Taiyuan,030619,China

2Department of Mathematics and Statistics,Riphah International University,Islamabad,44000,Pakistan

3Department of Mathematics,Women University of Azad Jammu and Kashmir,Bagh,12500,Pakistan

4Department of Statistics,University of Azad Jammu and Kashmir,Muzaffarabad,13100,Pakistan

5School of Statistics,Shanxi University of Finance and Economics,Taiyuan,030619,China

ABSTRACT The EWMA charts are the well-known memory-type charts used for monitoring the small-to-intermediate shifts in the process parameters(location and/or dispersion).The hybrid EWMA(HEWMA)charts are enhanced version of the EWMA charts,which effectively monitor the process parameters.This paper aims to develop two new uppersided HEWMA charts for monitoring shifts in process variance,i.e.,HEWMA1 and HEWMA2 charts.The design structures of the proposed HEWMA1 and HEWMA2 charts are based on the concept of integrating the features of two EWMA charts.The HEWMA1 and HEWMA2 charts plotting statistics are developed using one EWMA statistic as input for the other EWMA statistic.A Monte Carlo simulations method is used as a computational technique to determine the numerical results for the performance characteristics,such as average run length(ARL),median run length,and standard deviation run length(SDRL)for assessing the performance of the proposed HEWMA1 and HEWMA2 charts.In addition,to evaluate the overall performance of the proposed HEWMA1 and HEWMA2 charts,other numerical measures consisting of the extra quadratic loss(EQL),relative average run length(RARL),and performance comparison index(PCI)are also computed.The proposed HEWMA1 and HEWMA2 charts are compared to some existing charts,such as CH,CEWMA,HEWMA,AEWMA HHW1,HHW2,AIB-EWMA-I,and AIB-EWMA-II charts,on the basis aforementioned numerical measures.The comparison reveals that the proposed HEWMA1 and HEWMA2 charts achieve better detection ability against the existing charts.In the end,a real-life data application is also provided to enhance the implementation of the proposed HEWMA1 and HEWMA2 charts practically.

KEYWORDS Average run length;extra quadratic loss;memory-type charts;Monte Carlo simulations;smoothing parameter

1 Introduction

Control charts are the essential tools of the statistical process monitoring(SPM)toolkit,used to detect the shifts in manufacturing and production processes parameter(s).The control charts are generally classified into memory-type and memoryless-type charts[1].The memoryless-type charts are used only for current information of the process,while the memory-type charts are based on both current and previous information of the process.The basic memoryless-type charts are the Shewhart charts,like the Shewhart,R,andS2charts,etc.[2].The Shewhart charts are simple and easy to apply;however,they are only efficient for the cases where large shifts occur in the process parameter(s).On the contrary,the memory-type charts,such as the exponentially weighted moving average(EWMA)and cumulative sum(CUSUM)charts are sensitive in monitoring smallto-intermediate shifts in the process parameter(s).

Roberts[3]was the first to introduce the classical EWMA chart for monitoring the mean level of the process.Later,Hunter et al.[4–7]further investigated the various EWMA-type charts in order to facilitate the application of the classical EWMA chart in mean process monitoring.Recent studies have shown that EWMA-type charts are the most useful tools for researchers.For example,Haq[8],Abbas et al.[9],Ali et al.[10],Tang et al.[11],Haq[12],Rasheed et al.[13],Rasheed et al.[14],etc.,are the few recent references in this regard.

In general,most manufacturing and production processes have a shift in the mean level;however,the process variance(or standard deviation)may be shifted from the target in many practical situations.Domangue et al.[15]suggested that monitoring an increase in process variance is more important for the processes.Although the EWMA-types charts are primarily used in mean process monitoring;however,few works address the variance monitoring via these charts.For example,Crowder et al.[16]used the logarithmic transformation to the sample varianceS2in order to develop the EWMA chart(also known as the CH chart)for monitoring the process standard deviation.Similarly,Shu et al.[17]suggested the EWMA chart,denoted as the NEWMA chart,efficiently monitors process variance compared to the CH chart.Correspondingly,Huwang et al.[18]developed the EWMA-type charts for detecting shifts in the process variance and demonstrated that their control charts outperform the CH and NEWMA charts.Equally,Castagliola[19]used the three parameters logarithmic transformation ofS2and proposed the bilateral EWMA chart to monitor the process variance shifts.Besides,Chang et al.[20]designed the optimal EWMA chart in order to monitor the process variance shifts.In addition,Razmy[21]offered the EWMA chart the monitors the standardized process variance.Furthermore,Haq[22]proposed two auxiliary information-based charts,symbolized by AIBEWMA1 and AIBEWMA2 charts,that monitor the process variance efficiently.Also,Ali et al.[23]suggested the generally weighted moving average(GWMA)and hybrid EWMA(HEWMA)chart to monitor process variance changes.Both GWMA and HEWMA perform better than classical memory charts.Other studies based on the EWMA-type charts for tracking the process variance are provided by Saghir et al.[24],Zaman et al.[25],Riaz et al.[26]and Chatterjee et al.[27],etc.

The use of hybrid charts enhances the efficiency of traditional charts.For example,Haq[8]and Haq[28]proposed the HEWMA chart to monitor the mean level of the process.Later on,numerous authors used the HEWMA charts in different process monitoring schemes.The HEWMA charts are more efficient than the classical EWMA and CUSUM charts in terms of small to moderate shifts monitoring.For example,Aslam et al.[29]introduced the HEWMA chart to monitor the mean level of the process under repetitive sampling.Similarly,Aslam et al.[30]monitored the COM-Poisson process by designing the HEWMA chart.Equally,Aslam et al.[31]developed the mixed chart,named the HEWMA-CUSUM chart,for the Weibull process monitoring.Correspondingly,Noor-ul-Amin et al.[32]recommended the HEWMA chart for Phase-II mean monitoring,based on the auxiliary information.Besides,Aslam et al.[33]suggested the HEWMA-pchart to monitor the variance of the non-normal process.Also,Noor et al.[34]constructed the Bayesian HEWMA chart,using two loss functions,to monitor the mean level of the normal process.The other studies about the HEWMA chart are offered by Asif et al.[35],Noor-Ul-Amin et al.[36],etc.

The majority of manufacturing and service processes are affected by the gradual increase in process variance.The increase in the process variance indicates a deterioration in the process performance.This study’s first and most important goal is to propose efficient charts with effective shifts detection ability in monitoring an increase in the process variances.So,motivated by Crowder et al.[16],Castagliola[19],and Haq[8],this study proposes two new HEWMA charts to monitor the increasing shifts in the process variance.The proposed charts are known as HEWMA1 and HEWMA2 charts.The design structure of the HEWMA1 chart uses the CH statistic as the input for the HEWMA1 statistic.In the same lines,the CEWMA statistic is considered an input to the HEWMA2 statistic to formulate the HEWMA2 chart.The Monte Carlo simulations are employed to compute the numerical results associated with average run length(ARL),standard deviation run length(SDRL),extra quadratic loss(EQL),relative average run length(RARL),and performance comparison index(PCI)for the proposed HEWMA1 and HEWMA2 charts.Based on these measures,the proposed HEWMA1 and HEWMA2 charts are compared to the existing CH,CEWMA,HEWMA,AEWMA,HHW1,HHW2,AIBEWMA1,and AIBEWMA2 charts.The comparison shows that the proposed HEWMA1 and HEWMA2 charts have better detection ability to detect the shift in the process variance.Finally,two applications of the proposed HEWMA1 and HEWMA2 charts are provided,one with simulated data and the other with real-life data,to aid in the comparison of the proposed charts.

The remainder of the article is set out in the following way:Section 2 presents the existing methods.Likewise,Section 3 lays out the methodologies and formulation of the proposed HEWMA1 and HEWMA2 charts.In addition,the performance evaluation measures and simulation study are included in Section 4.Furthermore,Section 5 consists of the comparison and performance analysis of the proposed HEWMA1 and HEWMA2 charts against some existing charts.Section 6 offers a real-life data application to enhance the performance of the proposed HEWMA1 and HEWMA2 charts.The last section addresses the concluding remarks.

2 Existing Schemes

This section defines the process variable in Subsection 2.1.Similarly,Subsection 2.2 explains the details about the transformations to the sample variance.In addition,Subsections 2.3 to 2.6 provide the design and formulation of the CH,CEWMA,HHW2,and HEWMA charts for monitoring process variance,respectively.

2.1 Process Variable

2.2 Transformation

In order to implement the EWMA-type charts,the assumption of normality is required for the plotting statistic of the charts.However,because the sample variancehas a chi-square distribution,so it is not an acceptable statistic for the design structure of the EWMA-type charts.In order to cope with this issue,a few transformations are available in the literature,given as follows.

2.2.1 Transformation-I

LetWtdenote a log transformation of,defined as

2.2.2 Transformation-II

Castagliola[19]recommended the three-parameter logarithmic transformation ofinto a new variable,given as

2.2.3 Transformation-III

In order to detect the shifts in the process variance,Quesenberry[38]suggested another transformation defined as

2.3 CH Chart

Crowder et al.[16]introduced the CH chart,which monitored the process variance shifts.Let{Qt}fort≥1 be the sequence of IID random variable,defined on the sequence {Wt},whereWtis defined by Eq.(1),then using the recurrence relationship,the CH plotting statisticQtcan be given as

whereλ1is known as the smoothing parameter.The CH statistic mean and variance are,respectively,given as

2.4 CEWMA Chart

Castagliola[19]proposed the EWMA chart(also known asS2-EWMA chart)to monitor the shifts in the process variance.Hereafter theS2-EWMA chart is labeled as the CEWMA chart.The CEWMA chart used the three parameters logarithmic transformation toS2to obtain the approximate normality for the plotting statistic.Let {Zt} be the CEWMA sequence,based on another sequence {Tt}fort≥1,whereTtis defined by Eq.(2),then the charting statistic of the CEWMA chart is given by

The initial value ofZtis denoted byZ0and can be is defined as

2.5 HHW2 Chart

2.6 HEWMA Chart

3 Proposed Methods

Haq[8]suggested the HEWMA chart to monitor the process mean.Similarly,Ali et al.[23]presented the HEWMA chart’s design structure for tracking the process variance.Following Haq[8],the HEWMA1 and HEWMA2 charts can be developed using Transformations I and II,respectively.These charts detect increasing shifts in process variance.The methodologies and construction of the HEWMA1 and HEWMA2 charts are,respectively,presented in Subsections 3.1 and 3.2.

3.1 HEWMA1 Chart

The design structure for the HEWMA1 chart can be constructed using the CH statistic as input for the HEWMA1 statistic.Let defined the sequence of IID random variable,say {Ut}fort≥1,based on the CH sequence {Qt} then the HEWMA1 statisticUtcan be defined by the relation given as

whereQtis the CH statistic defined by Eq.(4).The starting value ofUtis equal to 0,i.e.,U0=0.The mean ofUtisE(Ut)=0 and its variance,for the case of very larget,is defined as

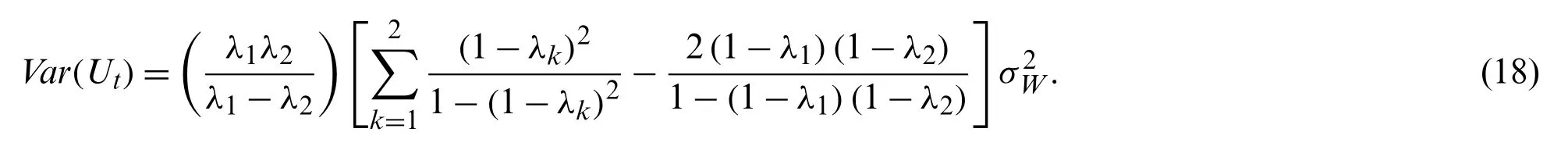
In order to monitor the increasing shift in the process,the HEWMA1 statistic is defined as

3.2 HEWMA2 Chart

In order to formulate the design of the HEWMA2 chart,the charting statistic of the CEWMA chart can be used as an input for the HEWMA2 statistic.Let {Vt} fort≥1 be the HEWMA2 sequence,then the HEWMA2 chart statistic isVt,and it can be defined by

whereZtis the HHW2 plotting statistic defined by Eq.(7).The starting values ofVtis equal toZ0defined by Eq.(8).The expected value for the statisticVtisE(Vt)=μTand its variance is given as

The HEWMA2 control limitsUCLt(HEWMA2)andLCLt(HEWMA2)are given as

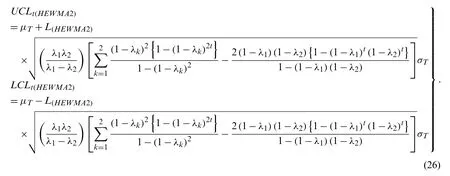
The control limits defined in Eq.(26)are known as the two-sided time-dependent control limits;however,in the case of largetvalues,the two-sided fixed HEWMA2 control limits are defined as

In this case,The HEWMA2 chart triggers OOC signals wheneverVt≥UCL(HEWMA2)orVt≤LCL(HEWMA2).The control limits specified in Eq.(27)are the two-sided control limits;however,the HEWMA2 upper control limit is defined as

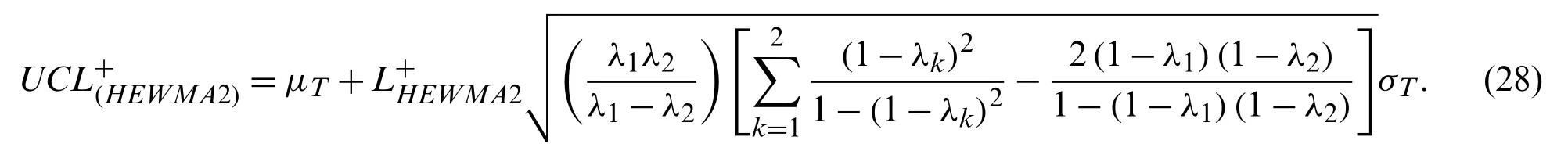
4 Performance Analysis and Simulation Study

This section defines the performance evaluation measures,such as average run length in Subsection 4.1 and overall performance measures in Subsection 4.2.Similarly,the simulation study for the proposed HEWMA1 and HEWMA2 charts is designed in Subsection 4.3.Likewise,Subsection 4.4 provides the choices design parameters for the proposed HEWMA1 and HEWMA2 charts.

4.1 Average Run Length

The most popular and commonly used performance evaluation measures are the ARL and SDRL measures.The ARL can be defined as the average number of sample points until a chart indicates the OOC signal[2].The ARL is further categorized as IC ARL(ARL0),and OOC ARL(ARL1).When a process is working in an IC state,the ARL0should be as large enough to prevent the frequent false alarms,while the ARL1should be smaller so that the shift is detected quickly[39].A chart with smaller ARL1is preferred over the competing charts at a prespecified ARL0[40].

4.2 Overall Performance Evaluation Measures

The ARL and SDRL measures evaluate the performance of the charts on a single specified shift.However,sometimes the researcher may want to investigate the charts performances for the entire range of shifts,i.e.,δmin ＜δ ＜δmax.For this purpose,the other performance measures,such as extra quadratic loss(EQL),relative average run length(RARL),and performance comparison index(PCI),are used.The details on the EQL,RARL,and PCI measures are provided in the following subsections.

4.2.1 Extra Quadratic Loss

The EQL can be considered as a weighted average of ARL defined over the range of shiftsδmintoδmax,usingδ2as a weight.Symbolically,the EQL can be defined as

where ARL(δ)is the ARL at specific shiftδandδminandδmaxare the minimum and maximum shift values,respectively.A chart with a low EQL value is considered to have a better overall detection ability[41].

4.2.2 Relative Average Run Length

Like the EQL measure,the RARL also evaluates the overall performance of the charts.The RARL mathematically can be defined as

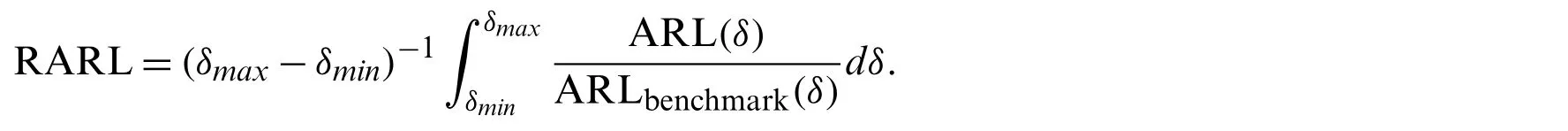
where ARLbenchmark(δ)is the ARL value for benchmark chart at shiftδ.A chart with a smaller ARL at specificδis known as a benchmark chart.The RARL value for the benchmark chart is always equal to 1.The benchmark chart is considered superior to the competing chart if RARL＞1[42].

4.2.3 Performance Comparison Index

The PCI also assesses the overall performance of the best chart.Ou et al.[43]defined the PCI as a ratio of EQL of the best chart to the EQL of the benchmark chart.Mathematically,it can be given by the expression given as

The PCI value for the benchmark chart is equal to be 1,and for the rest of the charts,PCI＞1[44].

4.3 Monte Carlo Simulations

The random sample of sizen,i.e.,X1t,X2t,...,Xit,...,Xntfort ＞1,is generated from a normal distribution under different parameter settings.Domangue et al.[15]suggested that monitoring a gradual rise(process deterioration)in the process variance is more important;therefore,an upward shift is considered in the process variance.The shift is reflected in the process standard deviation,i.e.,σ=δσ0,whereδ=1.0,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9 and 2.0.The Monte Carlo simulation approach is utilized as a computational methodology for the numerical results by designing an algorithm in the statistical package R.At each shift sizeδ,the simulations are performed with 20,000 replicates.The simulation algorithm for the HEWMA1 and HEWMA2 charts include the following steps:

4.4 Choices of Design Parameters

The design parameters for the proposed HEWMA1 and HEWMA2 charts are the smoothing constantsλ1,λ2and the chart width coefficientLproposed,which have a certain effect on the chart performance.Therefore,the different settings of the design parameters are used in computing ARL,MDRL and SDRL measures.The various combination of smoothing parameters are chosen as(λ1=0.05,λ2=0.050001,0.1,0.20),(λ1=0.1,λ2=0.05,0.100001,0.20),(λ1=0.2,λ2=0.05,0.1,0.200001),(λ1=0.3,λ2=0.05,0.1,0.2)to determine the values ofandso that ARL0=200.The numerical results regarding the proposed HEWMA1 and HEWMA2 charts are displayed in Tables 1–4.

5 Comparative Study

This section addresses the detailed comparative study of the proposed charts to the existing charts.The ARL values in Tables 1–4 reveal that the HEWMA2 chart outperforms the HEWMA1 chart;therefore,the HEWMA2 chart is recommended to compare with the existing charts for better detection performance.Thus the HEWMA2 charts is compared against the existing CH[16],CEWMA[19],HEWMA[23],AEWMA[45],AIBEWMA1,and AIBEWMA2[22]charts.Table 5 presents the ARL values for comparison,while Table 6 contains the overall performance values.The following Subsections offer further details about the comparisons.

5.1 Proposed vs.CH Chart

The proposed HEWMA2 chart achieves better performance against the CH chart.For example,at ARL0=200,withλ1=0.1,0.2,λ2=0.05 andδ=1.1,the proposed HEWMA2 charts provide the ARL1values 25.40 and 26.91,respectively,whereas the CH chart produces the ARL1=44.26,46.63,respectively(see Table 5 &Fig.1).Similarly,the proposed HEWMA2 chart indicates improved overall performance against the CH chart.As forλ1=0.1 andλ2=0.05 the EQL,PCI,and RARL values of the proposed HEWMA2 charts are 19.5141,1.0000,and 1.0000,which are less than the EQL,PCI,and RARL values of the CH chart;27.7505,1.4221,and 1.8851(see Table 6).

5.2 Proposed vs.CEWMA Chart

The proposed HEWMA2 chart shows lower ARL1values when it is compared to the CEWMA chart.For instance,assuming ARL0=200,withλ1=0.1,0.2,λ2=0.05 andδ=1.1 the proposed HEWMA2 chart has ARL1values of 25.40 and 26.91,respectively,whereas the CEWMA chart owns the ARL1values of 31.80 and 37.80(see Table 5 &Fig.1).Similarly,in terms of overall performance(see Table 6),the proposed HEWMA2 charts attained smaller the EQL,PCI,and RARL values,i.e.,20.1797,1.0000,and 1.0000 against the CEWMA chart the EQL,PCI,and RARL values,i.e.,23.5747,1.1682,and 1.2818,respectively,whenλ1=0.2,andλ2=0.05.

5.3 Proposed vs.HEWMA Chart

The proposed HEWMA2 chart achieves superior performance over the HEWMA chart.For instance,at ARL0=200,λ1=0.1,λ2=0.05 andδ=1.2,1.3,1.4,1.5 the proposed HEWMA2 chart gives the ARL1values 9.94,5.73,3.87,2.87,whereas the HEWMA chart yields the ARL1=10.11,5.75,3.92,2.96(see Table 5 &Fig.2).Similarly,the proposed HEWMA2 chart indicates improved overall performance against the HEWMA chart.For example,the proposed charts deliver the EQL,PCI,and RARL values as 19.5141,1.0000,1.0000,respectively;however,the HEWMA chart provides the EQL,PCI,and RARL values as 20.6981,1.0607,and 1.1126,respectively(see Table 6).

5.4 Proposed vs.AEWMA Chart

Haq[45]developed the adaptive EWMA(AEWMA)chart for monitoring the process variance.The proposed HEWMA2 chart is compared to the AEWMA chart at ARL0=200,and the results indicate that the proposed HEWMA1 and HEWMA2 chart has better detection ability against the AEWMA chart for the small shift,i.e.,1＜δ≤1.2.For instance,with ARL0=200,λ1=0.1,λ2=0.05 andδ=1.1,1.2,the proposed HEWMA-2 charts deliver the ARL1values as 25.40,9.94,while the AEWMA chart has the ARL1values equal to 26.04,10.35(see Table 5&Fig.2).Likewise,whenλ1=0.2 andλ2=0.05,the overall performance of the proposed HEWMA2 chart is superior to the AEWMA chart as the proposed chart has a smaller EQL=20.1797 than the AEWMA chart EQL=20.3854(see Table 6).

5.5 Proposed vs.AIBEWMA1 and AIBEWMA2 Charts

Haq[22]proposed the AIBEWMA1 and AIBEWMA2 charts for monitoring the process variance.The comparison of the HEWMA2 chart against the AIBEWMA1 and AIBEWMA2 charts demonstrates that the proposed HEWMA2 chart is more efficient than the AIBEWMA1 and AIBEWMA2 charts.For example,with chart properties,i.e.,ARL0=200,λ1=0.1,λ2=0.05,ρ=0.5 andδ=1.1 the ARL1values for the proposed HEWMA2 charts is observed as 25.40,while the ARL1values for the AIBEWMA1 and AIBEWMA2 charts are reported as 30.11 and 30.79(see Table 5 &Fig.3).Likewise,the proposed charts’EQL,PCI,and RARL values also show the edge in the overall detection ability of the HEWMA2 chart over the AIBEWMA1 and AIBEWMA2 charts.As the EQL,PCI,and RARL values for the proposed HEWMA2 charts are 19.5141,1.0000,and 1.0000,respectively,where EQL,PCI,and RARL values for the AIBEWMA1 and AIBEWMA2 charts are 20.8605,1.0690 and 1.1185,and 21.4587,1.0996 and 1.1919,respectively(see Table 6).

6 Important Points of the Study

A few important points related to the HEWMA1 and HEWMA2 charts can be listed as:

(i)The HEWMA statistics undoubtedly boost the efficiency of the proposed HEWMA1 and HEWMA2 charts.

(ii)The proposed HEWMA2 chart has better detection performance than the proposed HEWMA1 chart(see Tables 1–4).

(iii)At different parametric settings,the ARL1values for the proposed HEWMA1 and HEWMA2 charts are less than the ARL1values of the CH,CEWMA,HEWMA,AEWMA,AIBEWMA1,and AIBEWMA2 charts(see Section 5).

(iv)The overall performance reveals the dominance of HEWMA1 and HEWMA2 charts over the CH,CEWMA,HEWMA,AEWMA,AIBEWMA1,and AIBEWMA2 charts(see Section 5).

(v)The proposed HEWMA1 and HEWMA2 charts have better ARL1performance for smallerλ1andλ2(see Tables 1–4).

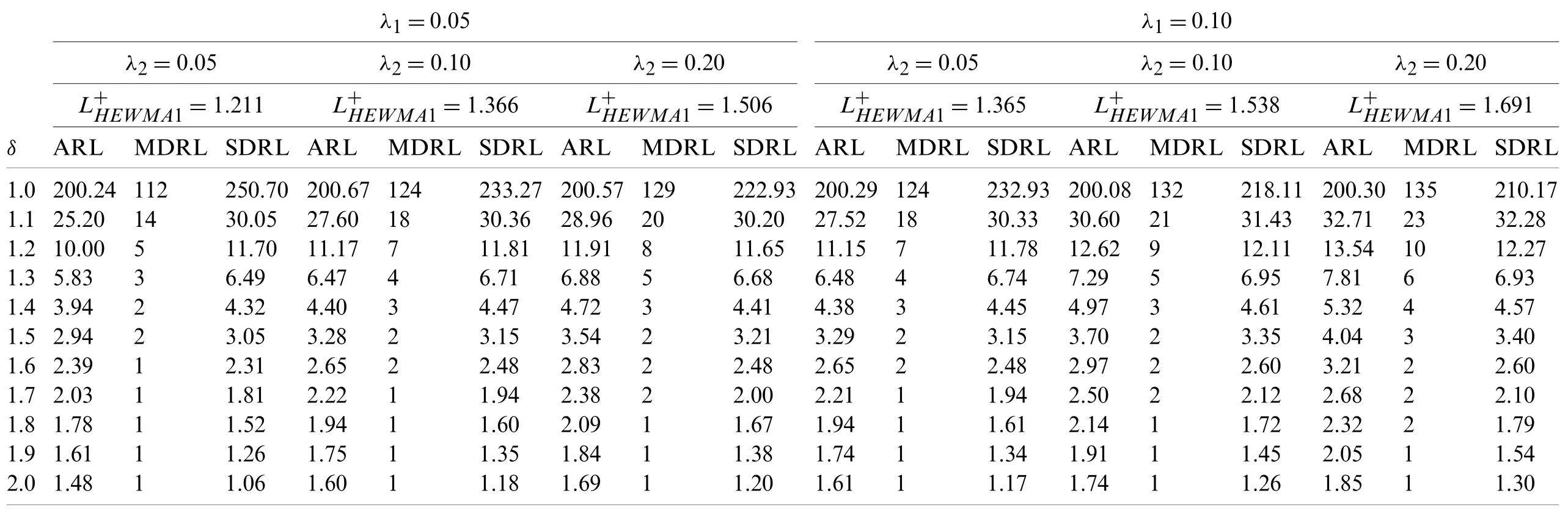
Table 1:Run-length properties of proposed HEWMA1 chart when λ1 is small and ARL0=200

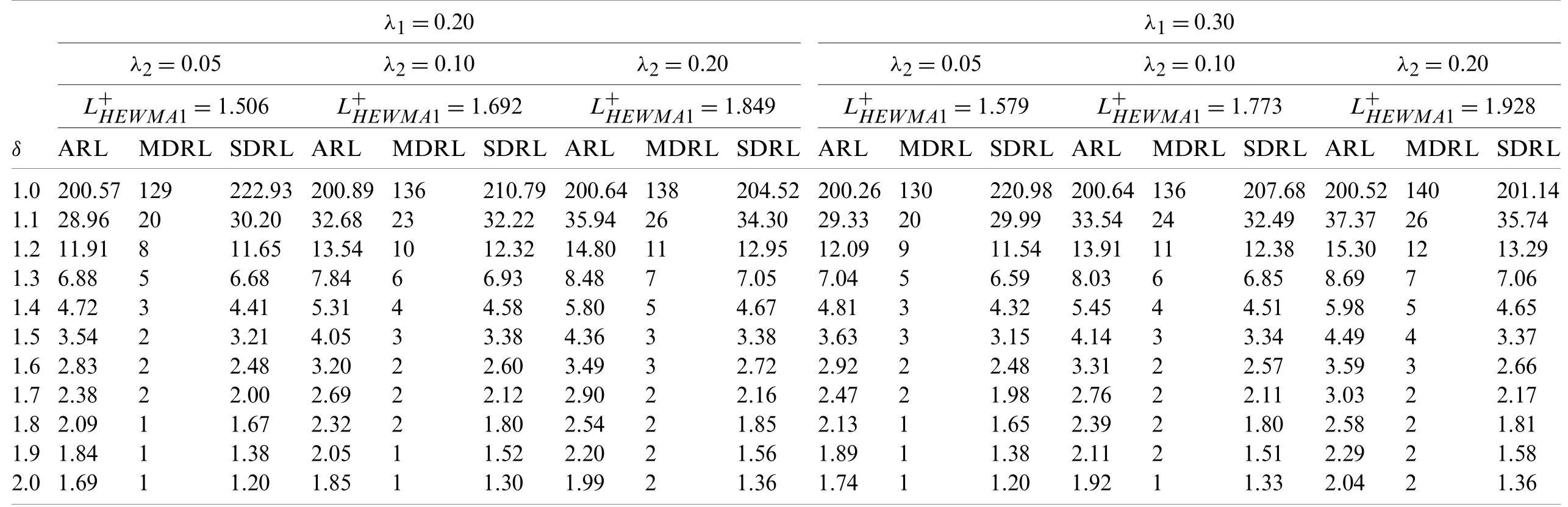
Table 2:Run-length properties of proposed HEWMA1 chart when λ1 is moderate and ARL0=200

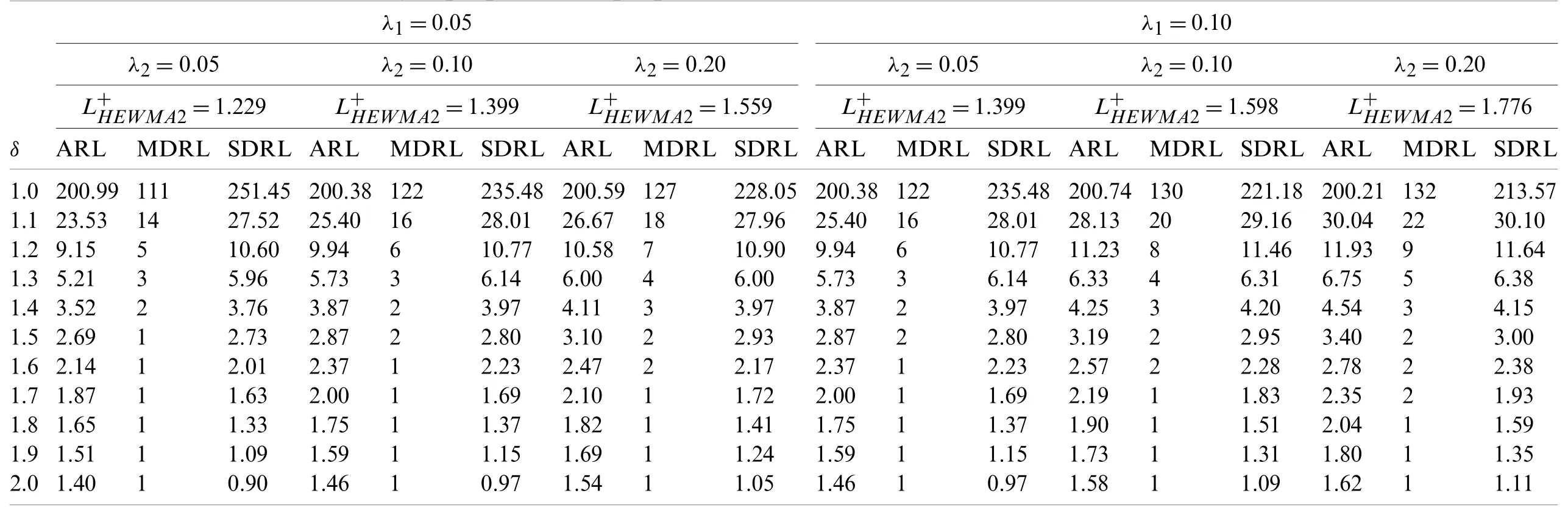
Table 3:Run-length properties of proposed HEWMA2 chart when λ1 is small and ARL0=200

Table 4:Run-length properties of proposed HEWMA2 chart when λ1 is moderate and ARL0=200

Table 5:ARL values for the proposed HEWMA1 and HEWMA2 vs.existing charts when λ2=0.05 at ARL0=200

Table 6:Overall performance measures for the proposed HEWMA1 and HEWMA2 vs.existing charts

(vi)The control limit coefficientLfor the suggested HEWMA1 and HEWMA2 charts increases asλ1andλ2increases.

7 Real-life Application of the Proposed Charts

This subsection explains the application of the proposed HEWMA1 and HEWMA2 charts to real-life data.For this purpose,the real-life data are considered,representing the inside diameter of the cylinder bores in an engine block.These real-life data are used by[46,47]in their studies.The data comprise 30 samples,each sizen=5 given in Table 7.In order to implement the proposed HEWMA1 and HEWMA2 control along with CH and CEWMA charts,following[23,48],an upward shift of sizeδ=1.25 is introduced artificially after sample number 16[49,50].At ARL0=200,the smoothing parameter valuesλ1=0.1,λ2=0.05 are used,which provides the width of the the HEWMA1,and HEWMA2,CH and CEWMA charts,respectively,given asUsing the aforementioned parameters,the charting statistics for the HEWMA1,and HEWMA2,CH and CEWMA charts and their corresponding upper control limits are computed.The charting statistics for HEWMA1,and HEWMA2,CH and CEWMA charts are given in Table 7,while their corresponding upper control limits are given as 0.1528,0.1314,0.2547,and 0.4876,respectively.Figs.4–7 display the charting statistics of the CH,CEWMA,HEWMA1,and HEWMA2 charts against sample number.The results show that the proposed HEWMA1 chart outperforms the CH chart as the proposed HEWMA1 chart trigger the first OOC point after sample number 25,while the CH chart detects OOC point after sample number 28.Overall,the proposed HEWMA1 chart declares 7 OOC points,while the CH chart detects 2 OOC signals.Similarly,the HEWMA2 chart gains better detection ability relative to the CEWMA chart,as as the proposed HEWMA2 chart identifies the first OOC signal at sample number 26,while the CH chart diagnoses OOC signal at sample number 29.This indicates that the proposed HEWMA1 is more efficient than the CH chart,and the HEWMA2 chart achieves better detection ability than the CHWMA chart.

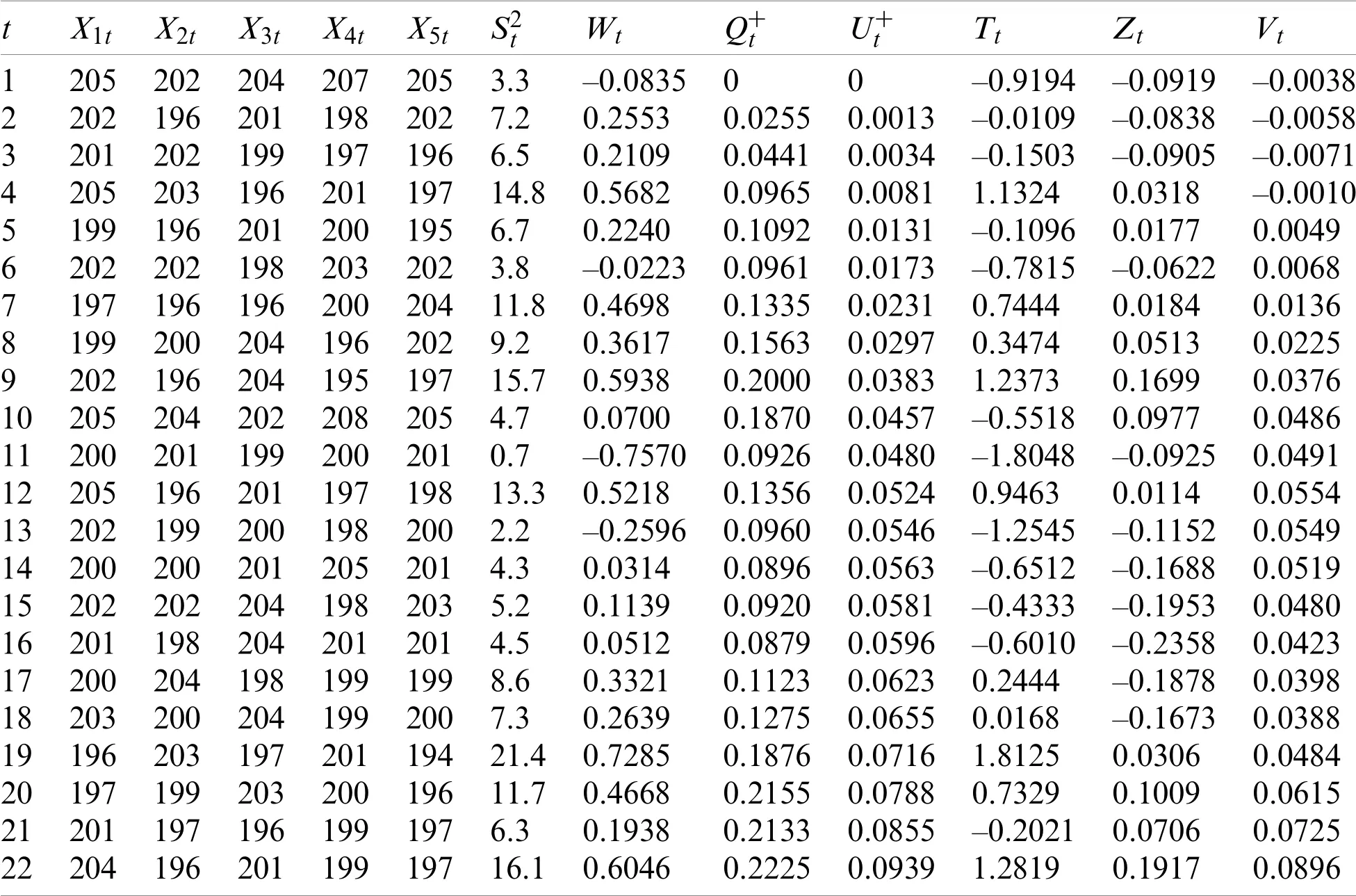
Table 7:Real-life data along with charting statistics for CH,CEWMA,HEWMA1,and HEWMA2 charts

Table 7(continued)tX1t X2t X3t X4t X5t S2tWtQ+tU+tTtZtVt 23 206 206 199 200 203 16.7 0.62110.2293 0.1037 1.35080.2076 0.1120 24 204 203 199 199 197 13.8 0.53620.2340 0.1142 1.00370.2372 0.1371 25 199 201 201 194 200 13.3 0.52120.2347 0.1252 0.94390.3339 0.1641 26 201 196 197 204 200 16.1 0.60460.2417 0.1370 1.28190.3787 0.1943 27 203 197 199 197 201 10.6 0.42430.2480 0.1486 0.57320.4541 0.2234 28 203 197 199 197 201 10.6 0.42430.2494 0.1598 0.57320.4990 0.2515 29 197 194 199 200 199 8.90.34760.2550 0.1704 0.29810.5059 0.2770 30 200 201 200 197 200 3.6–0.0465 0.2693 0.1783–0.8374 0.3716 0.2941 31 199 199 201 201 201 1.9–0.3291 0.2334 0.1826–1.3633 0.1981 0.3010 32 200 204 197 197 199 13.0 0.51080.2482 0.1879 0.90320.2686 0.3114

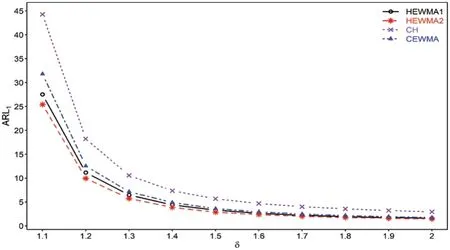
Figure 1:Comparison of proposed HEWMA1 and HEWMA2 charts with CH and CEWMA charts at(λ1,λ2)=0.1 and ARL0=200

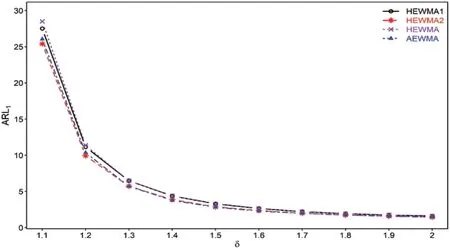
Figure 2:Comparison of proposed HEWMA1 and HEWMA2 charts with HEWMA and AEWMA charts at(λ1,λ2)=0.1 and ARL0=200

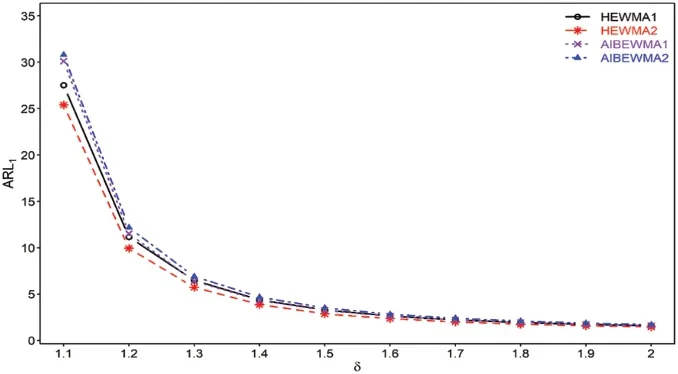
Figure 3:Comparison of proposed HEWMA1 and HEWMA2 charts with AIBEWMA1 and AIBEWMA2 charts at(λ1,λ2)=0.1 and ARL0=200

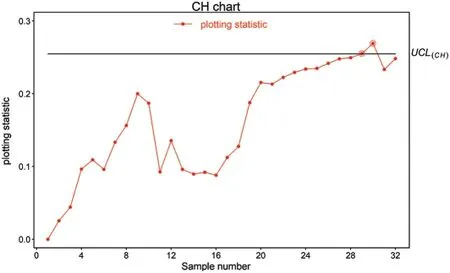
Figure 4:Real-life application of CH chart using(λ1,λ2)=(0.1,0.05) and ARL0=200

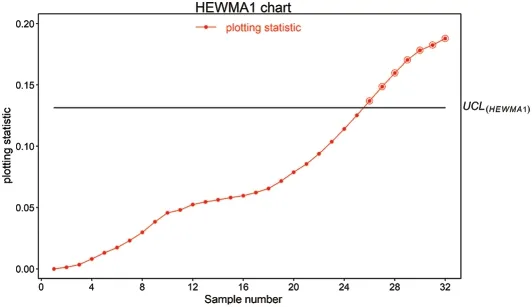
Figure 5:Real-life application of proposed HEWMA1 chart using(λ1,λ2)=(0.1,0.05) and ARL0=200

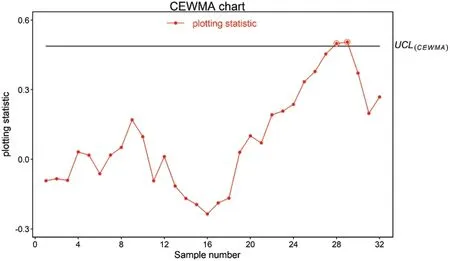
Figure 6:Real-life application of CEWMA chart using(λ1,λ2)=(0.1,0.05) and ARL0=200

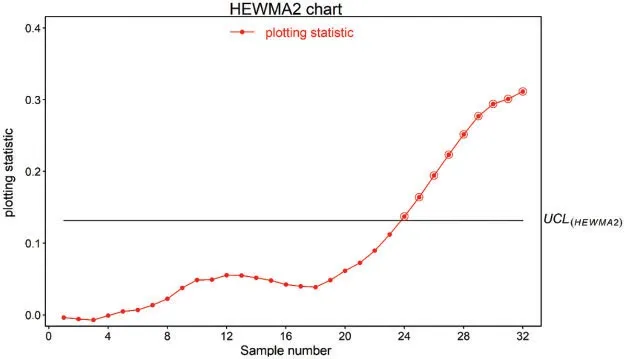
Figure 7:Real-life application of proposed HEWMA2 chart using(λ1,λ2)=(0.1,0.05) and ARL0=200

8 Concluding Remarks

This paper proposes two new hybrid EWMA charts to monitor the shifts in the process variance.The proposed charts are called HEWMA1 and HEWMA2 charts.The HEWMA1 chart is designed using the CH statistic as the input for the HEWMA1 statistic,while in the same lines,CEWMA statistic is used as the input for the HEWMA2 statistic to construct the proposed HEWMA2 chart.In order to evaluate the performance of the proposed HEWMA1 and HEWMA2 charts,the extensive Monte Carlo simulation approach is used to approximate the run length properties,including the average run length and standard deviation run length.Similarly,to assess the overall performances of the proposed HEWMA1 and HEWMA2 charts,the extra quadratic loss,relative average run length,and performance comparison index are computed.The proposed HEWMA1 and HEWMA2 charts are compared to existing CH,CEWMA,HEWMA,AEWMA,HHW1,HHW2,AIBEWMA1,and AIBEWMA2 charts,and the comparison indicates that the proposed HEWMA1 and HEWMA2 charts outperform the existing charts.In the end,real-life data are analyzed to enhance the efficiency of the proposed HEWMA1 and HEWMA2 charts.

Funding Statement:2019 Shanxi Province Soft Science Research Program Project “Research on Sustainable Development Capacity and Classification Construction of Shanxi Development Zone”(Project No.2019041005-2).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.