双层框架铁路对邻近建筑物的振动影响
陈以庭 冯读贝 杨吉忠 金旭炜
(中铁二院工程集团有限责任公司, 成都 610031)
为提高城市建成区既有单线走廊的运输效率,在有限空间内将单线扩建为地上、地下单线的双层布置形式成为一种可能,需确定双线框架结构铁路对邻近住宅建筑物的振动影响,但目前尚无案例和相关标准可参考。近年来,针对车致振动的影响开展了大量的研究,王祥秋[1]等对广州金沙隧道往广州南站方向270 km/h高速列车引起建筑物响应进行现场实测,得到列车产生振动频率集中在25~60 Hz范围内,铅垂向Z振级达到70.62 dB,建筑物二次振动具有明显高度放大效应;张凌[2]等对南昌西站候车厅车致振动进行现场实测,发现梁柱结构的约束作用对高于40 Hz的高频振动传播抑制明显;Connolly[3-4]等对欧洲7国17个高速铁路车站点进行现场测试,基于频谱分析获得近场传播频率集中在15~30 Hz范围内,27~31 Hz内有明显峰值。
关于既有铁路扩建为地上、地下单线双层铁路的车致振动影响研究,目前在国内、外相关领域尚属空白,且本工程铁路与两侧建筑物的距离较近,因而难以确定其运行后对沿线建筑物的振动影响。针对这一问题,本文采用有限元和车辆-轨道耦合动力学理论,建立列车-轨道-单线双层框架桥-大地-建筑物三维耦合动力学模型,分析既有铁路改扩建后列车运行引起的振动对沿线建筑物的影响,相关研究成果可为既有铁路改扩建提供参考。
1 工程概况
某新建高速铁路利用既有铁路引入城区枢纽车站,需将区间单线铁路扩建为双线,同时综合考虑线路区间复杂工程,采用地面、地下单线双层框架结构实现既有铁路通达范围内增建1条铁路,上、下层线路轨面标高相差约9.0 m。为减少对既有建筑物的影响,框架桥边墙外侧设置围护墙,围护墙宽1.0 m,深13.0 m,底部坐落于弱风化泥质粉砂岩层中。框架桥空腔内部为下层铁路,地面为上层铁路,上、下层铁路道床均采用碎石道砟,线路运行CRH380系列动车组,8辆编组,路段限速80 km/h。扩建区段穿越城区,沿线居民楼等振动敏感建筑分布居多,最近距离为7.0 m,建筑结构形式包括砌体结构和框架结构,基础形式多为条形基础和独立基础,均坐落于软土层中。扩建区间横断面如图1所示,沿线建筑物情况统计如表1所示。

图1 扩建区间横断面示意图(m)

表1 建筑物情况统计表
2 动力计算模型
2.1 列车-轨道模型
基于车辆-轨道耦合动力学理论[5],建立列车空间动力学模型,通过列车-轨道分布式仿真平台[6]实现车辆运行行为的模拟,在轮轨接触模型中采用Hertz非线性弹性接触理论确定轮轨法向力:
(1)
式中:G——轮轨接触常数;
φZ(t)——轮轨之间的弹性压缩量(m)。
根据Kalker线性理论计算轮轨蠕滑力,然后采用沈式理论[7]进行非线性修正。
根据城市轨道交通轨道平顺性的特点及振动关注的4~200 Hz频段,本文采用铁道科学研究院提出的垂向短波不平顺的功率谱密度函数,可近似表达为:
S(f)=0.036f-3.15
(2)
式中:S(f)——不平顺的功率谱密度函数(mm2/(1/m));f是空间频率(1/m);其波长范围为0.01~1 m。
对于大于1.0 m波长范围的不平顺功率谱密度表达为:
(3)
式中:A、B、C、D、E、F、G——轨道不平顺功率谱密度的特征参数,对不同线路和不同类型的轨道不平顺有不同数值。
2.2 建筑物有限元模型
根据扩建区间建筑物的统计情况,建立4层砌体、4层框架、9层框架结构有限元模型。4层砌体结构层高3.0 m,基础形式为条形基础,埋深1.6 m,墙体为0.24 m厚砌体;4层框架结构层高3.0 m,基础形式为柱下独立基础,埋深2.0 m;9层框架结构第一层为车库,层高为2.2 m,2~9层为住宅,层高3.0 m,整体为现浇钢筋混凝土结构,基础为柱下独立基础,埋深3.0 m。有限元模型中构造柱、圈梁、框架梁、柱均采用梁单元模拟,楼板、墙体均采用壳单元模拟。
2.3 铁路-单线双层框架桥-大地-建筑物三维模型
大地模型采用实体单元模拟,整体模型尺寸沿轨道方向取200.0 m,垂直于轨道延伸方向取145.0 m,竖向取31.5 m,模型中包括单线双层框架桥,埋深7.5 m,地表以上部分2.0 m,围护墙贯穿软土层,伸入到强风化泥质粉砂岩中3.0 m。单向双层框架桥-大地-建筑物三维模型如图2所示,动力学模型土体计算参数如表2所示。土体网格尺寸受输入最短波长的限制,根据研究表明[8],网格尺寸须小于输入波形最短波长的1/8~1/10,且为能精确获得波动结果,单元尺寸应满足以下要求:

表2 动力学模型土体参数表

图2 单线双层框架桥-土体-建筑物三维模型图(m)
(4)
式中:Δx——模型网格划分单元尺寸;
Cs——土层的剪切波速(m/s);
fmax——分析时的上限频率(Hz)。
本文土体模型单元尺寸取0.15~3 m,在远离单线双层框架桥和建筑结构位置的土体网格逐渐放大,可满足计算的需要。
进行动力计算分析时,需在模型外围添加三维粘弹性人工边界[9],用来模拟模型以外的半无限空间土体,防止在边界上发生波的反射造成计算失真,人工边界等效为连续分布的并联弹簧-阻尼器系统,切向与法向的弹簧刚度和阻尼系数按照式(5)和式(6)取值:
(5)
(6)
式中:KBN、BBT——分别为弹簧法向与切向刚度;
CBN、CBT——分别为阻尼器法向与切向的阻尼系数;
R——波源至人工边界的距离;
cs和cp——分别为S波和P波波速;
G——介质剪切模量;
ρ——介质质量密度;
αT与αN——分别为切向与法向粘弹性人工边界修正系数,本文选取αT=1.33、αN=0.67。
动力分析中需要设定阻尼保证计算结果的准确性,本文中采用Rayleigh阻尼来计算,其假设结构阻尼矩阵是质量矩阵和刚度矩阵的组合,满足:
[C]=α[M]+β[K]
(7)
式中:[C]、[M]和[K]——分别代表体系的阻尼矩阵、质量矩阵和刚度矩阵;
α——质量阻尼系数,取α=2.46
β——刚度阻尼系数,取β=7.8e-5。
3 建筑物振动响应
基于构建的三维耦合动力学模型,考虑此扩建区间列车上、下层线路运行的实际情况,分别对3种工况条件下列车运行对建筑物的振动影响进行分析,列车运行工况如表3所示。建筑物测点的选取位置均为距线路中心相同的楼板跨中,建筑物测点布置如图3所示。

表3 列车运行工况表

图3 建筑物测点布置图(m)
3.1 峰值振动加速度
列车不同运行工况下建筑物各层测点峰值振动加速度如图4所示。从图4可以看出,当列车在此扩建区间内运行时,工况1的振动响应最小,工况3的振动响应最大,峰值振动加速度在建筑物首层出现最大值,在2~3层大幅度衰减,说明振动由底部向上部楼层传递时,在低楼层处会过滤大部分振动。从图4(a)和4(b)可以看出,振动在4层砖混结构内向上部传播时不断减小,在4层框架结构内向上部传播时先减小在顶层有放大现象,说明相同层高条件下框架结构随楼层的增加具有更强的振动传递性。从图4(c)可以看出,车致振动在9层框架内由底部向上部传播时,4~8层峰值振动加速度趋于一致,在顶部出现小幅度的增加。
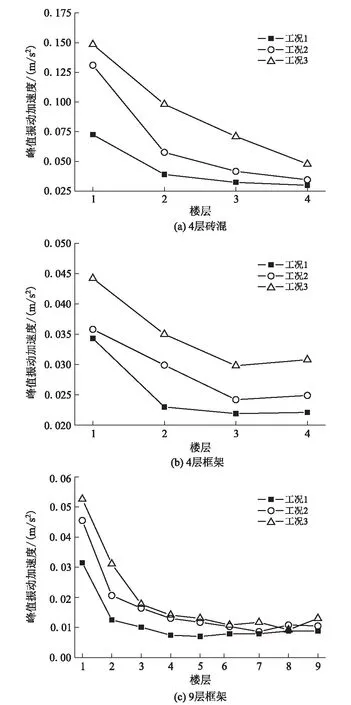
图4 建筑物测点峰值振动加速度图
3.2 振动加速度频域分析
4层砌体和框架结构建筑物首层测点不同工况下频域振动加速度如图5所示,因列车在大部分时间内为单一方向行驶,且工况2振动响应大于工况1,故对9层框架工况2的振动频域幅值进行研究,如图5(c)所示。

图5 建筑物测点频域振动图
从图5(a)和图5(b)可以看出,建筑物车致振动影响加速度幅值工况3明显大于工况1和工况2,但振动加速度频域分布规律基本一致;列车运行引起的振动对砌体结构的频域影响范围集中在50~70 Hz范围内,振动主频在60 Hz左右;列车引起的振动对框架结构的频域影响范围集中在30~70 Hz范围内,振动主频在58 Hz左右,由此说明振动对框架结构的频域影响范围更大,但加速度幅值更小。
从图5(c)可以看出,在工况2条件下,9层框架车致振动主频集中在40 Hz左右,但加速度幅值从2~4层大幅度减小,顶部趋于一致。振动随高度向上部的传播过程中大于60 Hz频率范围的加速度幅值衰减较快,4~20 Hz频率范围内的加速度幅值衰减缓慢,随着楼层的增加振动频率影响范围逐渐减小。
3.3 1/3倍频程振动加速度级
为确定列车运行引起的振动对建筑物楼板在频域上的分布,对车致振动响应进行1/3倍频程分析。列车在不同运行工况下建筑物测点的1/3倍频程振动加速度级如图6所示。工况2时4层砌体、框架首层测点1/3倍频程振动加速度级如图7所示。
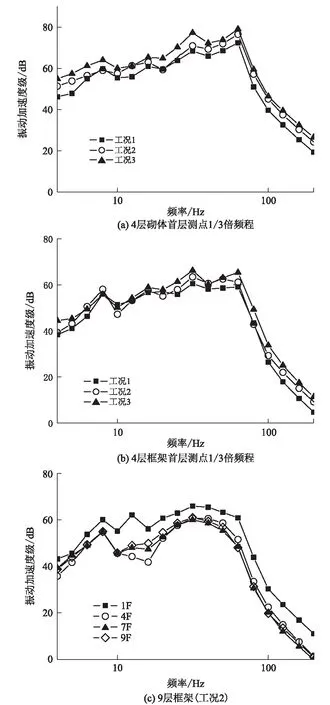
图6 建筑物1/3倍频程振动加速度级图

图7 4层砌体、框架首层测点1/3倍频程振动加速度级图(工况2)
从图6(a)可以看出,4层砌体结构首层测点在3种工况条件下振动加速度级峰值出现在8 Hz、31.5 Hz和63 Hz处,最大振级在63 Hz左右,工况3最大振级比工况2高 2.5 dB,比工况1高6.7 dB。从图6(b)可以看出,4层框架结构首层测点在3种工况条件下振动峰值主要出现在8 Hz、16 Hz、31.5 Hz和63 Hz处,最大振级出现在31.5 Hz左右,工况3最大振级比工况2高2.8 dB,比工况1高5.7 dB,工况2在8 Hz附近振级超过工况3。从图6(c)可以看出,工况2的9层框架首层测点振动加速度级在4~200 Hz频率范围内明显大于其他楼层约5 dB,楼板的振动加速度级峰值主要集中在31.5 Hz处,随着楼层的增加大于 60 Hz的振动有所衰减,4~20 Hz范围内的振动有所增加。
从图7可以看出,工况2砌体结构与框架结构的振动加速度级幅值变化趋势基本一致,在4~200 Hz频域范围内,层高相同、用途一致、距线路中心相同的砌体结构比框架结构振动加速度级平均高约10 dB。框架结构首层测点在8 Hz附近振动显著,此频段振动加速度级趋近于砌体结构首层测点。
通过上述分析可知,列车上、下层铁路同时运行引起振动对建筑物影响最大,上层线路运行引起的振动最小,下层线路运行引起的振动大于上层线路运行;建筑物首层测点1/3倍频程振动加速度级均在8 Hz与63 Hz频率左右出现峰值。振动加速度级在大于80 Hz的频率范围大幅度衰减。
4 建筑物振动评价
本文参考JGJ/T 170-2009《城市轨道交通引起建筑物振动与二次辐射噪声限制及其测量方法标准》[10]振动影响区域分类,选取2类区域进行铁路沿线建筑物的振动评价,其适用范围为居住、商业混住区,商业中心区,昼、夜间最大分频振动加速度级分别为70 dB和67 dB,既有沿线建筑物应当按照2类夜间标准控制。
建筑物各楼层测点分频最大振级随着楼层的变化如图8所示。从图8(a)可以看出,在相同的运行工况下,4层砌体建筑物各楼层分频最大振级比4层框架建筑物平均高约10.4 dB。3种工况4层砌体结构的分频最大振级均超出夜间限值,首层楼板的环境振动在工况1、工况2和工况3条件下分别超出夜间限值5.4 dB、9.6 dB、12.1 dB,分频最大振级随着楼层的增加,出现逐层衰减的现象,从首层至顶层衰减的程度达到4.7~7.4 dB;4层框架结构分频最大振级在3种工况条件下均未超出夜间限值,振动加速度级首层位置最大,随着楼层的增加,2、3层出现衰减,顶层的楼板呈现轻微的放大现象。

图8 建筑物3种工况下各楼层分频最大振级图
从图8(b)可以看出,9层框架分频最大振级在3种工况条件下均未超出夜间限值,各楼层测点分频最大振级从首层开始至5层减小达5.2~6.3 dB,6~9层出现小幅度的放大现象,放大幅值达到1.2~1.7 dB。
针对扩建区间列车运行对既有砌体建筑物振动超标的现象,有必要采取一定的减隔振措施,减小列车运行对既有砌体建筑物的影响,为后续既有线路的扩建改造提供指导意义。
5 结论
经由上述分析,可得到如下结论:
(1)列车以80 km/h的设计速度运行通过扩建区间,上、下层线路同时运行引起的振动对建筑物的影响最大,上层线路运行时对建筑物的影响最小,下层线路运行对建筑物的影响大于上层线路运行。
(2)列车运行引起的振动对距离线路中心相同的4层砌体影响大于4层框架,在相同运行工况下,砌体建筑物分频最大振级比框架建筑物平均高约10.4 dB。
(3)框架建筑物比砌体建筑物随楼层的增加具备更强的振动传递性,列车振动对砌体建筑物的影响从首层开始随着楼层的增加逐渐减小,对框架建筑物的影响从首层开始随着楼层的增加出现先减小后放大的现象。
(4)列车在扩建区间运行时4层、9层既有框架建筑物的环境振动均在夜间限值内,4层砌体建筑物的环境振动超出夜间限值,其首层楼板的环境振动在列车上层线路运行、下层线路运行、上层线路和下层线路同时运行时分别超出夜间限值5.4 dB、9.6 dB和12.1 dB,有必要采取一定的减隔振措施,减小列车运行对既有砌体建筑物的影响。

