A Novel Meshfree Analysis of Transient Heat Conduction Problems Using RRKPM

Hongfen Gao and Gaofeng Wei

1College of Intelligent Engineering,Shandong Management University,Jinan,250357,China

2School of Mechanical and Automotive Engineering,Qilu University of Technology(Shandong Academy of Sciences),Jinan,250353,China

3Shandong Institute of Mechanical Design and Research,Jinan,250353,China

ABSTRACT By introducing the radial basis functions (RBFs)into the reproducing kernel particle method (RKPM),the calculating accuracy and stability of the RKPM can be improved,and a novel meshfree method of the radial basis RKPM(meshfree RRKPM)is proposed.Meanwhile,the meshfree RRKPM is applied to transient heat conduction problems(THCP),and the corresponding equations of the meshfree RRKPM for the THCP are derived.The twopoint time difference scheme is selected to discretize the time of the THCP.Finally,the numerical results illustrate the effectiveness of the meshfree RRKPM for the THCP.

KEYWORDS Transient heat conduction;meshfree method;reproducing kernel particle method;meshfree RRKPM;two-point difference method

1 Introduction

Many practical engineering structures run in high temperature,such as steam turbines,highspeed diesel engines and nuclear power plants,etc.The temperature field can change the properties of material structure.Therefore,it is an important subject to study the THCP of the structure in the condition of being heated [1,2].

Numerical simulation is an important analysis tool to research the THCP [3].Finite element method (FEM) is one of the main numerical simulation methods.Many complex and difficult mechanical problems can be solved by the FEM,and valuable results can be derived [4,5].However,due to the limitation of the correlation conditions between elements in the FEM,it is difficult to deal with the discontinuous problem in practical engineering problems,such as the formation of cracks and their mechanical behavior,the discontinuity in jointed rock mass and the crack propagation with moving boundary [6,7].In order to improve the restriction of correlation conditions between elements,many novel methods have been proposed in recent years,such as meshfree (or meshless,element-free) method [8,9],numerical manifold method (NMM)[10–12],boundary element method (BEM) [13,14],and numerical method based on least square method [15–17],etc.

The meshfree approximating technique is adopted in the meshfree method,which makes the approximating function free from the constraints of elements and greatly simplifies the analysis and calculation of pretreatment and crack propagation.Meshfree method has attracted attention in mechanics and practical engineering,and been widely used in the study of the THCP.At present,many meshfree methods have been developed,such as smooth particle hydrodymics(Abbreviation: SPH,proposed by Lucyt and Gingold in 1977) [18,19],element-free Galerkin method (Abbreviation: EFGM,proposed by Belytschko in 1994) [20–22],meshfree local Petrov-Galerkin method (Abbreviation: MLPG,proposed by Atluri in 1998) [23–26],reproducing kernel particle method (Abbreviation: RKPM,proposed by Liu in 2005) [27–30],radial basis functions method (Abbreviation: RBF,proposed by Žilinskas in 2010) [31,32],complex variable meshfree manifold method (Abbreviation: CVMMM,proposed by Gao in 2010) [33],the finite point method (Abbreviation: FPM,proposed by Tatari in 2011) [34,35],Hermit-type reproducing kernel particle method (Abbreviation: Hermit-type RKPM,proposed by Ma in 2017) [36–39]and boundary integral equation method (Abbreviation: BIE,proposed by Mantegh in 2010)[40,41],etc.

Because of the advantages of simple form and fast calculation speed,the RKPM is one of the meshfree methods which are widely applied and researched [42–44].The RKPM is first proposed based on the SPH and the integral reconstruction theory of functions.The RKPM solves the boundary inconsistency,and eliminates the tensile instability of the SPH method.The method has some advantages,such as variable time frequency characteristics and multi-resolution characteristics.Therefore,the RKPM has been widely used in many practical engineering problems,such as large deformation analysis problems,structural dynamics problems,micro-electromechanical system analysis problems,nonlinear problem of hyperelastic rubber materials,high-speed impact problems and so on [45–47].

However,different kernel functions have different effects on the calculating accuracy and computational stability in the analysis of solving the THCP.In order to improve the calculating accuracy and stability of the RKPM,the RBF is introduced into the RKPM,and the meshfree RRKPM is proposed in this paper.Meanwhile,the meshfree RRKPM is applied to the THCP,and the corresponding equations of the meshfree RRKPM for THCP are derived.The numerical results illustrated the effectiveness of the meshfree RRKPM for the THCP.

2 Construction of the Approximating Function of Meshfree RRKPM

The approximating functionuh(z)of Meshfree RRKPM can be written as a combination of the RKPM constructed bynnodes in the local problem domain and the RBFs constructed bymterms.

wherecjandairepresent the undetermined coefficients,nrepresents the number of the local influence domain,mrepresents the number of RBFs,SmiandSnjrepresent the RBFs and the reproducing kernel function (RKF),respectively.

The RBFSmiis the function of the distancerifrom calculating pointzto the nodezi,ri=||z－zi||

withδdenoting the scaling parameter.

The RKFSnjcan be expressed as

whereSnj(zj)is the parameter of nodezj,ΔVjis the area or volume of domain of influence,wis kernel function.

The coefficient matrixb(z)can be given by

The polynomial basis functionp(z－zj)is expressed as

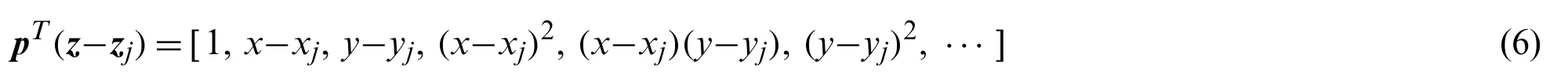
The Eq.(1) can be rewritten as the following form:

in whichSI(z)is basis function,aI(z)is corresponding coefficient,given by

The approximating functionuh(z)can be locally approximated in the neighborhood of calculating pointz

The weighted least squares method is used to obtain approximating functionsuh(z)accurately in this paper.The weighted least squares functionJis defined as

wherew(z－zK)is weighted function in the domain of influence,zK(K=1,2,···,N)are the nodes in the domain of influence.

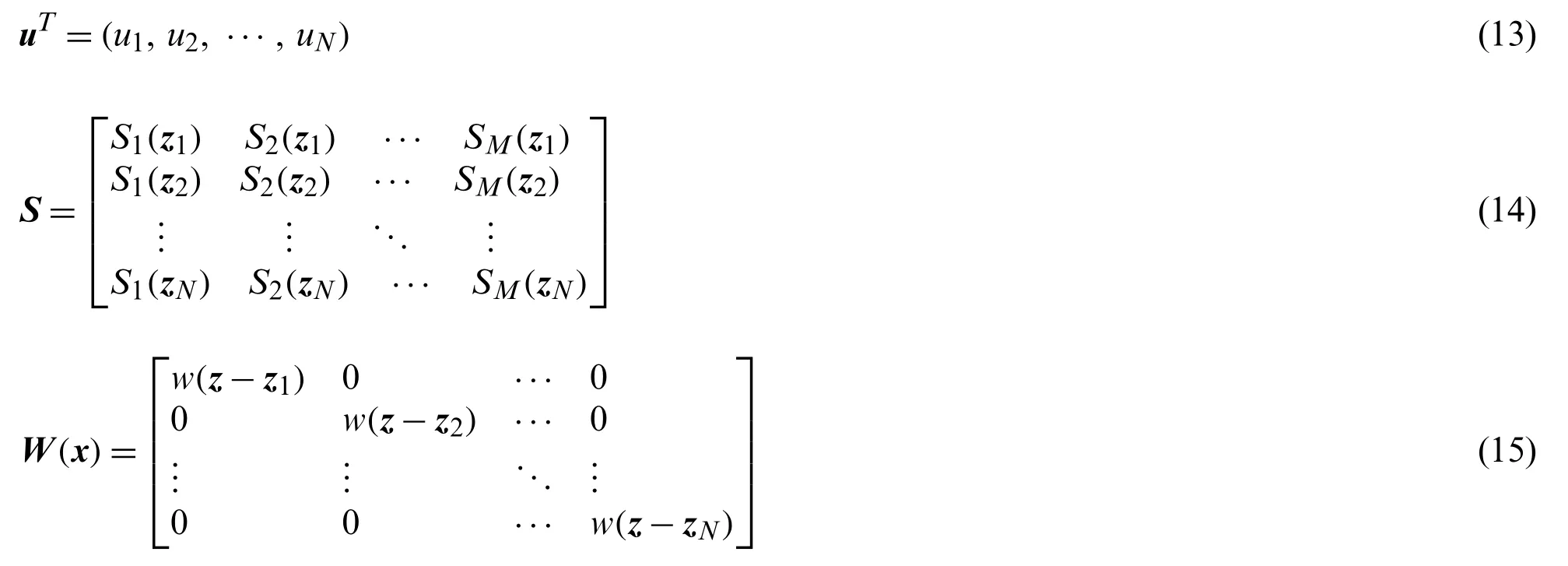
The Eq.(11) can be rewritten as the following form:

where

LetJtake the minimum,that is

The following form can be obtained

where

The Eq.(17) can be given as

Substituting Eq.(20) into Eq.(7),the approximating functionuh(z)is obtained

in which shaped functionΦ(z)is expressed as

3 Governing Equation of the THCP for Meshfree RRKPM

3.1 Fundamental Equations for the THCP

From the theory of transient heat conduction,the differential equation of THCP in orthotropic plane can be expressed as

whereT(z,t)represents transient temperature,tdenotes transient heat transfer time,kxandkyrepresent thermal conductivities of material in plane principal axes,ρrepresents density of material,cprepresents constant pressure specific heat andqvis internal heat source intensity.

The material is assumed to be isotropic withkx=ky=k,Eq.(23) can be simplified as

or

in whichαT=k/ρcprepresents thermal diffusivity,∇2denotes Laplace operator.

Assuming no heat source,the Eq.(25) is rewritten as the Fourier equation:

In order to obtain the unique solution of the THCP,boundary conditions and initial conditions must be applied.There are three kinds of boundary conditions as follows:

(1) The first kind of boundary condition is that the temperature on the boundary is known,and the formula is

or

in whichΓ1represents the boundary of first kind,(z,t)represents known boundary temperature (constant),f(x,y,t)represents known boundary temperature function which changes with time.

(2) The second kind of boundary condition is that the heat flux density on the boundary is known.Because the direction of the heat flux is the exterior normal direction of the boundary,the formula is as following:

or

whereΓ2represents the boundary of second kind of boundary condition,¯hrepresents known heat flux (constants),h(x,y,t)represents known heat flux function which changes with time.

(3) The third kind of boundary condition is that the convection or radiant heat transfer on the boundary is known.For convection heat transfer conditions

whereΓ3represents the boundary of third kind of boundary conditions,Trepresents temperature of fluid medium,grepresents heat transfer coefficient.

For radiant heat transfer conditions,it can be written as

withεrepresenting blackness coefficient,fdenoting shaped factor,σ0being Stefan-Bolzman constant andTr(z,t)representing temperature of radiant source.

The initial condition is the known value of the temperature at the beginning of the heat transfer process,and the formula is

or

From the heat conduction equation and boundary conditions,it can be seen that there is only one partial differential equation (PDE) and only one temperature as an unknown variable,therefore,the THCP is actually solving the PDE.

3.2 Integral Weak Form of the THCP

In a certain instantaneous state,T(z,t)andcan be considered as deterministic functions of plane coordinates.The THCP can be transformed to the elliptic equation of boundary value problem,and the formula is

The field function,which makes the variational of the functionΠequal zero,is the solution which satisfies the governing differential Eq.(23) and boundary condition of this problem.

Taking the first kind of boundary problem as an example,the temperature functionT(z,t)must satisfy the essential boundary condition (29),which isT(z,t)－(z,t)=0 on the boundaryΓ1,so the functionΠis conditional function.Introducing the penalty function method into the essential boundary conditions (28)–(32),and another modified functionΠ*can be constructed as

withβrepresenting penalty factor of generally 103～105in the THCP.After introducing essential boundary conditions,the conditional stationary value problem of original functionΠtransforms into the unconditional stationary value problem of modified functionΠ*.The first variation of the stationary condition for modified functionΠ*equals zero.

Substituting Eq.(36) into Eq.(38),the integral weak form of the THCP is

Everything went well for a week or a fortnight, and then the woman said, Hark you, husband, this cottage is far too small for us, and the garden and yard are little; the Flounder might just as well have given us a larger house. I should like to live in a great stone castle; go to the Flounder, and tell him to give us a castle. Ah, wife, said the man, the cottage is quite good enough; why should we live in a castle? What! said the woman; just go there, the Flounder can always do that. No, wife, said the man, the Flounder has just given us the cottage, I do not like to go back so soon, it might make him angry. Go, said the woman, he can do it quite easily, and will be glad to do it; just you go to him.

where

3.3 The Meshfree RRKPM for the THCP

The THCP is a function in space domainΩand in time domaint,and these two domains are not coupled.Therefore,the meshfree RRKPM and finite difference method (FDM) can be used to solve the problem,that is,the THCP is solved by the meshfree RRKPM in space domain and by the FDM in time domain.Firstly,the domainΩis discretized into a finite number of nodes,and then the temperature of any point in the domain at any timetis approximated by the node temperatureTI(t)in its influence domain.

It should be noted thatT(zI,t)of any field pointzin the domain is a scalar at any time,so the temperature can be given as

in whichΦ(z)represents a shaped function vector,which is just a function in the space domain.

and

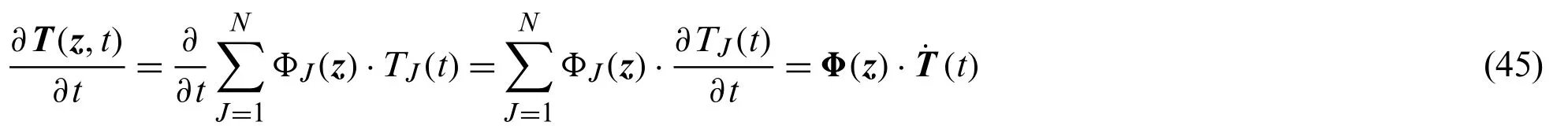
with

Substituting Eqs.(43),(45) and (47) into Eq.(39),the following form can be obtained:

The first term of Eq.(50) is

whereCrepresents heat capacity matrix,and can be expressed as

The second term of Eq.(50) is

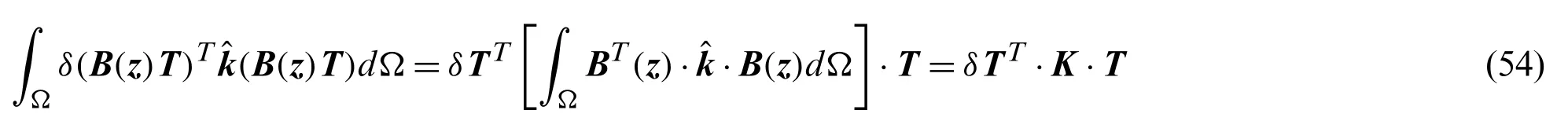
whereKrepresents heat conduction matrix

The third term of Eq.(50) is

The fourth term of Eq.(50) is

The fifth term of Eq.(50) is

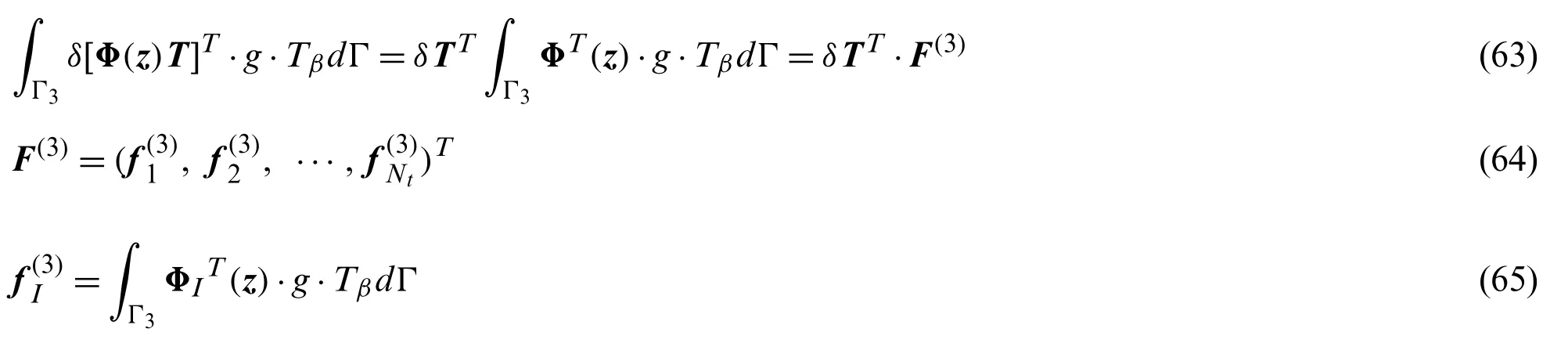
whereF(1),F(2)andF(3)represent thermal load vectors known as heat source,given heat flow and heat exchange,respectively.

The sixth term of Eq.(50) is

where

The seventh term of Eq.(50) is

where

The eighth term of Eq.(50) is

where

Substituting Eqs.(51),(54),(57),(60),(63),(66),(69) and (72) into Eq.(50),and the following form can be given:

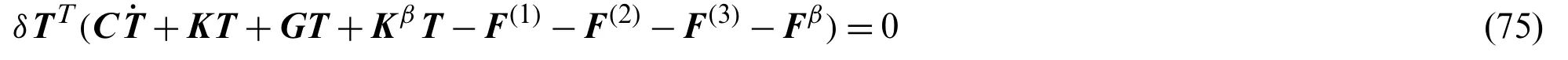
From the arbitrariness ofδTT,the final ordinary differential equations (ODE) can be given as

where

The PDE problems of the THCP have been discretized into initial value problems of the ODE with nodal temperatureT(t)in space domainΩ.

The above is the meshfree RRKPM for the THCP.

4 Time Integral Scheme

Eq.(76) is the linear ODE with timetbeing independent variable.In order to discretize the time domain of the ODE,the traditional two-point difference method is used in this paper.

In space domainΩ,the temperature vectorTis a function of timet,and can be divided into several elements.In any element,T(z,t)is given as

whereTi(t)=T(ti)represents nodal temperature vector at timeti.The interpolating functionNi(z)takes as same form for each component of the vectorT(z,t).

When the ODE only contains the first-order derivative of timet,the interpolate function is a linear polynomial,and the two-point first-order interpolation can be used.

For the time intervalΔt,T(z,t) can be obtained by interpolation of node valuesTn(t)andTn+1(t)in an interval

The first-order derivative ofT(z,t) is

The interpolate function and the first-order derivative can be expressed by the local variableλ

Using approximating interpolation of Eqs.(80) and (81),the Eq.(76) inevitably produces residual in a time intervalΔt.A weighted residual expression is derived as

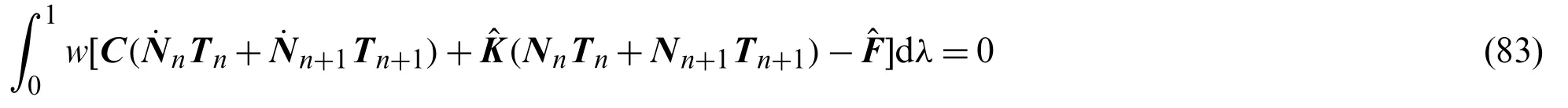
Substituting Eq.(82) into Eq.(83),the residual relation of two time intervals can be given as

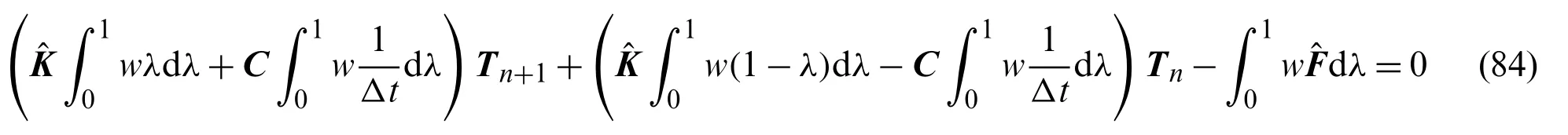
Eq.(84) can be seen as a general form applicable to any weighted function.

Substituting Eq.(86) into Eq.(85),the following form can be expressed

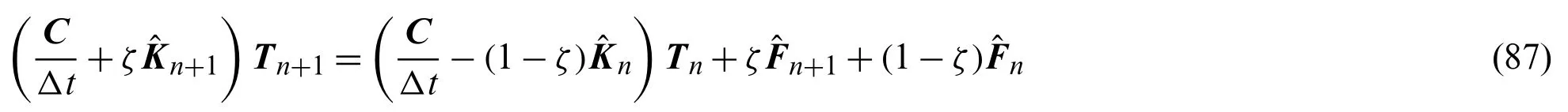
here

The above is the time difference scheme for the THCP.

5 Numerical Examples

5.1 Transient Temperature Field of the THCP in Rectangular Domain

The governing equation of the THCP in the rectangular domain is

According to the boundary conditions,written as

and the initial condition,given by

The analytical solution of the THCP can be obtained as

As shown in Fig.1,11×11 nodes are uniformly distributed in the rectangular THCP domainΩ,and time intervalΔt=0.001s.The penalty factor is taken asα=1.0×108and the scaling parameter is taken asδ=2.0.The regular quadrilateral background mesh is applied to the governing equation of THCP,and 4×4 Gauss integral scheme is used.

In order to discuss the influence of kernel functions on the calculation accuracy and stability,the kernel function is taken as the following two forms:

Figure 1:Distribution of nodes in rectangular domain for the THCP

In order to illustrate the validity of the proposed method,the temperature inx=0.5 and att=0.1 s is calculated by the analytical solution,RKPM and RRKPM,respectively.Fig.2 gives the comparison of the temperature between two methods using different kernel functions which the kernel function of Eq.(94) is defined as the kernel function 1 and the kernel function of (95)is defined as the kernel function 2.The relative error is defined as

whereTanalyticalis the analytical solution andTnumericalrepresents the numerical solution.

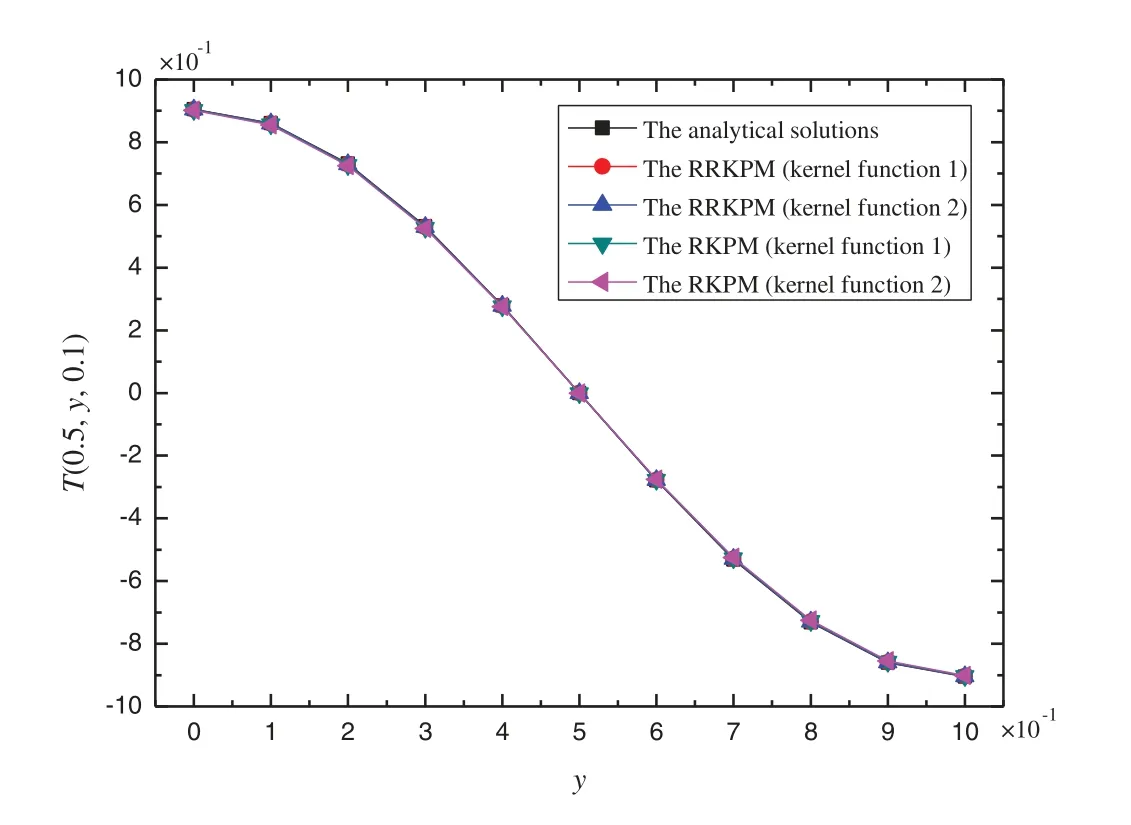
Figure 2:The temperature of the THCP for the RRKPM and the RKPM in x=0.5 and at t=0.1 s

Fig.3 discusses the relative error for the RRKPM and the RKPM,and it can be found that the maximum relative errors are 0.4518% and 0.4464% for the RRKPM,and 1.8054% and 1.2586% for the RKPM,respectively.The results illustrate that the RRKPM has better accuracy and stability than that of the RKPM.

Figure 3:The relative errors of the THCP for the RRKPM and the RKPM in x=0.5 and at t=0.1 s

Because the kernel function 1 has better accuracy than the kernel function 2,the kernel function 1 is used in the following analysis.Fig.4 compares the temperatures between the analytical solution and the RRKPM inx=0.5 and att=0.1,0.3,0.5,0.7,0.9 s,and it can be found that the solution of RRKPM agrees well with the analytical solution.

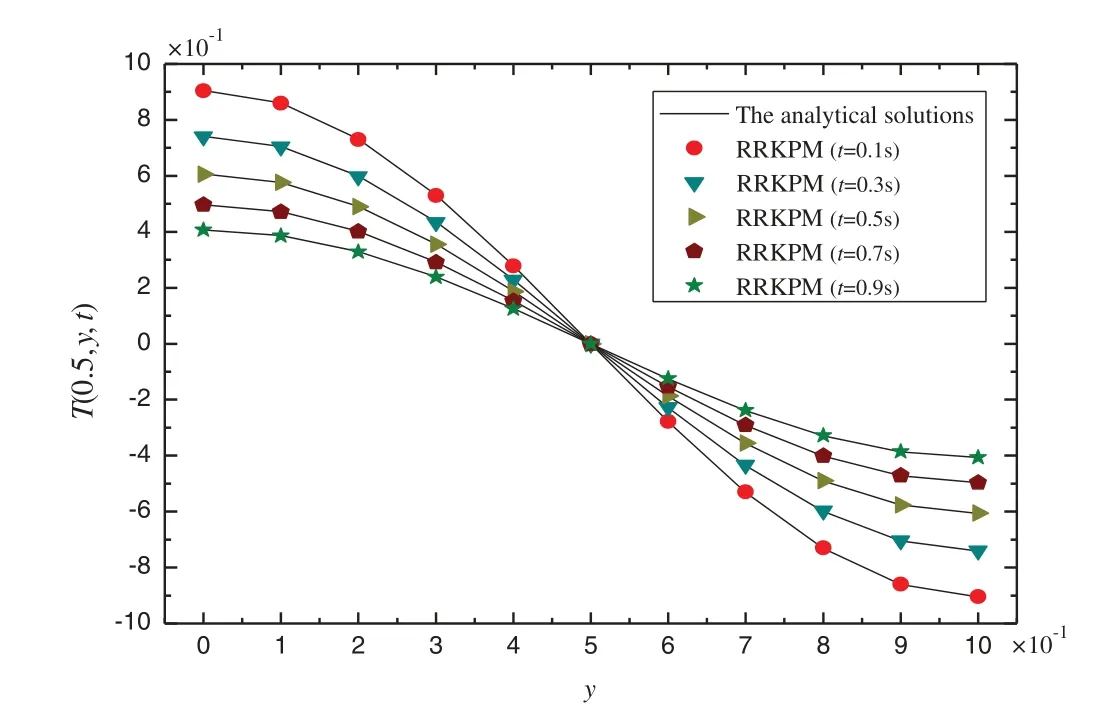
Figure 4:The temperature of the THCP for the RRKPM and the RKPM at different time in x=0.5

Fig.5 discusses the temperature among the analytical solution,the RKPM and the RRKPM iny=0.7 and att=0.1 s.Fig.6 analyzes the relative errors of the RKPM and the RRKPM.The maximum relative errors are 0.4400% and 1.8012% for the RRKPM and the RKPM,respectively,and it can be found that the RRKPM is in better agreement with the analytical solution.

Figure 5:The temperature of the THCP for the RRKPM and the RKPM in y=0.7 and at t=0.1 s

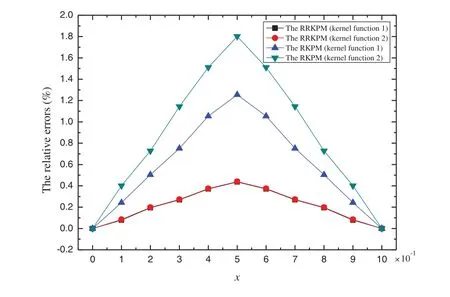
Figure 6:The relative errors between the RRKPM and the RKPM in y=0.7 and at t=0.1 s

Fig.7 compares the temperature between the analytical solution and the RRKPM iny=0.7 and att=0.1,0.3,0.5,0.7,0.9 s.The maximum relative error is 0.0795% for the RRKPM,and it can also be found that the RRKPM is consistent with the analytical solution.

The calculation results of the RRKPM are in better agreement with the analytical solutions,which shows that the calculation accuracy of the RRKPM is higher than that of RKPM.When different kernel functions are used for calculation,the calculated values of the RRKPM are consistent,but the RKPM has a large deviation.Meanwhile,the numerical results also show that the calculating accuracy of the RRKPM is not affected by kernel function,and its stability is better than that of RKPM.

Figure 7:The temperature for the RRKPM and the RKPM in y=0.7 at different time

5.2 Transient Temperature Field of the THCP in a Semi-Circular Ring Plate

The governing equation of the THCP in semi-circular ring plate is

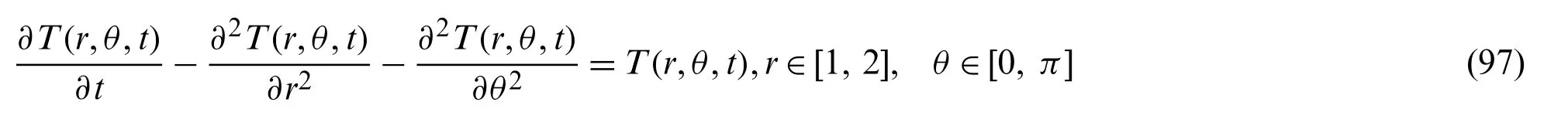
Based on the boundary conditions

and the initial condition

The analytical solution of the THCP is written as

Fig.8 is the node distribution in the THCP domainΩof the semi-circular ring plate with time intervalΔt=0.001s.The penalty factor is taken asα=1.0×108and the scaling parameter is taken asδ=2.0.

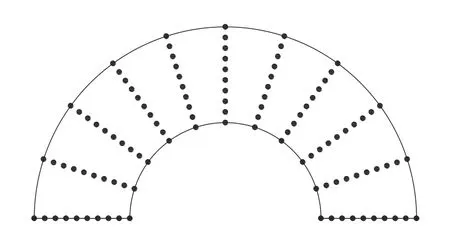
Figure 8:Node distribution in the semi-circular ring plate

The temperature inθ=π/4 and att=0.1 s is calculated by the analytical solution,the RRKPM and the RKPM,respectively (shown as Fig.9).In order to prove the effectiveness of the RRKPM,Fig.10 gives the relative errors of the RRKPM and the RKPM inθ=π/4 and att=0.1 s.It can be found from Fig.10 that the maximum relative error is 0.4421% for the RRKPM,and 1.7556% for the RKPM.The results illustrate that the RRKPM has a higher accuracy than the RKPM.

Figure 9:The temperature of the THCP for the RRKPM and the RKPM in θ=π/4 and at t=0.1 s

Fig.11 compares the temperatures between the analytical solution and the RRKPM inθ=π/2 and att=0.1,0.3,0.5,0.7,0.9 s.The maximum relative error is 0.4256% for the RRKPM,and it can be illustrated that the RRKPM is consistent with the analytical solution.

Fig.12 discusses the temperature among the analytical solution,the RKPM and the RRKPM inr=1.8 and att=0.1 s.Fig.13 analyzes the relative errors of the RRKPM and the RKPM.The maximum relative error is 0.4512% for the RRKPM,and 1.8179% for the RKPM,so the RRKPM agrees well with the analytical solution.

Fig.14 discusses the temperature among the analytical solution,the RKPM and the RRKPM inr=1.5 and att=0.1,0.3,0.5,0.7,0.9 s.The maximum relative error is 0.4186% for the RRKPM,and 1.7241% for the RKPM.It can be illustrated that the solution of RRKPM is consistent with the analytical solution.

Figure 10:The relative errors of the RRKPM and the RKPM for the THCP in θ=π/4 and at t=0.1 s

Figure 11:The temperature of the THCP for the RRKPM in θ=π/2 at different time

Figure 12:The temperature of the THCP for the RRKPM and the RKPM in r=1.8 and at t=0.1 s

Figure 13:The relative errors of the THCP for the RRKPM and the RKPM

Figure 14:The temperature of the THCP for the RRKPM and the RKPM in r=1.5 under different time

From above calculations,it can be shown that the calculation accuracy of the meshfree RRKPM is higher than that of the RKPM.When different kernel functions are used for calculation,the calculated values of the meshfree RRKPM are consistent,but the RKPM has a large deviation.So the numerical result of the meshfree RRKPM cannot be affected by the kernel function,and its stability is better than that of the RKPM.

6 Conclusions

A novel meshfree analysis of the RRKPM is developed for the THCP in this paper.The discrete governing equation of the THCP is established by the Galerkin weak form,and the corresponding equations of the meshfree RRKPM for the THCP are derived.From several examples of the THCP,it can be found that the meshfree analysis of the RRKPM has better calculating accuracy and convergence than that of the RKPM for solving the THCP.Meanwhile,the meshfree RRKPM can also be applied to many other interesting problems,such as complex structure dynamics,crack propagation and fracture,etc.These problems need to be further researched in the future work.

Availability of Data and Materials: The data and material used to support the findings of this study are available from the corresponding author upon request.

Authorship Contribution Statement: Hongfen Gao: Methodology,Software,Formal Analysis,Validation,Writing-Original Draft,Investigation.Gaofeng Wei: Conceptualization,Data Curation,Funding Acquisition,Writing-Review &Editing.

Acknowledgement: The first author is made possible through support from the Docking Industrial Collaborative Innovation Center of “Internet Plus Intelligent Manufacturing” of Shandong Universities.

Funding Statement: The first author is supported by the Natural Science Foundation of Shandong Province (Grant No.ZR2017MA028).The second author is supported by the Natural Science Foundation of Shandong Province (Grant No.ZR2020MA059).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.