基于数值预报与雷达外推预报融合方法的降水回波短临预报试验研究

王俊超，王志斌，赖安伟，2，肖艳姣，王 珏

（1. 中国气象局武汉暴雨研究所，暴雨监测预警湖北省重点实验室，湖北 武汉 430205；2. 中国气象科学研究院灾害天气国家重点实验室，北京 100081；3. 三峡国家气候观象台，湖北 宜昌 443000）

引 言

强对流天气（短时强降水、雷雨大风、龙卷风、冰雹）引发的洪涝和地质灾害给人民的生命安全与财产造成极大危害，对其进行临近预报预警意义重大。雷达外推预报和中尺度数值模式预报已成为目前短时定量降水临近预报关键技术支撑。雷达外推临近预报主要是对雷达回波的跟踪及外推。其中，交叉相关算法（tracking radar echoes by correla⁃tion，TREC）［1］是目前应用较为广泛的一种跟踪方法，通过计算相邻时刻雷达回波不同区域的最优空间相关性，确定回波的移动矢量特征，从而外推雷达回波未来时刻位置。随后，在TREC 算法基础上进一步改进，发展了COTREC（continuity of TREC vectors）［2］和DITREC（difference image based TREC）［3］等方法，并用于降水预报［4-5］。然而，TREC 及其扩展方法虽可以预报降水系统在未来时刻的位置，却无法预测其演变趋势，导致对强降水回波跟踪失败现象显著增加［6］。因此，后来又发展了局部光流法［7］与全局光流法［8］，通过计算雷达回波的光流场得到回波的运动矢量场，从而对雷达回波进行外推以达到预报目的。光流法可以弥补传统的交叉相关法缺陷，能够提升对流临近预报系统的性能［9-10］。近年来，循环神经网络模型广泛应用于天气雷达回波外推预报，并取得更为精确的外推效果［11］，同时还可以有效解决反射率因子预测问题［12］。此外，人工智能［13］和深度学习［14］方法的应用在强对流回波临近预报准确率上也有较明显提高。于是，基于以上短临预报技术发展了诸多短临预报系统［15-19］，并初步应用于预报业务中。

近年来，随着数值模式的发展，模式对各物理过程及其相互作用的描述越发精细，很多研究越来越注重结合观测资料评估模式的动力物理过程，尤其是云微物理过程。多普勒天气雷达观测资料具有很高的空间分辨率，能够在观测范围内捕捉到绝大多数类型的中小尺度天气系统。随着多普勒天气雷达布网，雷达资料在中尺度天气模式中的应用和研究逐步开展起来，发展了基于单部多普勒天气雷达资料反演大气三维风场和温度场的方法以及在中尺度天气模式初始场中同化雷达反射率和径向风资料的雷暴临近数值预报［20-25］。研究表明，利用雷达反射率调整模式初始场中云微物理变量能够有效改善中尺度数值模式的临近预报。尽管高分辨率的中尺度数值预报模式能够预报出对流系统的发展趋势，但由于模式预报在最初几小时始终存在“模式起转（spin-up）”问题，导致最初几小时内预报结果不甚理想，无法直接应用于短时临近预报。

雷达外推预报和数值模式预报各有所长，将二者融合可以提高临近（0~6 h）预报能力。因此，基于数值模式和雷达外推预报的融合降水预报迅速发展［26-27］，通过融合雷达回波外推和数值预报降尺度结果，获得多尺度定量降水预报概率，并设置雷达外推产品和模式产品的最佳时间变化曲线来最优化融合结果，得到与雷达外推临近预报水平相似的校正模式预报场。主要的融合预报系统包括：澳大利亚的STEPS（short-term ensemble prediction system）［28］、加 拿 大 的ARMOR（adjustment of rain from models with radar）［29］、奥 地 利 的INCA（inte⁃grated nowcasting through comprehensive analy⁃sis）［30］、英 国 的NIMROD（nowcasting and initializa⁃tion for modeling using regional observation data scheme）［26］以 及 中 国 香 港 的RAPIDS（rainstorm analysis and prediction integrated data-processing sys⁃tem）［31］、广东省的GRAPES-SWIFT（severe weather integrated forecasting tools）［32］等系统。RAPIDS 系统在临近预报结果基础上，通过融合数值预报结果，克服了临近预报系统的预报时效问题和数值预报的“起转”问题，从而提高0~6 h 的定量降水预报效果，特别是降水强度预报准确率的提高。2008 年北京奥运会对上述临近预报系统能力进行验证，发现融合预报系统的预报效果总体优于单一的雷达回波外推预报。

为提高数值模式对对流尺度定量降水短时预报能力，弥补雷达外推临近预报技术在2 h 以上定量降水预报能力不足，本文在前人研究基础上，基于中国气象局武汉暴雨研究所短时临近预报和武汉高分辨率快速更新循环预报系统（rapid update cycle，RUC）模式预报产品，设计多尺度雷达回波融合技术方案，进行降水预报试验，并对预报结果进行评估检验，以期提高中尺度对流天气短临预报业务成效。

1 试验数据

1.1 雷达回波外推预报

雷达回波外推预报是根据雷达先前几个时刻和当前时刻观测的回波图像，计算回波的移速和移向，并依据移速和移向外推预告未来时刻回波位置。针对强对流天气，采用改进的变分光流法［33］，对雷达数据进行风场反演，计算回波光流场变化以获得运动矢量场。改进的变分光流法是将局部光流法与全局光流法通过一个能量函数有机结合起来，并加入高阶平滑算子，求解方程得到流场结构后，再运用9点滑动平均得到运动矢量场，最后采用semi-Lagrange方法进行外推预报。

为满足实际业务需求，采用共享内存方式并行处理生成雷达回波外推预报产品，提供每6 min 滚动更新的0~3 h 逐小时雷达回波外推格点预报，格点分辨率为0.01°× 0.01°。其中，并行处理方法采用Fork-Join 模式，即在处理多部雷达资料时，把单部雷达资料派生到各个独立的CPU 上进行处理，各自独立生成三维格点场，最后做拼接处理，其加速比可达5.05［34］。

1.2 中尺度数值模式预报

为提高灾害性天气短时预报能力，2019 年中国气象局武汉暴雨研究所围绕3DVAR 同化雷达反射率因子来修正水汽不足问题，构建“伪水汽”观测同化方案，从而改善对流尺度系统水汽条件、减弱模式spin-up 问题［35］，进而改进0~3 h 降水预报，同时实现本地化运行。因此，在曙光高性能计算机上搭建1.5 km 水平分辨率、15 min 分析更新频率、1 h 预报更新频率、0~12 h 预报时效的对流尺度快速更新循环预报系统（简称“武汉RUC”），模拟区域中心为113.0°E、30.5°N，水平格点数801×701，垂直方向51 层。该数值预报系统主要包括：观测资料预处理系统、模式前处理系统WPS4.0、资料同化系统ARPS 3DVAR、模式系统WRF3.7.1、模式后处理系统UPP4.0。模式预报产品主要包括降水量、雷达回波、风场、涡度、上升螺旋度等强对流指示变量。

2 融合预报关键技术

借鉴香港天文台RAPIDS 技术思路，基于傅里叶-梅林变换和威布尔分布，以雷达实况为基准，实现雷达回波模式预报相位和强度校正方法，并结合多尺度光流变分法（multi-scale optical flow by varia⁃tional analysis，MOVA）［36］的雷达回波外推预报，采用双曲正切函数，对雷达回波外推预报和校正后的雷达回波模式预报进行融合，初步实现对武汉RUC 0~3 h雷达回波预报的融合，技术流程见图1。

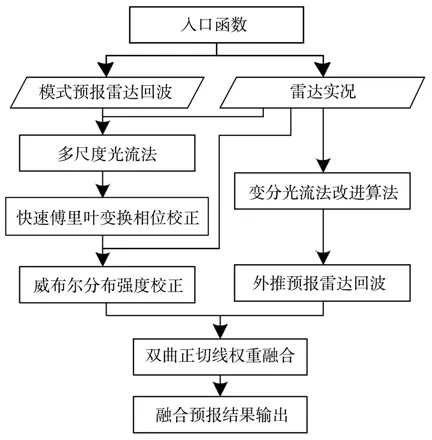
图1 数值预报与雷达回波短临外推预报融合技术流程Fig.1 The blending technology flow chart of numerical prediction and short-term and impending extrapolation prediction of radar echo

2.1 模式预报的雷达回波相位校正

数值预报雷达回波相位校正分两步：首先，利用傅里叶-梅林变换对模式预报的雷达回波场整体旋转角度和位移偏差进行修正；其次，采用MOVA方法校正局部区域位置误差（相位误差），使雷达回波雨带走向和小范围回波区得到合理调整。

2.1.1 基于傅里叶-梅林变换的相位校正

傅里叶-梅林变换是快速傅里叶变换和对数极坐标变换的全局相位相关。首先，将同一时刻雷达回波实况场和模式预报场以零频率分量为中心进行傅里叶变换，利用高通滤波器计算傅里叶变换的幅度谱，将高通傅里叶变换相位转换为对数极坐标空间；然后，将对数极坐标的幅度进行傅里叶逆变换，通过计算二者的交叉功率谱，找到相位相关的峰值计算模式预报场的旋转角度；最后，对角度方向进行判断，确定最终旋转角度及位移偏差，从而实现对模式预报雷达回波的相位校正。其平移和旋转特性处理方法见图2。（1）雷达回波场平移特性处理

图2 快速傅里叶变换相位校正平移（a）和旋转（b）特性算法流程Fig.2 The proess of translation（a）and rotation（b）characteristics algorithm of phase correction by fast Fourier transformation

空域中的平移在频域中只反映在相位变化。假设雷达回波场f2(x，y)是雷达回波场f1(x，y)经平移(x0，y0)后得到，即f2(x，y)=f1(x-x0，y-y0)，F1(u，v)和F2(u，v)分别为f1(x，y)和f2(x，y)的傅里叶变换，对其归一化后计算频域交叉功率谱。定义F*2(u，v)为F2(u，v)的共轭函数，对交叉功率谱进行逆变换可得到二维冲击函数。计算公式如下：

式中：i 为虚数；x、y表示雷达回波场空间坐标；x0、y0为空间坐标平移量；u、v为雷达回波场频谱坐标。二维冲击函数δ(x-x0，y-y0)在(x0，y0)位置处有明显的尖锐峰值，而其他位置值接近于0，据此求得2个雷达回波场的偏移量。

（2）雷达回波场旋转特性处理

若雷达回波场f2(x，y)是雷达回波场f1(x，y)经平移(x0，y0)、旋转α角度后得到，其公式表示为：

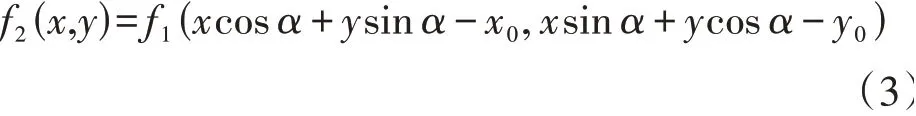
根据傅里叶变换旋转和平移特性，经变换后2个雷达回波场的关系可表示为：

假定M1(u，v)、M2(u，v)分别表示F1(u，v)、F2(u，v)的能量，则：

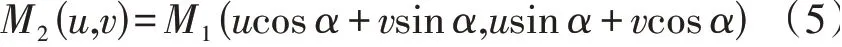
由公式（5）可见，M1(u，v)是M2(u，v)旋转α角度后得到，直角坐标的旋转对应极坐标的角度平移，因此利用相位相关理论可求得α值。

2.1.2 MOVA区域相位校正

多尺度光流变分法基于变分法及光流场平滑化算法进行定量降雨预报。光流是空间物体在平面上投影运动的速度，将光流矢量定义为投影平面特定坐标点上运动变化趋势，以矢量场(u′，v′)表示，求解这2 个独立变量，需要引入附加约束条件。将光流方程基本误差函数定义为J0，利用拉普拉斯算子表示平滑化约束条件项Js，γ为附加约束的拉格朗日乘子，基于光流准则和运动平滑性准则定义总误差目标函数J2，J为极小化问题的总误差，计算公式如下：

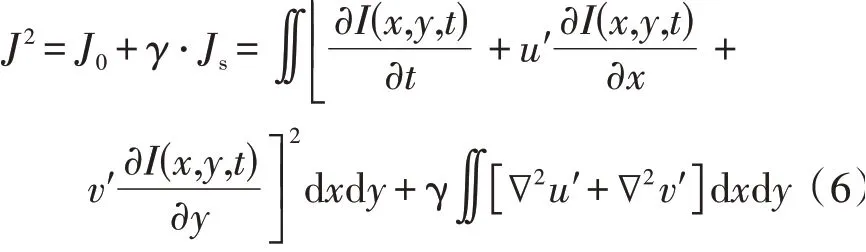
式中：I(x，y，t)为数值模式预报的逐小时雷达回波。将雷达回波数据以不同分辨率从低到高分为7 层，并逐一解算相应光流场。在不同层级光流分析中，由于设定的尺度和分辨率不同，平滑化约束项γ也不相同，且γ值随层级升高而增大，表明平滑作用在小尺度上愈加重要。利用MOVA 分别求解不同尺度（分辨率）的光流方程，得到最优的光流场解，从而获得不同尺度（分辨率）下雨带的运动矢量；然后，通过求算同时刻傅里叶变换后的回波模式预报场和实况场的误差平方最小值获得雷达回波预报场最佳平移位置，进而得到相位校正矢量场(u′，v′)，并将其应用于下一时次预报场校正中，最终实现模式预报雷达回波场局部区域相位调整。

2.2 模式预报的雷达回波强度校正

数值模式预报的雷达回波强度与实况的差异可能由模式分辨率及对流参数化和云微物理方案等物理过程造成。强度订正是通过将模式预报的雷达回波场逐步向定量估测降水场逼近来调整。

统计发现，模式预报的雷达回波和实况均满足威布尔分布，且二者的概率密度分布函数相同。分布函数F(x)及概率密度分布函数f(x)可表示为：

式中：α、β分别为形状参数和尺度参数，取值均大于0；a0为位置参数，其值小于xmin，由于模式预报的雷达回波范围及分辨率与外推雷达回波预报相同，因此a0取值为0，分布函数仅与α、β参数有关。每次运行时，通过多样本运算求解，得到威布尔分布的参数α和β。试验发现，不同分辨率、不同时次雷达回波的威布尔分布形状参数和尺度参数各不相同，故而需要对每一时次回波强度进行校正。模式预报雷达回波强度校正If-mod模型如下：

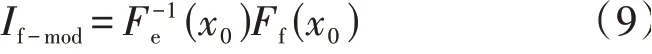
式中：Ff(x0)和Fe(x0)分别为模式预报和雷达外推预报的雷达回波初始时刻累积分布函数。

2.3 雷达外推预报和模式订正预报融合

对数值模式预报的雷达回波进行落区和强度订正并按时间序列调整后，结合雷达外推预报方法优化，对二者进行融合处理［37］。模式预报的权重变化用双曲正切函数表示［38］，其经验方程如下：

式中：t为时间；a和b分别为1 h和6 h模式预报的融合权重，权重可以根据雷达回波特征和降水演变特征历史统计结果确定，也可以结合位置误差和强度误差来动态指定［39］；k为融合时段中间部分W(t)的斜率，其值可根据天气类型和雷达反射率的谱空间相关性等确定，通过调节k值确定权重曲线的变化快慢。融合预报计算公式如下：

式中：RRUC(t)、RRFST(t)和Rblending(t)分别表示t时刻武汉RUC模式预报、雷达外推预报和融合预报。

3 个例试验及检验

3.1 个例试验

在实际业务中，为避免相位频繁调整导致的差错，需要根据设定的相位阈值进行试验参数调整，以提高相位调整效果。误差分析是基于格点的，不同空间尺度（分辨率）的预报误差不同，因此需要分析预报误差与尺度间的关系。利用上述3 种方法，对湖北省2020 年6—7 月4 次降水个例（简称“6·12”、“6·27”、“7·02”、“7·05”过程）强降水时段（表1）进行0~3 h 多尺度不同回波阈值的降水回波预报试验，空间尺度分别为0.01°× 0.01°、0.02°×0.02°、0.04°×0.04°和0.08°×0.08°，回波阈值分别为10、20、30、40 dBZ。其中，0.02°× 0.02°、0.04°×0.04°和0.08°×0.08°尺度是通过0.01°×0.01°尺度等间隔取样获取。

表1 湖北省2020年6—7月4次降水过程的强降水时段Tab.1 The occurrence period of heavy precipitation during four precipitation processes from June to July 2020 in Hubei Province

3.1.1 “6·12”过程

2020 年6 月12—14 日，受高空槽东移影响，湖北省出现入梅以来首场区域性暴雨过程，强降水中心位于江汉平原东南部及恩施东部，雨带呈东北—西南向。此次过程暴雨覆盖范围广、强度大，境内国家站共出现29 站次暴雨和7 站次大暴雨，荆门、荆州、恩施、宜昌、黄冈等地共62个区域站小时雨量达50 mm 以上，并伴有大范围雷电和局部8~9 级雷暴大风。其中，全省有2 市大暴雨（武汉104 mm、麻城101 mm）、18 县（市）暴雨、19 县（市）大雨；乡镇有68 站大暴雨、482 站暴雨，雨量最大为公安闸口195 mm，小时雨量最大为红安陡山86 mm。此次暴雨过程造成荆州、恩施等地严重受灾，给当地农业、人民生产生活等造成不利影响。

图3是2020 年6 月12 日12：00（世界时）起报的1 h 不同尺度降水回波雷达外推预报、武汉RUC 模式预报及融合试验与实况的对比。整体来看，预报的降水回波主体区域基本都集中在荆州、咸宁、武汉一带，位置相对未变，与实况相吻合。对比发现，武汉RUC 模式对强回波中心位置预报效果明显好于雷达外推预报，但预报强度偏小，而融合预报结果改善了雷达外推预报强降水位置偏差及模式预报强度偏差问题，总体效果优于单一的数值模式预报和雷达外推预报。

图3 2020年6月12日12：00起报的1 h不同尺度降水回波的雷达外推预报（a、e）、武汉RUC模式预报（b、f）、融合预报（c、g）与实况（d、h）对比（单位：dBZ）（红色方框为强降水集中区域。下同）（a、b、c、d）0.01°×0.01°，（e、f、g、h）0.02°×0.02°Fig.3 Comparison of 1-hour precipitation echo forecast with different scales from radar extrapolation（a，e），RUC-Wuhan model（b，f）and blending technology（e，g）initiated from 12：00 UTC 12 June 2020 with the observation of radar（d，h）（Unit：dBZ）（The red box represents the intensive region of heavy precipitation. the same as below）（a，b，c，d）0.01°×0.01°，（e，f，g，h）0.02°×0.02°

3.1.2 “7·05”过程

2020 年7 月湖北省平均降水量为437.1 mm，较常年同期偏多1.1倍，位列1961年以来同期第一位。其间，强降水过程频繁，出现2次区域性大暴雨过程和3次区域性暴雨过程，多站日降水量、持续降水量突破历史极值，强降水反复出现在鄂西南中西部、江汉平原南部及鄂东地区。其中，4—8日过程为当年梅雨期最强降水过程，达特强（I级）等级，强降水出现在鄂西南—江汉平原—鄂东一线，中心位于鄂东东部，共出现62站次暴雨、39站次大暴雨、2站特大暴雨，且19站暴雨日达3~5 d，鄂东中东部接连出现暴雨和大暴雨，大冶、浠水连续5 d出现暴雨或大暴雨，黄梅日降水量［7日08：00至8日08：00（北京时），331.9 mm］突破历史极值。此次过程，国家站和区域站分别有5 站和89 站小时雨量达50 mm 或以上，最大值分别为蔡甸站75.9 mm、应城长江埠93.5 mm，综合雨强在历年湖北省特强区域性暴雨过程中排第5位。

图4是2020 年7 月5 日16：00（世界时）起报的1 h 多尺度降水回波雷达外推预报、武汉RUC 模式预报及融合试验与实况对比。可以看出，实况降水回波主要集中在荆州、仙桃、武汉一带，雷达外推预报在降水回波位置上对应比较准确，但强度偏小，而模式预报在降水回波位置和强度上都有偏差；通过威布尔分布调整模式预报强度，并在0~1 h 融合预报中赋予雷达外推预报较大权重，利用双曲正切线将外推预报和模式预报进行融合，其结果总体优于单一的数值预报和外推预报。

图4 2020年7月5日16：00起报的1 h不同尺度降水回波的雷达外推预报（a、e）、武汉RUC模式预报（b、f）、融合预报（c、g）与实况（d、h）对比（单位：dBZ）（a、b、c、d）0.01°×0.01°，（e、f、g、h）0.04°×0.04°Fig.4 Comparison of 1-hour precipitation echo forecast with different scales from radar extrapolation（a，e），RUC-Wuhan model（b，f）and blending technology（e，g）initiated from 16：00 UTC 5 July 2020 with the observation of radar（d，h）（Unit：dBZ）（a，b，c，d）0.01°×0.01°，（e，f，g，h）0.04°×0.04°

3.2 预报效果检验

3.2.1 预报技巧评分

采用国际上常用的ETS（equitable threat score）和Bias 预报技巧评分方法对上述4 次降水个例进行预报效果检验。考虑风的影响，会有1~2 个格点的空间预报误差。因此，评估过程是对降水回波预报场每个格点（分辨率为0.01°×0.01°，约1 km×1 km）及周围相邻的3×3格点区域平均值与该格点观测回波进行对比。ETS 和Bias的计算公式如下：

式中：R为随机观测指数；a、b、c分别为降水回波预报正确、空报和漏报的格点数，d为无降水预报正确的格点数。Bias 越接近1，说明预报范围越接近实况；Bias大于1，说明预报范围较实况偏大；Bias小于1，说明预报范围较实况偏小。

图5是4 次降水个例不同阈值降水回波预报的平均Bias 随预报时效变化。可以看出，RFST、武汉RUC 预报和融合预报偏差随降水类型（回波强度）不同差异较大，但总体上预报范围均偏小，RFST 和融合预报效果明显优于RUC 模式预报；随着回波强度阈值增大，0~1 h 融合预报和武汉RUC 预报与实况范围的偏差逐渐缩小，而RFST 预报偏差逐渐增大，其他预报时效3 种预报与实况的偏差均逐渐增大；各回波阈值武汉RUC 模式预报与实况范围偏差均随预报时效增加明显增大，而RFST 预报和融合预报对于低阈值（10 dBZ 和20 dBZ）回波的预报偏差随预报时效增加变化不明显，而对于高阈值（30 dBZ 和40 dBZ）回波的预报偏差则随预报时效增加呈先增后降趋势。从预报效果来看，对于30 dBZ 及以上降水回波，融合预报效果明显好于其他2 种预报，特别是40 dBZ 及以上强回波0~1 h融合预报平均Bias接近1；对于弱回波（10~20 dBZ），RFST 预报效果略好于融合预报，其原因是经快速傅里叶变换，相位调整后的模式预报雨区在原位置有少许降水残留，导致10 dBZ 阈值下出现过多的弱降水空报现象。

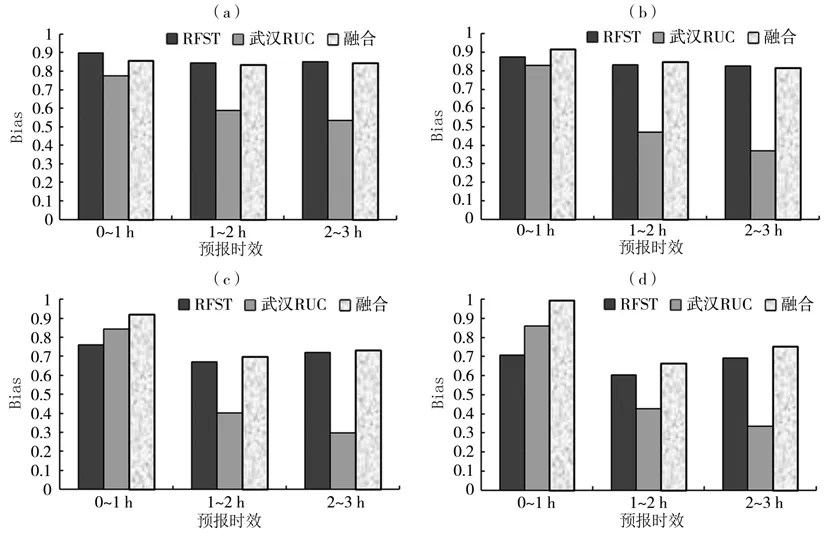
图5 4次降水过程不同阈值3种方法降水回波预报的平均Bias随预报时效变化（a）10 dBZ，（b）20 dBZ，（c）30 dBZ，（d）40 dBZFig.5 The change of average Bias of precipitation echo prediction by three methods for different thresholds with prediction time for four precipitation processes（a）10 dBZ，（b）20 dBZ，（c）30 dBZ，（d）40 dBZ

图6是4次降水过程不同尺度0~1 h降水回波预报的平均Bias随阈值变化。可以看出，0.01°×0.01°尺度，武汉RUC 模式预报和融合预报的降水回波平均Bias 随阈值增大呈先升后降趋势，30 dBZ 阈值的预报范围与实况最接近，而雷达外推预报的平均Bias 随阈值增加而减小，10 dBZ 阈值的预报范围较实况偏大，随着阈值增加预报范围较实况偏小且偏差越来越大，3 种方法的平均Bias 在0.76~1.03 之间；其他尺度，武汉RUC 模式预报的平均Bias 随阈值增加而增大，除10 dBZ 阈值的回波范围预报较实况偏小外，其他阈值均较实况偏大，而雷达外推预报和融合预报的平均Bias则随阈值增加呈先升后降趋势，20 dBZ 阈值的范围预报与实况最接近。总体来看，0.01°×0.01°尺度3种方法预报效果均优于其他尺度；对于40 dBZ及以上强回波，不同尺度融合预报的回波范围与实况最接近，而对于20 dBZ 以下弱回波，不同尺度的融合预报效果低于雷达外推预报。

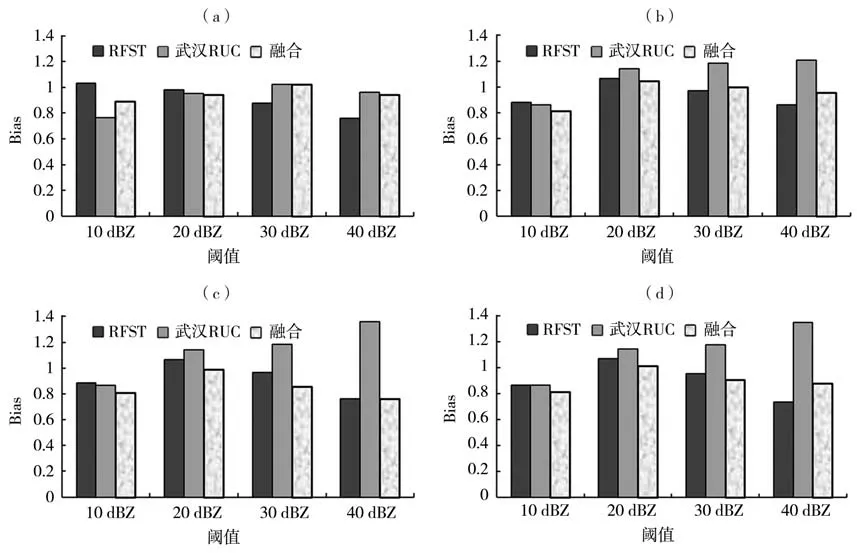
图6 4次降水过程不同尺度3种方法0~1 h降水回波预报的平均Bias随阈值变化（a）0.01°×0.01°，（b）0.02°×0.02°，（c）0.04°×0.04°，（d）0.08°×0.08°Fig.6 The change of average Bias of 0-1 h precipitation echo prediction by three methods for different scales with thresholds for four precipitation processes（a）0.01°×0.01°，（b）0.02°×0.02°，（c）0.04°×0.04°，（d）0.08°×0.08°

由于Bias 无法反映降水回波位置的预报效果，需综合ETS 评分才能够较全面地评估降水预报性能。前面分析可知，就回波范围预报，雷达外推预报和融合预报效果明显好于模式预报，因此图7 给出4次降水过程不同阈值下雷达外推预报和融合预报的平均ETS 评分随预报时效变化。可以看出，RFST 预报与融合预报的平均ETS 评分随回波强度和预报时效增加而减小，尤其是30 dBZ 及以上降水回波，其ETS 评分明显减小，ETS 评分低于0.5。总体来看，40 dBZ 及以上降水回波位置融合预报效果明显优于RFST 预报，与Bias 结果相吻合，这表明融合技术在强降水回波预报中有明显优势，对对流预报有积极作用。

图7 4次降水过程不同阈值2种方法降水回波预报的平均ETS评分随预报时效变化（a）10 dBZ，（b）20 dBZ，（c）30 dBZ，（d）40 dBZFig.7 The change of average ETS scores of precipitation echo prediction by two methods for different thresholds with prediction time for four precipitation processes（a）10 dBZ，（b）20 dBZ，（c）30 dBZ，（d）40 dBZ

从4 次降水过程不同尺度0~1 h 回波预报的平均ETS 评分随阈值变化（图8）看出，同一尺度，各方法的ETS 评分随回波阈值增加呈先升后降趋势（0.01°×0.01°尺度的RFST 预报除外），20 dBZ 的回波阈值对降水位置预报效果最好，40 dBZ 的回波阈值对降水位置预报偏差最大，0.01°×0.01°和0.02°×0.02°尺度的融合预报对降水位置预报效果明显好于单一预报，而0.04°×0.04°和0.08°×0.08°尺度的融合预报差别不明显，且与RFST 预报效果相近。对比发现，武汉RUC 模式的降水位置预报ETS 评分最低。

图8 4次降水过程不同尺度3种方法0~1 h降水回波预报的平均ETS评分随阈值变化（a）0.01°×0.01°，（b）0.02°×0.02°，（c）0.04°×0.04°，（d）0.08°×0.08°Fig.8 The change of average ETS scores of 0-1 h precipitation echo forecast by three methods for different scales with thresholds for four precipitation processes（a）0.01°×0.01°，（b）0.02°×0.02°，（c）0.04°×0.04°，（d）0.08°×0.08°

综合Bias 和ETS 评分得出，0.01°× 0.01°尺度的预报效果明显好于其他3 个尺度，原因可能是随尺度增大其插值结果在边界上的误差逐渐增大，这有待后续进一步深入研究。

3.2.2 平均绝对误差和命中率

预报技巧评分无法直观给出预报准确率，因此选取平均绝对误差（mean absolute error，MAE）和命中率（probability of detection，POD）2 个指标来描述预报准确率。计算公式如下：式中：N为格点数；yi、y′i（dBZ）分别为回波预报值和观测值。

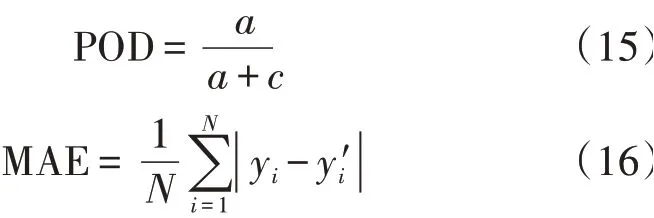
图9是4 次降水过程不同阈值融合预报的POD和MAE 随预报时效变化。可以看出，不同过程预报误差不同，POD 随阈值和预报时效增加而降低，2 h 预报时效内10 dBZ 回波阈值的POD 均高于0.545，而MAE 随阈值和预报时效变化不大，波动范围在2 dBZ 以内，如“6·12”过程10 dBZ 阈值的0~1 h预报时效POD 为0.674、相应的MAE 为6.3 dBZ，即0~1 h 融合预报有67.4 %的降水范围预报正确，总体平均绝对误差是6.3 dBZ。

图9 4次降水过程不同阈值融合预报的平均POD（a、b、c、d）和MAE（e、f、g、h）随预报时效变化（a、e）10 dBZ，（b、f）20 dBZ，（c、g）30 dBZ，（d、h）40 dBZFig.9 The change of average POD（a，b，c，d）and MAE（e，f，g，h）of blending forecast for different thresholds with forecast time for four precipitation processes（a，e）10 dBZ，（b，f）20 dBZ，（c，g）30 dBZ，（d，h）40 dBZ

图10是4次降水过程不同尺度3种预报的平均POD 和MAE 随阈值变化。可以看出，0.01°× 0.01°尺度RFST 预报平均POD 随阈值增加明显减小，武汉RUC 模式预报和融合预报平均POD 随阈值增加变化不大，而其他尺度3 种预报的平均POD 随阈值增加呈先升后降趋势。不同尺度武汉RUC 模式预报的平均MAE 均最大，远高于其他2 种预报方法；0.01°× 0.01°尺度的融合预报和RFST 预报的平均MAE相差不大，其他尺度融合预报的平均MAE明显小于RFST预报，2种预报的平均MAE随阈值增加而减小，但融合预报的平均MAE 还随尺度增大而增大。另外，0.01°× 0.01°尺度的40 dBZ 阈值融合预报的平均POD（MAE）明显高于（低于）其他预报方法，其他尺度20 dBZ 阈值的平均POD 最大、MAE 最小，且融合预报平均POD（MAE）均高于（低于）其他2种预报。总体来看，融合预报明显优于单一预报。

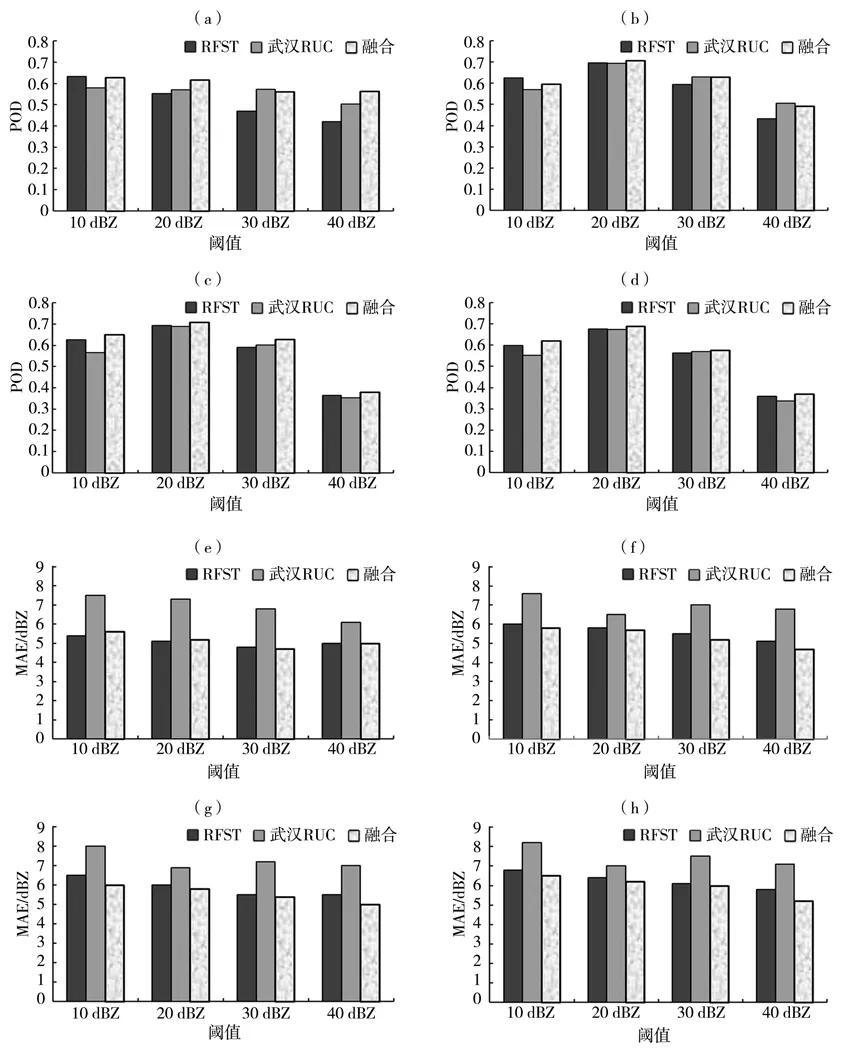
图10 4次降水过程不同尺度3种预报的平均POD（a、b、c、d）和MAE（e、f、g、h）随阈值变化（a、e）0.01°×0.01°，（b、f）0.02°×0.02°，（c、g）0.04°×0.04°，（d、h）0.08°×0.08°Fig.10 The change of average POD（a，b，c，d）and MAE（e，f，g，f）by three forecasts for different scales with thresholds for four precipitation processes（a，e）0.01°×0.01°，（b，f）0.02°×0.02°，（c，g）0.04°×0.04°，（d，h）0.08°×0.08°

4 结论与展望

本文借鉴香港天文台RAPIDS 技术思路，基于傅里叶-梅林变换、多尺度光流法和威布尔分布，以雷达实况为基准，实现了数值模式预报的雷达回波位置和强度校正方法，并结合改进的变分光流法的雷达回波外推预报，通过双曲正切函数给出融合权重，对雷达回波外推预报和校正后的模式雷达回波预报进行融合，初步实现了0~3 h 雷达回波融合预报，最后对湖北省2020年6—7月4次降水个例进行降水回波融合预报试验及检验分析。总体上，融合预报效果优于单一预报，尤其在强降水回波预报中有明显优势，对对流预报有积极作用。形成以下主要结论：

（1）利用傅里叶-梅林变换对模式预报的雷达回波场整体旋转角度和位移偏差进行修正，并采用MOVA 方法校正局部区域位置误差（相位误差），能够使数值预报雷达回波雨带走向和小范围回波区得到合理修正。统计发现，模式预报的雷达回波和实况均满足威布尔分布，且二者的概率密度分布函数相同，通过威布尔分布能够对数值预报雷达回波强度进行合理调整。

（2）武汉RUC 模式0~3 h 的降水回波位置和范围预报明显劣于雷达外推预报和融合预报，对于弱回波雷达外推预报略显优势，而对于强回波融合预报优势明显；POD 随回波阈值和预报时效增加而降低，而MAE 随回波阈值和预报时效变化不大，误差波动范围在2 dBZ以内。

融合预报效果主要依赖外推预报与数值模式预报，在2 种预报效果都正常的前提下融合预报效果优于单一预报，对0~3 h 定量降水预报有业务参考价值，但还存在诸多需要改进的地方：（1）利用双偏振雷达观测量改进现有的定量降水估计算法及改进雷达资料同化方法来提升数值模式对对流尺度降水的预报能力；（2）增加基于“对象”的检验分析方法，以便更好区分预报误差来源，从而给出预报降水场的整体属性；（3）改进融合预报方法，延长融合预报时效，进一步缩短匹配时间，从而使算法能够应用于实时性更高的业务中。