循环加卸载下高脆性黑砂岩强度及损伤试验研究

陈 珺，陈 念 辉，侯 靖

(中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122)

0 引 言

近年来，中国西部高山峡谷地区已建或正在兴建多个世界级的水电水利工程，建造了众多深部长大水工隧洞和地下洞室群。由于深部岩体常处于三向应力状态，洞室开挖卸荷引起围岩应力状态改变，围岩从三维应力状态向二维应力状态转变，在应力调整过程中，岩体内部裂隙不断萌生、扩展，损伤程度不断加深，进而影响了岩体宏观力学行为和破裂特征。同时，大量现场监测和室内力学试验表明，高应力下岩石常常表现出非线性特征[1]，这种非线性特征也反映了岩石在不同应力状态下或损伤破坏过程中其变形参数、强度参数不断劣化的过程。

针对硬岩变形破裂期间其力学行为与损伤的演化关系，许多学者开展了大量的试验和数值模拟研究。郑华康等[2]开展了大理岩三轴压缩力学试验，从细观角度探讨了岩石力学特性成因，并建立了可描述大理岩全应力-应变过程的黏聚力弱化-摩擦角强度改变模型。周洪飞等[3]提出了一种考虑弹性模量劣化的CWFS改进本构模型，并利用FLAC进行二次开发，实现了单轴压缩下岩石破裂过程和能量释放的细观模拟。王浪等[4]采用偏光显微镜研究了循环荷载下破坏岩体的微裂隙发展规律。倪卫达等[5]通过建立柱状节理岩体径向应力比与力学劣化系数的数学关系，得到了柱状节理岩体卸荷损伤效应的定量表达式。高春玉等[6]通过三轴加卸载试验，对大理岩在多个加载和卸载路径条件下的变形与强度变化规律进行了对比分析。众多研究表明，不同类型岩石在破坏过程中，其力学参数随其变形历史的演化规律差异较大，从试验角度进一步研究和揭示此演化规律，对构建可准确量化硬岩力学性质的力学模型具有重要意义。

为此，基于深部硬岩力学性质研究的需要，本文通过对黑砂岩开展循环加卸载试验，结合常规三轴试验结果着重分析岩石力学性质与破裂特征，研究岩石变形演化过程中力学参数随不可逆变形或损伤的演化规律，为后续开展围岩稳定性分析和安全性评价提供研究基础。

1 试验准备与方案设计

1.1 试样制备与设备

试验所用黑砂岩主要成分为石英、方解石和斜绿泥石，试样为标准圆柱体试样(Ø50 mm100 mm)，试样均从同一岩体中钻取，再采用磨石机将试样上下表面打磨光滑。根据规范要求，圆柱体试样两端平整度应控制在0.02 mm以内，两端平面与试样轴线垂直度不得偏离0.01 rad。试样在制备、运输和储存过程中应避免产生扰动和损伤。

本次循环加卸载试验在中科院武汉岩土力学研究所的岩石三轴实验系统(MTS815.03)上开展。该试验设备配有伺服控制的全自动三轴加载和测量系统，可进行岩土材料的单轴、三轴全过程试验，试验系统轴向最大出力为4 600 kN，最大围压为140 MPa，框架整体刚度为1.1×107kN/m，设备性能可满足本次试验要求。试验设备整体结构如图1所示。

图1 岩石三轴试验系统Fig.1 Rock triaxial test system

1.2 试验方案设计

为了解硬岩力学参数随损伤的发展演变过程，本次循环加卸载试验采用峰前峰后全过程围压保持不变、轴向应力加卸载的方式。开展试验前，需提前测定黑砂岩在各围压下的峰值强度，进而确定峰前峰后轴向应力卸载水平。试验共设置4个围压水平(10，20，30，40 MPa)。试验过程中首先将围压加载到预定值，再施加轴向荷载，达到预设的卸载强度值(峰值强度的50%，60%，70%，80%，90%和100%)后开始卸载。轴向荷载控制方式在峰前峰后加卸载阶段均采用轴向位移控制，加卸载速率为0.000 1 mm/s。为防止轴向应力卸载至零时导致压头与试样脱离，卸载期间将试样轴向应力卸载目标值设定为开始卸载时轴向应力的98%，一般约为1～5 MPa。

1.3 黑砂岩基本力学特性

经试验测试，黑砂岩试样单轴抗压强度达93.64 MPa，抗拉强度1.21 MPa，压拉强度比为77.39，属于典型的高脆性硬岩。为进一步了解黑砂岩力学特性，先后开展了不同围压水平下的三轴压缩试验，试验结果如图2所示，图中εa为轴向应变，εc为径向应变。具体来讲，在单轴压缩试验中，黑砂岩峰前基本呈线弹性变形状态，偏应力σ仅在峰值处出现少许波动，随后迅速跌落至零。对应的径向应变εc在峰值附近先保持缓慢增长，之后再大幅增大直到试样完全破裂。

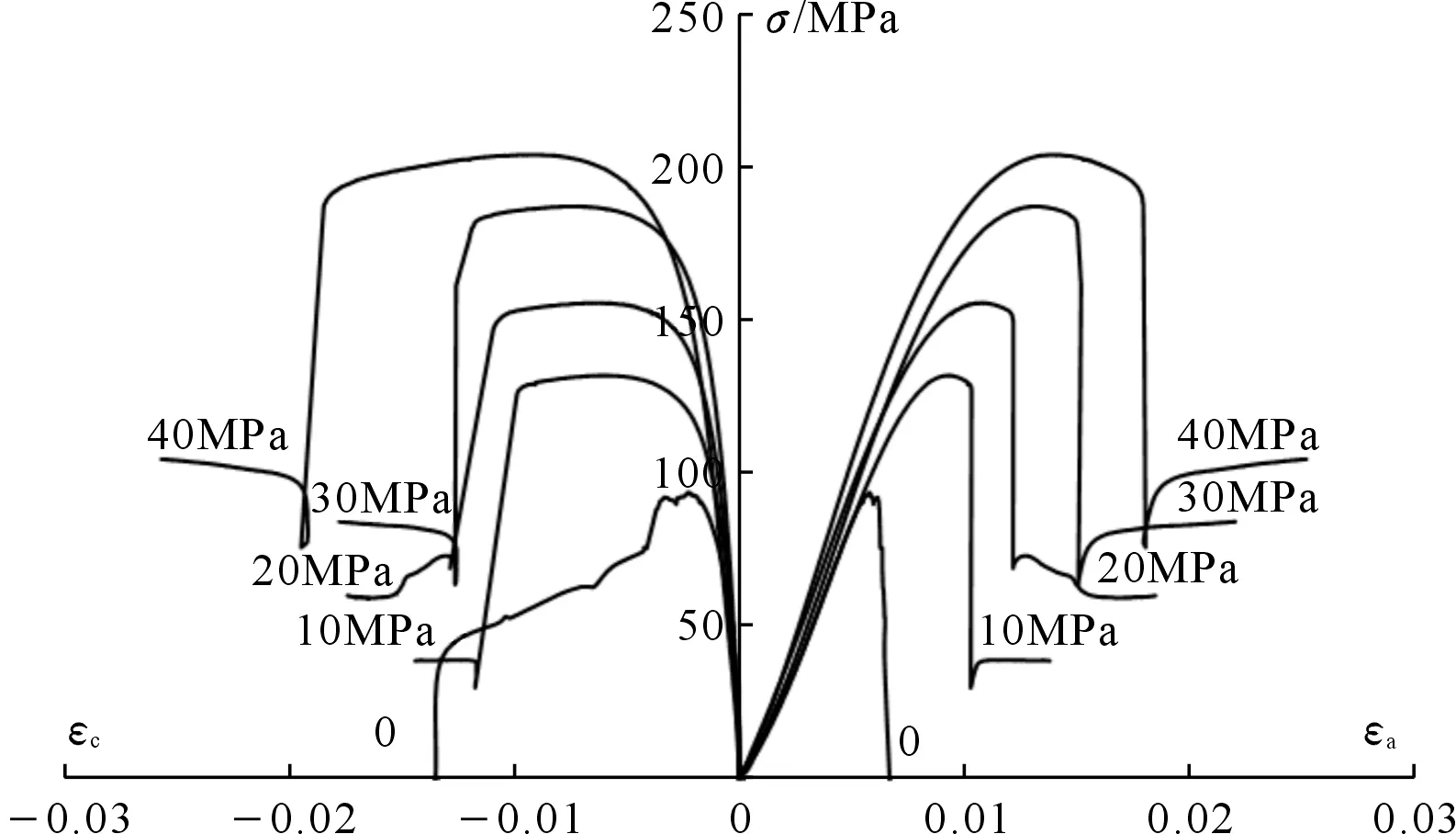
图2 黑砂岩三轴压缩试验应力应变曲线Fig.2 The stress-strain curves of black sandstone under triaxial compression tests

不同围压条件下黑砂岩应力应变曲线呈现出相同特性，均存在一定程度的屈服平台。所谓屈服平台是指岩石进入屈服状态，应力保持稳定或缓慢变化，而应变不断增加的特征。从图2中可以看出，随着围压的增大，屈服平台也逐渐增大，峰后发生应力跌落所对应的应变大幅增加。屈服平台的出现意味着岩石脆性的减弱，即黑砂岩的脆性程度随围压的增大而逐渐减小。但黑砂岩在10～40 MPa围压下，其应力应变曲线有一显著特征，即试样进入屈服状态一段时间后，应力会突然出现大幅度跌落，对应的侧向应变也出现了类似的变化特征。各围压下峰后应力跌落大小分别为102.14，86.83，123.70，128.41 MPa，应力降占峰值强度的比值分别为77.46%，55.77%，66.08%，62.93%，即峰后应力降程度随围压的增大趋向于减小。该特征反映出黑砂岩在围压条件下仍具有一定的脆性，在岩石进入屈服状态后，内部裂隙不断发育、扩张，损伤加剧，但未形成宏观破裂面；当内部裂隙相互连接、贯通，试样发生完全破坏时，应力则出现大幅跌落。

2 循环加卸载试验结果分析

2.1 应力应变曲线

图3为黑砂岩在4种围压水平下的循环加卸载试验应力应变曲线。从峰前峰后曲线总体特征来看，黑砂岩的应力应变曲线变化规律与常规三轴试验较为类似。岩石在加载阶段均出现线弹性变形和屈服变形，且屈服平台随着围压的增大而更加显著。在岩石发生破坏后，应力迅速跌落，由于试验中破坏往往在瞬间完成，此时难以控制应力卸载，造成每个围压下试样都出现一定程度的应力突降，这种峰后破坏特征与常规三轴试验破坏现象类似。

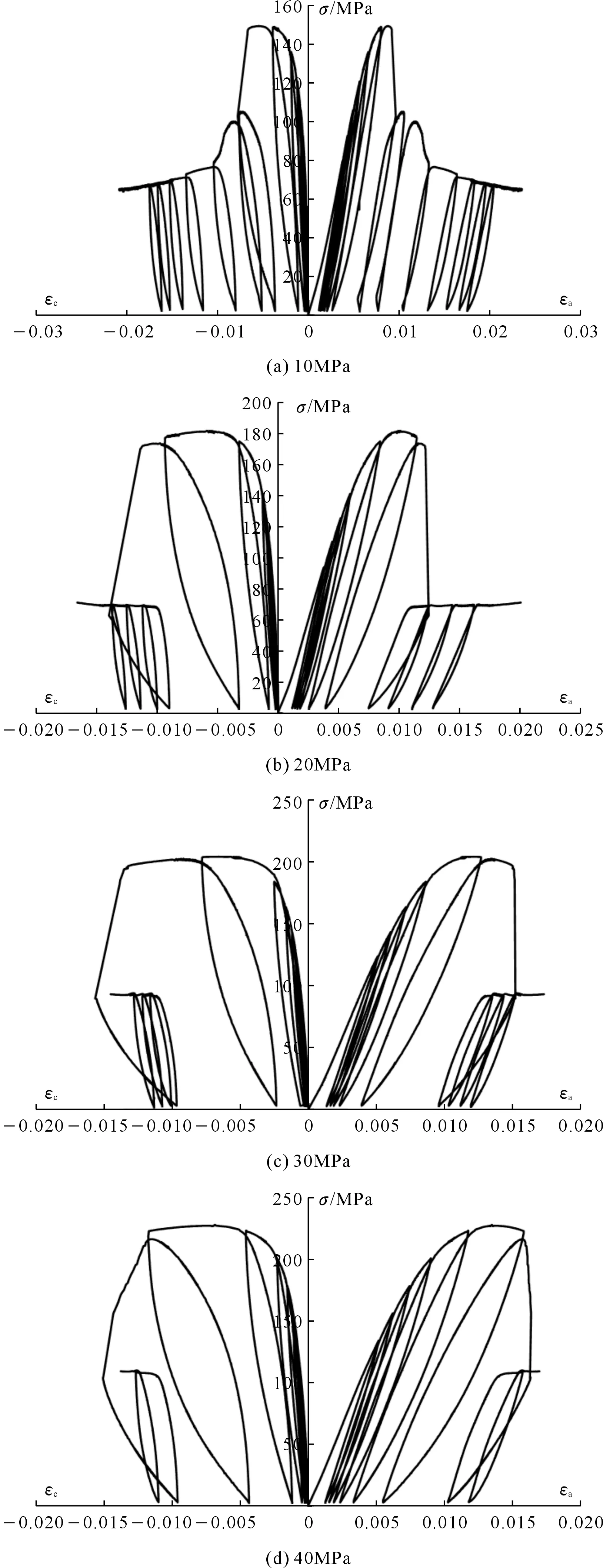
图3 黑砂岩循环加卸载试验应力应变曲线Fig.3 The stress-strain curves of black sandstone under cyclic loading and unloading tests

在10 MPa围压下，试样经过短暂的屈服变形后发生破坏，在应力跌落过程中切换控制模式，开始卸载轴向应力，完成4个应力循环后应力基本达到残余强度。对于20，30，40 MPa围压，试样到达峰值强度后，应力开始缓慢下降，此时卸载过程中试样均未破坏，表明岩石破裂面未完全形成。但在下一个循环中变形积累到一定程度，试样形成完整破裂面，出现应力跌落现象，应力基本直接降低到残余强度大小，随后的几个循环中应力最大值也在残余强度附近上下浮动。表1统计了黑砂岩各个围压下的峰值强度和残余强度，与常规三轴试验对比可知，循环加卸载试验中黑砂岩在10，20，30，40 MPa围压下峰值强度分别提高了13.3%，16.8%，9.1%和11.7%，平均为12.73%，残余强度则提高了118.2%，3.2%，46.5%和44.4%，平均为53.08%。

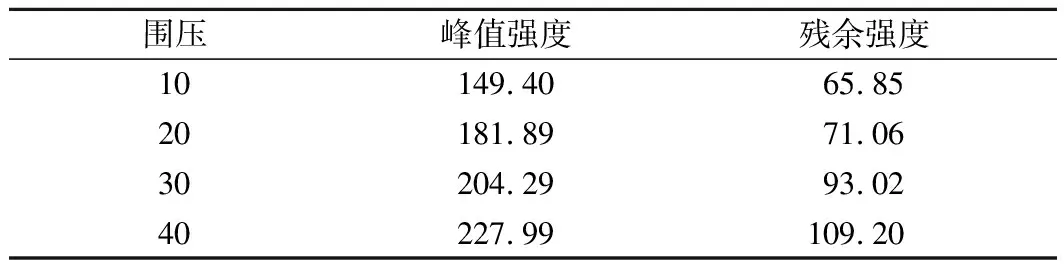
表1 黑砂岩在循环加卸载试验中的峰值强度和残余强度Tab.1 Peak strength and residual strength of black sandstone under cyclic loading and unloading tests MPa

2.2 变形破裂分析

根据图4黑砂岩加卸载试验后变形破裂形态可以看出，试样基本以剪切破坏为主。围压为10 MPa时主破裂面从试样顶部一直贯穿至试样底部，多条微翼裂纹伴随着主破裂面萌生、发展。同时，试样左侧出现一条水平向翼裂纹连通主破裂面，中部发育一条竖向张拉裂纹。水平向裂纹产生的原因可能是在加载过程中破裂面两侧相互错动，造成薄弱一侧挤压断裂，并萌生出竖向张拉裂纹。随着围压的增大，剪切破裂角逐渐增大，30 MPa围压时试样破裂面从中部开始发育，贯穿至试样底部。而40 MPa围压破裂面则为弧形，从试样中上部开始破裂，延伸到试样底部。掰开各试样破裂面，均可观察到表面存在大量岩粉，剪切破坏现象显著。

图4 黑砂岩在循环加卸载试验中变形破裂特征Fig.4 Deformation and fracture characteristics of black sandstone under cyclic loading and unloading tests

3 力学参数演化规律

在实际工程中岩石的破坏并不是立刻发生的，而是随着开挖的进行，应力不断调整，岩石内部微裂纹发育、扩展，损伤不断加剧，在超过岩石所能承受的极限应力状态后才发生破坏。这个过程中岩石会产生不可逆的塑性变形，其基本力学参数(如变形参数、强度参数)会随着塑性变形的增加而发生变化。因此，研究岩石从初始屈服到发生破坏再到残余变形整个过程中力学参数的演化规律对深刻认识岩石破裂机制具有重要的意义。

3.1 塑性内变量的确定

为了表征岩石的塑性变形程度，本文根据张凯[7]的研究成果引入塑性内变量这一参数来表征硬岩塑性程度。由于岩土材料在围压条件下往往发生剪切屈服，因此可取等效塑性剪应变为内变量κ[8]，通过公式(1)来计算获得考虑围压效应的等效塑性剪应变[7]。

(1)

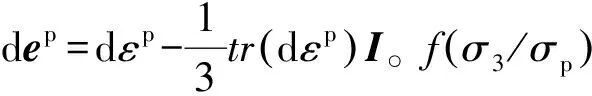
(2)

式中：参数A1，A2为待定系数，通过对试验数据拟合得到。

根据式(1)中塑性内变量κ的计算方法，当岩石处于初始屈服状态时内变量为0，当岩石处于残余变形时内变量为1。因此，在处理循环加卸载试验数据时应先确定各围压下岩石的初始屈服点，并计算对应的塑性剪应变。由常规三轴试验得到的应力应变曲线可知，岩石在达到峰值强度前，其体应变往往会发生转变，经统计体应变拐点对应的偏应力一般为峰值强度的80%。杨凡杰[9]研究成果表明，在体应变拐点之前卸载时，卸载点处的轴向应变对应的加、卸载应力基本相等；而在体应变拐点之后卸载时，对应的加、卸载应力相差较大，这说明当岩石所受应力超过体应变拐点对应的应力大小后，岩石内部微裂纹开始随着应力的增长而快速发育、扩展，即岩石的塑性变形开始逐渐增大。因此，可以把体应变的拐点作为初始屈服点，其对应的应力即为初始屈服应力。

通过该方法，本文计算了黑砂岩循环加卸载试验中4种围压水平下初始屈服点对应的等效塑性剪应变，建立起岩石从初始屈服到残余变形对应的等效塑性剪应变增量与围压之间的关系(见图5)，得到了围压函数f(σ3/σp)的具体形式(见公式3)，其中岩石的单轴压缩强度σp取93.64 MPa。根据拟合结果可以看出，随着围压的增大，黑砂岩从初始屈服到残余强度所经历的塑性变形增量也逐渐增大。

f(σ3/σp)=0.0106(σ3/σp)+0.0119

(3)

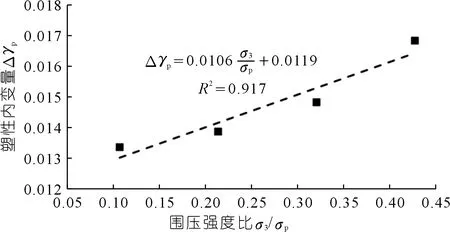
图5 黑砂岩等效塑性剪应变增量与围压的关系Fig.5 The relationship between equivalent plastic shear strain increment and confining pressure of black sandstone

3.2 变形参数随内变量的演化规律

岩石的变形参数包括弹性模量E和泊松比ν。深部地下岩体开挖过程中，随着围岩应力的重分布，表层围岩产生大量的微裂纹，在切向应力和施工扰动的作用下微裂纹进一步扩展、开裂，引起围岩力学性质劣化。如现场声波测试结果显示，表层围岩的波速是不断变化的，达到一定深度范围后才恢复至原岩波速水平[10-11]。此外，大量岩石力学试验结果也表明，岩石的弹性模量会随着岩石塑性变形的增加而逐渐减小[12-13]。

对于黑砂岩试样，在计算变形参数时将循环加卸载试验中每一次应力循环路径看作是一次单独的试验过程，分别将从卸载起点到卸载终点直线段的斜率作为岩石弹性模量，并根据对应的轴向应变来计算每次循环的泊松比，从而得到不同塑性程度下岩石的变形参数。考虑到不同围压下循环加卸载试验的每次应力路径中，岩石所产生的塑性变形量值各不相同，为便于总结参数演化规律，将塑性内变量在0～1范围内均匀等分化处理，按照线性插值方法计算出同一塑性内变量对应的岩石变形参数，进而获得了各个围压下变形参数随塑性内变量的演化规律，试验结果如图6所示。

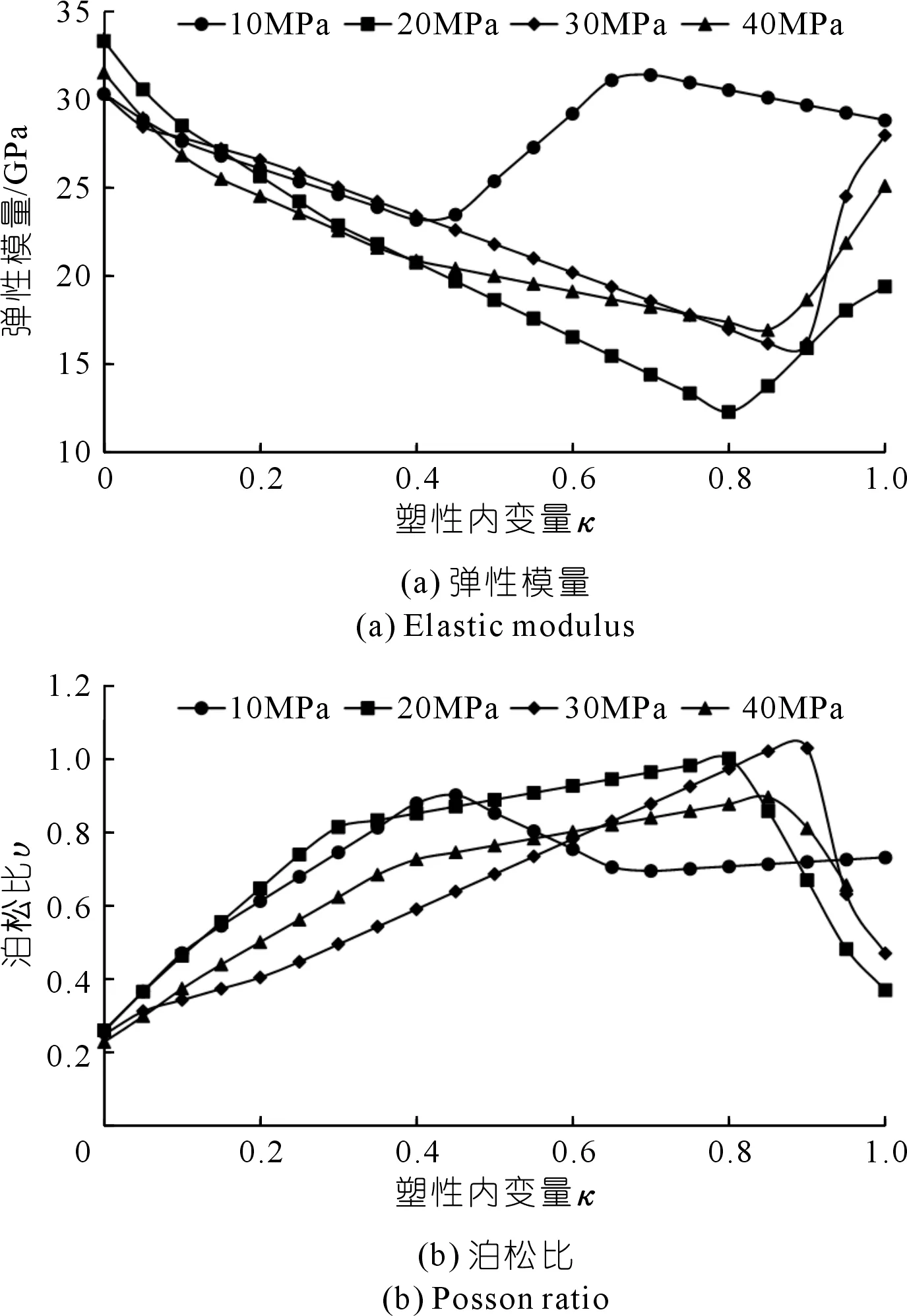
图6 黑砂岩变形参数随塑性内变量的演化规律Fig.6 The evolution of deformation parameters of black sandstone with plastic internal variable

根据计算结果，不同围压下黑砂岩从初始屈服到残余变形的过程中，其弹性模量、泊松比随塑性内变量的变化规律基本相同。弹性模量从初始屈服时便开始逐渐减小，在塑性内变量为0.80～0.85左右达到最小值，之后再快速增大。泊松比则从初始屈服时开始不断增大，并在塑性内变量为0.80～0.85左右时达到最大值，之后便快速减小。值得注意的是，4种围压下黑砂岩的泊松比在变化过程中均超过了0.5，甚至接近1，这对岩石材料来说是不可能的。泊松比即横向应变与轴向应变绝对值的比值，较大的泊松比表明岩石发生了较大的横向应变。结合岩石应力应变曲线发现，塑性内变量为0.85左右对应的应变均处于岩石发生应力跌落后的第一个卸载循环中，即岩石发生破坏后计算的泊松比达到最大值。由此可知，岩石在塑性变形过程中，内部微裂纹逐渐扩展、贯通，损伤不断加剧，发生破坏后试样形成完整破裂面，造成岩石横向变形的突然增大。岩石破坏后随着卸载的进行，在围压作用下破裂面又紧密闭合，从而产生较大的横向应变，而对应的轴向应变在整个过程中变化幅度较小，故计算得到的泊松比相对较大。

3.3 强度参数随内变量的演化规律

岩石的强度参数包括黏聚力c和内摩擦角φ，其计算方法类似于变形参数。首先，从体应变拐点对应的初始屈服点开始，针对不同围压下的循环加卸载试验结果，将每一次应力循环路径作为一次独立的试验过程，进而获得本次试验过程卸载时的大主应力，并计算卸载终点对应的塑性内变量。然后将塑性内变量均匀等分化，分别对不同围压下黑砂岩的大主应力进行线性插值处理，得到各个塑性内变量对应的大主应力，进而获得了不同塑性内变量下黑砂岩大、小主应力的关系。最后，通过线性函数拟合大、小主应力数据，并根据线性莫尔-库伦准则计算得到不同塑性内变量对应的黏聚力c和内摩擦角φ，从而建立黑砂岩的强度参数与塑性内变量κ之间的函数关系，计算结果如图7所示。

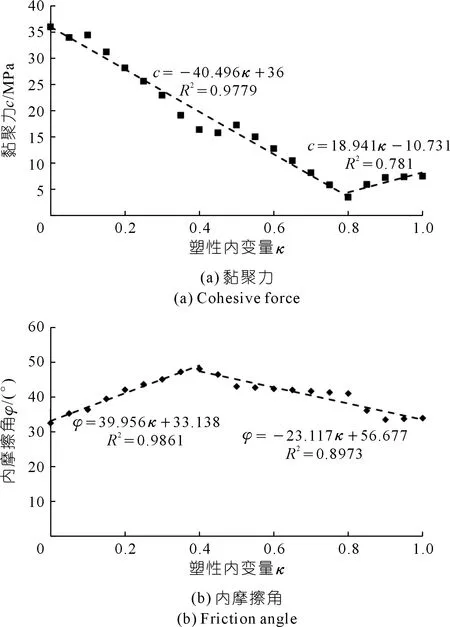
图7 黑砂岩强度参数随塑性内变量的演化规律Fig.7 The evolution of strength parameters of black sandstone with plastic internal variable

根据图7中黑砂岩强度参数的变化特征，黏聚力在塑性内变量增大过程中呈现出先小幅增大，再快速降低，最后趋于稳定的变化趋势，内摩擦角则呈先逐渐增大后缓慢降低趋势。对于黑砂岩黏聚力的这种变化特征，可解释为在整个加载过程中，随着岩石塑性变形的增大，岩石内部损伤逐渐增多，由于微裂纹不断发育、扩展，造成岩石微观结构不断分离，岩石颗粒之间黏结强度不断降低，宏观上表现出黏聚力随塑性内变量增大而出现减小的趋势。在初始损伤阶段(κ<0.1)，黏聚力有一段小幅增大的过程，根据塑性内变量的定义，κ=0对应的是岩石的初始屈服点，即体积应变拐点的应力，并非峰值强度点，在此阶段岩样的内部微裂纹逐步扩展，但细观结构的破坏尚不能降低岩石的承载能力，因此，岩石的黏聚力在初始屈服阶段表现出增大的趋势。此外，当塑性内变量达到0.8左右时，岩石完全破坏形成贯通的完整破裂面，造成岩石颗粒之间基本丧失黏结强度，故黏聚力减小至最小值，之后在应力接近残余强度过程中趋于稳定。

而微裂纹的发育和细观结构的分离，促使潜在破裂面表面更加粗糙，造成岩石颗粒之间的摩阻力增强，宏观上表现为内摩擦角的增大。当塑性内变量达到0.4左右时，岩石内摩擦角达到最大值，之后便出现阶段性减小现象。这种情况主要是由于岩石粗糙的破裂面在尚未完全贯通时形成了互锁结构[14]，使计算得到的摩擦系数大于岩石破裂面自身的摩擦系数。当岩石沿微裂纹滑移时，互锁结构逐渐开始破坏，计算得到的摩擦系数减小至岩石破裂面的摩擦系数，从而造成内摩擦角出现逐渐下降的现象。

根据上述计算结果，对强度参数的演化规律进行数据拟合，得到了黑砂岩黏聚力、内摩擦角与塑性内变量的关系方程。由于岩石黏聚力先随塑性内变量不断减小，并在接近残余强度时保持稳定的变化规律，而内摩擦角则呈现出先增大后减小的变化特征。因此，黑砂岩的强度参数与塑性内变量之间的关系方程宜采用分段函数来表示，拟合结果见图7，分段函数如公式(4)和(5)所示。

(4)

(5)

根据拟合结果，黑砂岩的强度参数与塑性内变量可以采用线性分段函数进行描述。随着塑性变形的增大，岩石的黏聚力逐渐减小，在塑性内变量为0.8时比起初始屈服值减小了90.3%。内摩擦角则先增大后减小，在塑性内变量为0.4时比起初始屈服值增大了47.9%。

4 结 论

为研究脆性硬岩变形破裂过程中力学特性随损伤的演变规律，本文利用高脆性黑砂岩开展了不同围压水平的循环加卸载试验，获得了黑砂岩在循环加卸载应力路径下的强度与变形特征，并以塑性内变量作为表征岩石损伤程度的指标，研究了黑砂岩从初始屈服到发生破坏再到残余变形整个过程中力学参数的演化规律，主要研究成果如下。

(1) 循环加卸载试验中黑砂岩的力学特性与变形破裂特征与常规三轴试验结果较为类似，试样峰值强度比常规三轴试验提高了12.725%，在峰后阶段均出现一定程度的应力跌落，形成完整剪切破裂面。

(2) 岩石变形参数在不同围压下具有相同的变化规律，其弹性模量随塑性内变量呈先减小后增大的变化趋势，而泊松比则呈现增大后减小的趋势。

(3) 对于岩石的强度参数，其黏聚力在塑性内变量增大过程中呈先小幅增大，再快速降低，最后趋于稳定的变化过程，内摩擦角则呈先逐渐增大后缓慢降低的趋势。对于强度参数的演化规律，可采用线性分段函数来描述岩石黏聚力、内摩擦角与塑性内变量的关系。