某火炮取弹装置故障仿真分析

李志刚,羊 柳,尹 强,赵 飞,王 健

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国人民解放军63850部队,吉林 白城 137001)

随着科学技术的飞速发展,军事战场日趋现代化,对中大口径火炮系统的发射速度也有了更高的要求。自动装填技术不同于以往的人工装填,可以在很大程度上实现火炮自动化,是提高火炮射速的关键技术之一。供弹系统是自动装填系统的一部分,在自动装填系统中发挥至关重要的作用。供弹系统在装填过程中,取弹装置会受到碰撞冲击,还会存在驱动齿轮故障等状况。提高弹丸取送过程的速度和稳定性对于火炮提升射速至关重要。因此,分析取弹装置取弹送弹过程的动态特性具有重要的实际意义。

本文采用动力学仿真软件和控制仿真软件建立取弹装置联合仿真系统模型,并对该模型进行动态分析。选取驱动齿轮的磨损故障和滚动轴承的疲劳脱落故障,分析驱动齿轮的不同磨损状态和滚动轴承的疲劳脱落状态对取弹装置伸缩过程速度和到位精度的影响。该方法可为供弹系统磨损机理和故障诊断方面的研究提供一定的参考。

1 取弹装置的工作原理

取弹装置的结构主要包括:主体、抱爪、滑板、齿条、限位块、底板、座圈和伸缩电机等,如图1所示。

图1 取弹装置结构图

取弹装置的工作原理:伸缩电机输出端连接减速器,减速器与驱动齿轮同轴连接。当取弹装置开始送弹取弹工作时,系统对伸缩电机发出指令,伸缩电机为驱动齿轮提供驱动力矩,驱动齿轮与齿条啮合,齿条与滑板固定,故驱动齿轮转动会带动整个取弹装置工作,驱动齿轮与编码器同轴相连接,滑板的实时位移会被编码器检测到并反馈给控制系统,从而确保取弹装置伸缩动作的位置精度。

2 联合仿真模型建立

2.1 动力学模型的建立

根据取弹装置各部分结构的相对位置以及装配关系,在建模软件中建立其三维模型,然后将三维模型保存为x_t文件格式,并导入到动力学仿真软件中,达到模型的精准建立。本文主要针对取弹装置的伸缩运动进行研究,故在建模过程中,将不存在相对运动的结构进行布尔加计算或添加固定副。对存在相对运动的结构,依据其运动关系添加旋转副、滑动副并设置接触,将相关参数修改为实际值。最终模型如图2所示。在三维建模软件中分析取弹装置各结构的质量属性,并在动力学仿真软件中输入其质量、转动惯量和质心位置,从而确保得到精确的取弹装置仿真模型。模型各部件拓扑关系为主体和滑板之间通过固定副连接,座圈与大地为固定副连接,驱动齿轮轮与大地为转动副连接。

图2 动力学模型

2.2 联合仿真系统搭建

选用控制仿真软件建立取弹装置模型,联合仿真系统由两部分搭建,一部分是从控制仿真软件中导出的机械子系统模块,另一部分是软件中的控制模块。采用如图3所示的PID控制算法对驱动齿轮进行控制。以取弹装置理想位移曲线与仿真得到的实际位移曲线的误差作为控制量,实时调整驱动齿轮端的输入力矩。

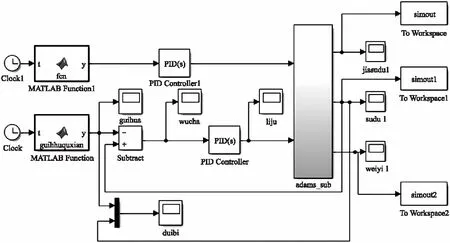
图3 联合仿真系统模型

3 仿真与试验验证

为保证取弹装置模型的正确性和精度,本文采用实验数据与仿真结果对比校核的方法来验证仿真模型。在某自动装填系统实验台架上采得取弹装置滑板伸缩位移、伸缩速度等数据。

由于取弹装置伸缩过程会根据负载的不同设置不同的时序要求,所以试验测试分为两种工况。第一种是带弹伸缩,即在控制系统中发送1 s的时序指令;第二种是空载伸缩,即在控制系统发送0.6 s的时序指令。

仿真实验中设置与实验相同的指令,采集联合仿真模型输出的两种工况下的伸缩位移和伸缩速度。模型输出曲线与实测曲线分工况进行对比,结果如图4～图7所示。

图4 带弹位移曲线图

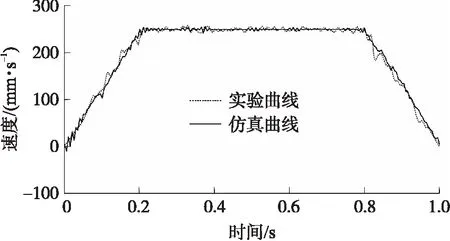
图5 带弹速度曲线图

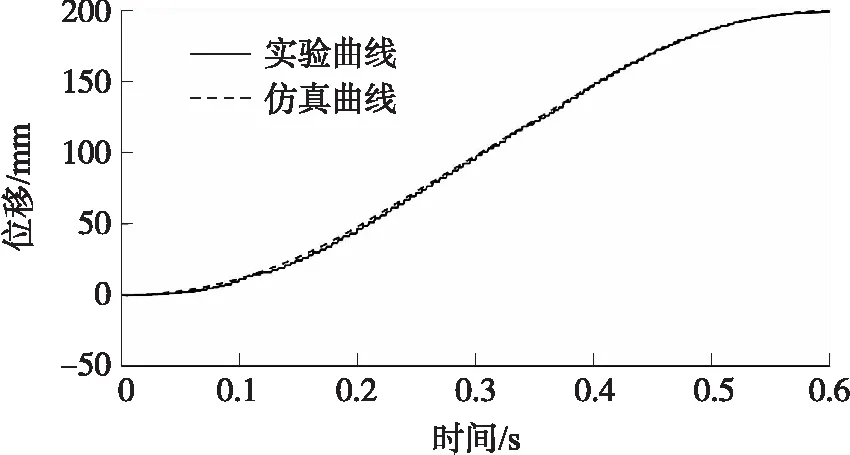
图6 空载位移曲线图

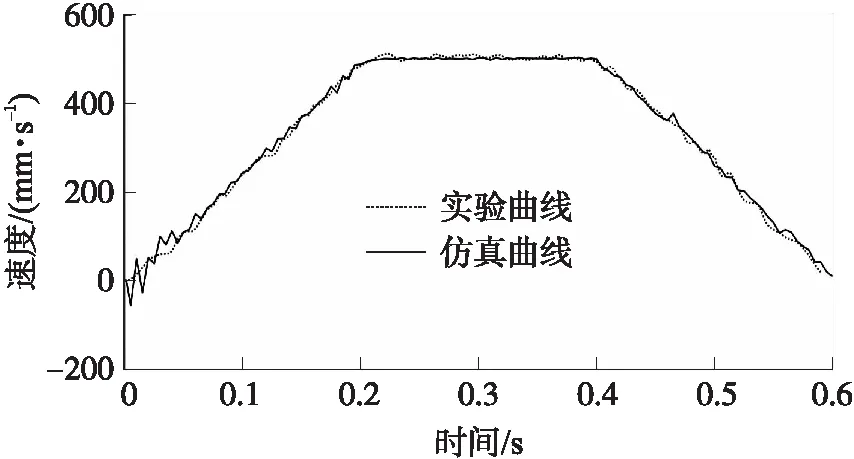
图7 空载速度曲线图

表1为实测与仿真的对比结果。从最大误差、平均误差及标准差的值可看出仿真结果与实测结果是十分接近,模型具有较高的可信度。

表1 实测数据与仿真结果对比

4 故障仿真分析

自动装填系统作为一个复杂的机电集成系统,工作过程中会出现各类故障类型,并且由于各种因素的耦合,还会形成各类故障现象。通过分析常见的故障机理以及故障统计,本文选取驱动齿轮磨损和轴承疲劳脱落这两个典型故障,对取弹装置伸缩过程进行故障分析。

4.1 齿轮磨损计算模型

齿轮啮合位置的变化会导致啮合刚度发生变化。当轮齿齿条啮合时,啮合点处的啮合刚度可表示为

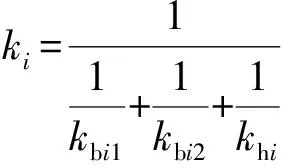
(1)

式中:1为齿轮;2为齿条;b为剪切与压缩变形后的刚度;h为Hertz接触变形后的刚度。其中齿轮刚度b具体表示为

(2)

将轮齿划分为个面积单位,每个面积单位都有矩形截面的短梁。式(2)中:为截面刚度系数;为齿轮泊松比;为面积单位短梁厚度;为横截面积;为微元面积到截面轴线距离乘积;为面积单位与啮合处的距离;为啮合处对应的压力角;为啮合处距轮齿中性层的距离。刚度h是一个常数,其表达式为

(3)

式中:为实际接触齿宽;,为两齿轮弹性模量;,为两齿轮泊松比。

齿轮均匀磨损导致面积单位的与发生改变,从而导致啮合刚度降低。假定为面积单位的磨损深度,当齿轮发生均匀磨损,′与′分别变为

′=-

(4)

′=-(-)

(5)

式中:为微元处齿面距轮齿中性层的距离。

4.2 齿轮磨损故障仿真

取弹装置的伸缩动力来源于电机驱动齿轮运转,从而带动和滑板固定的齿条移动,其装配关系如图8所示。在取弹装置进行伸缩动作的时候,驱动齿轮和固定在滑板上的齿条会反复啮合,啮合过程会产生不可避免的冲撞,造成啮合面磨损。当磨损量达到某种程度,就会间接影响传动效率和取弹装置的到位精度。而一旦因为磨损故障导致取弹装置的伸缩动作受到影响,就可能会产生取弹卡滞、送弹不到位等状况,从而影响供弹系统性能。

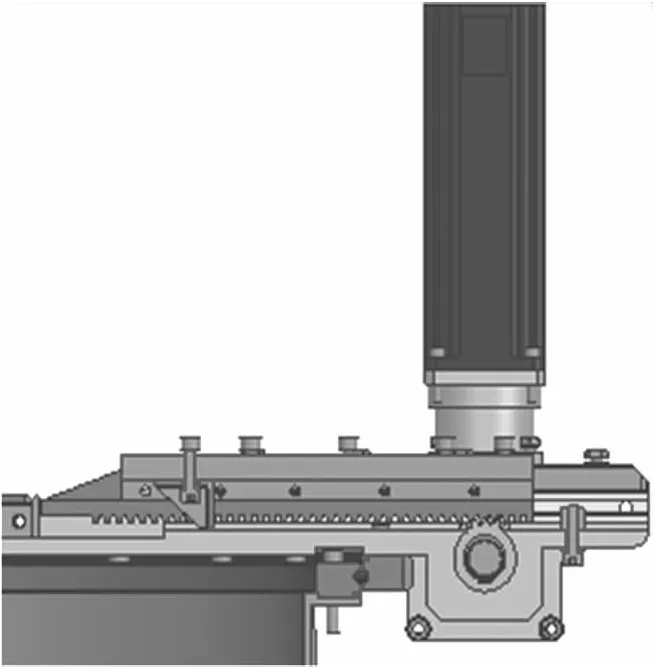
图8 齿轮齿条系统装配图

磨损是零部件失效的一种基本类型,通常是指零部件的几何尺寸(体积)变小。磨损会对机械性能造成影响,从而造成机械故障,使其无法达到正常工作状态。由于磨损是一个复杂的随机过程,并且齿轮齿条啮合时,齿条的每一个齿与驱动齿轮的齿只啮合一次,而驱动齿轮的每个齿轮啮合了很多次,所以磨损较快。故针对齿轮磨损故障研究时,假设驱动齿轮上出现均匀磨损情况,且齿条没有发生磨损。当驱动齿轮出现磨损时,其几何尺寸发生改变。

由于在实体齿轮上不便进行人为破坏,并且无法精准掌握磨损的程度。故以式(4)和式(5)为依据选择故障注入的方法在三维模型上以齿顶长度为标准对驱动齿轮的齿形进行均匀磨损处理,然后与齿条进行装配,以此模拟磨损故障。通过对比不同尺寸的故障注入,选取其中具有代表性的三组磨损状态,分别是磨损1/12、1/6和1/4。磨损齿轮齿条装配模型如图9所示。

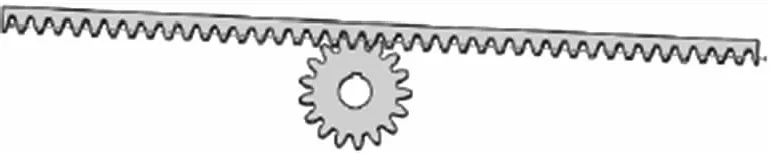
图9 磨损齿轮齿条装配简化模型

在驱动齿轮的三维仿真模型中注入不同磨损量,模拟其磨损故障。采用同样的控制策略进行联合仿真,并保持其他参数不变,获得在驱动齿轮不同磨损程度故障下取弹装置相关的运动特性,结果如图10和图11所示。

由图10可以看出,驱动齿轮磨损1/12时,取弹装置的位移曲线相较无磨损状态的位移曲线基本保持一致。驱动齿轮磨损1/6时,取弹装置的位移曲线相较无磨损状态的位移曲线从0.7 s时开始出现分离,直至到达194.2 mm最终位移,与规划位移相差6 mm。驱动齿轮磨损1/4时,取弹装置的位移曲线相较无磨损状态的位移曲线同样是从0.7 s时出现分离,直至达到162.4 mm最终位移,与规划位移相差37.6 mm。由此可以得出,驱动齿轮磨损的越严重,行驶位移相较规划位移相差得越大。

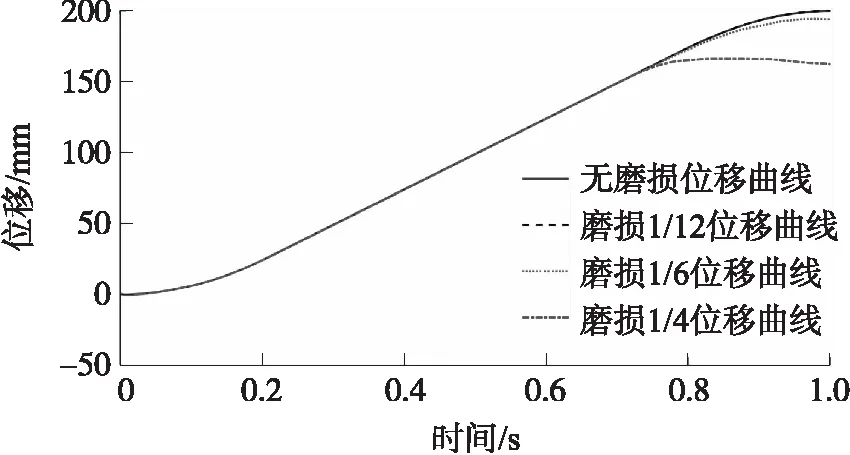
图10 驱动齿轮磨损后位移曲线对比图

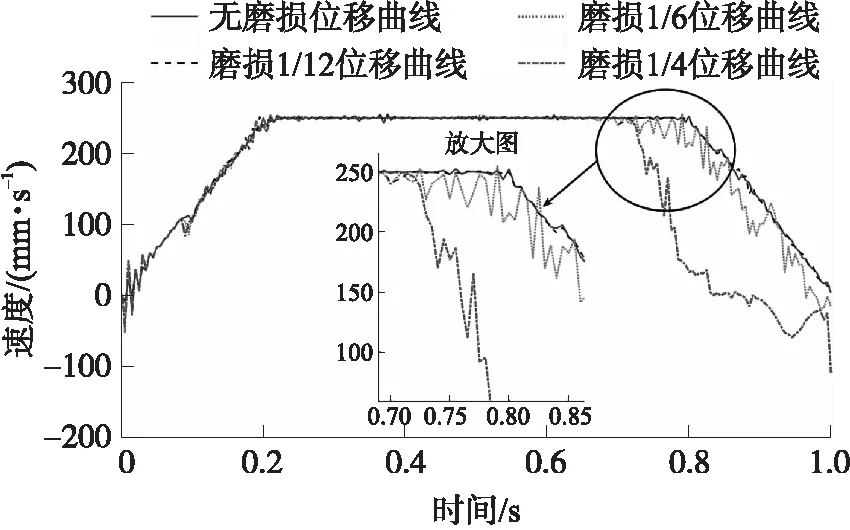
图11 驱动齿轮磨损后速度曲线对比图

由图11可以看出,驱动齿轮磨损1/12时,取弹装置的速度曲线相较无磨损状态的速度曲线基本保持一致,但是在0.7 s时速度会出现一些轻微的波动,在随后的运动中又按照规划速度曲线运动。驱动齿轮磨损1/6时,速度曲线相较无磨损状态的速度曲线出现了明显的变化,速度曲线从0.7 s时开始出现明显波动,并在0.885 s时,出现72.08 mm/s的最大速度差。驱动齿轮磨损1/4时,速度曲线相较无磨损状态的速度曲线变化最大,速度曲线从0.7 s时开始出现剧烈波动,并且在0.8 s时,出现219.8 mm/s的最大速度差。

综合图10和图11可以得出,取弹装置伸缩过程会在0.7 s出现波动。这是因为0.7 s时取弹装置伸出150 mm,此时取弹装置主体和弹丸重量过大导致伸出部分产生向下的倾斜,增大了齿条与驱动齿轮啮合处的压力。而当驱动齿轮无磨损的时候,由于啮合精度较高取弹装置可以按照预计状态行进;但当驱动齿轮磨损到一定程度后,伸出部分倾斜对啮合处产生的力导致驱动齿轮所需力矩增大,降低了取弹装置的伸出速度,进而脱离规划曲线。根据供弹系统结构交接5 mm的余量设计,即当取弹装置伸出距离小于195 mm时无法完成弹丸交接,故当驱动齿轮磨损1/6时,取弹装置被认定成故障状态。

4.3 轴承疲劳脱落故障仿真

滚动轴承是高精密度的机械元件,具有旋转精度高,承载能力强维护便捷的优点,被广泛应用于机械以及相关领域。滚动轴承减少摩擦副之间的摩擦磨损原理,是将运转工作轴和固定轴座二者之间的滑动摩擦变成滚动摩擦。通常情况下,在取弹装置结构中滚动轴承会被用于降低电机输出轴与驱动齿轮之间的摩擦,其装配关系如图12所示。在滚动轴承的旋转运动中,由于内圈接触面与滚动体之间会无法避免地产生弹性滑动,导致滚动体与轴承内圈二者的转速不统一,轴承的状态变为滚滑运动状态。当轴承的滚动体与内圈接触做滚滑运动时,受轴承润滑效果变差以及密封性不佳等诸多因素的影响,接触面产生轴承打滑,导致接触面间的摩擦因数在一定程度上增大。轴承打滑会加剧轴承内部构件间存在的摩擦磨损,导致运转轴承出现磨损,增加其产生剥落或疲劳点蚀等诸多类型疲劳磨损故障的可能性,致使机械无法正常使用。

图12 轴承系统装配图

滚动轴承作为机械的重要零件,同时也是传动系统易损件之一,据不完全统计,旋转机械故障约30%是因滚动轴承引起的。其中点蚀故障最为常见,即轴承上面出现小的坑洞,对于外径不超过60 mm的轴承来说,面积一般不大于2 mm×2 mm。点蚀是轴承不可避免的故障,也是轴承最常见的失效形式。

当点蚀面积扩大,滚道表面材料会出现成片的剥落,形成面积非常大的坑洞。此时,轴承故障处于后期,容易出现振动、卡死等现象,即轴承的疲劳脱落故障。疲劳剥落是滚动轴承中较为常见的故障类型,这种故障通常发生在滚动体表面和套圈滚道,具体现象为滚道的表面会出现不平整的鳞形状以及疲劳扩展的海滩状纹路,并且存在一定的深度和面积。当发生疲劳脱落故障时,滚动轴承会发生强烈的冲击振动,具体是以冲击点为原点,以球面的形式由内向外不断扩散,并且通过相应机构传入箱体以及机架。对轴承故障进行仿真,积累故障样本并研究其故障机理,可以尽早地识别其疲劳脱落故障,进而防止整个系统失效。

同样选择故障注入的方法在三维模型上对轴承滚动体表面进行尺寸修改,人为制造出疲劳剥落故障。仿真对象为FAG6004型轴承,其主要参数为:外圈直径42 mm,内圈直径20 mm,厚度12 mm。修改后的轴承三维图如图13所示。选取轴承滚动体表面剥落面积为3.5 mm×5 mm作为代表性故障进行运动特性分析,结果如图14和图15所示。

图13 轴承疲劳脱落三维图

图14 轴承疲劳脱落位移曲线对比图

图15 轴承疲劳脱落速度曲线对比图

由图14可以看出,当滚动轴承出现疲劳剥落时,取弹装置的位移曲线相较规划位移曲线基本一致,最终位移可以达到200 mm的预计位移。但是在0.1 s时,取弹装置的位移曲线开始偏离预定位移曲线,并且从0.2 s起曲线偏离的较为明显,0.8 s开始曲线逐渐回归预定位移曲线,经过0.9～1 s这段时间,疲劳剥落曲线相较预定位移曲线基本一致。最大位移差为5.3 mm,出现在0.6 s的时候。由此可以看出,轴承疲劳剥落故障对运动位移影响不明显。

由图15可以看出,当滚动轴承出现疲劳剥落的时候,取弹装置的速度曲线相较规划速度曲线出现了振荡波动。在0～0.1 s这段时间,取弹装置开始加速,疲劳剥落速度曲线在规划速度曲线周围出现轻微振动,最大速度差为20.3 mm/s,出现在0.08 s的时候;在0.1～0.2 s这段时间,取弹装置继续加速,疲劳剥落速度曲线振荡加剧,最大速度差为23.5 mm/s,出现在0.19 s的时候;在0.2～0.8 s这段时间,取弹装置速度达到最大,同时疲劳剥落速度曲线振动在这段时间也最为剧烈,最大速度差为25.6 mm/s,出现在0.65 s的时候;在0.8～0.9 s这段时间,取弹装置开始减速,疲劳剥落速度曲线振动相较匀速段有明显的降低,最大速度差为19.8 m/s;在0.9～1 s这段时间,取弹装置继续减速,疲劳剥落速度曲线振动降到最低状态,最大速度差为25.22 m/s。由此可以看出,滚动轴承发生疲劳剥落故障会导致速度出现波动,波动的频率随着速度的升高而升高。

5 结论

通过一体化仿真的方法,对取弹装置驱动齿轮磨损故障和滚动轴承疲劳剥落故障两种典型故障模式进行仿真研究。通过联合仿真,获得了两种故障模式分别发生的情况下取弹装置的动力学和运动学特性。根据仿真结果,验证两种故障模式都会导致取弹装置伸缩运动不平稳。具体结论为:

①驱动齿轮磨损后,受力发生明显的不均匀,从而导致整个取弹装置的运动状态变差、工作性能降低。从仿真过程和结果来看,驱动齿轮磨损时,取弹装置送弹动作会出现抖动情况,到位精度相较无磨损状态明显降低。随着磨损量加大,故障特性表现得更加明显。

②轴承发生疲劳剥落后,取弹装置整体到位精度未发现明显变化,但是运动过程发生剧烈的抖动,从而导致取弹装置运动过程速度状态无法保持稳定,并且随着运动时速度的加快抖动愈发剧烈。

综上,采用一体化仿真的方法,模拟仿真供弹系统中取弹装置所存在的故障,可以获得驱动齿轮磨损和滚动轴承疲劳剥落状态下的系统工作特性,对仿真结果进行分析研究,为以后取弹装置故障的预测和诊断提供可靠的理论依据,对取弹装置的日常维护工作有一定的参考价值。