高斯混合模型自适应盲信号分离

马 诚，李云红，陈锦妮

（西安工程大学 电子信息学院，陕西 西安 710048）

0 引 言

盲信号分离又称盲源分离，是现代信号处理领域的一个新热点。近20年来，盲信号分离问题得到了国内外学者的广泛关注，它是指不依赖任何有关混合矩阵的先验信息，从多个传感器观测到的混合信号中恢复未观测到的信号源。根据源信号经过传输信道的混合方式不同划分为三种：线性瞬时混合模型、线性卷积混合模型、非线性混合模型。截至目前，研究最多的是线性瞬时混合模型，本文提出的盲信号分离算法也是针对该模型。

独立分量分析（Independent Component Analysis，ICA）是在源信号服从非高斯分布的条件下，以各维信号之间的独立性作为其准则函数，并进行算法优化，分解成各个独立分量，完成信号的盲分离。Kernel ICA算法是在独立分量分析方法中引入核函数，将信号从低维空间映射到高维特征空间，然后对映射数据采用独立分量分析方法。该算法的分离效果较好，但是计算复杂度往往较高，难以满足实际在线的需要，并且该算法的鲁棒性较差。高斯混合模型是一种经典的语音信号模型，在语音识别、语音转换等领域被广泛应用。对此，本文提出基于高斯混合模型的自适应盲信号分离算法，该算法由于在线估计混合信号的评价函数，因而模型更为精确，分离效果较好，并且可以用于非平稳信号的分离，算法的实用性提高。高斯混合模型还可以逼近任意源的概率密度函数，提高算法的鲁棒性，使得盲信号分离效果较好。

1 高斯混合模型盲信号分离算法

1.1 盲分离算法的基本理论

假设=[,,…,x]为通过传感器接收到的观测信号，为传感器的个数；为×混合矩阵；源信号为个相互独立的未知信号。因此，线性瞬时信号的数学模型可表示为：

盲信号分离就是在只知混合信号的前提下，寻找分离矩阵，使得输出信号=尽可能逼近源信号。

1.2 概率密度估计理论

最小互信息盲信号分离算法的代价函数为：

由式（2）可知，只有当(y)=[ ln p(y)]时，才可以实现信号的准确分离。本文采用基于高斯核函数的概率密度函数估计理论，直接估计混合信号的评价函数。

假定y为混合信号，=1,2,…,，为信号的维数，样本个数为，其边缘概率密度函数可表示为：

式中：表示核函数窗宽；表示高斯核函数，即：

Y为：

式中表示混合信号的第个样本。对于一个给定的随机信号，上述基于高斯核函数的估计边缘概率密度函数等于真实的概率密度函数。为了求得概率密度函数的导数，上述概率密度函数的梯度形式如下：

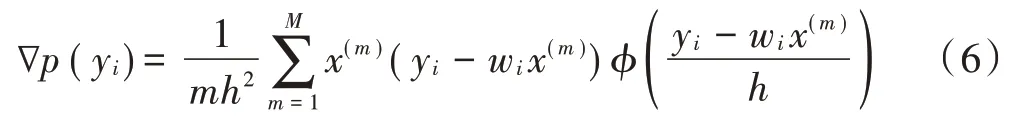
则对于给定的数据，其概率密度函数形式为：

1.3 优化函数求解

求解式（2）的评价函数，对于给定的数据集，则式（2）可写为：

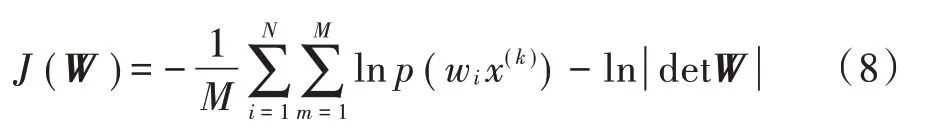
将式（8）第一项用-()代替，则式（8）可写为：

式（9）中()的形式如下：

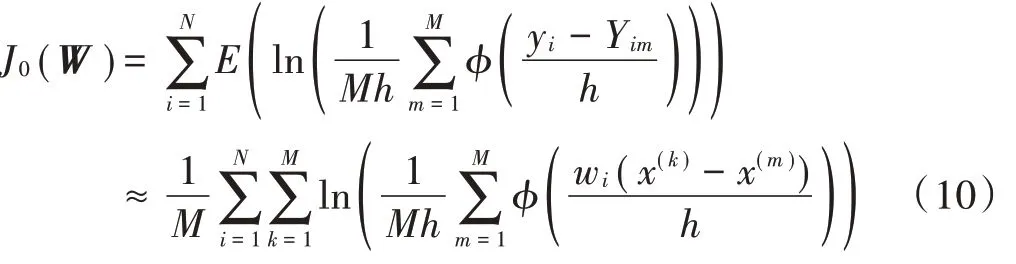
因此，盲信号分离问题就转化为式（11）所述的优化问题：

对于给定的信号,=1,2,…,，式（11）实质上是一个非线性优化问题，也可经过预白化处理，实现信号的零均值、单位方差处理，从而简化运算。

1.4 优化算法

式（11）实际上是关于分离矩阵的优化求解问题：

为了描述方便，定义下面的公式：

则式（12）中的∇()可以写为：

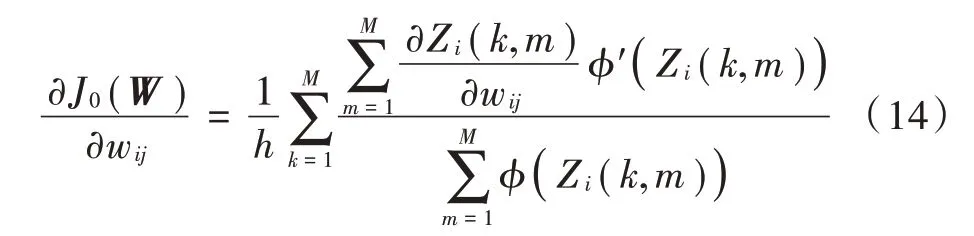
式中：

对优化函数式（11）中的约束条件做归一化处理，如下所示：

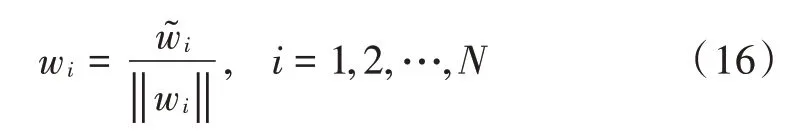
根据式（16），分离矩阵可以写为：

式中：

因此，优化函数式（11）中ln ||det可写为：

则式（19）对w的微分如下：

如果是正交矩阵，有：

根据上面的计算，则式（10）的微分形式为：

式中：

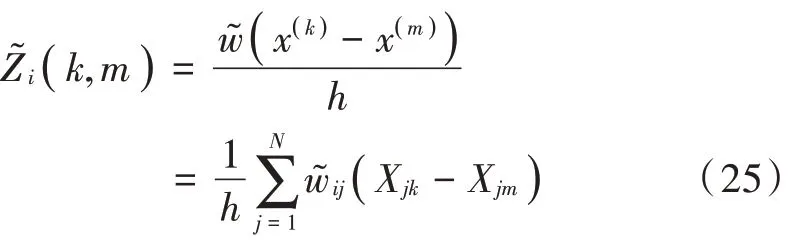
2 实验结果

为了验证本文算法的有效性，选取轻拖尾与轻拖尾、重拖尾与重拖尾、重拖尾与轻拖尾三组混合信号进行分离。

1）轻拖尾与轻拖尾混合信号的分离

图1代表源信号（横轴为采样点数，纵轴为幅度），4个源信号依次是正弦信号（周期为20 s）、锯齿波信号（周期为100 3 s）、高斯白噪声和正弦信号（周期为80 s），归一化峭度分别为：-1.301，-1.102，0和-1.926，采样点数为1 000。

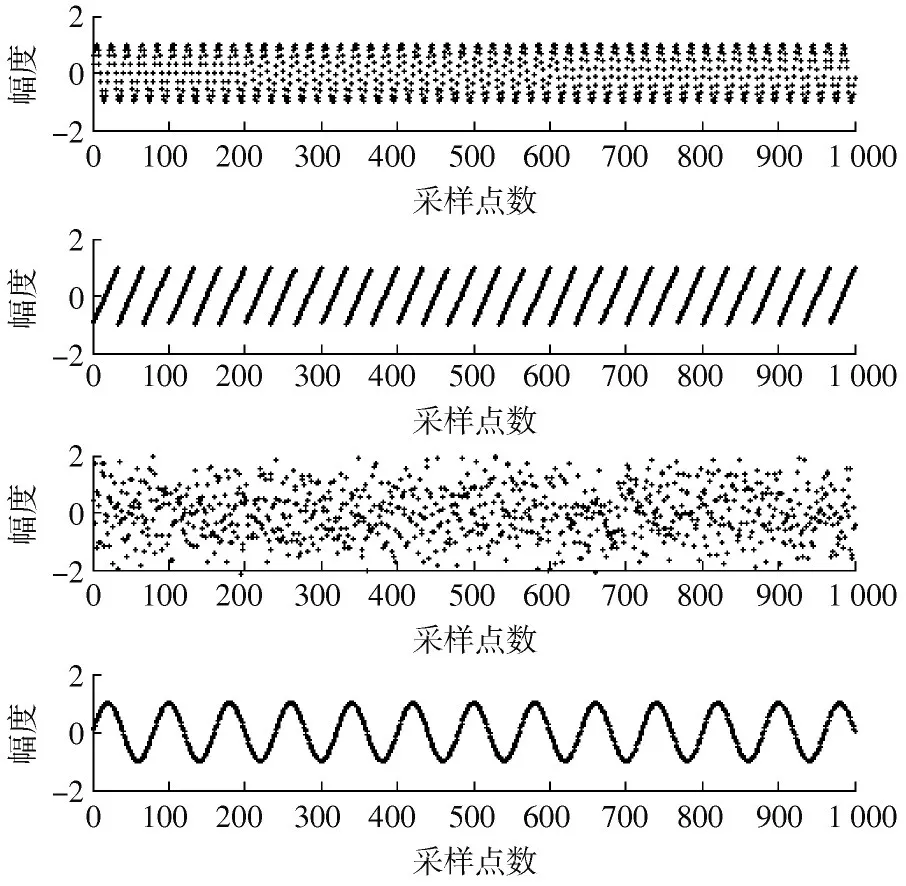
图1 源信号（一）

图2是线性混合信号，混合矩阵为服从区间[0，1]上均匀分布的4×4随机矩阵。

图2 混合信号（一）

图3是采用本文提出的盲信号分离算法对混合信号的分离结果。从图3中可直观地看出，该算法能对轻拖尾混合信号进行盲分离，分离效果较好。

图3 分离信号（一）

2）重拖尾与重拖尾混合信号的分离

图4中源信号依次是3个重拖尾信号和1个高斯白噪声信号。3个重拖尾信号来自于一段真实的语音信号。4个源信号的归一化峭度分别为：0.291，0.261，0.037和0，样本点取1 000。

图4 源信号（二）

图5是线性混合后的信号。混合矩阵为服从区间[0，1]上均匀分布的4×4随机矩阵。

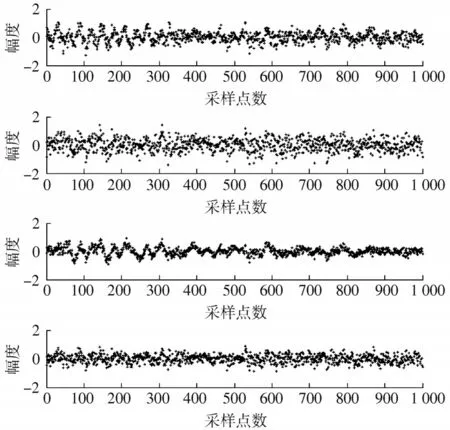
图5 混合信号（二）

图6是本文算法对重拖尾混合信号的盲分离结果。对比图4和图6可直观看出，分离信号的波形形状和源信号的基本一致，说明该算法能对重拖尾混合信号有效分离。

图6 分离信号（二）

3）重拖尾与轻拖尾混合信号的分离

图7中源信号依次是1个正弦信号（周期为80 s）、1个重拖尾信号、高斯白噪声信号和1个正弦信号（周期为100/3 s）。这个重拖尾信号来自一段真实的语音信号。4个源信号的归一化峭度分别为：-0.678，0.261，0和-1.926。样本点个数为1 000个。

图7 源信号（三）

图8是线性混合后的信号。混合矩阵为服从区间[0，1]上均匀分布的4×4随机矩阵。

图8 混合信号（三）

图9为本文提出的高斯混合模型盲信号分离算法对重拖尾与轻拖尾混合信号的分离结果，从图9可直观看出，混合信号分离前后的信号基本一致，算法能对重拖尾与轻拖尾混合信号有效分离。

图9 本文算法分离信号

图10为Kernel ICA算法对重拖尾与轻拖尾混合信号的分离结果，从图中可直观地看出，Kernel ICA基本可以恢复原始信号，但是分离效果差。

图10 Kernel ICA方法的分离信号

3 算法性能分析

选取源信号和恢复信号̂两者之间的差之比作为恢复信号的信噪比，衡量分离效果，即：

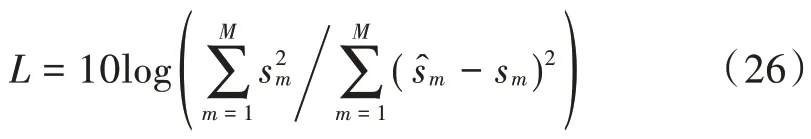
式中：s代表源信号；̂代表恢复信号。当恢复信号与源信号越接近时，信噪比值越大，则恢复效果越好。

为了验证本文提出算法的分离效果，对重拖尾信号（取自一段真实的语音信号）和轻拖尾信号（正弦信号，周期为80 s）的混合信号进行分离，样本数目由小到大共5个级别，采用Monte Carlo方法进行100次仿真实验。选取基于广义高斯模型的盲信号分离算法、经典的扩展最大熵算法（Extend-InforMax）、Kernel ICA算法进行对比。图11是4种算法分离性能对比图，从图中可以看出，本文提出的高斯混合模型的盲信号分离算法的分离效果最佳。

图11 算法性能分析效果图

4 结 论

盲信号分离算法性能的好坏取决于信号概率密度函数的估计准确度。本文采用高斯混合模型对信号的概率密度函数进行估计，使得信号的估计概率密度函数等于真实的概率密度函数，从而提高了算法的分离准确率。为了定量评价该算法的分离效果，选取分离信噪比作为评价指标。仿真结果证明，本文提出的盲信号分离算法分离信噪比较高，具有较好的分离效果。