平飞斜侧视双基雷达运动误差分析

林兰瑾， 何子述

(电子科技大学信息与通信工程学院， 四川成都 611731)

0 引言

双基雷达是指发射机和接收机安装在不同运动平台上的系统。它具有灵活的配置方式和成像模式(如平飞正侧视、平飞斜侧视等)，可以充分利用目标的散射特性来获取更多有用的信息。相比于传统的单基雷达，双基雷达更具有技术上的优点：1) 发射站可以远离被测地域，发射站生存能力得以提高；2) 接收站无源工作，敌方难以侦测，针对发射站的干扰，并不能影响接收站工作，因此这种体制具有良好的反侦察、抗干扰、抗截获能力；3)接收站不含高功率发射机，体积、重量大幅度减小，可以安装在RCS较小的无人机平台上，从而使接收站生存能力进一步提高。

在双基雷达系统中，由于收、发分离的特殊性，成像通常要求收发平台具有较好的运动状态，理想情况下为匀速直线运动状态。但是，在实际情况中，发射平台和接收平台受到大气环境中气流扰动、导航控制系统误差、机械以及执行任务等各方面不可预知因素的影响，不可能保持理想的匀速直线运动状态，其飞行轨迹会因为运动误差而发生变化，使得回波信号即使在矫正距离走动以后，时延走动误差和多普勒相位误差依然存在，造成多普勒相位移位和能量无法有效的积累，影响目标检测和成像。

双基雷达运动误差的来源很多，如飞行姿态的变化、雷达平台位置的改变或速度变化。飞行姿态的改变主要造成天线波束指向发生变化，可能造成双基雷达无法接收回波等影响。但是姿态误差不改变雷达平台的飞行轨迹，无法对回波距离历史产生影响。而雷达平台坐标误差会导致多普勒相位呈现二维空变特性，且走动矫正后的时延走动误差也不能忽略。速度误差的变化主要体现在大小和方向两个方面。在以往的研究中，也有不少学者做过讨论和分析。文献[9]在平飞正侧视模式下对速度误差进行了研究，但它仅分析了速度误差沿理想航线方向对成像的影响。文献[10]基于平飞正侧视模型，沿着3个方位(理想航线方向、俯仰方向、偏航方向)对速度误差进行了研究，但它只是定性地分析了速度误差对多普勒相位的影响。

基于以上的讨论，为了得到一般性结论，本文基于平飞斜侧视模型对速度误差进行了定量研究。考虑到收、发平台实际的飞行状态，将速度误差沿着3个方位进行了分解，即理想航线方向、俯仰方向和偏航方向。首先根据平台运动模型，分别给出了收发平台沿着理想航线方向、俯仰方向和偏航方向存在误差时的等效距离历史显性表达式；然后考虑速度误差给回波带来的两方面影响，即时延走动误差与多普勒相位误差，进而推导出了速度误差限定范围的解析表达式；最后通过仿真分析说明了速度误差对多普勒相位和信号能量积累的影响，为工程设计和实现奠定了理论基础。

1 双基雷达信号模型

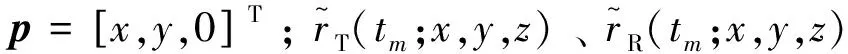
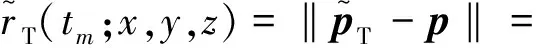
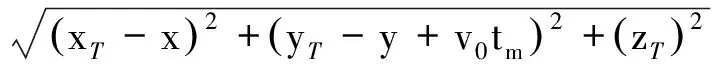
(1)

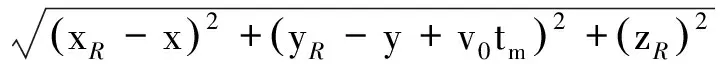
(2)

则目标点的双基距离历史为

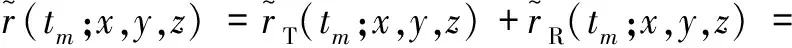
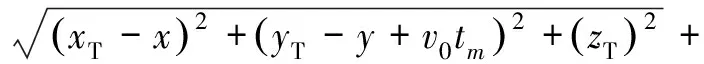
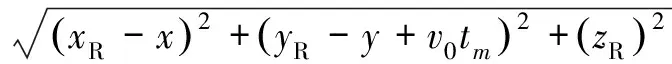
(3)

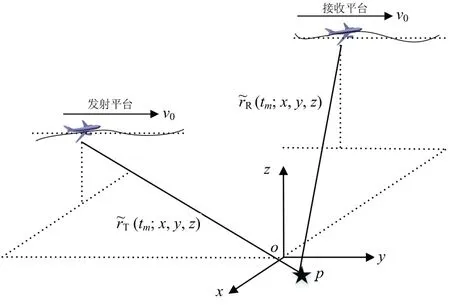
图1 机载双基雷达几何结构示意图

假设机载双基雷达发射信号为线性调频信号，根据双基距离历史和，脉压后接收信号的表达式为

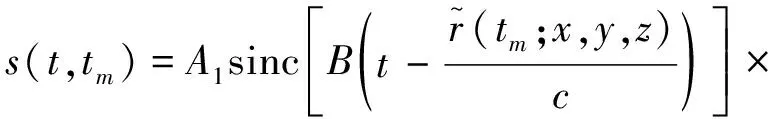
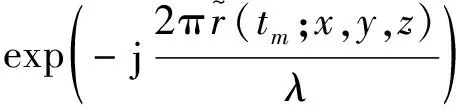
(4)

式中，为发射信号带宽，为脉压后的散射系数，为波长，包含了距离向快时间。

从式(4)可以看出，目标信号的回波包络位置随着慢时间而变化。当变化量超过距离分辨率时，将会产生距离走动，即积累时间内目标信号能量将分布在不同的距离单元内。此外，回波信号的相位是关于慢时间的二阶函数，会导致多普勒扩散。距离走动和多普勒扩散将会使得信号能量无法有效的积累，不利于后期的目标检测，因此在信号处理前矫正距离走动和消除多普勒频率扩散是非常重要的。

然而，在实际情况中，发射平台和接收平台不可能保持理想的匀速直线运动状态，其飞行轨迹会因为运动误差而发生变化，从而导致真实的距离历史和产生误差。假设距离历史运动误差为Δ(;,,)，则存在运动误差时的回波信号可以表示为

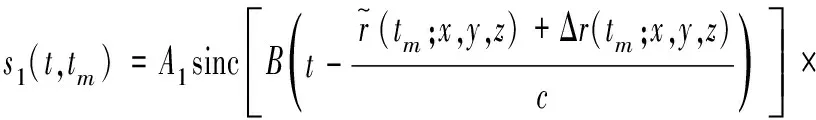
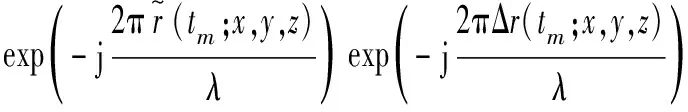
(5)

2 速度误差分析

考虑到载机实际的飞行状态，将速度误差沿着理想航线方向、俯仰方向和偏航方向进行分解，分别讨论3个方位上速度误差对信号的影响。

2.1 理想航线方向速度误差分析

理想航线方向上速度误差几何结构示意图如图2所示。我们定义ΔT和ΔR分别为发射平台和接收平台在理想航线上的速度误差，那发射站和接收站在理想航线上的速度误差运动方程可以表示为

T()=(+ΔT)

(6)

R()=(+ΔR)

(7)

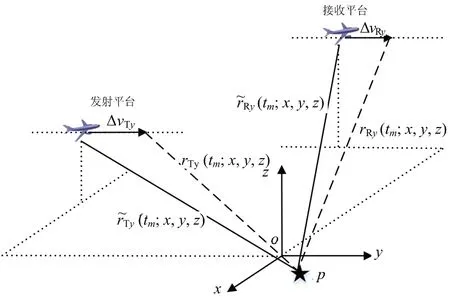
图2 理想航线方向速度误差几何结构示意图

将速度误差代入式(3)，则目标至收发站的距离历史和为

(;,,)=

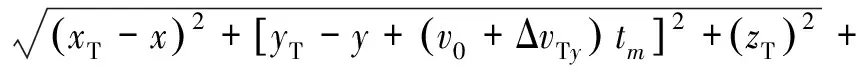
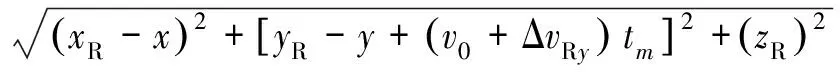
(8)

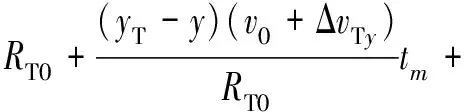
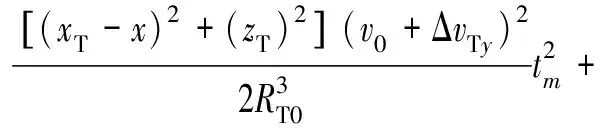
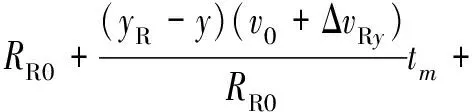
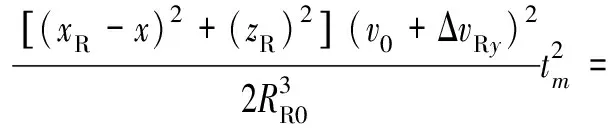
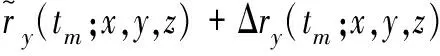
(9)

则距离历史和误差为

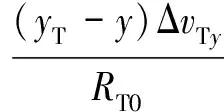
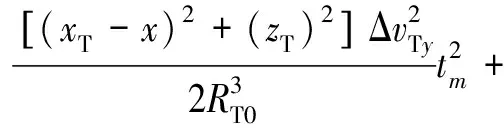
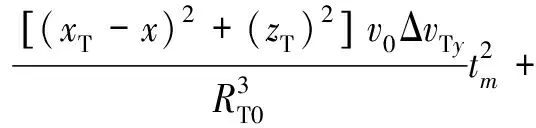
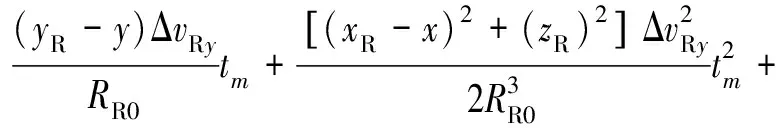
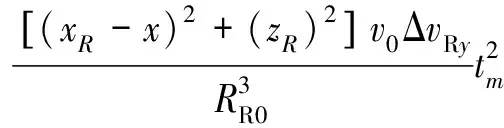
(10)

由于|ΔT|=，|ΔR|=，实际上|ΔT|和|ΔR|近似为0，因此，式(10)可以化简为

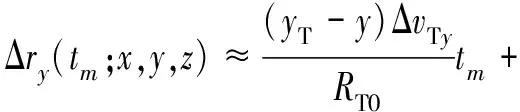
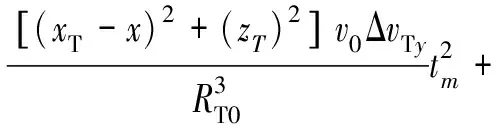
(11)

根据距离历史和误差，那么多普勒相位误差为

(12)

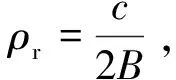
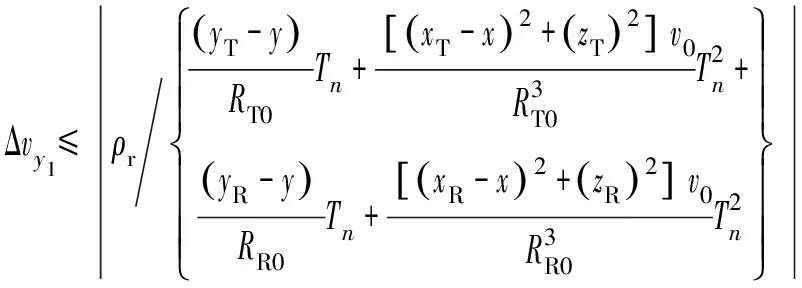
(13)

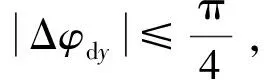
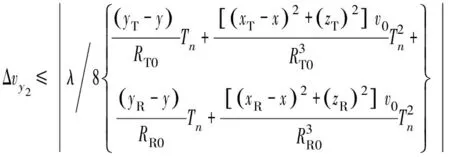
(14)

则理想航线方向上，速度误差的限定范围为Δ=min(Δ,Δ)。

2.2 俯仰方向速度误差分析

俯仰方向上的速度误差几何结构如图3所示。我们定义ΔT和ΔR分别为发射平台和接收平台在俯仰方向上的速度误差，那发射站和接收站在俯仰方向上的速度误差运动方程可以表示为

T()=ΔT

(15)

R()=ΔR

(16)

图3 俯仰方向速度误差几何结构示意图

将速度误差代入式(3)，则目标至收发站的距离历史和为

(;,,)=

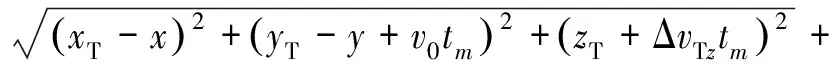
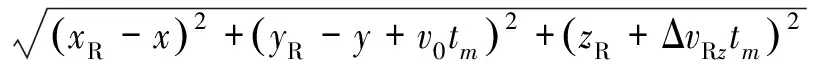
(17)

对上式按泰勒级数展开，可以得到

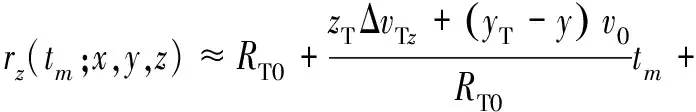
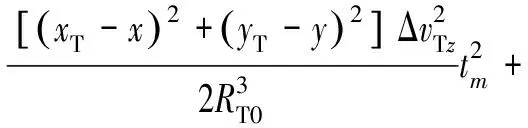
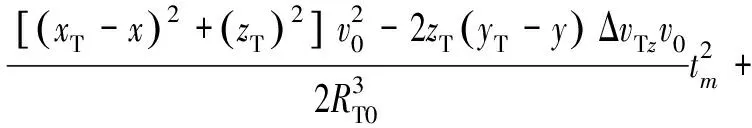
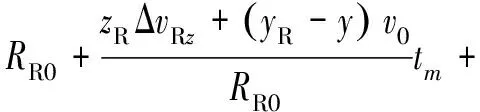
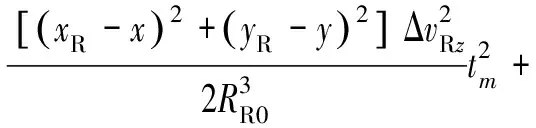
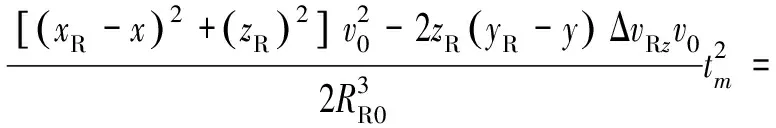
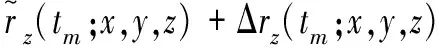
(18)

则距离历史和误差为

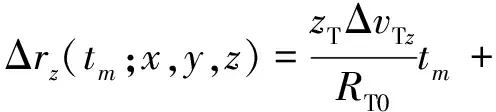
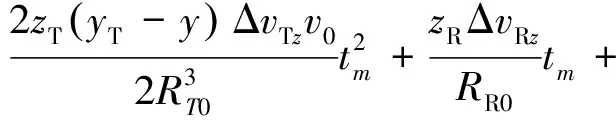
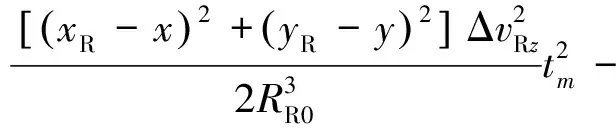
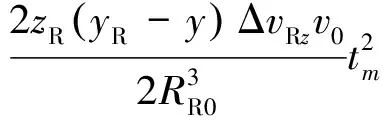
(19)

从上节分析，|ΔT|≈0，|ΔR|≈0，因此，式(19)可以化简为

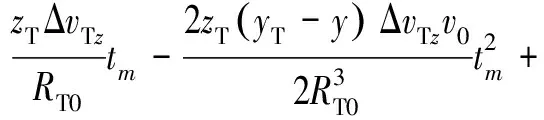
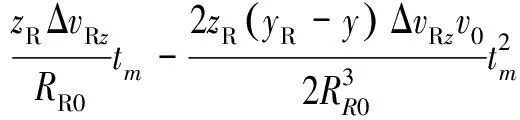
(20)

根据距离历史和误差，那么多普勒相位误差为

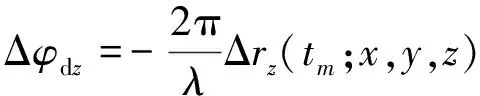
(21)

取Δ=max(ΔT,ΔR)，当时延走动误差不超过一个距离分辨单元时，距离维速度误差需要满足的限制条件：

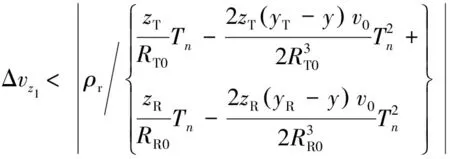
(22)

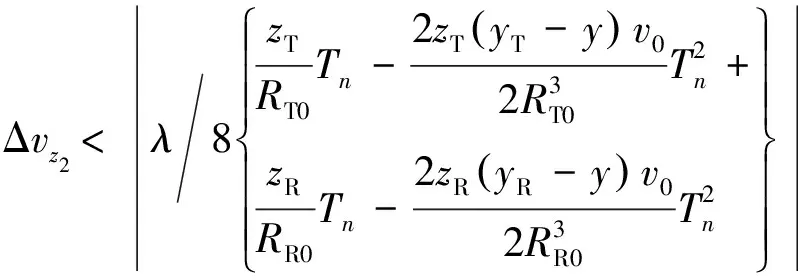
(23)

则俯仰方向上，速度误差的限定范围为Δ=min(Δ,Δ)。

2.3 偏航方向速度误差分析

偏航方向上的速度误差几何结构示意图如图 4所示。我们定义ΔT和ΔR分别为发射平台和接收平台在偏航方向上的速度误差，那发射站和接收站在偏航方向上的速度误差运动方程可以表示为

T()=ΔT

(24)

R()=ΔR

(25)

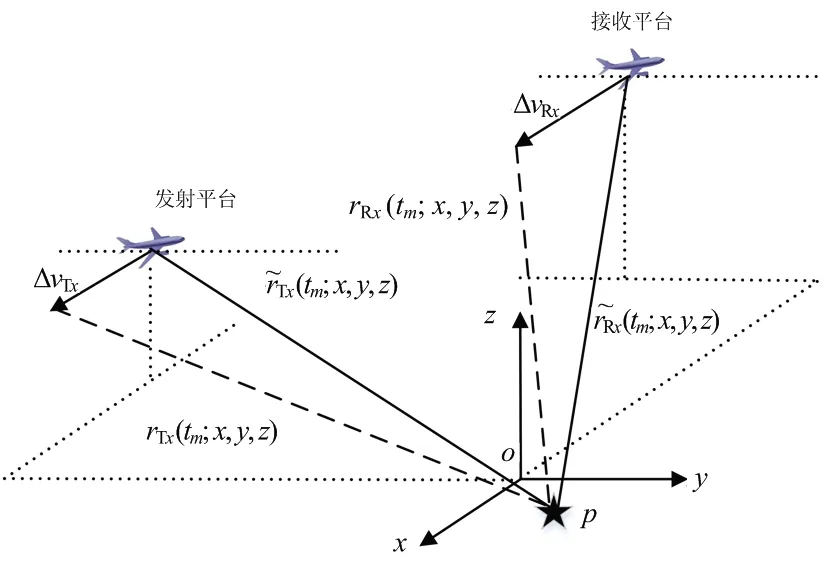
图4 偏航方向速度误差几何结构示意图

将速度误差代入式(3)，则目标至收发站的距离历史和为

(;,,)=

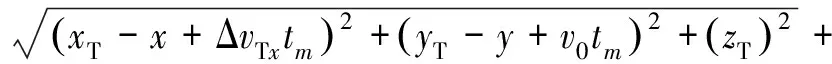
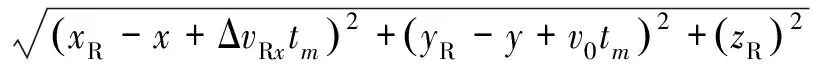
(26)

对上式按泰勒级数展开，可以得到

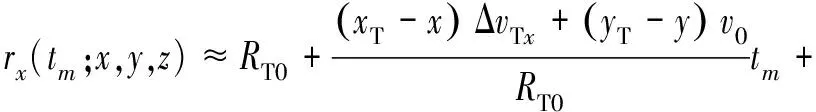
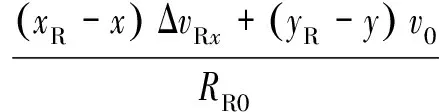
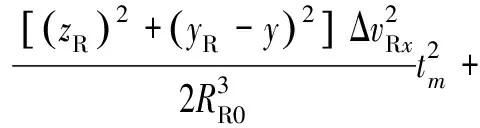
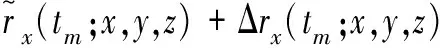
(27)

则距离历史和误差为

Δ(;,,)=

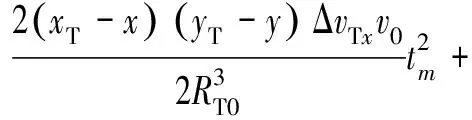
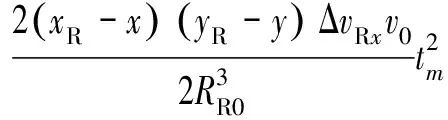
(28)

由于|ΔT|≈0，|ΔR|≈0，因此，式(28)可以化简为

Δ(;,,)≈

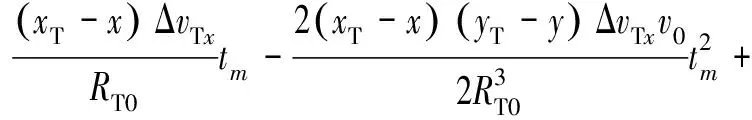
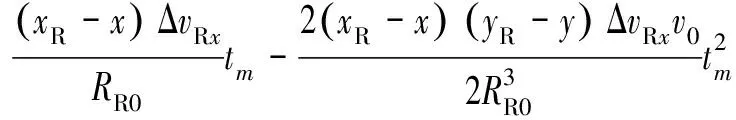
(29)

根据距离历史和误差，那么多普勒相位误差为

(30)

取Δ=max(ΔT,ΔR)， 时延走动误差不超过一个距离分辨单元时，距离维速度误差的限制条件需要满足：

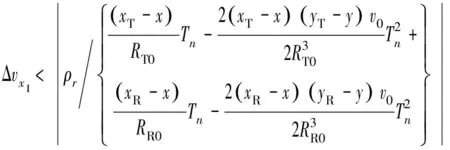
(31)

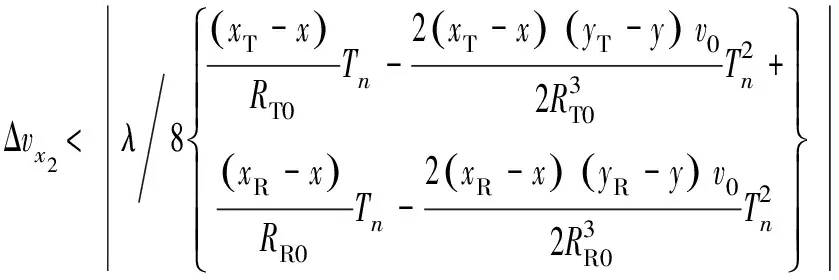
(32)

则偏航方向上，速度误差的限定范围为Δ=min(Δ,Δ)。

通过对速度误差沿着3个方位进行了定量的分析，可以得出以下的结论：1)速度误差的限定范围是与收发站位置坐标、目标位置坐标和平台运动速度相关的；2)积累时间越长，速度误差的容忍度越低；3)对比两个条件下所导出的速度误差限制范围，可以看出多普勒相位误差所导出的速度误差限制条件比时延走动误差所导出的速度误差限制条件更苛刻。

值得注意的是，上文所推导的3个方位的速度误差限制条件是比较严格的。实际上，有时发射站和接收站运动误差的速度差会抵消一部分最大运动误差带来的影响，反而使得双站的误差和比单站的误差要小一点，但即使误差值有所减小，其对时延走动和多普勒相位的影响依然存在。

3 仿 真

本节将通过仿真来验证所得结论。雷达参数和目标参数设置如表1所示。

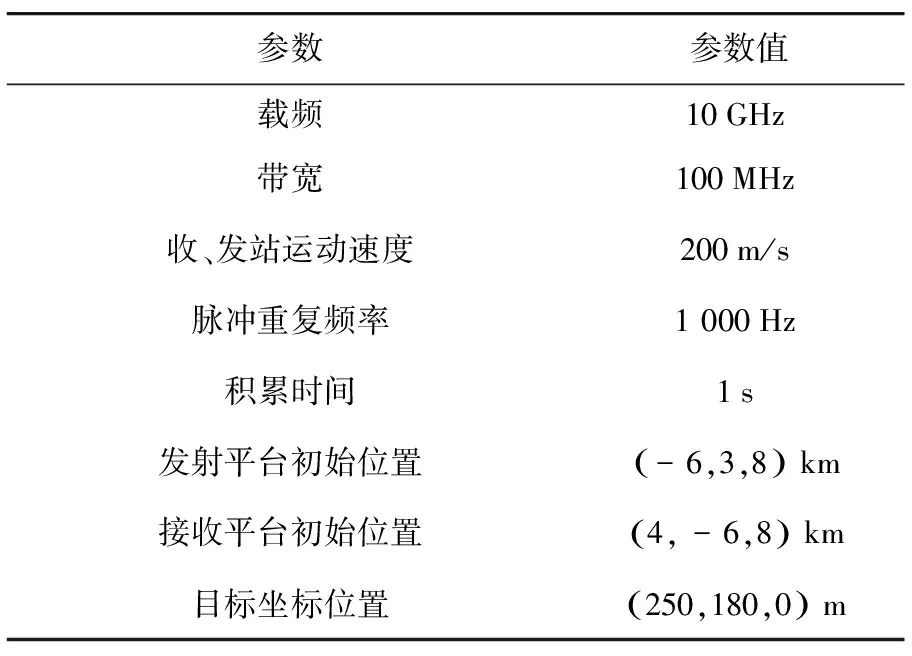
表1 雷达系统参数

将表1雷达系统参数的设置参数带入上节所推导出的速度误差限制条件，可以分别得出速度误差沿着3个方位的限定范围，如表 2所示。从表 2速度误差限定范围的数据可以看出，时延对速度误差的容忍度更高，而多普勒相位对速度误差的限制条件更苛刻；相比于理想航线方向和偏航方向，速度误差对俯仰方向的回波信号影响更大，速度误差的限制条件更苛刻。

表2 速度误差限定范围

根据表2速度误差限定范围给定的速度误差的限定范围，通过两组典型参数下的数值仿真，分析了速度误差对时延走动误差和多普勒相位误差的影响。两组速度误差的设置参数如表 3所示。

通过图5理想航线方向速度误差对回波信号的影响、图6俯仰方向速度误差对回波信号的影响和图7偏航方向速度误差对回波信号的影响的仿真结果，可以得出以下的结论：1) 当速度误差很小时，时延走动误差可以忽略，但多普勒相位误差依然存在；2) 当速度误差较大时，即使对回波信号进行了走动矫正，距离走动和多普勒扩散依然存在，会使得信号能量无法有效的积累；3) 沿理想航线方向速度误差主要引起主瓣位置偏移、主瓣峰值下降和主瓣展宽；4) 沿俯仰方向和偏航方向速度误差主要引起主瓣峰值下降和主瓣位置偏移；5) 沿俯仰方向速度误差的限制条件相比于其他两个方位要更苛刻，对误差的容忍度最低。

表3 速度误差仿真参数

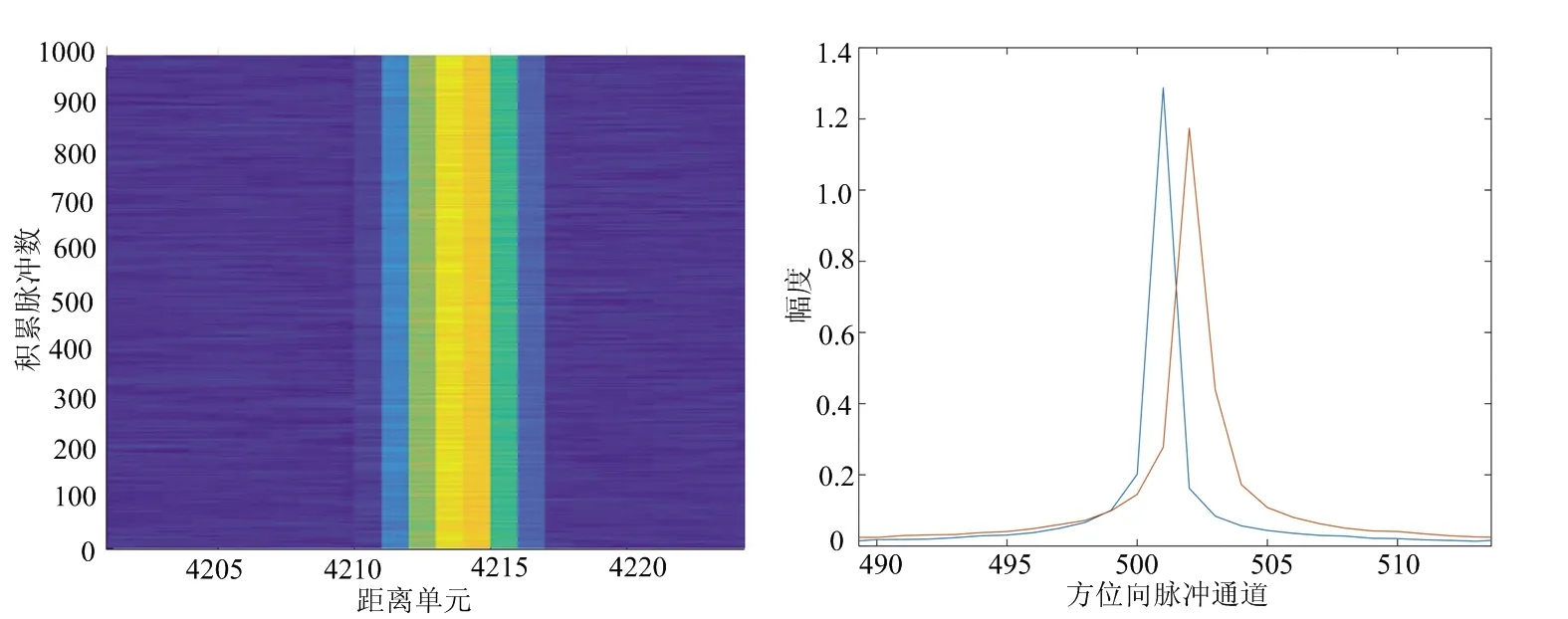
(a) 时延走动(0.05,0.1)m/s (b) 多普勒相位(0.05,0.1)m/s

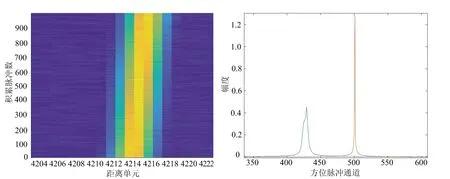
(c) 时延走动(8,0.1)m/s (d) 多普勒相位(8,0.1)m/s图5 理想航线方向速度误差对回波信号的影响

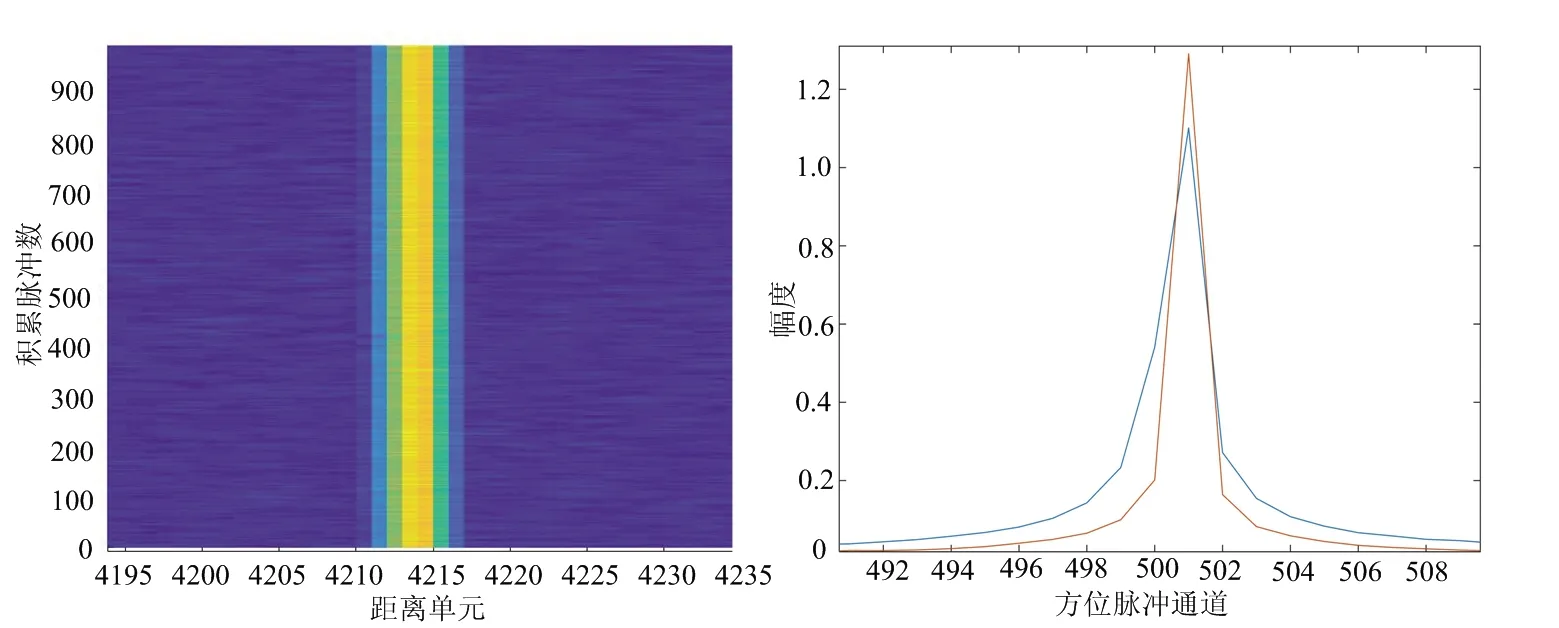
(a) 时延走动(0.001,0.007)m/s (b) 多普勒相位(0.001,0.007)m/s

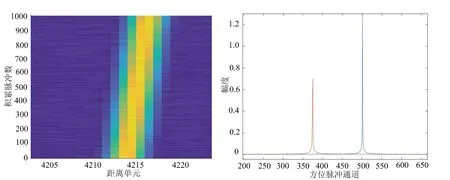
(c) 时延走动(5,0.007)m/s (d) 多普勒相位(5,0.007)m/s图6 俯仰方向速度误差对回波信号的影响

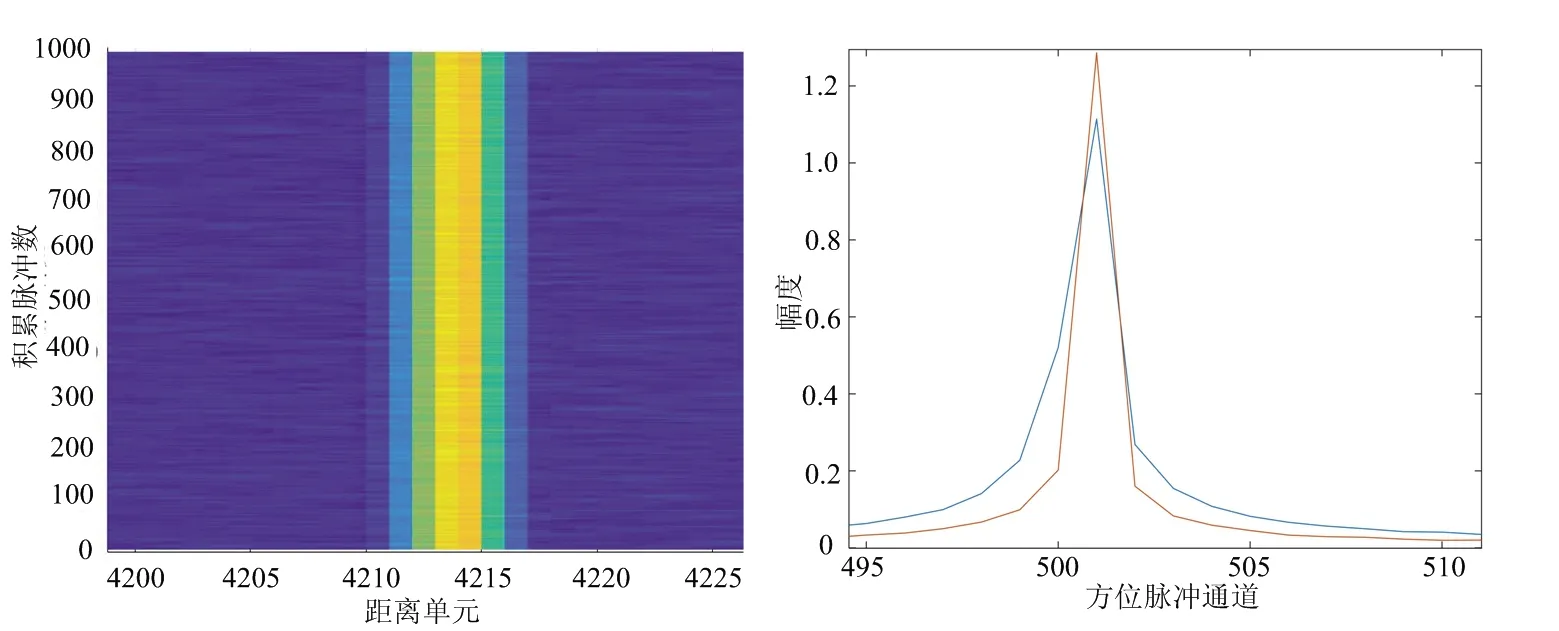
(a) 时延走动(0.05,0.01)m/s (b) 多普勒相位(0.05,0.01)m/s

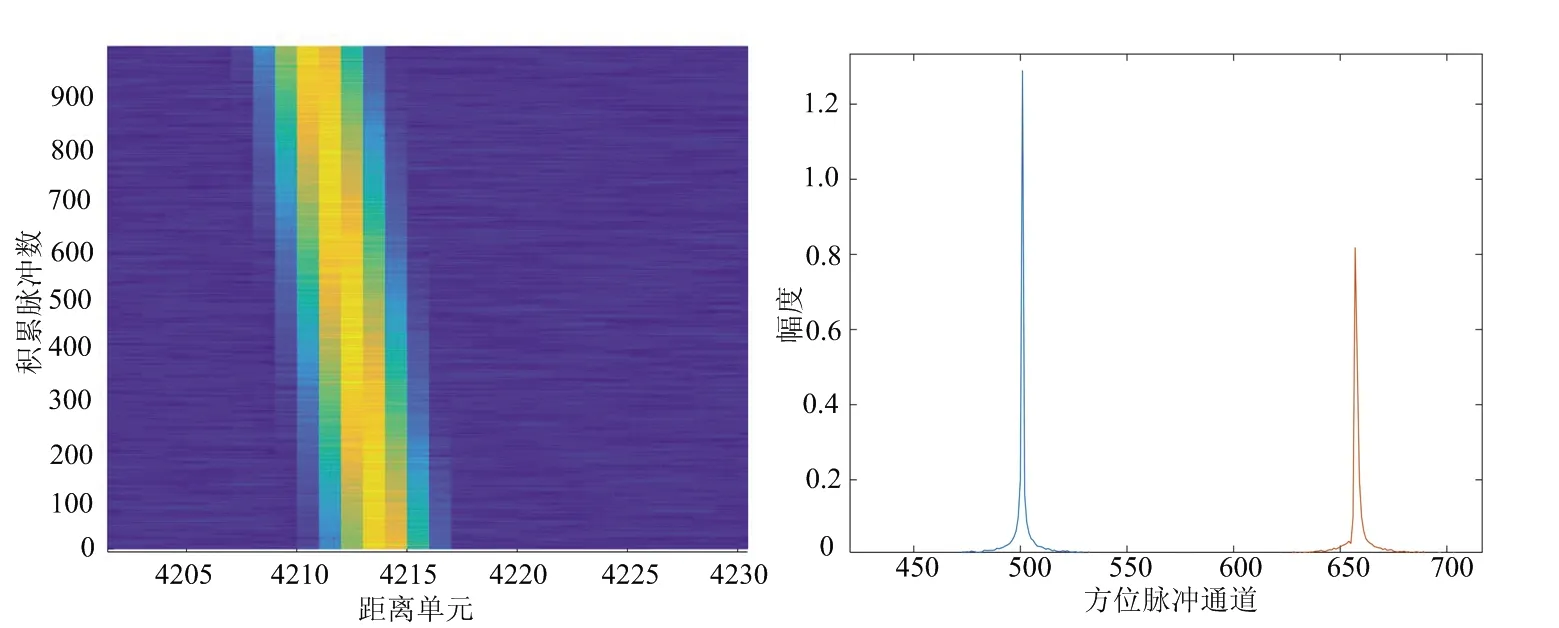
(c) 时延走动(8,0.01)m/s (d) 多普勒相位(8,0.01)m/s图7 偏航方向速度误差对回波信号的影响

4 结束语

本文基于双基雷达平飞斜侧视模型，沿着3个方位对速度误差分别进行了研究，并给出了速度误差沿着3个方位的限制条件解析表达式，为工程设计和实现提供了相关依据和参考。通过理论分析和仿真验证，证明了俯仰方向的速度误差限制条件相比于其他两个方位(理想航线方向和偏航方向)更为苛刻。此外，相比于时延走动，多普勒相位对速度误差的敏感度更高，对目标检测和成像的影响更大。