面向批量精密装配的显微特征定位
王晓东,于忠洋,徐 征,卢世勤,崔世鹏
(大连理工大学 机械工程学院,辽宁 大连 116023)
1 引 言
显微机器视觉的特征定位作为精密装配中重要的一环,为精密装配批量化、自动化发展提供了重要支撑。利用显微视觉引导操控精密机器人完成夹持、定位、放置是实现装配的主要途径,其精度要求一般在微米量级。虽然通过严格约束作业条件,目前显微成像测量及其运动控制能够满足这一要求。但是,生产中的结构振动、工具磨损、环境变化等均会改变装配状态,引起微小特征识别错误,从而影响装配效率和合格率,甚至中断装配流程,严重干扰自动化生产。因此,需要建立兼具强鲁棒性和高精度的特征定位算法。
经典的零件特征位置检测算法大致分为基于几何图形的配准和基于灰度或频谱信息的模板匹配。前者是通过梯度算子等获取边缘,利用最小二乘法等拟合获得图形,再与预存的理想图形对比计算出位置,在严格约束的条件下能够达到像素级的精度,但是它依赖具体图形,泛化性和灵活性不足。后者是通过目标样本的灰度或频谱分布与预存模板进行比较来确定特征姿态的,常用的模板判据有SIFT匹配[1-4]、SURF匹配[5-7]和灰度模板匹配[8-9]等。模板匹配算法对不同特征的泛化性高,但其精度易受光照变化和物体纹理波动的影响[10]。
近年来,机器学习成为研究热点,特别是基于卷积神经网络(Convolutional Neural Networks,CNN)的方法在显微视觉领域得到重视。Liang等[11]训练CNN估计微悬臂的位置和引导其沿轨迹运动;Jaradat等[12]借助CNN实现机械手视觉反馈控制;吴国伟等[13]将衍射图像与神经网络结合,改善表面形貌的三维重建精度;Li等[14]基于深度卷积网络引导机械手精确放置零件。虽然基于CNN的识别定位具有较强的泛化能力,但高精度CNN需要将大量样本在高性能计算机上长时间训练,而在一些特定工况,很难获得满足训练需求的样本量。此外,CNN识别误判尚难以分析和解释,使得此类算法应用到实际的批量精密装配时存在高不确定度风险。
支 持 向 量 机(Support Vector Machine,SVM)是轻量级的监督类机器学习方法,其本质是在特征空间上实现正负样本间隔最大的线性分类[15-16],常用于产品分选和缺陷检测。Liu等[17]结合SVM控制机器人引导工业废品分选和定向运输;Shehnaz等[18]结合梯度直方图和SVM分类器实现目标识别并对水果等进行分类;Fan等[19]建立了SVM的焊缝识别系统。SVM对计算资源和训练样本量要求相对较低,关键是要找到合理的特征。
本文面向批量精密装配对显微视觉引导的实际需求,建立了一种基于方向梯度直方图(Histogram of Oriented Gradient,HOG)和局部二值模式(Local Binary Pattern,LBP)复合图像特征的SVM方法,采用金字塔搜索策略提高效率,并在自行研制的精密装配设备上进行验证。结果表明,本方法具有良好的鲁棒性和精度,能满足批量精密装配的特征定位要求,并实现某微小执行器组件的自动化装配。
2 原理与方法
2.1 基本过程
本文使用HOG和LBP复合特征训练SVM并进行定位,过程如图1所示,具体步骤如下:
(1)对多幅零件图像进行图像预处理,形成原始训练集;
(2)从训练集中裁切处理出所需识别部分作为训练样本,并构建样本的图像金字塔以减少计算量;
(3)对训练样本使用HOG算子提取出边缘特征,使用LBP算子提取出纹理特征,并将二者组合;
(4)用金字塔每层的融合特征样本训练SVM;
(5)对目标图像进行滑动搜索并利用SVM计算其相似度值,寻找相似度最大的位置作为热点位置,实现准确定位。
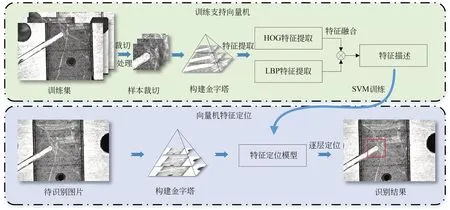
图1 特征定位向量机的训练及应用Fig.1 Training and implementation of feature localization vector machine
2.2 特征信息描述子的融合与分级处理
HOG特征用于描述图像边缘信息,优点是对光强变化不敏感。首先,计算每个像素的横向梯度Gx和纵向梯度Gy,再求出该像素处的梯度幅值G(x,y)和方向角度θ(x,y),即:
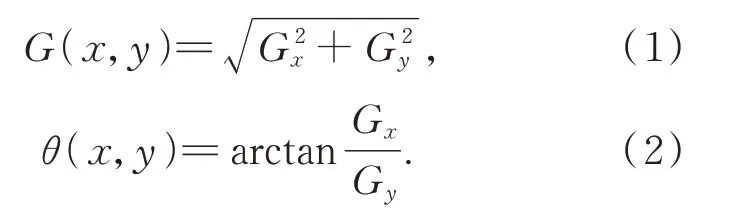
将图像分成若干胞元,统计每个胞元内像素的梯度信息,将梯度方向以梯度大小加权映射到固定的角度范围中,统计得到胞元的梯度统计直方图。将一定数量的胞元组合成块,将块内胞元的直方图串联起来,得到块内梯度信息的特征向量。然后进行归一化处理,以消除扰动影响,令ε为很小的标准化向量,使用式(3)归一化处理,计算出标准化向量。
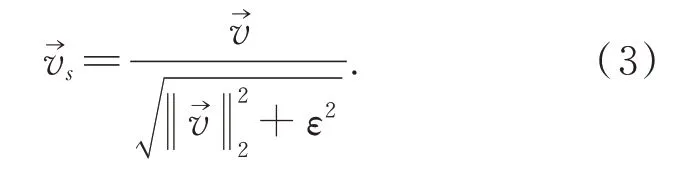
用滑动窗口遍历目标图像,计算每块中的特征描述向量,并连接形成HOG特征描述符。
LBP特征用来描述图像局部纹理。对于中心像素点(gcx,gcy),其灰度值为Sc,设定P个采样点,半径为R,对于其中的第k个采样点,其坐标为。对于邻域内未直接落在像素方格中央的采样点的灰度值,通过线性插值完成。计算得出各点的灰度值Sk后,与中心像素点相比较并进行二值化处理:
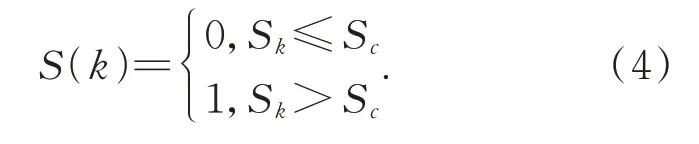
进而计算出不同采样点的加权和,得到该位置的LBP值:
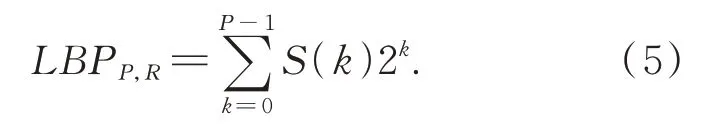
HOG特征对图像边缘有良好的不变性,而LBP特征则适合局部纹理描述。本文将二者融合,对微小零件进行综合描述,有助于提高鲁棒性和精度。融合采用向量化实现:设两个特征的维数为p和q,则输出特征的维数为p+q。
为提高效率,本文构建了图像金字塔的特征搜索策略,如图2所示。从分辨率最低的上层开始,使用滑动窗口搜索图像,选取相似度得分最高的部分为热点位置,随后以此热点位置为中心在下一层进行邻域局部搜索,直至分辨率最高的金字塔层。
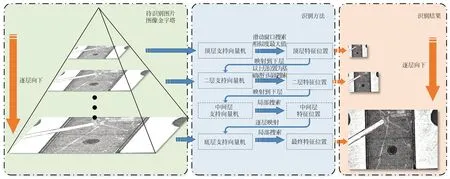
图2 特征位置搜索流程Fig.2 Searching process of feature location
2.3 SVM训练
主要训练步骤如下:
(1)拍摄多光照强度、多角度下的零件特征,采集多幅图像以增加分类器的鲁棒性。
(2)将所需识别特征部分裁切成同样尺寸,作为正样本,并选取背景部分作为负样本。
(3)构建正样本及负样本的图像金字塔,并将其进行上述计算生成对应的描述子。
(4)将每层金字塔的描述子连同对应的标签导入训练模型,进行最优超平面的查找计算,训练后得出分层特征识别模型。
3 自动化精密装配设备
实验在某微小执行器组件的自动化精密装配设备上进行。该设备能实现该组件上下料、夹持、吸附等系列操作,完成自动化装配。其主要结构如图3所示,包括:
(1)显微视觉测量模块:实现图像采集,由相机(分辨率为3 088×2 064)、镜头(1×)、光源和搭载光学元件的3轴运动平台(单轴重复定位精度为0.5μm)组成。
(2)作业工作台模块:用于夹具的定位与装卡、零件位置的调整(重复定位精度为0.3μm)。
(3)上料机械臂模块:负责对组装夹具及待装配零件进行上料操作。
(4)装配作业模块:精密装配系统中的主要执行模块,负责零件拾取、搬运、对准、锁紧等精密操作,与作业工作台协同完成整体的零件装配操作。

图3 执行器组件精密装配设备Fig.3 Precise assembly equipment for actuator components
4 实验结果与分析
4.1 稳定性测试
特征定位算法应具有良好的单峰性,避免多峰现象对识别结果准确性的影响。将待测特征模板放置在工作台上,并控制精密测量模块自动对焦特征。使用上述算法识别,在识别到的特征点附近进行宽度为60像素的方形范围内逐像素的相似度计算,绘制相似度网格,以验证算法的稳定性。
4.1.1 无纹理边缘特征的识别单峰性
掩模板特征边缘清晰且无纹理干扰,背景与特征间差异明显。具体特征定位结果及相似度峰值如图4所示。对于任意的掩模板特征单峰性明显,部分特征峰值周围曲线存在一定波动,但仍保持良好的单峰性。
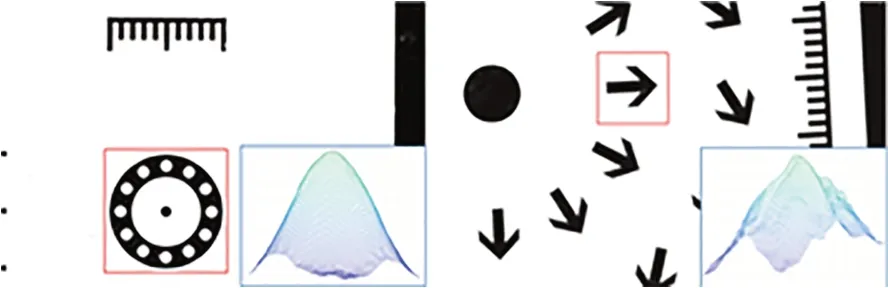
图4 掩模板特征定位Fig.4 Localization of mask template feature
4.1.2 表面纹理对单峰性的影响
选择具有明显纹理且边缘复杂的某执行器组件特征进行验证,如图5所示。对于较为复杂的特征,其峰值明显,非峰值处的相似度值与峰值处区分明显,且不存在多个峰值,仍保持良好的单峰性。
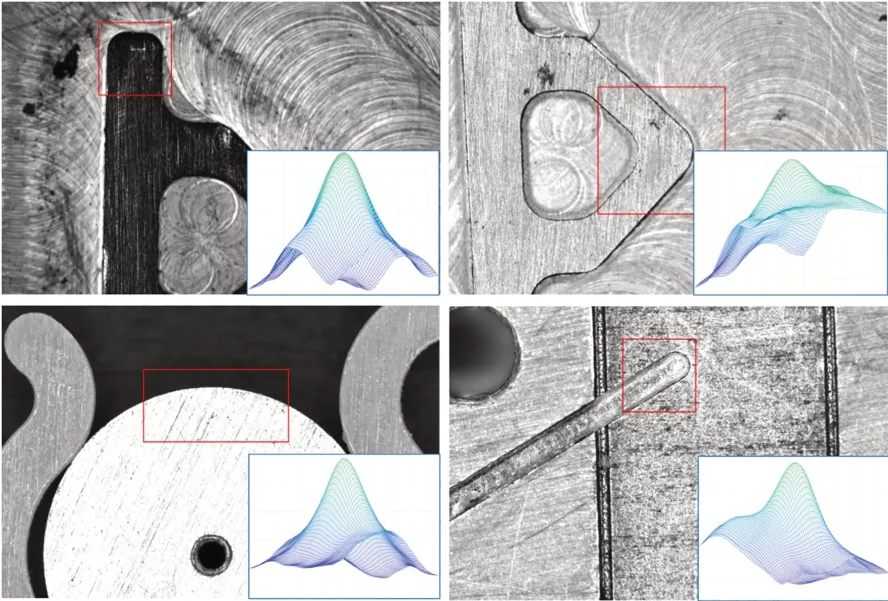
图5 执行器组件特征定位Fig.5 Localization of actuator components
4.1.3 光强变化对稳定性的影响
由于实际装配工况难以满足理想条件,在装配过程中会出现亮度偏移等情况,在批量装配中会对特征识别产生影响,因此采集多幅不同光强下的图像实验验证。选取同轴、环形光源的不同光强大小进行拍摄,对执行器底座圆柱特征进行定位分析,实验结果如图6所示。结果表明,在多种情况下,该定位算法都能够实现准确定位,有较好的鲁棒性,能够适应不同光强下的特征定位要求,且未出现多峰现象。
4.1.4 对比验证
图7为LBP特征及复合特征识别底座特征的对比。使用单一LBP特征进行识别时,其梯度较为平缓,峰值不明显,特征定位出现了较大的偏移;而复合特征单峰明显,峰值处梯度较大,保证了定位的准确性及唯一性。

图6 不同光强下特征定位Fig.6 Feature localization under various light intensities
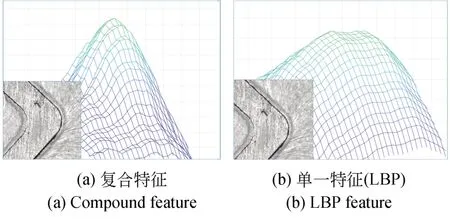
图7 复合特征与LBP特征对比Fig.7 Comparison of compound feature and LBP feature
图8为HOG特征及复合特征识别执行器组件表面纹理特征的对比。复合特征仍保持单峰性,梯度较大且峰值明显;而单一HOG特征出现多峰现象,易导致定位失败。
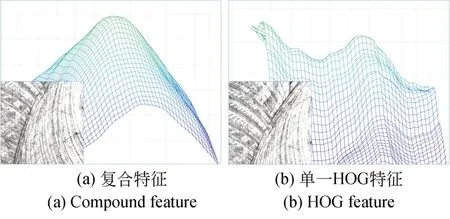
图8 复合特征与HOG特征对比Fig.8 Comparison of compound feature and HOG feature

表1 特征定位准确率对比Tab.1 Comparison of feature positioning accuracy
实验共采集103幅该执行器图像进行识别验证,表1为使用不同特征向量识别的正确率。结果表明,复合特征的定位鲁棒性及稳定性均优于单一特征。
4.2 准确性测试
在X和Y方向计算位置识别精度。将待识别零件放置于精密滑台上,对焦后保持相机位置固定不变。以精密滑台移动量为参照基准,每次同方向位移100μm并采集图像,在X,Y方向各采集10次。使用上述算法计算特征在相机视野中的位置,计算特征欧氏距离并与滑台位移比较评判准确度,结果如图9所示。4种特征中,X方向和Y方向的最大定位误差分别为3.93μm和3.78μm。该算法具有较高的重复精度,且识别精度皆优于4μm。
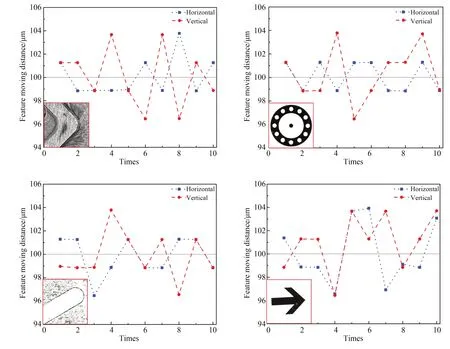
图9 X和Y方向特征定位精度Fig.9 Feature positioning accuracy in Xand Ydirections
4.3 批量装配实验
某执行器组件装配的同轴度与磁场均匀性密切相关。使用该自研设备进行其中两个组件的自动化批量装配,流程如图10所示,具体步骤如下:
(1)控制上料模块电动夹指夹持上料夹具,然后驱动单轴机器人进行上料操作;
(2)作业机械臂末端吸附起组件夹具,将其搬运至装配位置;
(3)通过视觉模块调用以上方法识别组件位置,调整机械臂和滑台位置进行对准操作;
(4)机械臂进行下压装配,通过力传感器伺服控制装配力。
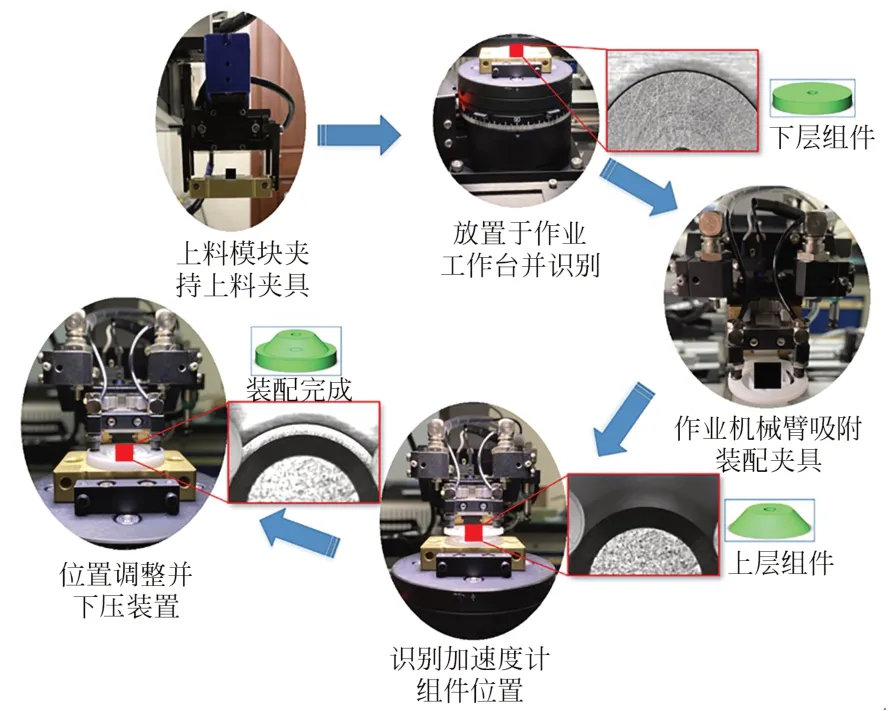
图10 某执行器组件的装配流程Fig.10 Assembly process of actuator components
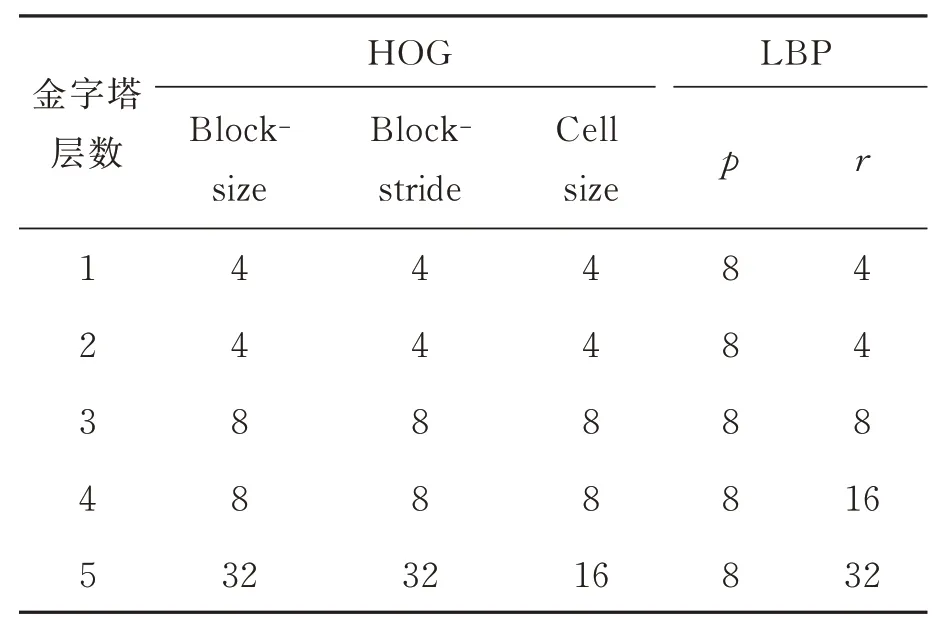
表2 实验参数Tab.2 Experimental parameters
装配后使用最小二乘法拟合出该组件边缘,计算装配完成后的同轴度作为装配误差。在能够辨别的光强范围内随机选取照明光强,模拟在亮度偏移情况下的装配条件;使用上料模块进行上下料操作,模拟振动等引起的零件位置偏差。连续进行10组装配,表2和表3为实验中使用的HOG算子及LBP算子参数以及实验数据。由上述结果可知:使用该识别方法引导装配,执行器组件的同轴度偏差X方向最大为4.54μm,均值为2.97μm;Y方向最大值为6.13μm,均值为3.81μm,圆心偏差最大值为6.94μm。在多种位置及光照强度下,本文方法均满足该执行器组件装配的同轴度要求。
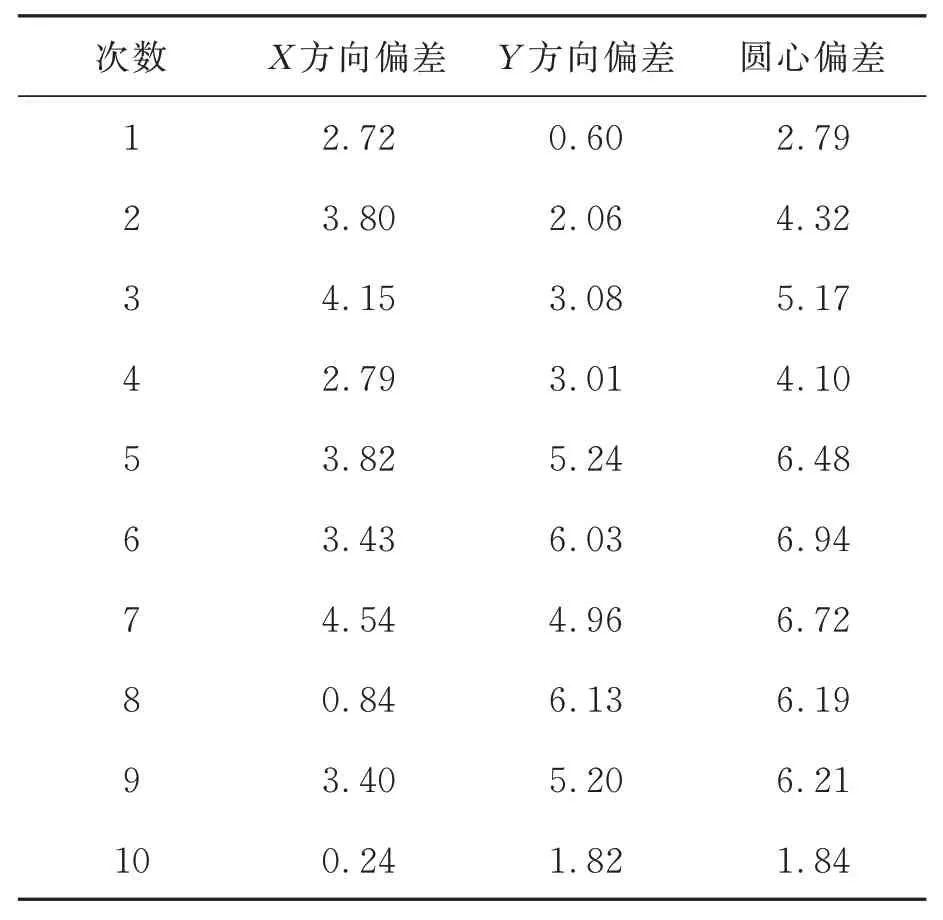
表3 装配实验结果Tab.3 Experimental results of assembly (μm)
5 结 论
本文提出基于融合特征的SVM的显微视觉定位算法,使用该方法实现某组件的批量自动化精密装配定位,并对其稳定性和精度进行了验证。不同的特征和光照条件下,本文方法获得的特征图具有良好单峰性,具有较高稳定性和抗干扰能力;将融合特征与单一特征进行对比,结果表明融合特征的识别准确率达到98%,高于单一特征;在准确性测试中,利用本文方法对以固定距离移动的特征定位并以精密滑台作为基准,其定位精度优于4μm;通过精密装配设备进行某执行器组件装配实验,实现该组件的批量化装配生产,最终的装配精度优于7μm,验证了该方法应用于批量精密装配的可行性。

