一种改进的FunkSVD算法

岳小琛,刘其成,牟春晓

(烟台大学计算机控制与工程学院,山东 烟台 264005)

随着大数据时代的发展,各平台的数据信息量越来越多,导致用户难以从海量数据中获取自己感兴趣的内容。因此,推荐系统应运而生,在电子商务、电影视频、社交网络、阅读、基于位置服务(外卖、打车)、个性化邮件、个性化广告等方面都发挥着重要作用[1-3]。推荐算法主要有基于内容的推荐算法、协同过滤的推荐算法、混合推荐算法三类,其中协同过滤推荐算法应用最为广泛[4]。

协同过滤推荐算法主要分为基于用户(user-based)的协同过滤[5]、基于项目(item-based)的协同过滤[6]以及基于模型(model based)的协同过滤[7]。基于模型的协同过滤算法主要通过机器学习和数据挖掘模型的思想来建模解决,逐渐成为当前研究的热点方向[8]。文献[9]提出了一种基于用户播放行为序列的个性化推荐策略,实现了视频网站的个性化推荐。

随着基于模型的推荐算法进一步发展,FunkSVD算法在推荐系统的研究中得到了广泛的应用[10],该算法解决了传统SVD算法计算速率慢以及需要手动补全缺失的值的问题。为了提高FunkSVD算法的准确率,文献[11]基于FunkSVD提出了一种矩阵因子分解的体系结构和方法,为矩阵中每项预测提供可靠性值,提高了算法的准确率,然而对于稀疏的矩阵效果不佳。文献[12]提出一种基于FunkSVD矩阵分解和相似度矩阵的推荐算法,提高了算法的准确率,但该算法有可能产生迭代振荡现象,陷入局部最优解,而非全局最优解。文献[13]提出了一种将用户社会关系信息和项目信息融合在一起的改进FunkSVD算法,提高了算法的准确率,然而存在数据稀疏的问题,亟待解决。

针对上述问题,本文提出了一种基于深度学习的推荐算法,以提高FunkSVD推荐算法的准确率。利用深度学习中的RMSProp算法对传统FunkSVD进行改进,避免陷入局部最优解的困境,解决了迭代振荡以及数据稀疏影响算法准确率的问题,从而提高了推荐的准确率。经民宿数据集的实验结果表明,本文提出的算法较传统算法有更高的准确率。

1 相关概念

1.1 传统FunkSVD算法

FunkSVD算法是在传统SVD算法面临计算效率问题时提出来的,解决了SVD算法中需要补全缺失的值的问题,思想简单,效果好,将基于模型中矩阵分解的推荐算法推到了新的高度,该算法在实际应用中使用也非常广泛。

FunkSVD算法不再是分解为三个矩阵,而是将期望矩阵R分解为两个低秩的用户矩阵P和物品矩阵Q,把用户和物品都映射到一个k维空间中,这个k维空间对应着k个隐因子。即将期望矩阵R如下进行分解:

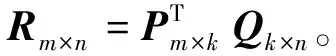
(1)

对于分解评分矩阵,实际上是应用线性回归的思想,用均方差作为目标函数,来寻找P和Q的最优值。然而,在实际中,为了防止过拟合,通常加上一个正则化项,针对已有的评分样本,可得到以下损失函数:

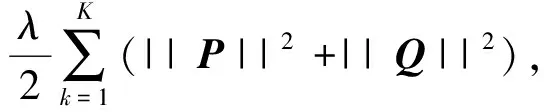
(2)

式中:rij为R中元素值,pik,qkj分别为P、Q中的元素值,λ为正则化系数。

传统FunkSVD算法采用梯度下降法求解损失函数。

首先对公式(2)中的P、Q求偏导可得

λpik=-2eijqkj+λpik,

(3)

λqkj=-2eijpkj+λqkj。

(4)

随后,根据梯度下降法更新初始P、Q,得到最优用户矩阵P以及最优物品矩阵Q。最后通过笛卡尔积计算得到更新后的评分矩阵。

1.2RMSProp算法

RMSProp算法是一种深度学习优化算法。该算法是梯度下降法的一种改进,它根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率,对低频的参数做较大的更新,对高频的参数做较小的更新,因此,对稀疏的数据表现很好[14]。RMSProp算法的梯度动量E[g2]是对平方项gt2的指数加权移动平均值,保证了各维度导数都在一个量级,也因此减小了梯度下降法的迭代振荡[15]。具体来说,给定超参数0≤γ<1、 迭代次数t>0时计算指数衰减平均值,如式(5):

(5)

其中:t为迭代次数,E[g2]t为损失函数在t时刻的累积的梯度动量,γ为衰减指数,gt为t时刻参数的梯度值。

RMSProp算法将目标函数自变量中每个元素的学习率按元素运算重新调整,然后更新自变量,如式(6):

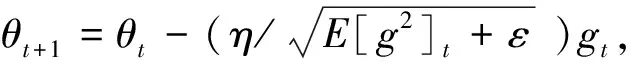
(6)

其中:θ为参数值,η为学习率,ε是为了维持数值稳定性而添加的常数,如10-6。

2 基于RMSProp算法改进的FunkS- VD算法

2.1 算法优化

针对传统FunkSVD算法准确率较低的问题,利用深度学习优化算法RMSProp对传统算法进行改进,改进后的算法对稀疏数据效果好,减小了迭代过程中振荡,提高了传统算法的准确率。

本文算法具体步骤如下:

(1) 准备好用户物品的评分矩阵R,每一条评分数据看作一条训练样本;

(2) 按照公式(1)将评分矩阵R分解为用户矩阵P和物品矩阵Q;

(4) 利用RMSProp算法取代梯度下降法更新P、Q中的元素值,具体步骤如下:

(7)

(8)

最后,将公式(3)、(4)计算结果以及公式(7)、(8)中求得的p、q指数衰减平均值代入公式(6)更新P、Q矩阵每个元素值,更新规则如式(9)、式(10):

(9)

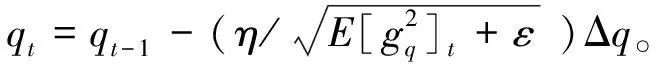
(10)

(6) 将上一步最终得到的最优矩阵P、Q的参数值pt、qt代入到公式(11)中,得到更新后的评分Ti。

(11)

2.2 算法设计

本文算法设计主要分为三部分:求解损失函数、更新迭代、评分预测。迭代更新是该算法的核心部分,在此过程中寻优找到P、Q最优值,进而进行评分预测。

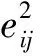
上述算法伪代码如算法1。

算法1 迭代更新

输入: 损失函数e, 衰减指数γ, 学习率η, 常数ε,极小值β。

输出: 最优值pt,qt。

for each value do

Δp=-2eq+λp

Δq=-2ep+λq

Ep=γEp+(1-γ)(Δp)2

Eq=γEq+(1-γ)(Δq)2

end for

for each value do

end for

end while

2.2.3 评分预测 利用上一步中最后得到的最优值进行评分预测,如公式(11),计算出最终的评分,最终输出评分矩阵Ti。

3 实验及结果分析

3.1 实验数据

本实验所用数据为网上下载的三个公开推荐算法数据集Movielens、OpenStreetMap和Last.fm,数据集的稀疏程度依次增大,都包括Item、User以及Rating。具体如表1。

表1 实验数据集

3.2 评价指标

评价一个推荐系统有多种指标,本文采用平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE),两种评价指标衡量算法的优劣。

MAE越小,说明预测值与真实值的差距越小,推荐精度越高,公式如下:

(12)

式中:rui′表示用户u对物品i的预测评分,rui表示用户u对物品i的实际评分,n为评分个数。

RMSE越小,推荐的准确率越高,公式如下:

(13)

式中:sui′表示用户u对物品i的预测评分,sui表示用户u对物品i的实际评分,n为评分个数。

3.3 实验分析

3.3.1 参数定义 本文算法参数较多,其中公式(1)中的k为特征数,通常为用户自定义[10];公式(2)中的λ为正则化参数,本文算法设为0.2[16];公式(5)中的衰减速率γ通常设为0.9,公式(6)中的学习率η通常设为0.000 1[15]。

3.3.2 参数调整 本文算法最主要的参数为公式(5)中的衰减速率γ。发现γ的取值为0.5时改进算法具有更高的准确率。采用Movielens数据集,迭代次数为10、20、30时,不同参数值的RMSE与MAE变化如图1。当迭代次数为30,采用不同数据集时,不同参数值的RMSE与MAE变化如表2。

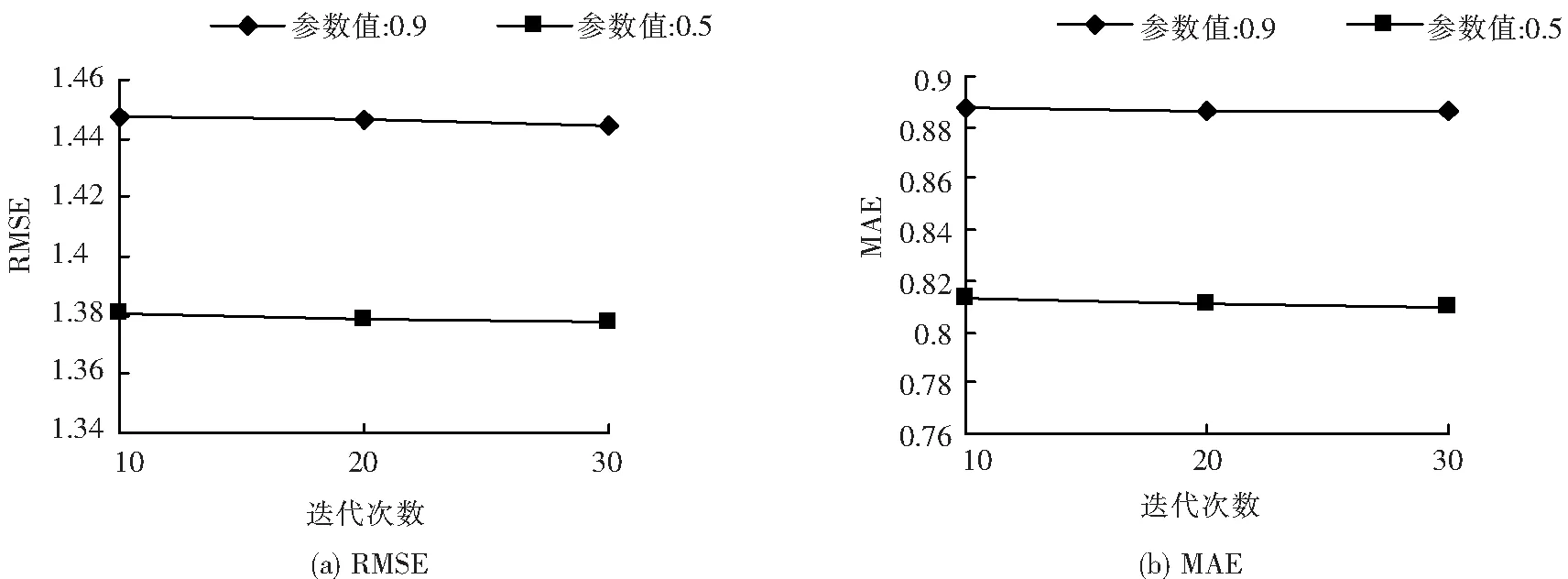
图1 不同迭代次数下不同参数值的RMSE和MAE

表2 不同数据集下不同参数的RMSE、MAE

由图1、表2可见,无论是数据集不变,改变迭代次数的情况下,还是迭代次数不变,改变数据集的情况下,参数值为0.5时算法的准确率更高。

3.4 算法对比

3.4.1 迭代次数 本文算法通过减轻传统FunkSVD算法中迭代振荡现象来提高算法的准确率,因此实验通过改变迭代次数将本文提出的算法与传统FunkSVD算法以及文献[11-12]中提出的改进算法进行对比,实验数据为Movielens,迭代次数为10、20、30。不同算法的RMSE和MAE变化如图2。

图2 不同算法的RMSE和MAE对比

由图2可见,在不同迭代次数下,本文算法较其他三种算法,准确率得到了提高。

3.4.2 数据稀疏性 本文提出的改进算法对稀疏的数据效果表现良好,在此基础上能够提高算法的准确率。因此,对不同稀疏程度的数据集进行了实验对比。Movielens、OpenStreetMap、Last.fm数据集稀疏程度依次增大。迭代次数取值为30。实验对比情况如图3。

由图3可知,随着数据集的稀疏性增大,四种算法的准确率均有所下降,然而本文算法准确率显著高于其他三种算法。因此,可以认为本文算法在处理稀疏数据时优于其他三种算法。

图3 不同稀疏度下RMSE和MAE对比

综上,结合分析实验结果表明,本文算法较传统FunkSVD算法、文献[11]改进算法、文献[12]改进算法具有更高的准确率,说明在提高准确率方面,通过改进数据稀疏以及迭代振荡是有效的,并且公式(5)中的参数取值为0.5、迭代次数为30时本文算法达到最优。

4 结束语

推荐系统的应用越来越广泛,基于模型的推荐算法也逐渐成为较为流行的算法之一,将深度学习与模型结合的推荐算法的研究也越来越多。本文为了提高传统FunkSVD算法的准确率,在数据稀疏以及迭代振荡方面用深度学习优化算法RMSProp对其进行了改进。实验结果表明,本文提出的算法的准确率有所提高,优于传统算法。

然而,本文算法在运行时间上较传统算法更慢,因此下一步的研究方向就是解决速率问题,以及如何将本文算法与其他算法结合使用,将其应用于更多实际问题上,实现更加有效的推荐算法。