考虑了不确定性及碳减排条件下的商砼企业配送规划

孙 杰，纪 颖,2

（1.上海理工大学 管理学院，上海 200093；2.上海大学 管理学院，上海 200444）

0 引言

随着国家经济的发展，城乡新起建筑如雨后春笋，广泛分布于各个角落。在建筑工程发展的过程中，商品混凝土(商砼)的使用对提高建筑施工的效率起到了关键作用。商砼搅拌站的出现，使得建筑施工地和原料供给地分离开来，既节约了场地布局，又对原料的质量起到了较好的保障作用。但同样，由于施工方和原料供应方的分离，而双方又都处于市区，使得商砼搅拌站和需求节点间的路径规划的重要性日益凸显。已有研究表明，科学有序的规划路径不但有利于节约商砼配送成本，还有利于提高工程施工的效率。在当前针对商砼的研究中，较多的学者从商砼的物化性质进行了分析，涉及透水混凝土性能，混凝土断裂性能，阻热降温性能，初始压实阶段应力-应变关系，仅有较少的学者对商砼的配送规划展开研究。商砼配送的研究涉及多个研究层面或者研究角度，现有的研究多数针对参数数据已知的情景，较少涉及不确定参数问题。相对于确定性条件下的规划设计，不确定条件下的研究更加符合现实场景。国内外专家学者做了大量研究。蔡焕芹，等通过遗传算法对混凝土配送问题进行研究，为现实场景提供决策支持。原野，等针对商品混凝土生产与调度问题展开研究以节约运输成本,。刘亚飞，等针对多搅拌站的配送问题提出了协同配送策略。林兴强，等以基于行程时间的可靠性车辆调度方法研究商砼的配送问题。针对商砼配送的研究往往仅仅涉及单一供应配送，或者单一需求站点的配送，较少的涉及多个供应站点的协同作用。

针对不确定参数问题研究的较为深入，模型应用领域也较多，包括应急管理问题，冷链物流问题，城市救援问题和能源运输问题等，但几乎没有发现研究涉及商砼配送规划的研究。最近不少学者援引鲁棒优化的方法处理不确定的参数规划问题，且取得了较好的研究实证价值。通过梳理文献发现，针对商砼配送规划的研究，还未发现学者通过鲁棒优化理论模型进行分析和研究，这也是本文的创新和贡献所在。

基于以上分析，提出了本研究的主要内容。首先，根据现实需求，构建多目标规划模型；其次，考虑到多目标规划模型间的相关性，本文将其归纳为两阶段线性优化模型；但由于不确定参数的干扰，线性优化模型在处理不确定参数问题时存在一定的弊端。因而，本文通过引入鲁棒优化的算法和理论，将TSLO模型拓展为TSRC模型，以抵御不确定性的影响，在不确定条件下展开研究。由于现实场景下的市场是充斥着随机性和不确定性的，因而开展随机不确定条件下的研究更具创新性。对于具体商砼配送管理企业而言，科学地规划运输车的时间和路径对于降低混凝土配送的成本具有重要的现实意义。

1 问题描述和模型建立

1.1 问题描述

针对市区商砼配送问题，基于实际场景，本文构建了由多个商砼搅拌站和多个需求节点构成的供应网络，如图1所示。其中，商砼搅拌站受产能约束的限制，仅仅可以为有限的需求节点提供配送服务，因此需要多个商砼搅拌站点的协同作业才能保障日常商砼需求。在综合考虑商砼配送过程中商砼搅拌站的固定成本，搅拌车的运输成本以及碳排放成本后，本文通过构建相应的数学规划模型进行理论分析。企业决策者往往面临着多目标决策问题：首先，从生存发展的角度分析，企业的首要目标为追求既定成本情况下的收益最大化(或给定综合效益情况下的支出费用最小化)；其次，企业还需把控运输车队的规模，提高运载率；最后，企业还要考虑目标客户的服务满意度，在既定现实资源约束的条件下追求最大化的服务满意度。

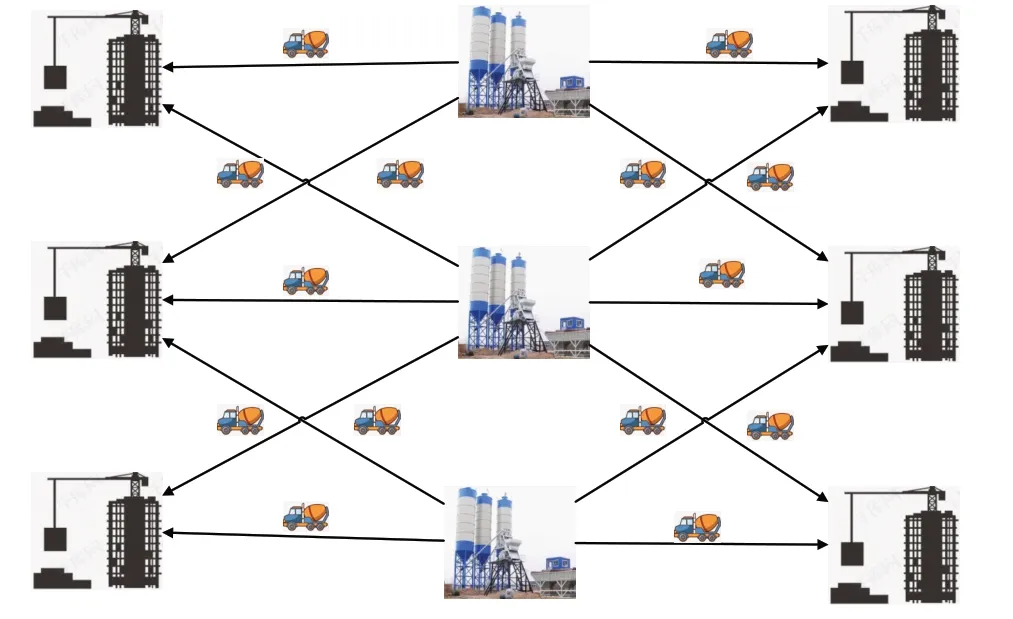
图1 多供应点多需求点的路径规划示意图

在普通车辆调度问题中加入时间窗约束，在客户要求的时间范围内提供服务。根据现实场景，本文考虑软、硬时间窗两个维度，具体情景如图2所示。软时间窗仅跟目标服务企业的规定有关，若规定时间为晚上的19:00-21:00，则提前送达会产生一定的等待成本，延迟送达会产生误工费用等，但这种风险较小因而称之为软时间窗，存在着上界和下界。硬时间窗受政策法规的限制，严禁违反。

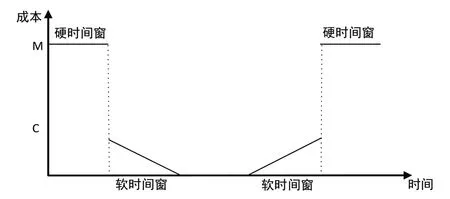
图2 时间窗示意图

模型假设：结合现实场景和数学建模的可行性，假设：

（1）节点位置和候选商砼搅拌站的位置已知；

（2）不得超过商砼搅拌站的最大产能约束；

（3）车辆同质，载货量和单位油耗已知；

（4）时间窗口是已知的；

（5）车辆采用直达运输配送模式。

1.2 多目标模型构建

目标1，整体运营成本的最小化。具体如下，目标表示为运输配送成本，分为固定成本c和可变成本，其中，可变成本包括能耗成本和碳排放成本。

约束条件函义，约束（4）表示所有目标节点的需求都必须满足；约束（5）表示时间窗约束，严格隶属于硬时间窗；约束（6）表示库存容量约束，库存不能高于上限；约束（7）表示仅有被选用的供应中心才会参与后续调配工作；约束（8）表示配送车辆的碳排放约束；约束（9）表示相关变量约束。

1.3 基本符号

本文符号及变量见表1。

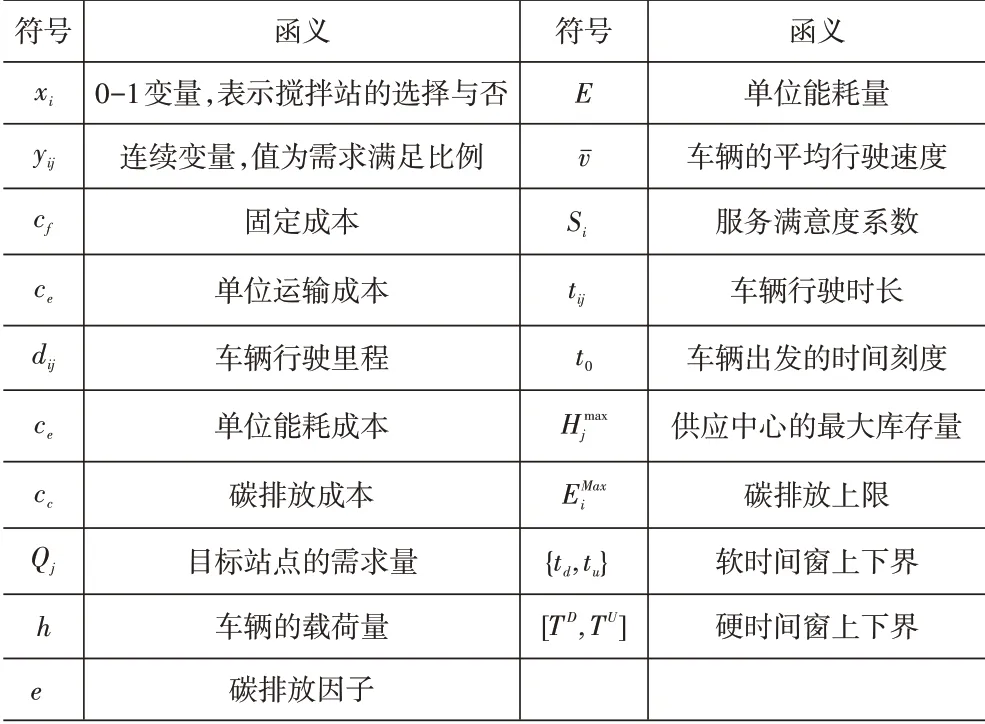
表1 基本符号变量涵义

2 模型拓展

考虑到多目标模型中的目标函数存在一定的关联性，将以上提出的多目标混合整数规划模型整合为两阶段整数规划模型。许多学者通过min-max 原则构建双目标模型的联立关系，并对模型的实用性进行了验证。援引学者的相关研究成果，对本节模型进行整合。其中，内层最大化问题为目标客户满意度最大化，外层问题为总体运营成本的最小化。

2.1 内层最大化问题

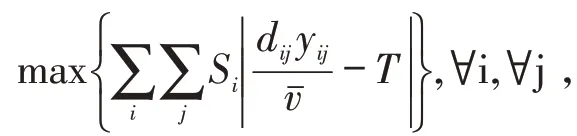
2.2 外层最小化运营成本

企业运营决策者作为理性的管理者，在保障了基本的基础运营平稳后，追求成本的最小化往往是其首选目标。外层最小化运营成本问题综合考虑企业的各项成本，包括固定成本，运输成本和碳排放成本与内层最大化满意度问题一样，也同时满足相应的约束条件。此外，由于在多目标混合整数规划模型中的f与车辆成本相关，本节模型中将其归为外层最大化问题的约束条件。

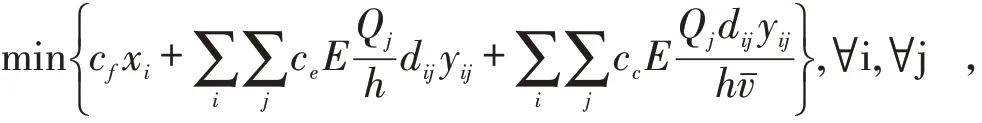
2.3 两阶段混合整数规划模型

根据以上内层最大化满意度问题和外层最小化成本问题，本节将以上多目标优化模型整合为两阶段整数规划模型，即：

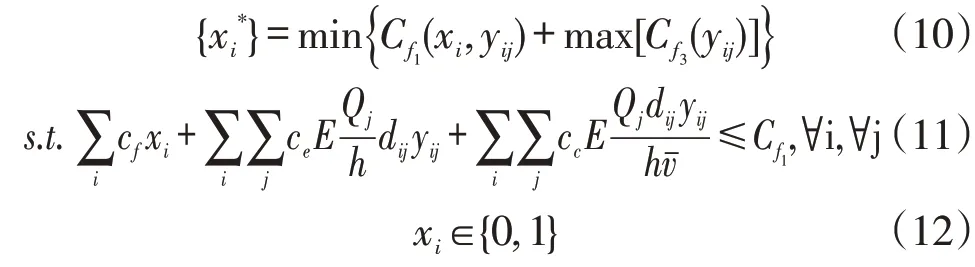
外层最小化成本问题是在服务满意度最大化的基础上的决策，其中，式（11）为预算成本约束，式（12）为变量类型约束。

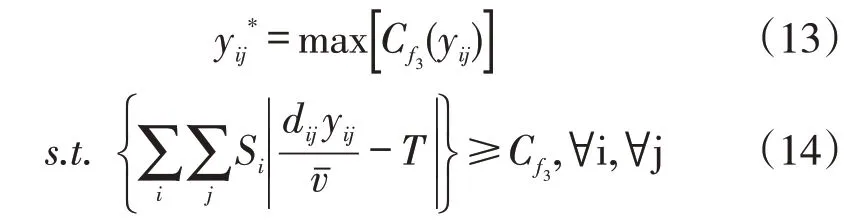
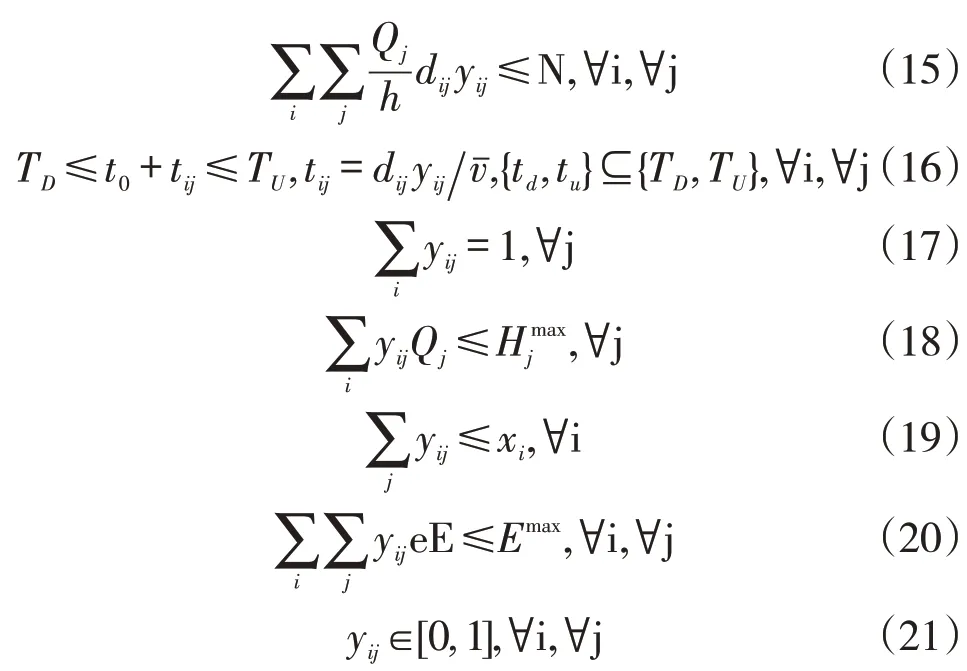
内层问题的决策目标式（13）是服务满意度最大化的服务满意度。式（14）是最低服务满意度要求；式（15）是最大车队数量规模约束；式（16）是时间窗约束；式（17）表示任意需求节点的需求都必须得到满足；式（18）是库存容量约束；式（19）是仅有被选中的仓库才可以参与后续运输任务；式（20）表示碳排放约束；式（21）为相关变量参数约束。

2.4 两阶段鲁棒优化模型

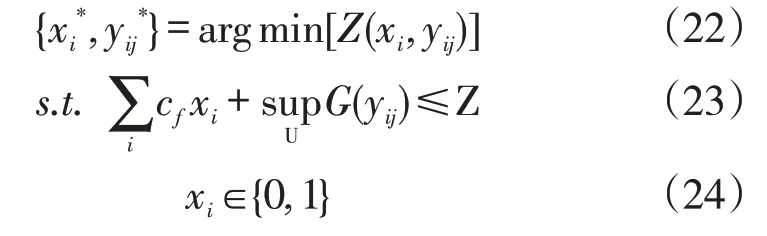
内层最大化满意度问题为决策的第二阶段，见式（25），其决策目标是最大限度的提高需求满意度。

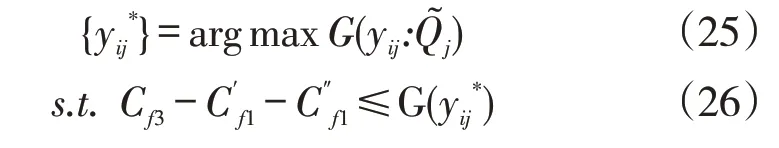
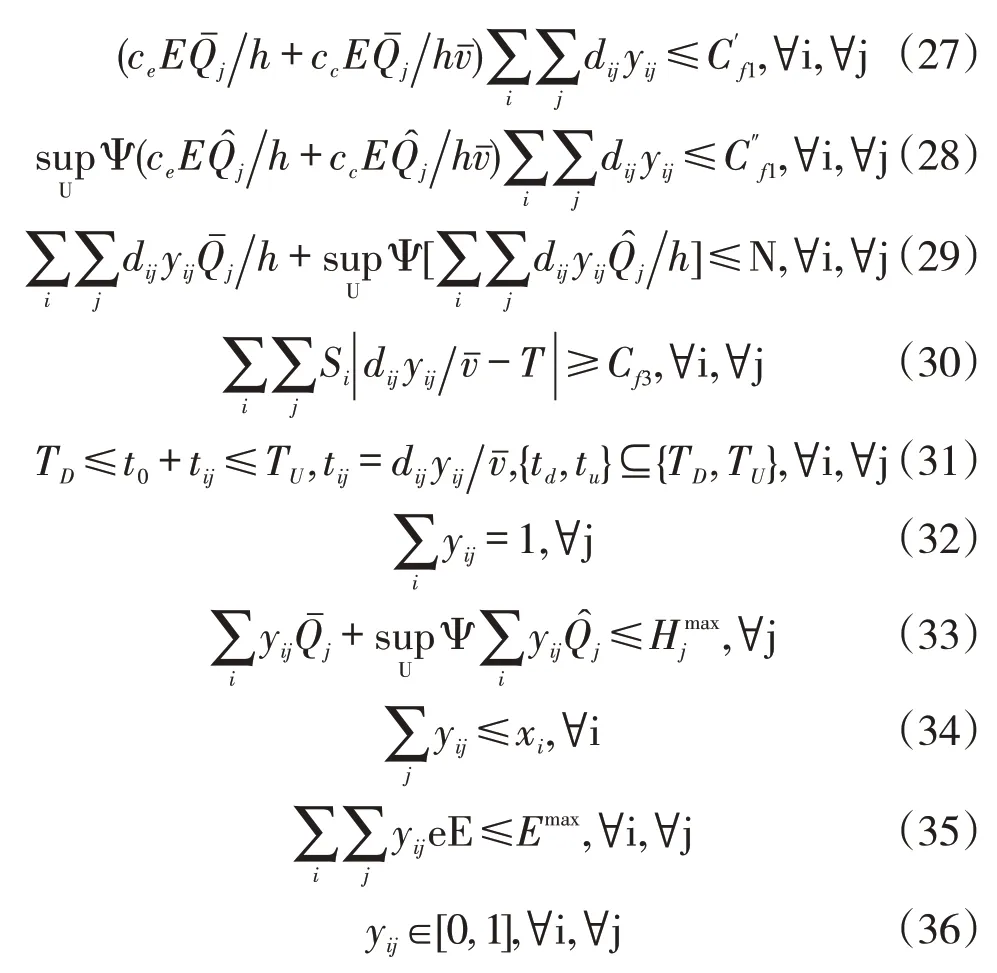
具体约束涵义：式（26）表示任意决策值不能高于决策变量取得最优时的取值；式（27）和式（28）分别表示基础需求参数条件下的预算约束和不确定参数条件下的预算约束；式（29）表示最大车队数量规模约束；式（30）是服务满意度约束；式（31）表示时间窗约束；式（32）表示任意需求节点的需求都必须得到满足；式（33）是名义需求参数和不确定需求参数影响下的库存容量约束；式（34）是仅有被选中的供应中心才可以参与后续运输任务；式（35）表示碳排放约束；式（36）为相关变量参数约束。

3 情景案例实验

商砼配送规划的合理性对保障工程进度起到了重要的作用。本文通过现实案例进行情景再现，研究所提出的模型在商砼配送规划中的实用性。根据实际场景，如图3所示，本文选取了某市的商砼配送作为案例。首先，根据实际场景，选取了四个站点作为候选商砼供应中心，分别为：恒基商砼、德济商砼、众诚砼业、天时商砼，用H1,H2,H3,H4 表示。需求节点为该市正在开发的商品房楼盘，分别为：宝龙世家、龙湖粼云上府、绿地映山风华、玖珑悦、梅里古都、新世界天悦、华润公元九里、太湖雍华府、富力山，建发金玥湾和山河万象楼盘，用Q1,Q2,...,Q11来表示。本节通过情景案例的形式检验所提出模型的实用性，根据情景案例的结果对模型进行分析，结果为相关决策者提供决策支持和管理发展建议。

3.1 基础数据

基础数据包括商砼搅拌站参数，运输车数据以及需求节点数据，见表2、表3。

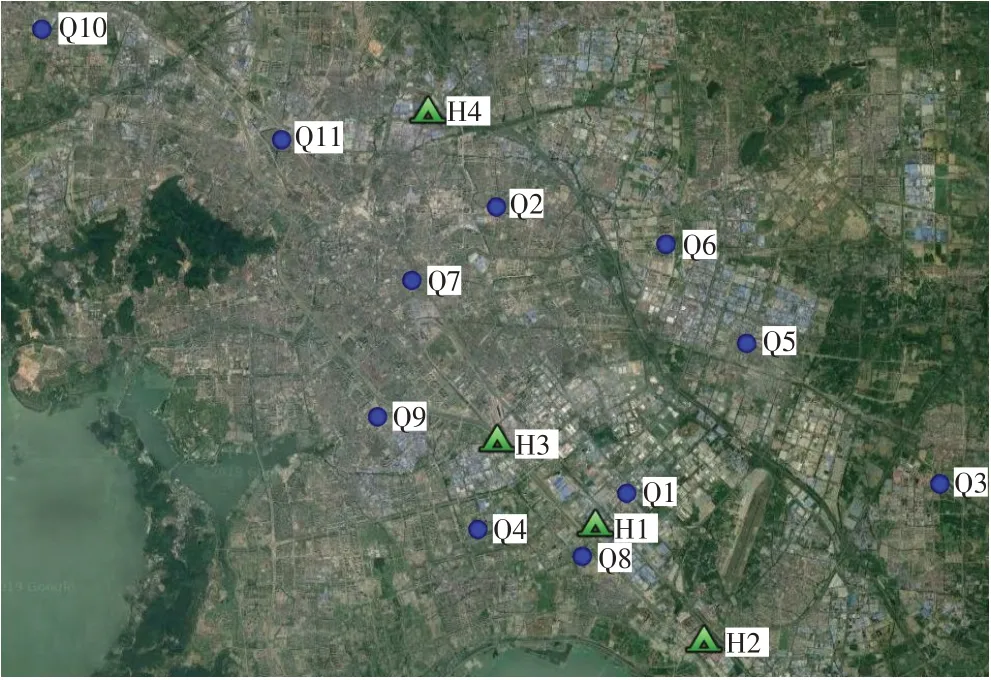
图3 商砼搅拌站和需求节点的地理区位

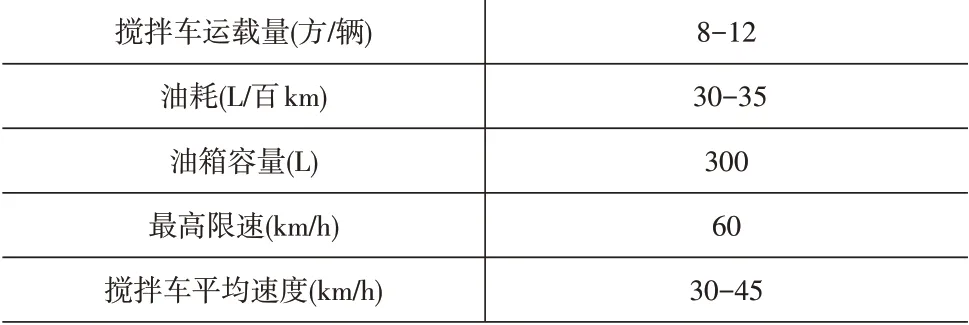
表2 基础数据信息

表3 商砼搅拌站及需求节点的数据

通过网页数据爬取技术，可以从谷歌地图直接获取站点间的真实距离，见表4。

表4 供应站与需求工地间距离

3.2 算法框架设计

基于以上基础数据值，以Matlab(R2020a)为编程平台设计求解框架，并且调用Gurobi(9.1.2)对模型进行求解。

为了保证情景案例的科学性，通过控制变量法将控制计算的环境相同，即在同一计算机内以相同运行环境(Windows 10,Core(TM) i5-8300H CPU @2.3GHz,RAM8GB,512G SSD)运行，具体算法步骤见表5。

表5 模型求解框架

4 模型参数分析

4.1 时间对比

图4 描述了TSLO 模型和TSRC 模型的计算效率情况。为保证实验的科学性，每个模型在同一计算机环境下进行100次运行，取累积时间值作为结果，比较模型的运行效率。可以发现，在求解器Gurobi的运算时间较短时，运行效率明显优于Cplex。数据对比可以发现，求解器Cplex 的平均时间约为Gurobi 的三倍。不同模型的运行时间是不同的，受计算的复杂度影响。MILP 模型结构简单，运行时间短，是固定的。由于随机参数的影响，MISP模型效率低且不稳定。值得注意的是，整体来看，在数据规模较小的情况下，MISP模型和MILP模型的总运算时间都不长，可以在短时间内解决运算方案，不会影响管理者在时间方面的决策。由于本文构建的案例结构比较简单，数据规模较小，时间长短差异不大。当模型中的约束和变量增加时，模型的运行效率可能会有所不同。因此，本文构建的模型应用于其他领域时，运行效率会受到模型规模的影响。可以看出，TSLO 模型的运行时间不受安全参数等级的影响，TSRC模型受影响较大，随着安全参数等级的提高，不论在哪种求解器中，运行的时间总是呈现出波动上升的趋势，这说明安全参数等级的增加增大了计算的复杂度。

4.2 成本的影响因素分析

图4 模型的时间效率对比(运行100次)

图5分析了不确定需求参数的波动对总成本的影响，以TSLO模型为参考基准(成本为100%)。可以发现，随着需求参数的波动性增大，也就是不确定集的边界扩大，与TSLO模型相比，TSRC模型的总成本呈现出不断上升的趋势(最大增幅约2%)，这就是鲁棒优化模型在处理不确定参数时所必须付出的鲁棒代价，即需要更高的成本削弱不确定参数的影响。在现实管理决策的过程中，管理者可以凭借历史数据估算相应的随机参数的分布情况，进一步就可以估算相应的运营成本。

图6从安全参数的角度分析了安全参数等级的提高对物流运输成本的影响，以TSLO模型的参数为基准(成本为100%)。可以发现，TSLO 模型的参数不受安全参数等级变化的影响，当然也无法解决不确定参数下的规划问题。TSRC模型中，随着参数等级的提高，模型的总成本呈现出严格单调递增的趋势，最大增幅约为4.2%，这是因安全参数等级的提高而付出的鲁棒代价。在市场化运作下的商砼配送企业中，由于不确定性信息的存在，使得成本的增长是在所难免的，企业决策者若能及时发现和规避不确定信息的干扰对成本的控制，则会起到较好的效果。

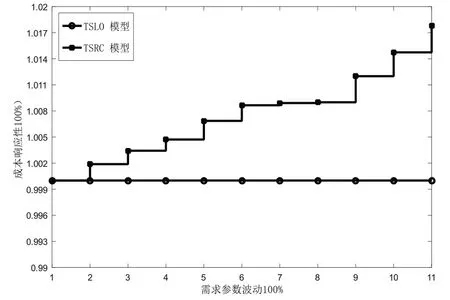
图5 成本对不确定参数波动的响应性

图6 成本对安全参数等级变化的响应性

4.3 商砼配送的路径规划设计

图7是根据模型计算得出的路径规划方案。以最小化运营成本为研究目标，在综合考虑了各项约束的情况下，路径规划示意图以商砼搅拌站为中心，呈现放射状的分布，每条线代表一条运输路径，每条运输路径上存在多辆车直达运输，由于单个车辆的运力远远满足不了需求节点的运输，因而路径上不存在转运或者TSP(旅行商)问题。在时间场景下，运输路径根据实际场景展开，图中规划仅显示是点和终点的相对关系。

图8描述了各个商砼搅拌站的服务占比情况。可以发现，在四个候选商砼搅拌站中，H3,H4 所承担的服务供应占比较大，在TSLO模型中，H3 和H4 供应占比均为31.8%；在TSRC 模型中，H3 的供应占比为34.1%，H4 的供应占比为29.6%。这说明这两个搅拌站的重要程度较高，与此同时，在TSRC模型中，H3 的比重有所增加而H4 的比重有所降低，从模型优化的角度分析，原因在于考虑了不确定参数条件下的问题时，为抵抗不确定参数的干扰，需要调整产业结构，以达到降低成本的效果。由于H3 站点距离需求节点更近，因而适当的增加其服务比重有利于优化产业结构，节约运营成本。

4.4 服务满意度

图9分析了碳税增加对服务满意度的影响，服务满意度以预设抵达时间和预设碳排放量的差额为基准进行计算，反映了各个模型的服务满意度对碳税波动的响应性。以基准碳税为基础，以10%为浮动区间，可以观察到随着碳税额的增加，服务满意度水平呈现出增加的趋势。这说明碳排放成本的增加对企业优化产业结构和优化运营模式起到了较好的诱导作用。这一研究结论可以为相关决策者提供管理建议，即适当的提高碳排放成本有利于实际运作活动中主动选择低碳发展路径，主动改变和革新能耗较高的管理策略，这对商砼配送企业是较好的低碳转型发展道路。

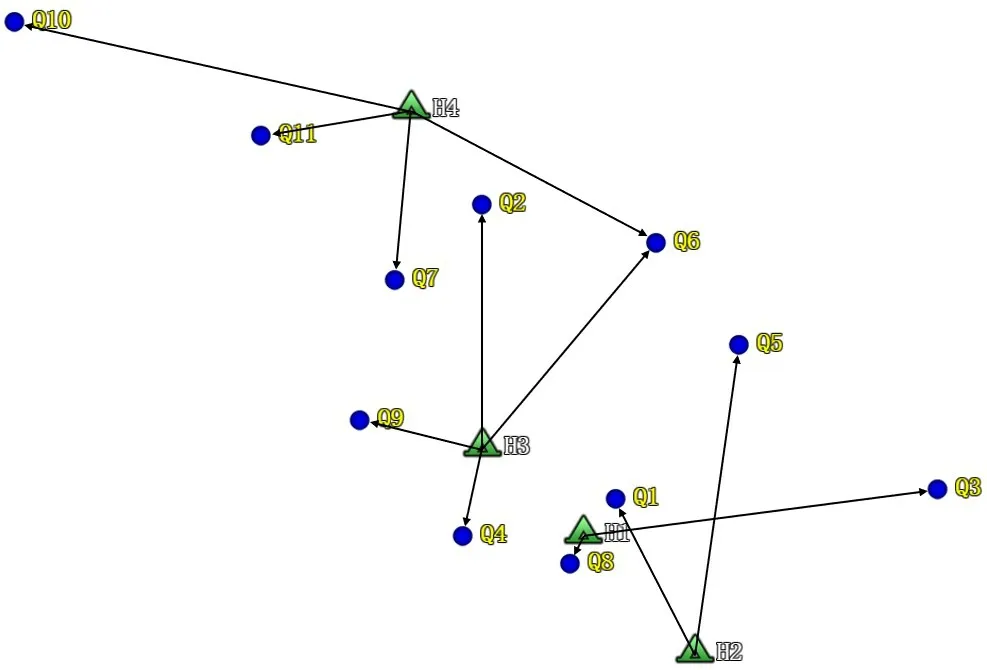
图7 商砼配送的路径规划设计

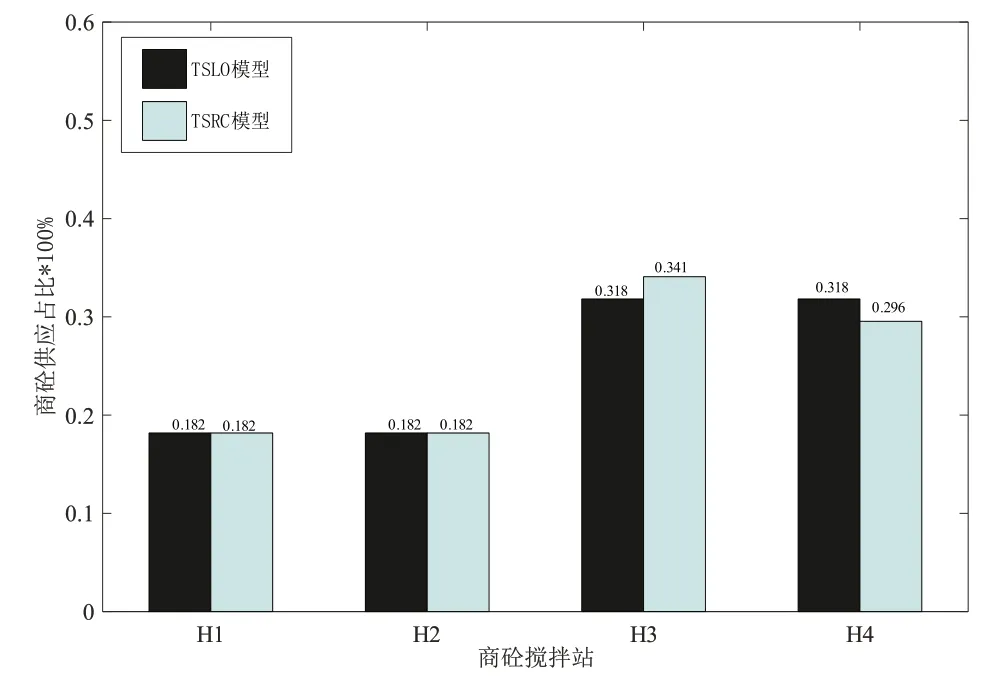
图8 四个商砼搅拌站供应服务占比

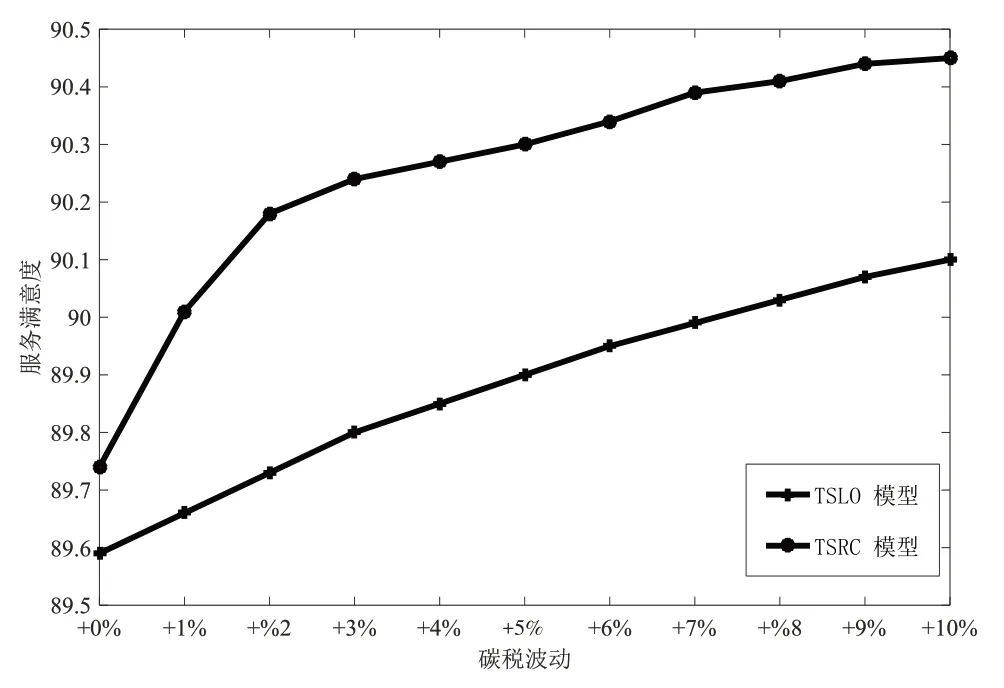
图9 碳税波动对服务水平的影响

5 结语

本文针对商砼配送作业管理的协同问题，在充分分析了商砼搅拌站固定成本、车辆的综合运输成本以及碳排放成本的基础上，将其归纳为多目标优化模型，在分析了多个目标函数的关联后，将其转化为两阶段线性优化模型。在考虑不确定参数的影响后，进一步将两阶段线性优化模型拓展为两阶段鲁棒等价模型，并通过案例验证了本文所提出模型算法的实用性和有效性。

本文研究的不足在于，前提假设是资源满足型企业的规划问题，未考虑供给不足的情况。此外，现实市场中还存在自建商砼搅拌站的大型企业，这些问题或许是今后的研究重点。