Effect of strain on charge density wave order in α-U

Liuhua Xie(谢刘桦) Hongkuan Yuan(袁宏宽) and Ruizhi Qiu(邱睿智)

1School of Physical Science and Technology,Southwest University,Chongqing 400715,China

2Institute of Materials,China Academy of Engineering Physics,Mianyang 621907,China

Keywords: uranium,charge density wave,strain effect,density-functional theory

1. Introduction

Charge density wave (CDW), which is a simple periodic reorganization of electronic charge accompanied by a periodic modulation of the atomic structure, is still poorly understood and continue to bear surprises.[1–9]This macroscopic quantum state occurs in a variety of materials including quasi-one-dimensional organic chain TTF-TCNG,[6]layered transition-metal chalcogenide,[3,7]and in particular,three-dimensional elemental metal uranium.[4]Uranium is the only element in the periodic table to exhibit a phase transition to CDW states at ambient pressure.[4]The existence of these low-temperature CDW states inα-uranium is wellestablished after several decades of thorough experimental work including the measurement of elastic constants,[10]lattice parameters,[11,12]phonon dispersion,[13,14]and neutron back-reflection.[15]The transitions into CDW states take place at 43 K, 37 K, and 22 K, and then the corresponding CDW phases are denoted asα1,α2, andα3.[4]The first transition fromαintoα1,involving only a doubling of the conventional unit cell ofα-U along theaaxis, is very simple and attracts considerable attention.[16–20]

Since the effect of strain on the CDW materials could in principles induces transitions into a different order, the relevant studies increase significantly in the past decade.[9,21–26]The application of strain could alter the band structure and thus provides the specific insight into the nature of a CDW phase, such as exploring the nature of Fermi surface nesting.[16,27]Unusual phenomena may emerge at the quantum critical points of strain-induced structural quantum phase transitions.[8]From the experimental point of view, strain is one of the few available handles that could be utilized to controllably and reversibly tune electronic structures. In bulk single crystal, strain can be applied by attaching materials to piezoelectric substrates. While in thin films,strain can be generated by using the lattice mismatch between the film and the substrate.

For uranium, the epitaxial thin film, in which the strain is present,has already led to the discovery of a wide range of new structural, magnetic, and electronic phenomena.[21,28–32]The hcp phase of uranium, which does no exist in the bulk,could be stabilized on Gd/Nb substrate.[31]All the allotropic phases of uranium are known as non-magnetic and confirmed by the theoretical calculation, while hcp-U is predicted to order magnetically. In addition,the CDW transition temperature increases from 43 K in the bulk to 120 K in the thin film of uranium on W.[21]Similar behavior could be found in the other CDW materials.[5,33,34]From the angle-resolved photoemission spectroscopy of uranium films on W(110),large spectral weight was observed around the Fermi level.[32]

Most of the theoretical works on the CDW of uranium have been within first-principles density-functional theory(DFT)[16,17,19,21,35,36]and mainly focus on the transition fromαtoα1.The pioneering work[16]constructed the model ofα1-U from displacing the atoms in the 2×1×1 supercell ofα-U(see Fig. 1) and employed the full-potential linearized augmented plane wave(FP-LAPW)method to evaluate the energy difference betweenα-U andα1-U.It was found that the small displacement (～0.028 °A) is energetically favorable and the energy gain is in agreement with the CDW transition temperature 43 K.In particular,the structural distortion could be interpreted using the nesting features of the Fermi surface inα-U.Phonon calculations using pseudopotential method also show that the energy of theΣ4phonon mode along [100] direction varies between negative and positive for different pressure[17]and strain.[21]However,despite of these abundant researches,relatively little is known regarding the effect of strain on the CDW order in the three-dimensional elemental metal U,rather than the other two-dimensional CDW materials.[9,22–26]

The main purpose of this work is a systematic investigation of the effect of the uniaxial strain on the CDW order inα-U from first-principles calculation in an attempt to establish a primary connection between strain and CDW order.It is found that the CDW charge order could be significantly enhanced by the tensile strain alongaorbaxis, and particularly the compressive strain alongcaxis. The rest of this paper is organized as follow. In Section 2,we present the computational details.Section 3 describes the results and gives our discussion. Our main conclusion is summarized in Section 4.

2. Computational details

The calculation of electronic structure, total energy,and force is performed within the framework of DFT[37,38]using the Perdew–Burke–Ernzerhof generalized gradient approximation.[39]The inclusion of relativistic effect is treated using spin–orbit coupling (SOC). Note that the main conclusion of this work could also been drawn from the DFT calculations of total energy without SOC. However, the nesting of Fermi surface could not be obtained from the calculation without SOC.The atomic structures in Fig.1 are constructed from the experimental lattice parameters[14,16]and used in the calculations. Here the qualitative conclusion on the strain effect on CDW order is independent of the lattice parameters.Note that a 2×1×1 supercell of conventional cell is used here forα-U to keep the number of atoms being equal to that inα1-U.To solve the Kohn–Sham equation,both the FP-LAPW method[40]and the projected augment wave(PAW)pseudopotential scheme[41,42]are used. On the one hand,the FP-LAPW method is applied here to accurately calculate the total energy and electronic structure. On the other hand,the evaluation of the force and the related phonon mode in uranium, which is the shortcoming of the FP-LAPW method,is carried out using the PAW pseudopotential scheme.[36,43–46]

The FP-LAPW method is implemented in the WIEN2k code.[47]The cutoff parameter isRMTKMAX=11.0, and the muffin-tin radius for theUatom is fixed at 2.45 Bohr. The Brillouin zone integration is done on a 13×16×13 mesh,resulting in 343kpoints in the irreducible wedge of the first Brillouin zone.

The VASP code[48]is used to employ the pseudopotential calculation,in which the plane wave basis is taken as 600 eV and the Brillouin zone integration is based on 11×11×11kpoint meshes. The total energies and Fermi surfaces from PAW calculations are compared with those from FP-LAPW(see Appendix A). The force constants are calculated within the framework of density-functional perturbation theory[49]and the phonon modes are obtained from the postprocessing using the phonopy package.[50]

3. Results and discussion

From the perspective of experiment,the most straightforward and measurable effect of strain on the CDW order inα-U is the modification of transition temperatureTCDW. Since the phase transition fromαtoα1is recognized to be first order,[12]TCDWis closely related to the energy difference betweenα1-U andα-U,[16]i.e.,the CDW formation energy,

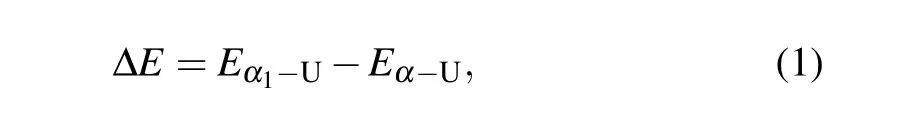
in whichEα1-UandEα-Uare the total energies per atom ofα1-U andα-U,respectively. Figure 2 plots the energy difference ΔEas a function of distortionu. The double-well shape,which is found in Ref.[16]and reproduced in our calculation,indicates thatα1-U with finite distortion is stable with respect to undistortedα-U. Our calculations are consistent with the results from Ref. [16] not only in the energy difference but also in the Fermi surface,which is shown in Fig.A1(see Appendix A).The topological change of the Fermi surface close to the pointU(1/2, 0, 1/2) in the reciprocal space is also shown here. This implies that one band splits at the Fermi level at the correspondingkpoints,which could be seen from the band structures in Fig.A2(see Appendix A).This kind of band splitting due to a symmetry breaking distortion is often referred as Peierls distortion.[1]In addition, let us note that the magnitude ofuto minimize the total energyumax～0.08 °A and the corresponding energy change ΔEmin～-1.8 meV per atom. The energy change is equivalent to 21 K,which is consistent with the experimental temperature of 43 K to transformα1-U toα-U.This quantitative discrepancy from that in Ref.[16]may result from the different computational parameters or lattice parameters. In particular, the specific lattice parameters are not given in the literature.[16]In our test calculations, the values ofumaxand ΔEminare very sensitive to the lattice parameters. Here for the sake of unambiguity and reproducibility,the experimental lattice parameters are used to show the effect of strain.

Now let us investigate the evolution of the CDW order ofα-U under the uniaxial compressive and tensile strains. Figure 3 shows the minimum CDW formation energy and the corresponding atomic displacement in the CDW phase as a function of uniaxial strain alonga,b, andcaxes. When the tensile strain is applied alongaandbaxes,the formation energy ΔEmingradually decreases and the maximum displacementumaxincreases,indicating that the CDW phase becomes more stable and the CDW transition temperatureTCDWincreases. In contrast, the compressive strain alongaandbaxes gradually suppresses the CDW stability andTCDWis very likely to decrease. This kind of strain effect,which is similar to the effect of pressure,[4,16,19,51]can be easily understood.By analogy, the effect of tensile strain is equivalent to that of negative pressure and the transition temperature would be lift.The compressive strain is analogous to the positive pressure and suppress the CDW transition. From the viewpoint of onedimensional atomic chain,[27]the tensile strain alongaaxis would increase the atomic distance and favor the Peierls transition.

Opposite behavior occurs for the strain alongcaxis. In this case, the CDW formation energy ΔEincreases with the increase of the tensile strain and decreases when the compressive strain is applied. This means that the CDW stability is suppressed by the tensile strain alongcaxis rather than the compressive strain alongcstrain. This result is quite counterintuitive and not easily understood. Here let us first attempt to discuss this anomalous behavior from the perspective of atomic structure. In Fig.4,theα-U structure in 2×2×2 supercell is presented. The structure can be conceived as a group of corrugated rectangular layers stacked in thebaxis.The degree of corrugation is controlled by the angleθc=arctan(4yb/c),which is a monotonically decreasing function ofcfor positive 4yb/c. As the tensile strain alongcaxis is increased,the degree of corrugation decreases,resulting in the formation of one-dimensional atomic chain alongcaxis. This atomic chain would affect the pre-exist atomic chain alongaaxis(see Fig.1)where the CDW transition intoα1-U occurs. The spacing of the new and pre-exist atomic chains is the first and the second nearest-neighbor distances, respectively. This shorter interatomic distance means that the formation of atomic chain alongcaxis yields the decrease of the tendency of CDW transition alongaaxis. Therefore, the tensile strain alongcaxis makes the CDW unstable and the compressive strain alongcaxis stabilizes the CDW phases.

Another perspective of atomic structure could be obtained from the variation of experimental lattice constants inα-U at low temperature.[11,12]As the temperature is decreased, the lattice constantsaandbfirst decrease to a minimum at 43 K and then rapidly increase whilecdecreases more rapidly below this temperature. That is to say,the cell dimensionsaandbshould expand andcshould contract for the stabilization of CDW order. This experimental observation is in agreement with our theoretical evaluation of strain effect on the CDW order.

Figure 3 also indicates that one can use the strain to effectively tune the CDW order. A very small strain, such as 0.5% tensile strain alongaaxis, would double the CDW formation energy and is very likely to increase the transition temperatureTCDW. This magnitude of strain is easily accessible in the experiment through the lattice mismatch between the substrate and the uranium film.[21]Compared to the layered transition-metal chalcogenide such as 1T-TiSe2,[24]the magnitude of strain to take effect is much smaller,which illustrates the sensitivity of 5f electrons. This sensitivity could be attributed to the narrow 5f bands that are actively bonding in the uranium.[51]

The effect of strain on the CDW order could also be viewed from the perspective of electronic structure. Let us go back to the topological change of Fermi surface aroundUpoint in Fig.A1. When comparing the Fermi surfaces ofα-U andα1-U,one can find that an ellipsoid object disappears due to the CDW distortion. It is equivalent to the band splitting at the Fermi level at the correspondingkpoints, i.e., Peierls distortion. The smaller the ellipsoid object is, the easier the Peierls distortion occurs. In Fig. 5, we plot the Fermi surfaces ofα-U when the tensile and compressive strains alongaandcaxes are applied. Clearly, the ellipsoid object is very small for the tensile strain alongaaxis and compressive strain alongcaxis. On the contrary, this object becomes larger for the compressive strain alongaaxis and tensile strain alongcaxis. To clarify this, the band structures corresponding to the Fermi surfaces in Fig. 5 are plotted in Fig. A3 (see Appendix A). One can find that the Dirac cone is closer to the Fermi level for the tensile strain alongaaxis and compressive strain alongcaxis, which means that the splitting is easier in these cases. These electronic structure calculations reconfirm that the effect of strain alongcaxis on the CDW order inα-U is abnormal.

Furthermore, the energetical instability usually indicates an intrinsic soft mode inα-U, i.e., the dynamical instability that drives the formation of the CDW transition.[17]Theαphase of uranium (see Figs. 1 and 4) is unstable at zero temperature,as demonstrated by the results in Fig.6(black solid line). Our calculation is consistent with the experimental data at room temperature.[4]From the other calculations in Fig.6,α-U is even more stable for the compressive strain alongaaxis and tensile strain alongcaxis. In particular,α-U is dynamically stable for a compressive strain of-0.5%,which is in agreement with the previous theoretical computation.[21]In contrast,α-U is even more unstable for the tensile strain alongaaxis and compressive strain alongcaxis. Overall,our argument about the abnormal effect of strain alongcaxis is also supported by the phonon calculations.

4. Conclusion

In summary, we investigate the effect of the uniaxial strain on the charge density wave(CDW)order inα-U within the framework of relativistic density-functional theory. When the strains alonga,b, andcare applied, the total energy,Fermi surface, and phonon mode are compared between theα-U structure with and without CDW distortion. From the calculation of the total energy difference, it is found that the tensile strain alonga/baxis increases the CDW instability and makesα-U even more unstable. The compressive strain alonga/baxis takes the opposite effect. This is very similar to the effect of pressure,in agreement with the previous literature,and intuitive. On the contrary,the effect of strain alongcaxis is counter-intuitive, in which the compressive/tensile strain increases/decreases the energetical instability ofα-U.This could be understood from the perspective of atomic,electronic, and phonon structures. From the atomic structure ofα-U, the increase of cell dimensioncmeans the emergence of a new one-dimensional atomic chain which is the rival of previous one-dimensional atomic chain for CDW distortion.The calculated Fermi surfaces and phonon modes for different strain also present the abnormal effect of strain alongcaxis with respect to that of strain alonga/baxis.

It is noteworthy that only the first CDW transition inα-U is considered here.Apparently,the strain would take effects on the other two CDW transitions. But the supercell for the structures with more CDW transitions is too huge and unreachable for modern supercomputer. In addition, the biaxial, triaxial,and more complex strains should take place in the experiment and the researches would be pursued in the near future.

Acknowledgements

The work was supported by the National Natural Science Foundation of China(Grant Nos. 22176181, 11874306,and 12174320), the Foundation of Science and Technology on Surface Physics and Chemistry Laboratory (Grant No. WDZC202101), and the Natural Science Foundation of Chongqing,China(Grant No. cstc2021jcyj-msxmX0209).

Appendix A

In this appendix, the supporting materials are provided.In Fig. A1, the Fermi surface ofα-U with and without distortion is presented. Our calculation is compared with that from the literature and the agreement is good. In particular,the topological change around theUpoint is very clear. The band structures corresponding to Figs.A1 and 5 are presented in Figs. A2 and A3, respectively. From the band structures,the band splitting of Peierls distortion is visible.

For an evaluation of PAW scheme, the CDW formation energy and distortion magnitude are also calculated using VASP and shown in Fig.A4. The Fermi surface ofα-U with different strains is presented in Fig.A5.The results from PAW calculations are in agreement with those from LAPW calculations.