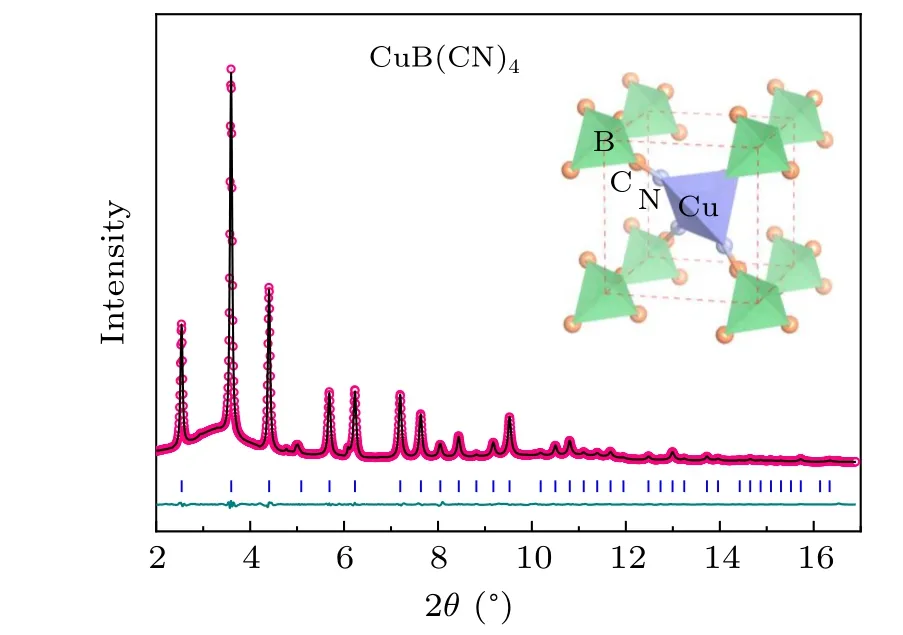
Isotropic negative thermal expansion and its mechanism in tetracyanidoborate salt CuB(CN)4

Chunyan Wang(王春艳) Qilong Gao(高其龙) Andrea Sanson and Yu Jia(贾瑜)

1Key Laboratory of Materials Physics of Ministry of Education,International Laboratory for Quantum Functional Materials of Henan,and School of Physics and Microelectronics,Zhengzhou University,Zhengzhou 450052,China

2Key Laboratory of Special Functional Materials of Ministry of Education,and School of Materials Science and Engineering,Henan University,Kaifeng 475004,China

3Key Laboratory for Quantum Materials and Center for Topological Functional Materials,Henan University,Kaifeng 475004,China

4Department of Physics and Astronomy,University of Padova,Padova I-35131,Italy

Keywords: negative thermal expansion,Prussian blue analogues,crystal structure,phonons

After the discovery that ZrW2O8displays strong negative thermal expansion (NTE) over a wide temperature range,[1,2]the interest in NTE has increased considerably due to its promising applications in different engineering fields from fiber optics coatings, high performance fuel cell cathodes to tooth fillings.[3,4]Since then different NTE materials were found out[5–8]and classified into two classes according to the NTE mechanism:[9–13]phonons driven open-framework materials, such as oxides,[1,3,14,15]fluorides,[16,17]cyanides/Prussian blue analogues (PBAs)[18–21]and MOFs;[22,23]electronic-related driven materials,such as magnetovolume effect in manganese nitrides[24,25]and Invar alloys,[26,27]ferroelectrovolume effect in PbTiO3,[28]charge transfer in BiNiO3,[29]metal–insulating transition in Ca2RuO4.[30]Other examples can be found in the review papers.[5,7,31,32]

The isotropic NTE materials are very interesting since they can reduce the thermal stress in composites,but,unfortunately,their number is very limited. ZrW2O8and ScF3are the most popular isotropic NTE materials. Their structural flexibility, directly connected to the transverse thermal vibrations of bridging atoms,plays a key role in NTE behavior.[33,34]Interestingly, Sanson[6]related the behavior of the transverse thermal vibrations and therefore of thermal expansion to the length of the crystallographic lattice parameter. Recently,Gaoet al.[35]adopted the concept of “average atomic volume(AAV)”to evaluate the structural flexibility and to qualitatively predict the thermal expansion behavior. Based on these ideas, some new negative and zero thermal expansion materials[36,37]were found out,including the CuB(CN)4NTE material presented in this work.

NTE in open-framework materials is typically related to the presence of low-frequency phonons with negative Gr¨uneisen parameters, but intriguing differences, based on their structural features, characterize each material and some aspects remain controversial. This is the case, for example,of zirconium tungstate ZrW2O8, where the origin of NTE has been widely debated in the years,[28,38]or the case ofMII(CN)2(M=Zn, Cd) cyanides, where two dominant optical modes seem to contribute mainly to NTE,[39]in contrast to other studies where NTE is attributed to transverse acoustic modes.[40]The isotropic NTE behavior of cubic CuB(CN)4was recently reported in Ref. [30], but no information is known about the origin of NTE. From the structure analysis reported in 2005 by Togoet al.,[41]the AAV of CuB(CN)4is close to the value 16 °A3, which is the critical point from positive to negative thermal expansion reported in Ref. [30]. CuB(CN)4is isostructural with AgB(CN)4and belongs to the Zn(CN)2-type structure. The C and N atoms in CuB(CN)4form linear B–C≡N–Cu linkages, a suitable condition that favors the NTE mechanism. In this work,we aim to shed light on the isotropic NTE mechanism observed in CuB(CN)4through a joint study of high-resolution synchrotron x-ray diffraction(SXRD),temperature-dependent Raman spectroscopy and first principles calculations based on density functional theory.

The crystal structure of CuB(CN)4was investigated by high-resolution SXRD (the detailed sample characterizations in supporting information) and the refined structure indicates that CuB(CN)4has a cubic structure with space groupP-43m(215) and lattice parametera= 5.40555(8) °A at 300 K, in agreement with a previous study.[36]Similar to AgB(CN)4,the CuB(CN)4structure is formed by CuN4and BC4tetrahedra,bridged through CN units(Fig.1). The value of the AAV for CuB(CN)4,calculated by equation AAV=V/(Z×N)whereVis the unit cell volume(V=157.95 °A3),Z is the cell formula units(Z=1)andNis the number of atoms in the chemical formula(N=10),is estimated to be about 15.8 °A3,hence close to the critical point for the switch from negative to positive thermal expansion.[30]

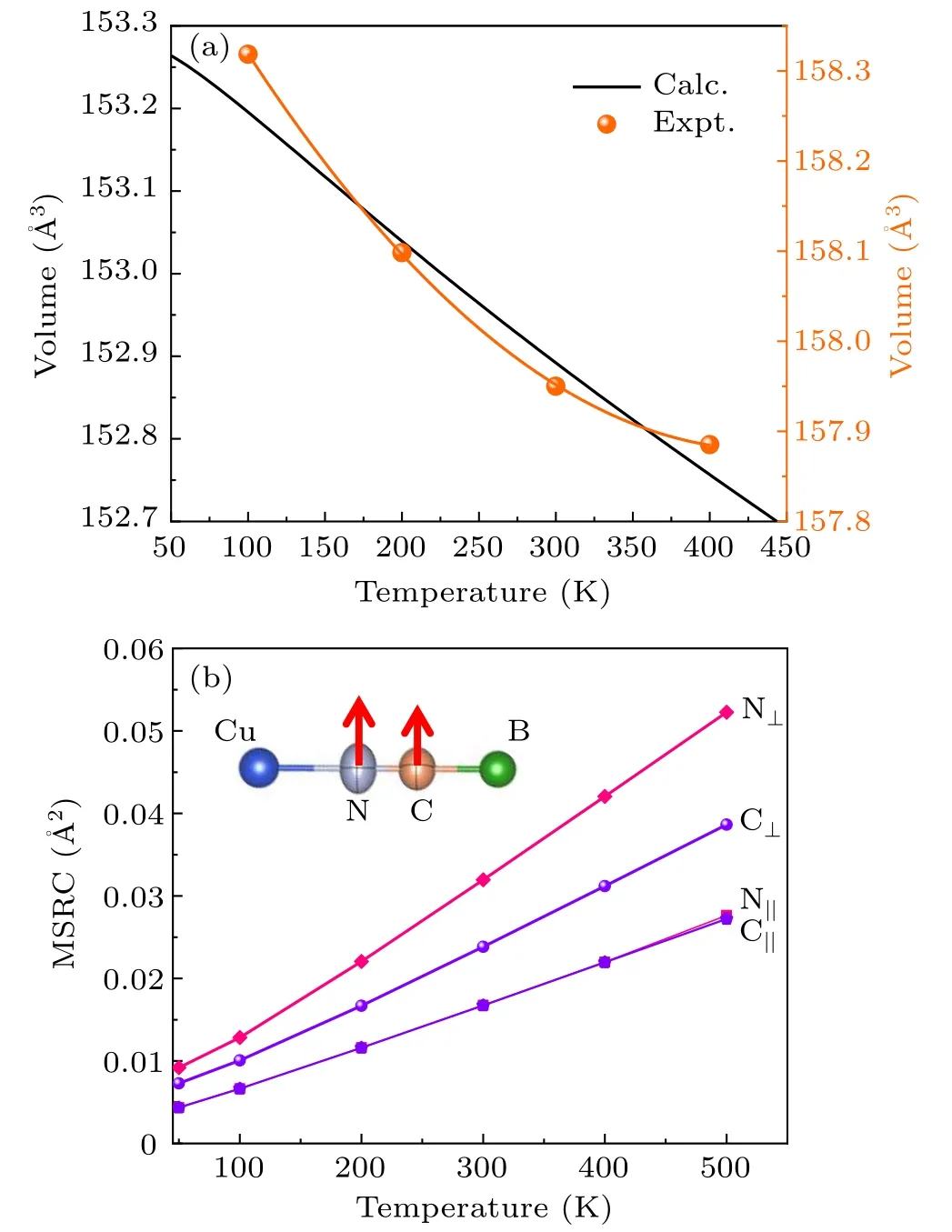
The thermal expansion of CuB(CN)4was determined by temperature-dependent SXRD.Interestingly,it displays an isotropic NTE behavior with linear thermal expansion coefficientαl=-9.15×10-6K-1in the temperature range 100–400 K. This experimental result is consistent with our DFT calculations,as shown in Fig.2(a). It can be observed that the NTE of CuB(CN)4is much weaker than that of isostructural AgB(CN)4(-40×10-6K-1,100–600 K),in agreement with the smaller value of the AAV.

It is widely accepted that the NTE in open-framework materials is driven by the transverse thermal vibrations of bridging atoms.[4]Here, the atomic mean-square displacements(MSDs)parallel(‖)and perpendicular(⊥)to the Cu–N≡C–B bond direction have been determined by SXRD analysis for the C and N atoms. As shown in Fig. 2(b), the perpendicular MSDs⊥of both N and C atoms are much larger than the parallel MSDs‖ones, thus indicating the presence of large anisotropy.In particular,the perpendicular MSDs⊥of N atoms are larger than that of C atoms. This suggests that the NTE in CuB(CN)4mainly comes from the transverse thermal vibrations of N atoms, similarly to other NTE PBAs such as TiCo(CN)6[42]and YFe(CN)6.[10]

Additional information on the lattice dynamics and NTE mechanism can be obtained by temperature-dependent Raman spectroscopy combined with first-principles calculations. On the basis of the factor group analysis, 2A1+2E+2F1+5F2vibrational modes at theΓ-point of the Brillouin zone are expected,where the F1and F2modes are triple degenerate modes and the E modes are double degenerate modes. The E and A1modes are Raman active, whereas the F2modes are both infrared and Raman active and the remaining F1modes are inactive (silent). Accordingly, nine Raman active modes are expected in CuB(CN)4. Figure 3(a) shows the (unpolarized)Raman spectrum collected in CuB(CN)4at 300 K,Table 1 reports the calculated phonon frequencies at theΓ-point.

According to our first-principles calculations, the experimental Raman peaks at about 160 cm-1and 277 cm-1correspond to the symmetric and anti-symmetric rocking vibrations of N-BC4groups, respectively, while the Raman peaks at about 200 cm-1, 508 cm-1and 520 cm-1correspond to the in-plane bending of B–C≡N bonds. The Raman peaks at～572 cm-1and～951/958/989 cm-1refer to the symmetric and anti-symmetric stretching vibrations of B-C bonds,respectively,and,finally,the two Raman peaks at about 2300 cm-1can be attributed to the stretching vibrations of the C≡N bonds. We guess here that the presence of three Raman peaks at 951/958/989 cm-1,also observed in Ref.[36],is the result of the degeneracy removal of the F2(R,IR)mode calculated at～941 cm-1. This statement is corroborated by the IR bands observed at the same frequency position.[43]Analogous conclusion can be hypothesized for the weak Raman peak detected at～2209 cm-1, also visible in Ref. [36], since at the same position there is again an IR peak. A very small peak seems visible also at～2228 cm-1in the lowest-temperature spectra.

Table 1. Calculated and observed vibrational modes of CuB(CN)4 at the Γ-point. The quantity has been estimated from the temperature dependence of Raman spectra,while the Gr¨uneisen parameters γi have been determined from first-principles calculations.

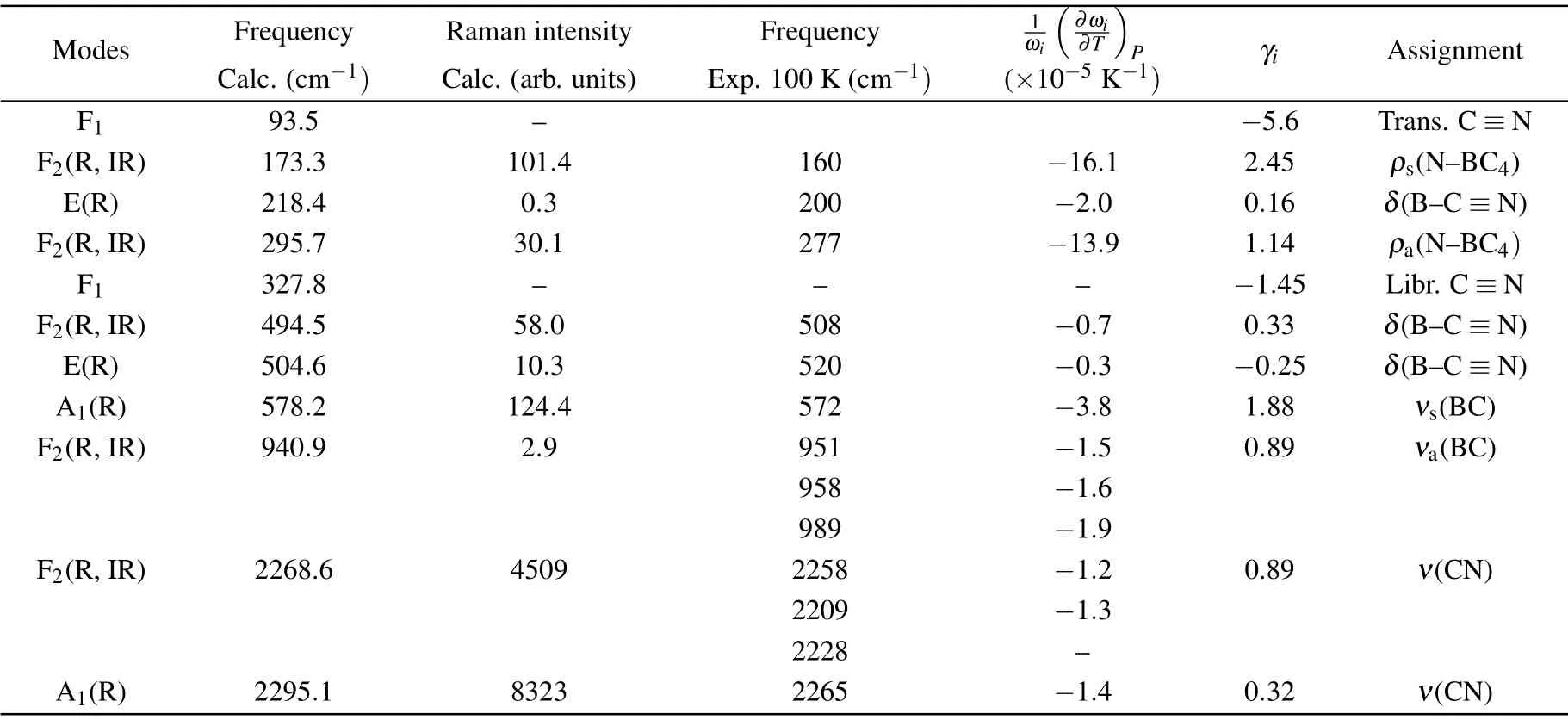
Table 1. Calculated and observed vibrational modes of CuB(CN)4 at the Γ-point. The quantity has been estimated from the temperature dependence of Raman spectra,while the Gr¨uneisen parameters γi have been determined from first-principles calculations.

Strengthened by the fact that our DFPT calculations reproduce satisfactorily the experimental Raman modes, both in frequency and intensity, we have calculated the phonon dispersion curves and the Gr¨uneisen parameters in the entire Brillouin zone to further investigate the NTE mechanism of CuB(CN)4(the detailed computational methods in supporting information). Figure 4(a)shows the phonon dispersion curves calculated along the high-symmetry directions of the Brillouin zone. No negative frequencies are observed, thus indicating that CuB(CN)4is dynamically stable. In the low-frequency region (＜300 cm-1), the projected density of states (PDOS)of CuB(CN)4is strongly related to the phonon vibrations of N atoms and,albeit to a lesser extent,to C and Cu atoms.

The modes Gr¨uneisen parameters atΓ(0 0 0) point is shown in Fig. 4(b). Due to the high symmetry of the space group, the number of phonon modes atΓ(0 0 0) point is much smaller. One can clearly observe that there are three phonon modes with negative Gr¨uneisen parameters: the lowest frequency phonon mode with the largest value of negative Gr¨uneisen parameters(90 cm-1,-5.6),is shown in the insert of Fig.4(b),which displays the same vibrations direction of N and C atoms; the second one is located at 337 cm-1with the opposite vibration directions of N and C atoms; the phonon mode at around 500 cm-1with small negative Gr¨uneisen parameter is corresponding toδBCNmode, it is consistent with results of temperature-dependent Raman spectra. Compared with the value of Gr¨uneisen parameters of the same and opposite transverse vibration direction of N and C atoms, it indicates that the NTE comes from the transverse vibration direction of N and C atoms,especially the same transverse vibration ones.

However, the number of phonon modes with negative Gr¨uneisen parameters atΓ(0 0 0) point is still smaller than that of phonon modes with positive Gr¨uneisen parameters.Figure 4(c) shows the mode Gr¨uneisen parameters along all the high-symmetry directions in BZ.One can observe that the acoustic modes atX(0.5 0 0)andM(0.5 0.5 0)besides optical mode atR(0.5 0.5 0.5) also have larger negative Gr¨uneisen parameters. It suggests that the acoustic modes also play a critical role in driving the NTE behavior, similarly found also in other materials such as Zn(CN)2,[40]Cu2O,[45]MOF-5[22]and Ni2W(CN)8.[46]The typical eigenvectors of vibrational modes with larger negative Gr¨uneisen parameters have been illustrated in Fig. 4(d). The vibrational mode with negative Gr¨uneisen parameters atRpoint is similar to that atΓpoint, while these atXandMare mainly the acoustic vibration of Cu atoms caused by the collective torsion of all atoms in CuB(CN)4.

In conclusion,CuB(CN)4displays isotropic NTE and the origin of its thermal expansion behavior has been investigated by SXRD,Raman spectroscopy and the first-principles calculations. The presence of large transverse thermal vibrations of C and N atoms is the driving force for NTE of CuB(CN)4,especially those of N atoms. The analysis of the vibrational modes reveals that both the acoustic and low-frequency optical phonon modes give the main contribution to NTE. This work shed light on the NTE mechanism of CuB(CN)4,a new isotropic NTE material.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos. 22071221, 21905252, and 11774078), Natural Science Foundation of Henan Province,China (Grant No. 212300410086), and Innovation Scientists and Technicians Troop Construction Projects of Henan Province, China (No. 10094100510025). All calculations were supported by National Supercomputing Center in Zhengzhou.