含电-气-热耦合系统的微电网频率安全评估

陈 哲，邓宝华，金建新，张有兵

（1.国网浙江省电力有限公司平阳县供电公司，温州 325000；2.浙江工业大学信息工程学院，杭州 310023；3.平阳县昌泰电力实业有限公司，温州 325400）

为解决传统用于发电的石油、煤炭等不可再生能源短缺、环境污染严重等问题，早日实现我国“碳达峰、碳中和”的战略目标[1-2]，亟需一种新形态下的能源供给系统。综合能源系统将各种不同属性的能源耦合在一起，可以进行各种能源之间的统筹优化，充分发挥不同属性能源的优势，提高系统整体的能源利用率[3]。然而随着各能源子系统之间耦合性的增强及设备种类的日益丰富，给综合能源系统的安全运行带来了巨大挑战。

以气系统为例，由于天然气发电具有高效、清洁等优势，近年来在电力系统中的占比不断攀升[4]。大规模天然气引入系统后，使电、气系统之间的耦合性增强的同时，也导致系统的可靠性问题日益凸显[5]。例如，天然气管道出现泄漏、气源供给中断等随机故障均可能导致燃气机组因天然气的供给不足，使出力迅速减小的情况发生，进而威胁到电系统的安全稳定运行[6]。此外，随着综合能源系统中热负荷需求的逐渐增大，一旦气系统中发生随机故障，燃气锅炉由于天然气供给不足，供热能力减弱，势必会增大电系统中电制热设备的投入，可能引起电系统中的供需不平衡，进而危及到系统频率的安全稳定。

此外，就电系统本身来说，其内部的常规发电机组正逐步被分布式能源替代。分布式能源通过电力电子装置接入电网，会造成整个系统的转动惯量水平降低[7]，从而导致系统的调频能力减弱。同时，随着可再生能源渗透率的不断提高，容易造成电源侧输出功率波动。而类似于电动汽车等储能电池因其具有较快的爬坡响应速率[8-9]，在出现电能供需不平衡时，可为系统提供备用电源支持，使系统的可靠性得到提高，实现对电能的削峰填谷[10]。但大量储能设备的接入也增加了系统的负荷，这些都是导致系统频率安全问题的主要原因[11-12]。

频率是电能质量评估的重要性指标[13]。目前电力系统频率主要通过时域仿真法[14]、解析法[15]和机器学习方法进行评估。然而，时域仿真法存在运算耗时长、计算复杂程度高等缺点，无法满足在线应用的要求。文献[15]利用解析法获得动态频率响应曲线，但忽略了系统阻尼系数、旋转备用等因素对动态频率响应的影响，不可避免地引入了误差。近年来迅速发展的机器学习方法虽然为电力系统的频率评估提供了新思路[16]，但仅仅是利用数据统计方法对历史数据信息进行挖掘分析[17-20]，使该方法的有效性受到样本选取方式、样本质量及本身算法差异的影响[21]。同时，由于脱离系统物理结构，这一方法应用于具有强因果关系的电力系统领域中时，得到结果的可靠性受到一些质疑。针对机器学习方法的不足，文献[22]提出一种基于物理模型与数据驱动模型的集成算法，但该方法中的数据驱动模型采用单层神经网络，对输入特征的学习能力有限。

本文充分考虑到可再生能源设备出力的不确定性、天然气网络中“气源不足”故障扰动产生的气电转换功率缺额、储能装置输出功率的变化情况，以及不同发电机组的出力特性、机组爬坡速率等运行约束，构建了一个预想天然气网络中“气源不足”故障扰动下微电网的动态频率响应模型，并采用基于解析模型与数据驱动模型的融合建模方法对预想天然气网络中“气源不足”故障扰动下的微电网频率性能进行综合评估。实验结果表明，相比于传统机器学习方法，本文中所提的融合建模方法的评估精度更高。

1 含多能源系统的微电网结构及其动态频率响应模型

典型含多能源系统的微电网结构如图1所示。由图1可知，该微网主要包含风机、储能元件、燃气锅炉及燃气轮机等，可以同时满足电、热、冷多种类型负荷的需求。

图1 含多能源系统的微电网结构Fig.1 Microgrid structure with multi-source system

在并网模式下，含多能源系统的微电网与上级电网相连。当微电网中发电设备的总输出电量无法满足系统自身用电需求时，系统通过上级电网进行购电；当其在满足电、热、冷各种负荷需求后，冗余电量也可以售电给上级电网，从而获取更高的收益。除此之外，系统中的电储能设备也可以参与电网的需求响应，实现电能的削峰填谷，提高系统的经济效益。

当上级电网出现停电故障时，微电网系统可以转换为孤岛模式。该模式是在脱离主网支持的情况下，为维持自身区域性电网稳定而切换的运行模式[23]。在孤岛模式下，系统无法从上级电网购电，由系统内部各种发电设备一起供电。

然而随着微电网中多能源子系统的耦合程度越来越高，系统内随机故障的发生对系统频率的安全稳定产生了巨大的威胁。以电、气耦合系统为例，当天然气供应不足或燃气轮机发生跳闸事故时，不仅会导致电网络的供电量不足，威胁到电网络的安全稳定运行，还会导致热量的损失，满足不了热负荷的需求。而气网络中气源不足导致的热损失，也会影响到电网络，电网络需要提供气网络部分热负荷的电能，从而使电网络中的电负荷增大。因此，含多能源系统的微电网内部子系统都是紧密耦合的，在评估微电网频率的性能指标时需要综合考虑其他能源子系统对其产生的影响。

本文针对含电-气-热耦合系统的微电网，构建该微网的动态频率响应模型，并利用基于解析模型与数据驱动模型的融合建模方法对其频率性能指标进行综合评估。微电网的动态频率响应模型如图2所示，由图2可知，该模型主要由不同类型的发电机组、电动汽车集群、风电功率Pwind，以及气电转换功率缺额等组成。其中，Ri为任意调速器i的调差系数；Δf、J和D分别为频率偏差、系统等效惯性常数和负荷阻尼系数；分别为调速器和发电机组i的时间常数；TPEV为电动汽车模型的时间常数；δi、Li分别为发电机组i的爬坡速率和旋转备用容量；分别为发电机i的输出功率和电动汽车集群等效模型的输出功率；KPEV、CPEV分别为电动汽车的参与因子和电动汽车的数量；s为频域的表现形式。

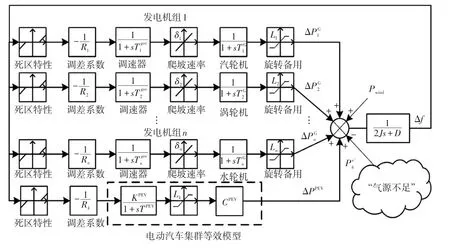
图2 微电网的动态频率响应模型Fig.2 Dynamic frequency response model of microgrid

2 基于解析模型与数据驱动模型的融合建模方法

在本文所提的融合建模方法中，首先，利用解析模型对电力系统中的因果关系进行数学意义上的描述，获得相应特征的映射关系，进而保留电力系统物理结构信息，通过解析模型所获得的评估结果可以为机器学习方法提供理论指导。然后，将解析模型得到的评估结果与离线仿真获得的历史数据库中的输出样本之间的误差数据信息和系统运行状态信息进行重构。最后，把重构数据和历史数据库中的输出样本分别作为数据驱动模型的输入样本和输出样本，并对其进行训练。该融合建模方法在利用解析模型较好地实现系统物理结构描述的同时，还具有利用数据驱动模型快速挖掘数据信息，以及对重构数据中的误差数据信息进行校正的能力，进而保证了该方法的可靠性与精确性。

2.1 电气热耦合系统

2.1.1 燃气轮机

燃气轮机是电气热耦合系统中重要的能量输出设备，它可以利用天然气燃烧释放的高温热能进行发电，发电后的余热经过回收利用还可以满足热负荷的需求。该设备输出的电功率及回收的热功率可表示为

2.1.2 燃气锅炉

除了燃气轮机回收的热量，燃气锅炉燃烧天然气也可以提供大量的热能，其输出的热功率为

由于本文在考虑电气热耦合系统中的耦合特性时主要是针对天然气网络中“气源不足”故障扰动的情况，因此在对微电网的频率性能进行评估时还需考虑气电耦合时因“气源不足”故障扰动产生的气电转换功率缺额的影响。针对天然气网络中“气源不足”故障扰动产生的气电转换功率缺额、风电功率Pwind，以及电动汽车集群等效模型输出功率ΔPPEV的微电网的动态频率响应模型，本文提出一种利用解析模型与数据驱动模型融合建模的方法用于其频率性能的评估。

2.2 解析模型

由于式（7）～（9）在进行频率性能指标评估的过程中忽略了负荷阻尼系数、机组旋转备用水平及非线性的爬坡过程等因素，只能得到一个粗略的评估结果，不可避免会引入误差。如果要全面考虑各种因素的影响，虽然评估精度会有所提高，但解析模型会变得更加复杂。

本文充分考虑解析模型评估精度和模型复杂程度之间的矛盾，将机器学习方法作为误差校正模型，用于校正解析模型产生的评估误差。

2.3 数据驱动模型

在本文所提的融合建模方法中，数据驱动模型采用的是基于降噪自动编码器的深度极限学习机ELM（extreme learning machine）这一机器学习方法，并将其作为误差校正模型用于校正解析模型在忽略部分环节时导致的误差。ELM本质上是一种单隐含层前馈神经网络[25]，因其具有训练时间短、分析计算效率高等优点，逐渐被应用于各种领域。然而随着实际问题的复杂化，单层神经网络架构的ELM已经不能满足现实需要。文献[26]将自动编码器与ELM算法结合，得到一种基于ELM-自动编码器ELM-AE（ELM autoencoder）算法的多层极限学习机。通过增加网络深度，提高了数据驱动模型的学习能力，使一些复杂问题的解决成为可能。然而受网络模型复杂度、训练数据集和数据噪音等因素影响，利用自动编码器得到的初始网络模型往往存在过拟合的风险。本文利用“腐蚀”样本的方式对ELM-AE算法中自动编码器作了进一步改进，得到一种ELM-降噪自动编码器ELM-DAE（ELM denois⁃ing autoencoder）算法。其中，降噪自动编码器的网络框架如图3所示。

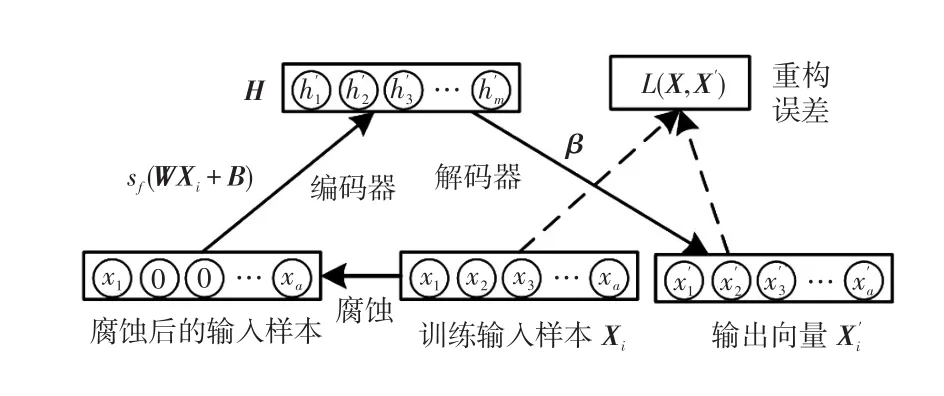
图3 降噪自动编码器的网络框架Fig.3 Network framework of denoising autoencoder

基于ELM-DAE算法的深度ELM网络框架如图4所示。由图4可知，首先，利用降噪自动编码器获得式（12）中的重构误差，并利用式（13）、（14）更新网络权重W和阈值B，实现重构误差的最小化。然后，根据ELM-DAE算法原理，以第k层隐含层的特征向量Hk为输入，利用式（15）求解第k+1层隐含层的输入权重矩阵βk+1，并将βTk+1作为原网络中隐含层hk与hk+1之间的权重矩阵。最后，通过式（16）近似求解出β′。

图4 基于ELM-DAE算法的深度ELM网络Fig.4 Deep extreme learning machine network based on ELM-DAE algorithm

基于ELM-DAE算法的深度ELM模型可以有效解决网络参数W和B随机生成带来的问题，在提取更深层次的关键特征信息的同时，降低了模型过拟合的风险。

3 基于融合建模方法的频率性能指标评估流程

基于融合建模方法的频率性能指标评估流程如图5所示。

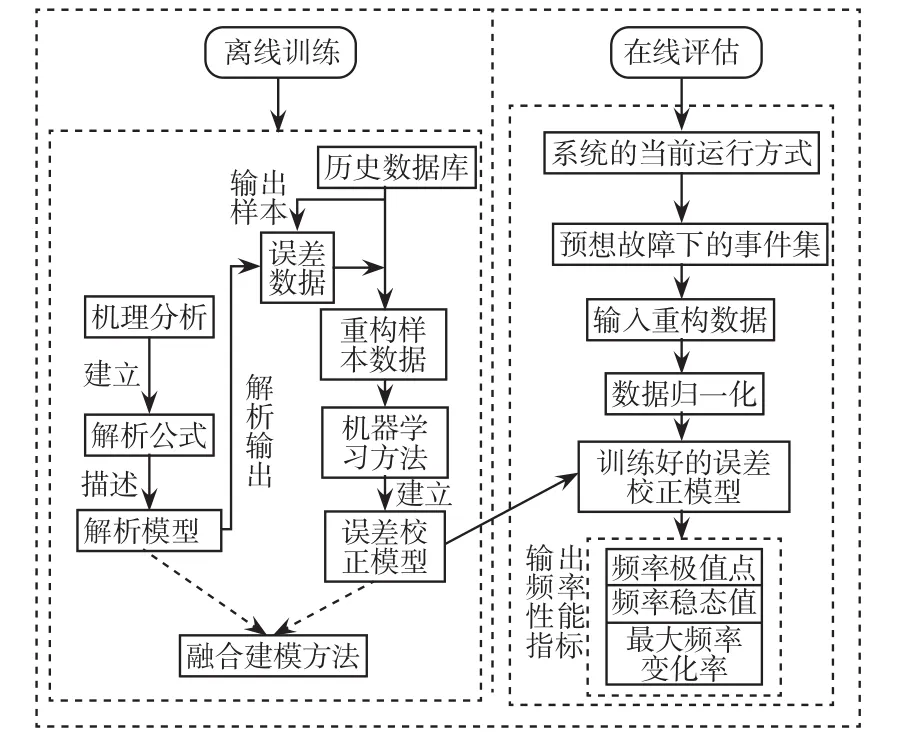
图5 基于融合建模方法的频率性能指标评估流程Fig.5 Flow chart of evaluation of frequency performance index based on fusion modeling method

3.1 离线训练

误差校正模型的离线训练流程如图6所示，其步骤如下。

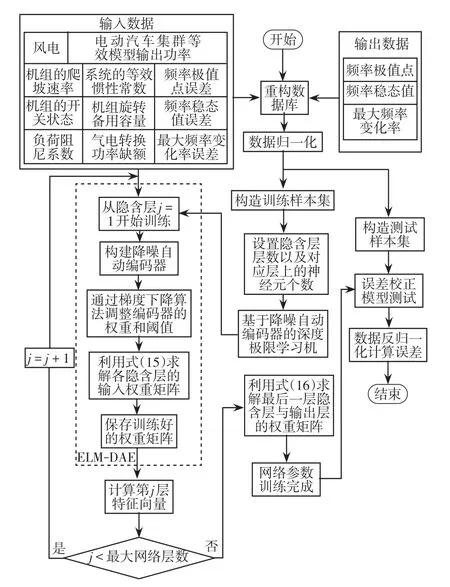
图6 离线训练流程Fig.6 Flow chart of offline training

步骤1兼顾离线时域仿真数据和解析公式的输入、输出数据，得到用于训练误差校正模型的样本数据库。

步骤2对样本数据库中的输入、输出数据进行归一化处理，并将样本数据分为训练集和测试集。

步骤3对基于降噪自动编码器的深度极限学习机网络参数（隐含层层数、各隐含层的神经元个数）进行设置。

步骤4利用ELM-DAE算法，求解网络中的输入权重矩阵和输出权重矩阵。

将平均绝对百分比误差MAPE（mean absolute percentage error）作为衡量传统机器学习方法与融合建模方法的评估性能标准，MAPE可表示为

3.2 在线评估

在线评估流程的步骤如下：

步骤1制定预想天然气网络中“气源不足”故障扰动下的事件集；

步骤2形成输入数据，并对输入数据进行归一化处理；

步骤3将步骤2得到的数据输入到已离线训练好的误差校正模型中，获得输出数据；

步骤4将步骤3得到的输出数据进行反归一化处理，得到预想天然气网络中“气源不足”故障扰动下频率的3个性能指标（频率极值点、频率稳态值、最大频率变化率），并依据该结果对微电网的频率性能进行综合评判。

4 算例分析

为了验证融合建模方法评估系统频率的可行性，利用MATLAB软件实现算法编写，计算机配置为CPUIntel Core i5、内存8GB。

4.1 样本数据集的构造

利用SIMULINK平台搭建图2中微电网的动态频率响应模型。该模型含有包括燃气轮机在内的8台发电机和1个电动汽车集群，以及风机发电设备。负荷的基准值为150 MW，系统的额定频率为50 Hz。典型某时段内天然气的热值λgas=1×10-2MW/m3，燃气消耗速率最大值为400 m3/h，燃气轮机的发电效率。为了考虑可再生能源、储能设备及天然气网络中“气源不足”故障扰动产生的气电转换功率缺额对微电网频率性能指标的影响，微电网动态频率响应模型中的按照式（1）和式（4）计算典型某时段内气电转换功率缺额的最大值，其中k=0.8；电动汽车集群等效模型最大、最小的输出功率分别为1 MW和0 MW；风电出力的波动变化范围为[-2MW，+2MW]。由于综合考虑了微电网中风电出力，以及电动汽车集群等效模型输出功率的波动变化情况、不同水平下的气电转换功率缺额、各台发电机组的开关状态、爬坡速率和旋转备用容量等因素，导致模型经离线仿真后得到的数据集较大，总计36 000组样本数据。

与此同时，通过解析模型获得能表征系统因果关系的36 000组样本数据。将解析模型获得的数据中的输出样本与离线仿真得到的样本数据进行重构，获得36 000组的重构样本数据，并随机选取其中30 000组数据作为误差校正模型的训练样本集，剩余6 000组数据作为测试样本集。

4.2 输入特征选取

误差校正模型在传统机器学习方法的基础上增加了3个特征输入（频率极值点误差、频率稳态值误差和最大频率变化率误差），模型的输入变量组成与个数如表1所示。

表1 输入变量组成与个数Tab.1 Composition and number of input variables

4.3 误差校正模型的网络架构

图7分别给出了传统机器学习方法与融合建模方法下基于ELM-DAE算法的深度ELM模型在不同网络参数下的MAPE值。由于深度ELM的隐含层层数，以及各隐含层上的神经元个数都会对系统频率的安全性能评估精度产生一定的影响，因此需要对这些网络参数进行合理设置，进而保证系统频率性能指标的评估精度。

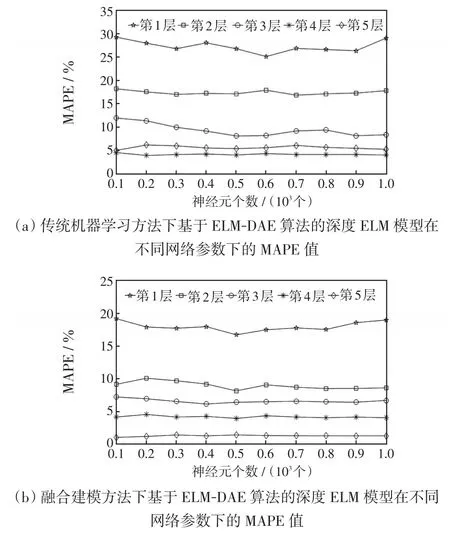
图7 不同网络参数下的MAPEFig.7 MAPE under different network parameters

由图7可知，对于该算例系统，传统机器学习方法与融合建模方法下网络的最佳隐含层层数分别为4层和5层，其中传统机器学习方法下各个隐含层上神经元最佳个数分别为600、700、500、200、100，而融合建模方法下各个隐含层上神经元最佳个数分别为 500、500、400、300、100；在同等的MAPE值下，融合建模方法中的误差校正模型相比于传统机器学习方法中的神经网络架构更为简单，所需的隐含层数较少，并且融合建模方法中误差校正模型在同等网络参数下的MAPE都要低于传统机器学习方法。

4.4 结果分析与对比

基于第4.3节分析，可以分别建立传统机器学习方法与融合建模方法下神经网络模型的最佳网络架构，并根据该网络架构对训练样本进行离线深度学习，从而分别得到训练好的系统频率性能指标评估模型。表2和表3分别给出了时域仿真和传统机器学习方法、融合建模方法在6 000组测试样本下的评估结果。

表2 时域仿真和传统机器学习方法的评估结果Tab.2 Evaluation results of time-domain simulation and traditional machine learning methods

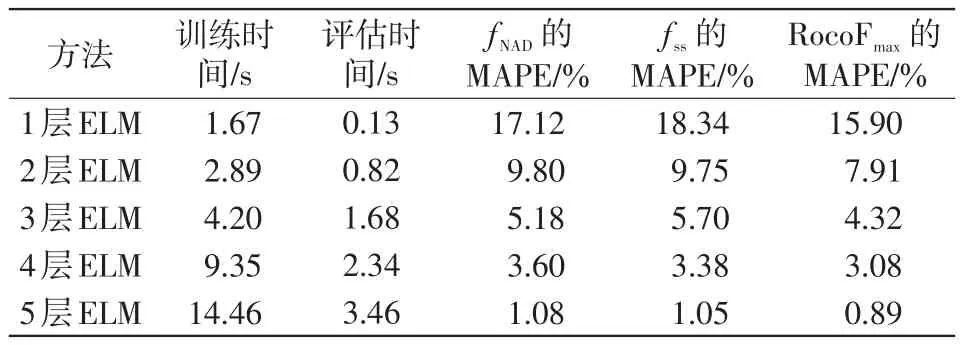
表3 融合建模方法中误差校正模型的评估结果Tab.3 Evaluation results of error correction model in fusion modeling method

为了得到6 000组预想天然气网络中“气源不足”故障扰动下的3个频率性能指标，采用时域仿真方法需要重复执行6 000次的仿真实验，实验仿真总时长耗费将近635.19 s。由此可见，对于该算例系统，考虑发电机组的出力特性、可再生能源发电波动、电动汽车集群等效模型输出功率变化，以及天然气网络中“气源不足”故障扰动后，时域仿真方法下的运算效率太低，已经不能满足实际应用。而且实际系统的运行方式更为复杂，各种不确定因素将使预想故障扰动事件的数据集相当可观，时域仿真的方法已经不再适用。

在表2和表3中，传统机器学习方法与融合建模方法下网络的隐含层总数设置为5层，并依次将这5个隐含层上神经元的个数设置为600、700、500、200、100和500、500、400、300、100。从表2、表3中可以看出，不管是针对传统机器学习方法还是融合建模方法，多隐含层的网络架构相较于浅层网络架构都有着明显的优势。随着隐含层数量的逐渐累加，传统机器学习方法与融合建模方法下网络的离线训练时间也会逐渐增加，当隐含层数量为5层时，两者的离线训练时间分别为13.24 s和14.46 s，且两者在线评估时间都在3 s左右。相比于时域仿真方法，上述两种方法对系统的频率性能评估时间都大大缩短，满足了系统频率性能指标的在线评估要求。

由表2可以看出，随着隐含层数目的增加，传统机器学习方法下基于ELM-DAE算法的深度ELM离线训练时间由1.10 s逐层增加至13.24 s，系统频率性能指标的在线评估时间由0.08 s增至2.56 s；多隐含层的网络架构评估精度一般都高于单隐含层，但隐含层层数也不是越多越好，需要合理选取隐含层和对应神经元的数量。当隐含层为4层时，基于ELM-DAE算法的深度ELM已经达到较高的精度，频率极值点fNAD、频率稳态值fss、最大频率变化率RocoFmax3个频率性能指标的MAPE仅为4.94%、4.75%、4.03%。

相较于表2，表3中误差校正模型充分考虑了解析模型的输出结果和实际数据信息，在模型的特征输入中引入了3个频率性能指标误差，进一步提高了模型的评估精度。在同等隐含层的条件下，表3中的误差校正模型评估精度都要高于表2；当误差校正模型的隐含层为5层时，已经具有极高的精度，3个频率性能指标的MAPE值明显低于表2；此外，表3中误差校正模型的离线训练和在线评估时间相较于表2，几乎没有增加。由此可见，基于融合建模方法的误差校正模型的频率性能指标评估性能要好于传统机器学习方法。

为进一步验证融合建模方法的有效性，通过改变风电出力，以及电动汽车集群等效模型输出功率的波动范围、不同水平下的气电转换功率缺额、各台发电机组的开关状态、爬坡速率和旋转备用容量等因素，重新生成2 000组新的测试样本。在传统机器学习方法与融合建模方法下，基于ELM-DAE算法的深度ELM网络参数都取最优时，利用新的测试样本对两者的泛化能力进行分析比较，所得的频率性能指标（频率极值点、频率稳态值、最大频率变化率）的误差分布对比如图8所示。其中，图8（a）、（b）、（c）分别表示频率极值点、频率稳态值、最大频率变化率3个频率性能指标在传统机器学习方法和融合建模方法下误差分布对比情况。

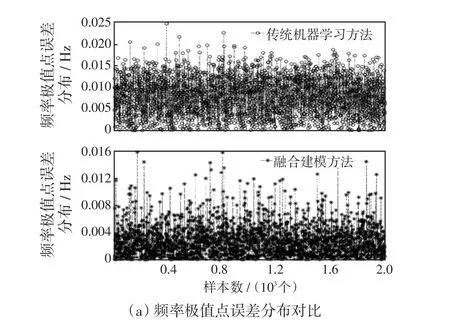
图8 频率性能指标的误差分布对比Fig.8 Comparison of error distribution of frequency performance indexes

由图8可以看出，当两种方法下的网络参数达到最优时，传统机器学习方法下基于ELM-DAE算法的深度ELM所得的频率极值点、频率稳态值、最大频率变化率3者的误差主要集中分布在0～0.025 Hz、0～0.023 Hz、0～0.018 Hz/s的范围内，而经过“先解析，后校正”的融合建模方法下基于ELM-DAE算法的深度ELM所得频率极值点、频率稳态值、最大频率变化率3者的误差均远小于前者，主要分布在0～0.005 Hz的范围内，与实际值非常接近。综上所述，相比于传统机器学习方法，融合建模方法有助于提高系统频率的性能评估精度，并在实际应用过程中利用解析模型保留了电力系统中的物理结构信息，保证了评估结果的可靠性。

5 结语

本文以含电-气-热耦合系统的微电网为研究对象，综合考虑到综合能源系统中的耦合特性、电动汽车，以及可再生能源发电特性等因素对微电网频率稳定造成的影响，提出一种基于解析模型与数据驱动模型的融合建模方法，用于评估电网络的频率性能指标。基于解析模型与数据驱动模型的融合建模方法在利用解析模型保留电力系统因果关系的同时，将基于ELM-DAE作为误差校正模型用于校正解析模型忽略部分环节造成的误差。相比于传统机器学习方法，该融合建模方法不仅确保了含电-气-热耦合系统中微电网的频率性能指标评估结果的可靠性，也进一步提高了评估精度。