基于MOGWO的拟人机械手连杆长度优化*

潘楚光，谭 平，熊瑞平，杨 康

(四川大学机械工程学院，成都 610065)

0 引言

拟人机械手作为一种模拟人类手臂运动机制的仿生机构具有与人类手臂类似的优点[1]。然而，受工作环境和机械结构的限制，拟人机械手的总长度往往受到一定程度的限制，这极大影响其运动性能[2]。在满足约束的前提下，通过优化拟人机械手的连杆长度来提高运动性能已成为拟人机械手设计的重要工作。

为了更好地模拟人体手臂的操作，拟人机械手既要具备良好的灵活性，又要保证机械手末端具有较高的精度。因此，拟人机械手的灵活性/可操作性和端部刚度性能成为优化连杆长度参数的主要参考[3]。为了提升拟人机械手的灵活性，贾世元等[4]提出使用可操作性作为连杆长度参数的评价指标，研究了机械手的尺寸优化方法。刘亚军等[5]揭示了机械臂可达工作空间随结构尺度参数和关节运动范围的变化规律，综合得出一组最优的机械臂结构尺度参数。刘海涛等[6]基于工作空间、奇异性、各向同性等性能评价指标优化机械臂连杆长度参数。陈世钟等[7]基于静态刚度模型，分析了如何通过优化机械手的长度和配置来提高刚度。提出了一个全局刚度性能指标，并将其用作优化机械手连杆长度的目标函数。焦嘉琛等[8]基于静态刚度模型设计了六自由度串联机器人的综合刚度性能评价指标。陈伟海等[9]分析了绳驱动七自由度拟人机械手的笛卡尔刚度，并提出一种优化算法以提高机械手在运动过程中的刚度性能。

对于拟人机械臂的连杆长度参数优化设计问题，大多数研究仅从可操作性或刚度性能单方面展开。然而，仅以刚度性能指标作为评价指标来优化机械手的连杆长度，并不能保证机械手的可操作性[10]。因此，为了平衡拟人机械手的可操作性和刚度性能，本文综合考虑可操作性以及端部刚度性能建立多目标优化模型，利用MOGMO求解拟人机械手连杆长度参数的优化设计问题。

1 人体手臂的运动机制和配置分析

1.1 人体手臂运动机制

开发拟人机械手时需要对人体手臂的运动机制进行分析，以便更好地模拟人体手臂。在人体运动解剖学中，人体手臂自上而下由肩关节、上臂、肘关节、前臂和腕关节组成，其运动主要来自于关节的运动。人体手臂通常被简化为具有7个自由度的机构，包括肩关节的3个自由度、肘关节的1个自由度和腕关节的3个自由度[11]。

人体手臂的肩关节是典型的球窝关节，是人体最灵活的关节。其运动形式包括前屈后伸、外展内收、内旋外旋。肘关节是单自由度旋转关节，可实现人体手臂的屈曲和伸展。腕关节由桡关节和腕骨关节组成。由于两个关节可以相互独立运动，因此腕关节可以看作是由具有单自由度的环轴关节和具有两个自由度的髁关节组成。腕关节的运动形式包括伸屈、桡屈和尺屈、前后旋转。通过实际测量和数据分析，可以得到人体手臂的运动形式和相应的运动范围，如表1所示。

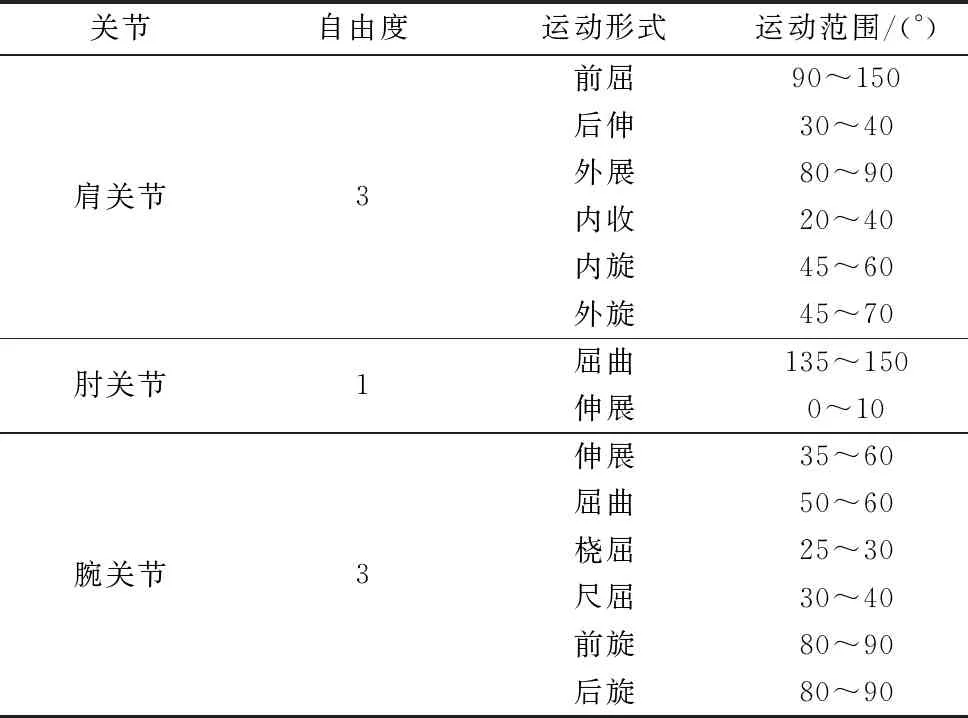
表1 人体手臂运动形式和运动范围

1.2 人体手臂的配置分析

开发拟人机械手的基本出发点是使其在工作环境中更具灵活性和适应性，从而实现与人类手臂类似的运动性能和工作空间。受机械结构的限制，难以完全复制人类手臂的结构。人体手臂的每个关节都可以等效为一个具有相同运动形式的机械运动副，然后可以根据具体的配置选择合理的设计方案。目前人体手臂大多采用7自由度配置，肩关节由3个串联的旋转关节组成，肘关节为1个旋转关节，腕关节与肩关节类似由3个串联旋转关节组成。

对于7自由度人体手臂结构，不同关节设置的拟人机械手具有不同的配置，如图1所示的配置被认为是最佳的。与广泛使用的6自由度机械手配置相比，该配置在关节2和关节4之间沿两条平行轴的公共法线方向增加了一个旋转关节3。

图1 最佳的拟人机械手配置

2 拟人机械手的性能评价指标

具有7自由度的拟人机械手不仅可以消除工作空间中的奇异构型，还可以灵活避开关节限制和空间障碍，实现人体手臂的操作姿态和功能。在确定配置后，根据具体的任务需求优化机械手的连杆长度参数是拟人机械手设计过程中的关键步骤。本文主要依据可操作性和端部刚性性能指标对拟人机械手的连杆长度参数进行优化设计。

2.1 拟人机械手的正运动学

对于图1所示的拟人机械手的配置，连杆长度分别为l1、l2、l3、l4、l5、l6、l7，如图2所示。

图2 拟人机械手的连杆参数

图中，d1=l1+l2；d2=l3+l4；d3=l5+l6；d4=l7。

利用螺旋理论建立拟人机械手的运动学模型。首先，建立基坐标系Os-XsYsZs以及末端坐标系Ot-XtYtZt，如图3所示。其中ωi是关节i旋转轴的单位向量。

图3 拟人机械手的螺旋坐标

机械手初始姿态的齐次变换矩阵为：

(1)

关节i对应的旋转轴单位向量ωi=(ωix,ωiy,ωiz)T以及位置向量pi=(pix,piy,piz)T，因此对应的运动螺旋坐标ξi为：

(2)

每个关节的单位旋转轴向量ωi和位置向量pi如表2所示。

表2 拟人机械手关节轴向量与位置坐标

根据表2及式(2)可以得到每个关节的运动螺旋坐标ξi如表3所示。

表3 拟人机械手关节运动螺旋坐标

(3)

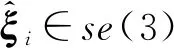
(4)

姿态矩阵的指数形式为：

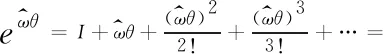
(5)

运动螺旋矩阵的指数形式为：

(6)

根据上述公式，可以得到每个关节的指数积。

因此拟人机械手的正向运动学为：

(7)

(8)

式中，

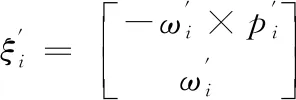
2.2 建立性能评价指标

由于雅可比矩阵J表示末端运动速度与关节运动速度之间的映射关系，因此雅可比矩阵的代数特征，如行列式、条件数、最大和最小奇异值等通常作为评价拟人机械手灵活性的性能指标。为了保证运动精度和动态性能，需要同时考虑机械手的刚度性能。

(2)静态刚度性能指标。在拟人机械手的设计过程中，端部刚度也是一个重要的性能评价指标。端部刚度取决于关节刚度矩阵和雅可比矩阵[13]。具有n个自由度机械手的关节i的刚度用Kqi(i=1,2,…,n)表示，关节刚度矩阵Kq表示为：

Kq=diag(Kq1,Kq2,…,Kqn)

(9)

拟人机械手的雅可比矩阵J∈R6×7，端部刚度矩阵K可以根据雅可比矩阵的广义逆J+被表示为：

K=(J+)KqJ+

(10)

代入J+=JT(JJT)-1到式(10)并化简得：

K=(JJT)-TJKqJT(JJT)-1

(11)

取刚度矩阵K的最小奇异值为σmin(K)。对于整个工作空间，机械手末端在奇异值最小的位置刚度最弱，拟人机械手末端的变形最大。因此，最小奇异值σmin(K)越大，对应的刚度越大。

为了衡量拟人机械手在整个工作空间的性能，可操作性指标和静态刚度性能指标分别在整个工作空间上积分，得到对应的全局性能指标。

(12)

(13)

式中，f1为可操作性的全局性能指标；f2为端部刚度性能的全局性能指标；W为拟人机械手的工作空间；ψ为关节运动空间；θi为拟人机械手的关节角。

3 拟人机械手的连杆长度参数优化

3.1 建立优化模型

机械手连杆长度参数优化是在机械手的长度约束范围内，寻找一组最优的连杆长度参数，在给定的优化性能指标下。拟人机械手的全局性能指标f1和f2为机械手连杆长度l1,l2,…,ln的函数。由于f1和f2这两个优化目标相互之间矛盾性，因此建立如下所示的多目标优化模型：

根据机械手的运动学模型，雅可比矩阵中的连杆长度变量可以用d1、d2、d3、d4来表示，因此减少了优化变量，加快了优化计算速度。因此，最终的多目标优化设计模型为：

在拟人机械手的设计过程中，机械手的关节运动范围通常设置得比实际人体手臂关节的运动范围稍大。机械手各个关节的运动约束可以根据表1的数据确定。连杆长度参数的约束根据实际工作空间的需求而设置。拟人机械手的关节运动范围约束以及连杆长度参数的约束如表4所示。

表4 关节以及连杆长度的约束

3.2 多目标灰狼优化(MOGWO)算法

灰狼优化(GWO)算法是一种模拟灰狼种群的社会领导力和捕猎行为的群智能优化算法。为了对灰狼的社会等级进行数学建模，最优的解被认为是α狼，第二个和第三个次优解分别为β和δ狼。剩余的候选解为ω狼。在GWO中，优化过程受α、β和δ狼的指引，ω狼跟随这三者搜索最优解。

除了社会领导关系，为了模拟灰狼种群在捕猎过程中的包围行为，采用以下方程更新灰狼的位置：

D=|C·Xp(t)-X(t)|

(14)

X(t+1)=Xp(t)-A·D

(15)

式中，t表示当前迭代步；A和C为系数向量；Xp为猎物的位置向量；X表示灰狼的位置向量；·表示哈达玛乘积。

系数向量A和C计算如下：

A=2a·r1-a

(16)

C=2r2

(17)

式中，a的元素在迭代过程中从2线性减小到0；r1和r2为[0,1]之间的随机向量。

GWO算法利用模拟的社会领导关系和捕猎时对猎物的包围机制来寻找优化问题的最优解。该算法保存迄今为止获得的前3个最优解，其他个体根据这3组解更新自身的位置。在优化过程中每个个体根据以下公式来更新自身的位置搜索最优解的区域。

Dα=|C1·Xα-X|

(18)

Dβ=|C2·Xβ-X|

(19)

Dδ=|C3·Xδ-X|

(20)

X1=Xα-A1·Dα

(21)

X2=Xβ-A2·Dβ

(22)

X3=Xδ-A3·Dδ

(23)

(24)

为了将GWO算法扩展到多目标优化，在GWO算法基础上加入存档机制，将迄今为止搜索到的非支配帕累托最优解保存。同时引入领导选择策略从存档中选择α、β和δ解来领导灰狼个体的位置更新。

基于GWO扩展得到的MOGWO算法的主要步骤如下：

步骤1：初始化灰狼种群Xi(i=1,2,…,n)，初始化a、A、C；

步骤2：计算每个个体的目标函数值，找到非支配帕累托最优解并存档；

步骤3：在存档中选择Xα，Xβ，Xδ，t=1；

步骤4：当t小于最大迭代次数继续，否则转步骤9；

步骤5：根据式(18)～式(24)更新每个个体的位置，根据式(16)和式(17)更新a、A、C；

步骤6：计算每个个体的目标函数值，找到非支配帕累托最优解并更新存档；

步骤7：在存档中选择Xα，Xβ，Xδ；

步骤8：t=t+1，跳转到步骤4；

步骤9：算法终止，返回存档中的解。

MOGWO算法继承了GWO算法的特点，具有与GWO算法相似的收敛属性。两者的主要区别在于MOGWO算法围绕一组档案成员进行搜索，而GWO算法只保存迄今为止找到的前3个最优解。

3.3 优化模型求解

根据驱动和传动部分的性能参数，每个关节的刚度为Kq1=Kq2=6.5e5 N·m/rad，Kq3=Kq4=3.0e4 N·m/rad，Kq5=Kq6=5.8e3 N·m/rad，Kq7=3.0e3 N·m/rad。因此，拟人机械手的关节刚度矩阵(单位：N·m/rad)为：

Kq=diag(6.5e5 6.5e5 3.0e4 3.0e4 5.8e3 5.8e3 3.0e3)

根据MOGWO算法的搜索最优解的步骤，在MATLAB环境中对之前建立的多目标优化模型进行求解。其中，设置灰狼种群的大小为GreyWolves=100，MOGWO算法的最大迭代次数为MaxIt=500，存档大小为ArchiveSize=100。采用与多目标粒子群优化(MOPSO)算法类似的网格机制实现对Xα、Xβ、Xδ的选择以及当存档达到上限值时对存档进行删除、插入操作。因此，设置目标函数空间每一维度的网格数为nGrid=10，领导者选择压力参数和存档成员删除压力分别为beta=4，gamma=2。最终求解得到的非支配帕累托最优解如图4所示。

图4 多目标优化模型的非支配帕累托最优解

由图4所示的多目标优化求解结果可得，提升拟人机械手的可操作性指标与提高其端部刚度性能指标之间是相互矛盾的。追求单个性能的最优化会导致另一个性能的下降。因此，对拟人机械手的连杆长度的设计应该同时考虑这两个性能指标，根据实际的使用需求选择一个合理的解决方案。

为了研究拟人机械手的连杆长度参数对可操作性以及端部刚度的影响，分别选取f1和f2达到最大值所对应的非支配帕累托最优解，两个解之间的比较如表5所示。

表5 单独最优的非支配帕累托最优解比较

其中，*表示d4参数对可操作性以及端部刚度性能无影响，可在约束范围内根据需求选取。根据表5展示的结果可知，当单一的性能达到最优时，连杆长度参数分别接近约束的上、下边界，因此连杆长度的约束成为限制单一性能继续提升的主要因素。同时，根据表5所示的结果，f1相比于f2变化的幅度更大，说明连杆长度参数对可操作性能的影响大于对端部刚度性能的影响。

在获得d1、d2、d3、d4的最优解后，可根据d1、d2、d3、d4与l1、l2、l3、l4、l5、l6、l7之间的关系得到拟人机械手每个连杆的长度，实现拟人机械手的连杆长度设计，为后续的传动系统设计奠定基础。

4 结论

针对拟人机械手的连杆长度优化设计问题，基于螺旋理论建立了拟人机械手的运动学模型，并根据运动学模型得到相应的可操作性指标以及端部刚度性能指标。考虑到两个性能指标之间的矛盾性，建立了拟人机械手连杆长度参数的多目标优化模型。利用基于GWO算法扩展得到的MOGWO算法对多目标优化模型进行了求解。

求解结果显示，机械手的可操作性指标与端部刚度性能指标之间存在矛盾，单独提升一个性能会导致另一个性能下降。机械手的连杆长度参数的改变对可操作性指标的影响大于对端部刚度性能指标的影响。影响性能指标提升的主要因素为机械手连杆长度的约束。设计人员可以根据实际需求选择一组帕累托最优解作为机械手连杆长度参数的初步设计，将该优化算法应用于工业机器人三维数字化设计仿真平台上，可实现多种单组模型可重构优化(大于6种模型)。

由于只考虑了拟人机械手的连杆长度参数以及可操作性和端部刚度这两个性能指标，得到的优化设计结果无法体现出机械手的综合性能，因此，考虑更多性能指标以及包含更多结构设计参数的拟人机械手的优化设计值得进一步研究。