非对称结构索轮组位姿的精确求解方法
温新婕 吴晓光 樊俊宏 李越秀 虞丽芳
北京起重运输机械设计研究院有限公司 北京 100007
0 引言
高速大运量客运索道技术的发展对索道设计提出了更精确高效的要求。对于单线循环脱挂式索道、脉动索道以及单线固定索道等类型索道而言,索轮组是重要的线路设备。索道运行过程中索轮组位姿的确定是索道设计中关键一环。在不同线路不同的载荷工况下,线路上索轮组受力不同,钢丝绳的出入绳角度也不同,快速高效计算出不同绳折角情况下的各索轮位姿,可给索道的安全性和舒适性设计以及给其他相关设备如线路支架走台角度的设计提供依据。随着高速大运量客运索道线路动态特性研究的深入,建立线路设备等的理轮模型并进行动态仿真是今后索道系统研究的方向之一。
齐次变换方法是在多体系统研究中分析结构的常用方法。在工程机械领域也有广泛应用。文献[1]已经介绍了索道线路支撑结构,并以8轮组为例,基于齐次变换方法,推导了8轮组索轮轮心位姿坐标的解算方法,得出了位姿坐标的矩阵表达方式。但是通常索道轮组除了由对称结构轮组组成,如4,8,16轮组,还有许多非对称结构轮组,如6,10,12,14轮结构。对于对称结构轮组,其每对2轮组、4轮组、8轮组之间梁角度关系由于结构的对称性直接可得,从而可以直接用齐次变换求解。非对称轮组中结构的位姿由于索轮组和梁结构的非对称性,梁角度关系非直接可得,从而也不能直接用齐次变换方法求出轮组位姿,因而需要在分析结构关系的基础上,寻找求解方法。
1 非对称轮组结构
以6轮为例,轮组的结构如图1所示。6轮组索轮系统中,有3个2轮组,轮1、2铰接于轴3,轮4、5铰接于轴6,轮8、9铰接于轴10,轴3、6通过夹板连接,组成一组4轮组,该4轮组中心通过轴7铰接于索轮组大梁上,轴10另一端也铰接于索轮组大梁上,索轮组大梁通过可绕轴11转动,轴11通过固定支座固定在索道支架横担端部。本文中,两点间的距离表达为Li-j,i,j为点的标号。
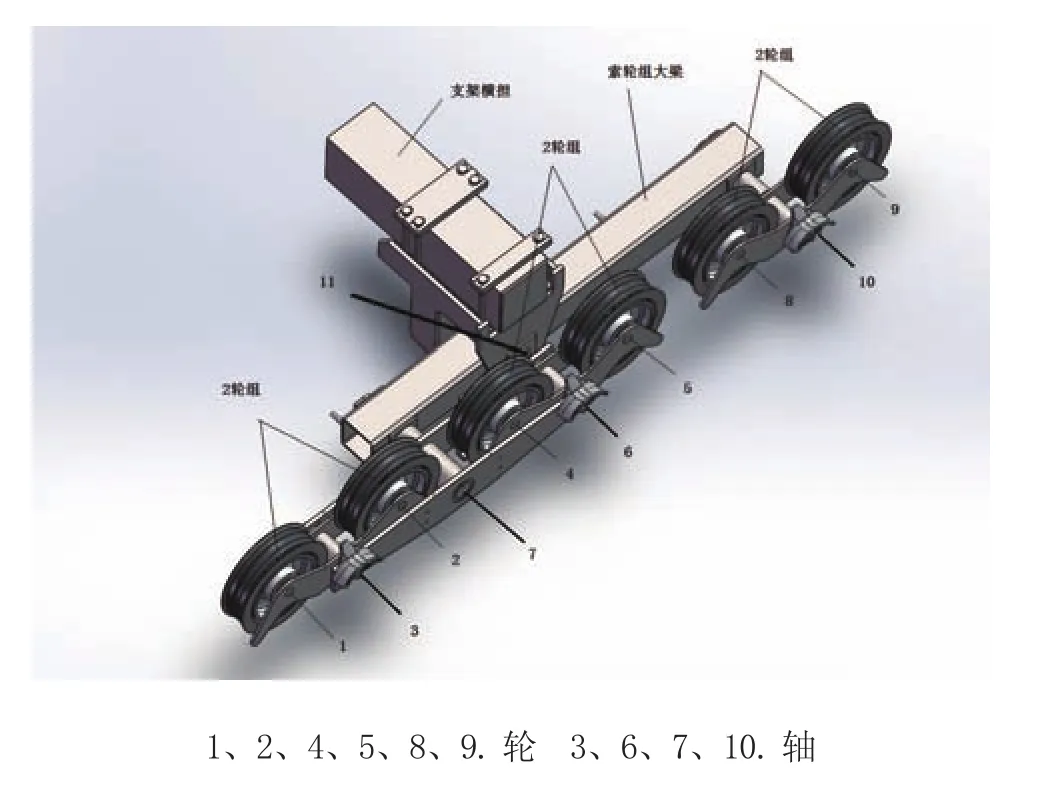
图1 6轮组结构图
根据结构布置可知

轮组设计时,6轮组结构和支座的铰接点11在L3距4轮组1/3处,即
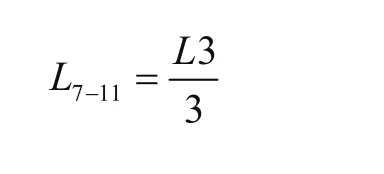
考虑折角关系的6轮组结构简图如图2所示。

图2 6轮组结构简图
索道支架上轮组的绳折角φ,每个轮上的绳折角为
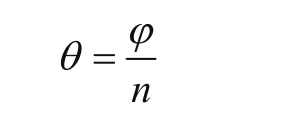
中间两轮组相对左侧两轮组转过2θ,最右侧两轮组相对左侧两轮组转过了4θ。
6轮组各轮的位姿问题即求解各轮心相对于铰轴11的位姿。
如图1,由于轮组结构的不对称性,对于已知每个轮上的绳折角,无法如对称结构轮组一样,直接由齐次变换得出梁L3的空间位置关系。
因每个轮上折角相等,且轮组为刚体假设。易知轮组4-5-6与轮组8-9-10在空间上对称,且L5-8与水平线的夹角为3θ。
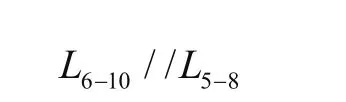
则在(X3,Y3)坐标系下点10坐标可求。
2 点10坐标求解
由参考文献[1]可知:4轮组1-7点在坐标系(X3,Y3)中坐标矩阵为

式中:Tn(i,j)为矩阵中第i行,j列对应的元素直线L6-10的方程为

整理上式并代入6点坐标值为
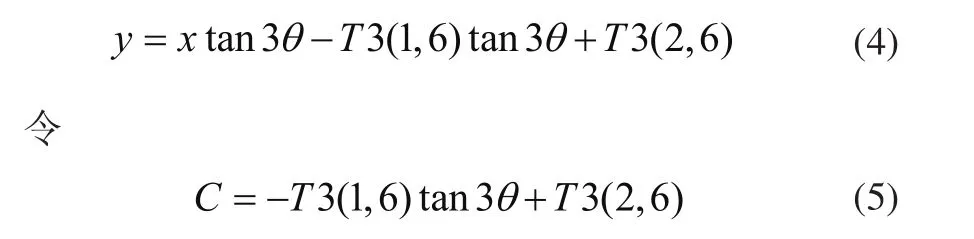

3 6轮组位姿齐次坐标求解
4轮组1-7点在坐标系(X3,Y3)中坐标矩阵已知,接下来需求解右侧两轮组中点8-9-10在坐标系(X4,Y4)中各点坐标。
3.1 右侧2轮组在坐标系(X4,Y4)中各点位姿
由文献[1]可知

4θ旋转转换矩阵为

T4即为所求。
3.2 组装6轮组(X5,Y5)坐标系中各点位姿
计算4轮组在(X5,Y5)坐标系中坐标T5A:即将4轮组平移矩阵为
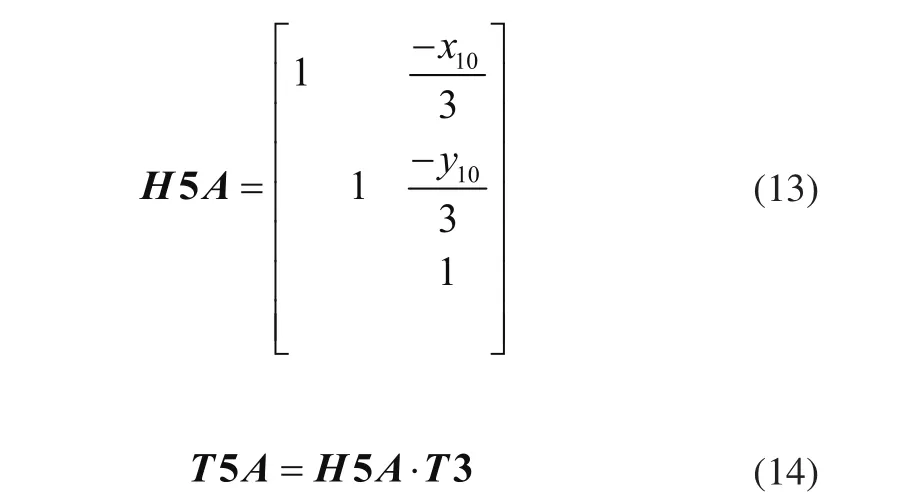
计算2轮组在(X5,Y5)坐标系中坐标T5B:即将2轮组平移矩阵为
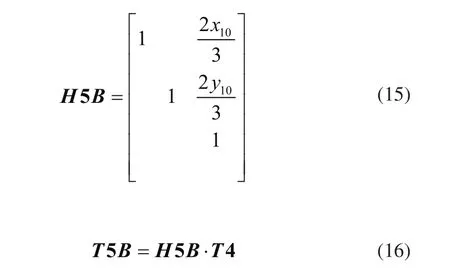
点11在坐标系(X5,Y5)中坐标为

组装1-11点在坐标系(X5,Y5)中坐标矩阵T5
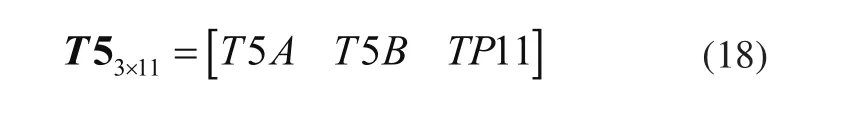
对应各列即为各点坐标。
参考参考文献[1]中同理可得入绳角φ1时水平坐标系(X,Y )坐标系中1-11点各轮心坐标矩阵为

式中:T6(i,1)为i点x坐标;T6(i,2)为i点y坐标。
4 结论
本文以6轮组为例给出了齐次坐标法求解非对称结构轮组位资中关键点的方程解法。并推导了计算公式,得出关键点的解析解。此方法可以类推到所有非对称结构轮组位姿分析。完善了等分折角条件下齐次坐标法求解对称和非对称索轮组结构的方法。在此基础上,可编写程序,提高索轮组位姿求解效率。进而索轮组与横担的相对位置关系,也可在用齐次坐标方法求解有倾角支架的横担位置之后计算得到,可用于更精确地确定线路支架的高度。在满足GB 12352—2018《客运架空索道安全规范》的前提下提高索道总体和部件设计的精度和效率。另外本文讨论的轮组位姿变化适用于吊具不经过索轮组时的情况。对于吊具经过索轮组时,索轮组的位姿变化及动力学特性,还需进一步研究。

