磁约束聚变堆托卡马克误差场研究进展综述

王辉辉

（中国科学院合肥物质科学研究院 等离子体物理研究所,安徽 合肥 230031）

0 引言

随着“双碳”需求的提出，能源结构调整也成为我国未来重要的发展方向。在众多能源中，具有清洁、安全、不受环境影响、取之不尽等优点的核聚变能是未来的理想能源。为了和平利用核聚变、获得稳定可控的核聚变能源，世界各国自20 世纪40 年代开始开展了大量的研究，陆续提出了磁约束、惯性约束等多种控制核聚变的方法。具有稳定输出特点的磁约束核聚变得到了广泛的研究。截至20 世纪90 年代，磁约束聚变托卡马克装置获得了能量增益因子Q（输出能量/输入能量）接近1 的参数区间，即托卡马克聚变装置中聚变反应的输出能量接近装置的输入能量，极大地鼓舞了核聚变研究人员，各种研究显示托卡马克是最接近未来聚变发电的可行方案。为此，国际上积极推动托卡马克形式的国际热核聚变反应堆（ITER）计划，希望验证托卡马克发电的科学可行性，开展聚变堆物理研究，找到未来聚变堆潜在运行模式并借此发现并解决各种工程技术问题。

托卡马克是由苏联库尔恰托夫研究所的阿齐莫维奇等人在20 世纪50 年代初发明[1-2]，它的原意由俄文的环形、真空室、磁、线圈四个词组成，主要原理是通过外部线圈产生的环向磁场将完全电离的放电气体（等离子体）约束在一个环形真空室中（见图1），再通过外部加热手段将这些等离子体加热到核聚变反应的条件。而如果要实现聚变发电，等离子体则需要达到自持燃烧的条件，即聚变反应自身产生的阿尔法粒子可以加热等离子体维持聚变反应持续下去，而不再需要外部加热手段。而在达到这个目标之前，还有许多物理问题需要一一解决[3-16]。

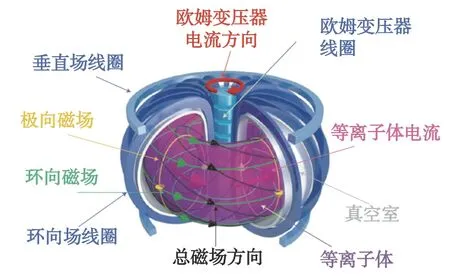
图1 现代托卡马克物理模型[17]Fig.1 Physical modeling of modern tokamaks[17]

误差场容易引起锁模是托卡马克物理专题中最重要的物理问题之一。国际上在20 世纪80 年代末在高参数等离子体中发现大量的锁模现象（旋转的等离子体突然停止转动，磁扰动信号突然增强，等离子体储能突然下降）[18-22]，可以直接引起等离子体破裂[20,22,23]，造成装置第一壁的损坏。即便不引起破裂，锁模也会导致等离子体储能下降20%～40%[18,21]。由于储能下降会造成芯部离子温度的大幅降低，因此会大大降低聚变堆核反应率，从而大大降低能量增益因子，导致聚变堆的经济性严重降低。为了避免锁模的发生，国际上自20 世纪90 年代初以来，科研人员在国际各大主流装置上通过外加误差场（共振磁扰动，RMP）开展了大量的误差场锁模研究[5,11,24-59]。与此同时，开展了大量的理论解析与数值模拟研究，尝试阐明锁模基本物理过程及误差场与各类参数之间的规律[24,37,60-81]。同时，国际上各大装置在进行物理设计时，都将误差场问题摆到重要的位置。在物理设计阶段研究误差场问题的步骤如下：（1）基于以往的实验或理论结果，外推评估装置在主要运行参数区间所能承受的不至于引起锁模的误差场幅值大小；（2）通过工程分析，判断该误差场幅值需要的工程精度的范围；（3）以现有工程精度，判断装置的误差场是否需要校正；（4）物理设计校正场线圈及配套电源所需能力。例如，目前ITER 装置在经过十多年众多的实验评估和理论评估基础上，设计了结构复杂的超导校正场线圈系统，见图2。该系统有18 组线圈，与ITER 的纵场线圈数量相同，并且配套的电源系统数量也与纵场线圈数量相同，由此可见误差场在托卡马克中的重要性。此外，目前国际上较大的托卡马克装置如JT-60SA[82]，JET[29]以及未来的紧凑型聚变装置SPARC[83]都设计了校正场线圈来降低装置自身误差场避免锁模的发生。由于误差场的重要性及快速进展，国际托卡马克物理活动（ITPA）于2021 年将磁流体专题中的高优先度问题全部列为误差场研究。

图2 ITER 18 个校正场线圈与中心螺线管及6 个极向场线圈的全景图[84]Fig.2 Overrall view of the 18 ITER error field correction coils with the central solenoid and the 6 poloidal field coils[84]

误差场研究尽管开展了四十多年，但是迄今没有比较完整的综述文章。为了让读者对托卡马克误差场锁模物理研究有较为清晰系统的认识，本文在笔者博士论文绪论基础上[85]，结合误差场近年研究，基于历史发展脉络，梳理给出各个发展阶段的重点研究内容及主要关注点，将实验、理论和模拟融入历史发展过程，而不再将实验、理论、模拟单独作为章节分别介绍。本文分为以下五个部分：第一部分为早期历史，介绍误差场锁模早期理论准备及初步实验；第二部分为理论形成阶段，该阶段主要侧重于理论发展对实验现象的定性分析；第三部分为理论与实验结合阶段，该阶段主要关注点是理论与实验的自洽性验证、对未来聚变堆外推以及新现象的发现与解释方面；第四部分为其他方面应用介绍，该部分主要介绍误差场相关理论的应用拓展及校正场/共振磁扰动线圈的其他应用；最后一部分为结论与展望，本部分将指出目前误差场锁模研究尚未解决的物理问题以及未来的发展方向。

1 早期历史

在该阶段追溯了误差场早期实验和理论的前期准备（见图3），在该阶段的后期，国际上几个大装置，如JET[18,21,22]，DIII[86]，TFTR[87]和JT-60[19]，在迄今托卡马克最高参数条件下均观察到了锁模及撕裂模现象，这些都伴随着储能的大幅下降甚至等离子体破裂，因此，国际上对撕裂模，尤其对锁模越来越重视并开展广泛的研究。

图3 误差场研究早期历史发展Fig.3 Early history of error field research

误差场在托卡马克中的实验研究可以追溯到1974 年日本的JFT-2 托卡马克上，作者通过外加共振磁扰动线圈研究了磁岛宽度与误差场幅度、磁剪切之间的定标关系[88]。需要指出的是，当时的研究还没有涉及到误差场慢化等离子体转动进而锁模的物理内容。1979 年，Waddell 等人通过将原先的柱形程序改成包含不同模式耦合项的三维柱形程序，详细研究了2/1 (m/n)模与3/2 模耦合与非耦合下的演化情况[89]。作者在文中也用理论简要地进行了讨论。可以看出2/1 模充当了3/2 模误差场的角色，而3/2 模在演化后期通过与2/1 模的耦合自发调整到一个合适的大小，最后诱发了等离子体的破裂。三维环形耦合的研究使人们认识到不同撕裂模的相互耦合是诱发破裂的重要原因。也就是说，不同撕裂模的相互耦合可以看做其中一个撕裂模为另一个撕裂模的误差场源，两者耦合则互为误差场源。

1980 年，董家齐和石小麟等人已经关注到托卡马克中(导体壳切口引起的)误差场会在共振面产生磁岛，对其进行了数值研究并对外加扰动场抵消误差场进行了细致的探讨[90]。从这里可以看出国内误差场的研究也起步得比较早并且研究得比较充分(包括柱形和环形情况的分析)。他们接下来还研究了误差场对等离子体平衡的影响效果[91]。

1980 年，Jensen 和华裔学者朱明盛将低频转动误差场引入到撕裂模上并进行了线性分析[92]。该文章注意到了边界磁扰动在有理面上的磁通跳跃(∆′)是复数，不过只做了本正值分析，分析了可能涉及增长率等，当时还没有将这个复数的磁通跳跃与误差场锁模联系到一起。1981 年，Boozer 通过理论分析仔细研究了转动外扭曲模在电阻壁作用下，初始转动受到阻尼的情况(即转动下的电阻壁模)[93]。文章篇幅虽不足两页，但是文中理论分析对后来误差场锁模及电阻壁模的理论发展却发挥了至关重要的作用。1983 年，Jensen 和朱明盛在Boozer 文章的基础上将1980 年的工作加上一个等离子体流(本质上相当于1980 年工作的重新解读)进行了分析，文中详细分析了磁通跳跃实部与虚部的原因，指出实部表示能量在奇异层被吸收，而虚部表示动量在奇异层的转移[94]。这篇文章就误差场阻尼等离子体流速给出了清晰的物理图像，可以算作误差场锁模最关键的原始文献。

1983 年，Hu 通过线性理论分析了受迫重联的物理模型，对不同时间尺度下内区外区进行了详细的分析，并且考虑了等离子体静止、外加转动误差场的情况[95]。分析得出等离子体静止情况下，外加转动误差场通过j×B的电磁力将内区等离子体加速，这是首次提出电磁力概念的文章(Jensen 和朱明盛1983年文章中侧重于说明阿尔芬波与奇异层之间的动量转移，没有从宏观的角度说明)。然而由于文章重点不突出，因此没有引起太多关注。1985 年，Hahm 和Kulsrud 用与Hu 类似的模型重新研究了受迫重联，研究重点在固定边界扰动(相当于固定误差场)重联率随时间的演化情况，将线性演化分为四个时间段，进行了分别讨论，并在后面通过拉普拉斯变换将线性理论很好地展现出来[96]。在文章的后面，作者也将边界扰动的情况应用到非线性的Rutherford 撕裂模上，此外作者还就边界扰动幅度随时间变化的情况进行了分析。这篇文章对于后面误差场锁模理论的建立也有着比较重要的作用。

1988 年，Lazzaro 和Nave 从实验研究的角度对前面在JET 上开展的等离子体转动条件下共振磁扰动(RMP)主动控制磁岛的研究进行了分析[97]。他们在文中进行了详细的理论分析并给出了对应的实验结果，这些实验结果在定性上都比较符合所得的理论。1989 年，Berge 等人将理想磁流体方程线性化后，通过扰动磁通函数(ψ)来表示电磁力，里面的很多细节都表述得很清楚[98]。然而没有指出可以将误差场作为边界条件。文中的附录部分考虑了电阻壁的边界，不过没有给出一个可供实际应用的结论，所以该文章所受关注也不太多。同样在1989 年，Hender等人也研究了电阻壁对撕裂模的作用，发现电阻壁中的非线性涡状电流可以慢化等离子体转动，且在等离子体转速足够快时可以稳定驱动引起的撕裂模[99]。

以上都可以算作误差场锁模的早期历史，可以看出误差场锁模早期发展主要集中在理论的构建上。

2 理论形成阶段

该阶段主要侧重于锁模实验现象的物理理解上，此阶段众多理论学家从不同角度发展了磁流体下的误差场锁模理论，到1998 年磁流体下的误差场锁模理论发展成熟（发展简图见图4）。同时，基于理论分析和实验结果，研究人员也针对ITER 欧姆低密度放电对锁模所需的误差场阈值进行了外推判断。

图4 误差场研究理论形成期发展简图，磁约束聚变理论界多个知名学者对理论发展做出了贡献Fig.4 The sketch of forming period of error field theory，many recognized theoretical physicists in magnetically confined fusion field promoting the theoretical development of error field locked modes

1990 年，Nave 和Wesson 详细分析了包含电阻壁的非线性锁模理论，里面给出的电磁力表达式就是后来完整理论的原型，文中专门就电磁力的细节进行了讨论[60]。作者还通过JET 实验数据进行模拟，得出的结论定性地解释了实验，这也是误差场理论与实验结合的典范文章(当然其中有些东西还没有仔细分析，例如非线性锁模需要满足什么条件？)。此外，作者在文章的讨论部分也在动量方程中加入了粘滞项，这也为后面理论发展提供了方向。因此，这篇文章应该算作理论形成期的第一篇文章。

1991 年误差场锁模研究取得了多方面的进展。Fitzpatrick 和Hender 对Hahm 和Kulsrud 的受迫重联模型进行了扩展，让边界扰动随时间周期性变化，这样构建了误差场锁模模型，这个模型的建立让我们可以较方便进行锁模相关研究[61]。文中大致探讨了线性与非线性的情况，当然还没有对粘滞力与电磁力进行讨论。Jensen 等人就转动对误差场的影响进行了研究，其研究中最有用的信息是指出粘滞力对等离子体拖拽的重要作用，这向锁模平衡理论的建立又迈进了一步[63]。Reiman 和Monticello 在自生磁岛和误差场诱发磁岛两种情况分别对磁通跳跃展开了讨论，这也为误差场渗透理论的建立提供了一个参考[100]。Scoville 等人在DIII-D 装置上开展了锁模研究，研究了n=1 的撕裂模锁模情况，并对临界岛宽进行了理论分析[25]。

1992 年，Hender 等人在COMPASS-C 装置上对外加静止共振磁扰动线圈下的一系列放电现象进行了研究[24]。文中进行了锁模研究，对锁模与非锁定进行了一系列观测并对锁模情况下的电子密度与外加共振磁扰动线圈中电流强度（正比于误差场幅度）进行了拟合。其中还仔细分析了软X 射线及真空紫外线光谱情况下的速度，并对边界粒子约束与再循环进行了分析。此外文中在附录部分还就粘滞力进行了讨论，并写出了电磁力与粘滞力的力平衡方程。La Haye 等人通过对DIII-D 和COMPASS-C 两个装置上误差场幅值与电子密度、托卡马克大半径及环向磁场的定标，外推出ITER 上欧姆放电情形下误差场锁模幅值与环向磁场之比Br21/BT≈2×10−5[27]。这样一来，我们便可得出ITER 若消除锁模需要足够的工程精度或者我们可以通过中性束注入的方法提高等离子体转速也可有效避免锁模，这说明误差场对ITER 的影响之大。

1993 年，这一年误差场锁模理论初步建立起来。Fitzpatrick 在柱形几何位形下撕裂模与外部结构相互作用的文章中对误差场锁模理论进行了详细的分析与讨论。将锁模过程分成五种类型，其中模式渗透这种类型对以后误差场锁模理论的发展起到了非常重要的作用[65]。此外文中还对电阻壁下转动磁岛的慢化进行了详细的分析，这些也是对以往相关模型的深化。当然文中的观点基本都是在有理面为常磁通假设基础上得来的，而实际上非常磁通情况也具有重要的地位，它将是后面发展的重要方向。同年，Fitzpatrick 等人还分析了线性和非线性情况下差动转动下的耦合撕裂模，并用T7 code 进行了模拟[66]。Jensen 等人也注意到了粘滞力的作用，将粘滞力与电磁力作为同等重要的因素考虑了进来[101]。

1994 年，Fitzpatrick 研究了撕裂模与扭曲模耦合下的稳定性，文中对单个有理面、两个有理面及多个有理面上两种模进行了广泛的研究，但是文中最有价值的研究为附录B[102]。附录B 对不可压缩下内区磁流体方程下欧姆定律和涡方程进行了详细的讨论，将线性层机制分为四种机制，这在以后误差场锁模理论的统一及后面多元化发展时期均起到了至关重要的作用。

1995 年，Hurricane 等人通过数值模拟讨论了边界有误差场情况下平衡时，有磁岛与无磁岛两种情况下的转动等离子体得出：无磁岛时，边界通过阿尔芬共振与等离子体交换动量；有磁岛时，边界通过电磁力与粘性力交换动量，这在后面的统一理论中也起到了一定的作用[103]。1995 年，Fitzpatrick 在威斯康星大学暑期学校的讲义中也对误差场进行了归纳和总结[104]。

1996 年，Boozer 在1995 年Hurricane 等人数值模拟基础上从理论上对等离子体转动对共振磁扰动的屏蔽进行了分析[105]。文章中最有价值的当属探讨了扰动磁通函数在等离子体中的位移，这个量在外区和内区中的区别及内区中的奇异性在误差场统一理论中也得到了探讨。最近的研究中显示等离子体位移等因为没有充分理解而再次得到探讨[106]。

这里将在统一理论中起到重要作用的王晓钢及合作者的文章单列出来。1992 年，王晓钢等人就注意到驱动重联Taylor 模型下的理论分析中奇异层会出现电流片，并用Sweet-Parker 模型进行了简要讨论[107]。1996 年，马志为与王晓钢等人通过理论分析和数值模拟研究了等离子体在非转动和转动两种情况下由误差场产生的电流片[108]。1997 年，王晓钢与Bhattacharjee又进一步对转动等离子体中误差场锁模进行了理论分析，强调了Sweet-Parker 模型的重要性[64]。

1997 年，La Haye 提交了ITER 锁模物理的报告，基于已经发展的理论和已有的COMPASS-C、DIIID 和JET 上误差场锁模实验结果，基于Neo-Alcator能量约束时间及电子逆磁漂移频率与大半径的假设，换算成托卡马克大半径，对ITER 低密度欧姆下的误差场进行了外推评估，评估得出ITER 误差场诱发锁模的阈值非常低，约Br21/BT≈2×10−5。而消除锁模的方法是通过反向中性束注入的方式，或者在保证纵场及极向场线圈安装精度在万分之一以内情况下，通过校正场线圈进行校正[53]。需要指出的是，当时ITER 的大半径是8.1 m。

截至1997 年，误差场锁模理论影响比较大的一共有三支研究小组：主要通过常磁通假设进行研究的Fitzpatrick 及合作者；探讨阿尔芬共振的Jensen及合作者；侧重于Sweet-Parker 理论研究的王晓钢及合作者。

1998 年，Fitzpatrick 结合以前自己与合作者的研究及王晓钢等人、Jensen 等人的研究，对误差场锁模理论进行了分析与整合，最后给出了磁流体下误差场渗透的完整理论，理论包含了线性部分和非线性部分，并在文章后面给出了统一理论及相关实验应用[67]。至此磁流体框架下的误差场锁模理论完全建立起来。

3 理论与实验结合阶段

自1998 年以后至2021 年的20 多年时间内，一系列实验装置进行了误差场锁模的研究。例如TEXTU[109]、DIII-D[28,30,32,33,35,38,39,45,78,110-118]、COMPASS-D[28]、JET[28-30]、ALCATOR C-MOD[51]、TEXTOR[40,119]、MAST[50]、NSTX[37,49,52,120]、J-TEXT[41,55,79,121]、EAST[42-47,118,122,123]、KSTAR[58,59,124]等。这些装置实验主要目的是通过这些装置的参数定标来找到不依赖装置、统一的物理规律以便外推到未来聚变堆，如ITER 等锁模时误差场的阈值（影响误差场锁模阈值的相关参数定标）以及判定引起锁模的误差场模式（涉及到误差场度量标准）。为了解释实验，误差场锁模理论也从磁流体理论向双流体理论和动理学理论方面拓展。同时，理论也从误差场的共振分量向非共振分量进行了拓展[125]，并成为动量输运研究的重要课题。2012 年，Fitzpatrick 将Cole 和Fitzpatrick在2006 年研究的线性漂移流体误差场渗透理论扩展到了非线性部分，并针对目前很多托卡马克误差场幅度与电子密度的线性定标展开了讨论[73]。这些研究有效推动了误差场锁模理论的完善。此外，在误差场数值模拟方面，虞清泉及合作者[75,126-128]、刘钺强及合作者[80,129,130]近年来也开展了许多有意义的研究工作。此外，笔者发现磁流体框架下的误差场锁模经典理论[67]存在的错误，重新给出了正确的非线性过渡机制理论并通过数值模拟证实了笔者的发现[79]。在开展实验和理论、模拟研究的同时，各大装置也据此深入开展了误差场容忍度的评估[37,42,58,59,110,117,131-134]，希望通过外推给出现有装置误差场水平、可承受的误差场最大幅值、未来聚变堆，如ITER 等装置的误差场容忍度，并在工程极限范围内开展校正场的物理及工程设计。本部分将根据误差场研究关注的问题展开讨论，分别介绍误差场锁模参数定标进展、误差场校正度量标准进展以及高参数下误差场锁模进展。

3.1 误差场锁模参数定标进展

等离子体发生锁模时的误差场阈值与各种参数之间的依赖关系是决定准确外推到未来聚变堆装置的关键问题，该问题也是误差场研究的核心问题。如果理论跟实验结果相差巨大却无法解释其中的原因，那么理论外推评估未来聚变堆的误差场容忍度就会给出错误的结论。而影响锁模的误差场阈值的相关参数超过七个，从实验的角度也无法从七个维度上展开海量的数据扫描（实验无法横跨七个以上维度的巨大参数范围），因此基于实验验证后的理论才是外推评估聚变堆误差场容忍度的理想选择。因此，一直以来，无论理论学家还是实验物理学家都试图给出统一的结论，然而该问题二十多年一直没有得到解决[43]。

其中最主要的关注点在于理论上密度定标与实验上密度定标的巨大差异。Fitzpatrick 发现其之前在众多知名理论学家基础上发展起来给出的磁流体下误差场锁模统一理论[67]，得出的误差场锁模阈值与密度无关，为此否定了自己的理论[73]，尝试发展新理论，将理论从磁流体发展到双流体线性理论[70]、双流体非线性理论[73]，尽管如此，都难以自洽解释实验中观测到的误差场与密度的强依赖关系[24,28-30,37,40,50,51,119,120,135]。需要指出的是，这些实验大多都是实验统计结果，很少给出详细的理论分析。另一方面，从1992 年的COMPASS-C[24]、2002 年的DIII-D[30]、2014 年的JTEXT[41,79]的实验解释上，可以看出通过假定理论中的动量约束时间与密度无关[24,30,79]，或者在模拟中预设动量约束时间不变[41]，均自洽解释了实验结果。而Fitzpatrick 之前基于无法解释实验中的密度定标而否定自己发展统一的误差场锁模经典理论所使用的理论分析有个前提假设：动量约束时间假定遵循托卡马克中低密度下能量约束时间满足的Neo-Alcator 定标（线性欧姆约束定标），即假定动量约束时间与密度呈线性关系。使用该假设后，经典理论得出误差场阈值与密度无关的关系[84]。由此可见，从实验上判定该假设是检验理论能否解释实验的关键。

基于这个思路，笔者等在EAST 托卡马克装置设计了多组欧姆加热下误差场锁模的密度定标实验[43]。通过实验发现EAST 上这些欧姆加热下的误差场锁模密度定标实验的能量约束时间基本与密度无关，相当于处于饱和欧姆约束区间，不处于Fitzpatrick 基于实验常识假定的线性欧姆约束区间。笔者还通过对这些实验参数进行详细的物理区间分析，指出这些实验所对应的物理机制。如果物理机制中的其他量都与密度无关，那么可以直接依据理论给出对应物理区间的定标结果。可以得出该物理区间下误差场与密度定标与实验结果大致相当。而实际上单独的密度扫描也会带来如电子温度等相关物理量的变化，笔者将经典理论转化到可以用于实验分析的公式，对实验中各个相关的参量都从实验上给出定标，给出的基于实验判定的理论定标与实验直接观测到的密度定标一致，自洽解释了欧姆加热下密度定标的实验结果（见图5）[43]。该结果最早在2016 年以笔者邀请报告的形式在美国磁流体稳定性控制研讨会上公开报道[136]。报道后，韩国KSTAR 于2018 年和2019 年，美国DIII-D 于2019年和2020 年在ITPA MDC-19 的误差场专题报告中进一步验证了EAST 上的结果。这些进展表明经典理论可以自洽解释实验结果，基本证实了理论外推评估聚变堆装置误差场容忍度的可行性。在取得这个突破后，随后，笔者等基于EAST 进一步开展并自洽解释了误差场锁模下的纵场定标（包括欧姆加热和射频波加热）以及边界安全因子定标的实验结果[44]。为了进一步验证经典理论的适用范围，笔者等进一步开展并自洽解释了射频波加热下误差场锁模的密度定标[46]。

图5 理论自洽解释EAST 上欧姆加热下误差场锁模密度定标（更新版）[43]Fig.5 Theoretical analysis is consistent with experimental observation of error field locked mode density scaling in ohmically heated discharges in EAST[43]

3.2 误差场校正度量标准进展

度量标准的确立是误差场研究的另一个重要问题。误差场引起锁模首先需要判断究竟是哪一个或哪一些误差场分量在什么位置起到关键作用。之前在各大装置上观测到的自然锁模或者通过外加共振磁扰动激发的锁模影响约束比较大的一般都是m/n=2/1 撕裂模，因此选定无等离子体下2/1 面对应位置处的共振分量作为误差场校正对象。通过初步理论分析，得出相邻有理面上的对应共振分量也会通过粘滞和环向耦合效应对锁模阈值有所贡献[5,132]，经过DIII-D 上误差场校正补偿实验，初步验证了模式耦合效应[132]，由此三模耦合校正判据成为各大装置及ITER 正式校正标准[11]。

三模耦合判据作为误差场校正标准还没有广泛应用便被发现难以解释一些装置的误差场校正实验，继而被新的重叠场校正标准所取代[137]。NSTX 和DIII-D 装置在优化校正场线圈谱形降低校正场的实验中发现总的共振场实际上是增加而非减小。为了解释这个现象，Park 等人通过扰动平衡考虑了屏蔽电流的响应对外加扰动磁场的贡献，该研究中包含了非圆截面中极向模数的耦合效应（见图6）[49]。该研究发现非共振分量在总的共振场中的贡献远远大于共振场的贡献，发现三模耦合校正判据不能解释共振磁扰动谱形变化下的实验结果[49]。此后，关于不同谱形下的误差场锁模研究陆续在各大装置上开展并证实误差场锁模中谱形的相关性[38,39,42,47,48,59,110]。既然非共振分量起作用，那么不同磁扰动谱形下固有误差场幅值及方向如果不同将直接影响到后续的校正方案。如果差距较大，这意味着还需要重新给出校正标准，对误差场的非共振分量一并校正。尽管目前多个装置，如NSTX[138]，MAST[50,139]，DIII-D[35,110,112]，J-TEXT[56]，ASDEX-U[140]，KSTAR[58,59]等开展了固有误差场评估（其中DIII-D 上开展了多次误差场校正实验[38,48,114,117]），但是一直没有这方面的实验证据。而该模型能否消除不同谱形下固有误差场幅值及方向上的可能差异，也迫切需要在实验的基础上开展进一步模拟分析进行判断。基于此，笔者与合作者在EAST 上开展了不同谱形下固有误差场评估的一系列实验，发现共振与非共振两种磁扰动谱形下，固有误差场幅值高达七倍的差距，进一步通过MARSF 模拟等离子体响应指出目前的重叠场模型还不足以解释该差异，还需要进一步发展[42]。此外，KSTAR[58,59]和EAST[42,47]两个装置与ITER 同样都是全超导托卡马克，两个装置实验发现固有误差场都比较小，这对ITER 来说是比较好的消息。尽管如此，由误差场经验定标外推到ITER，现有的工程精度也同样得出ITER 需要校正。

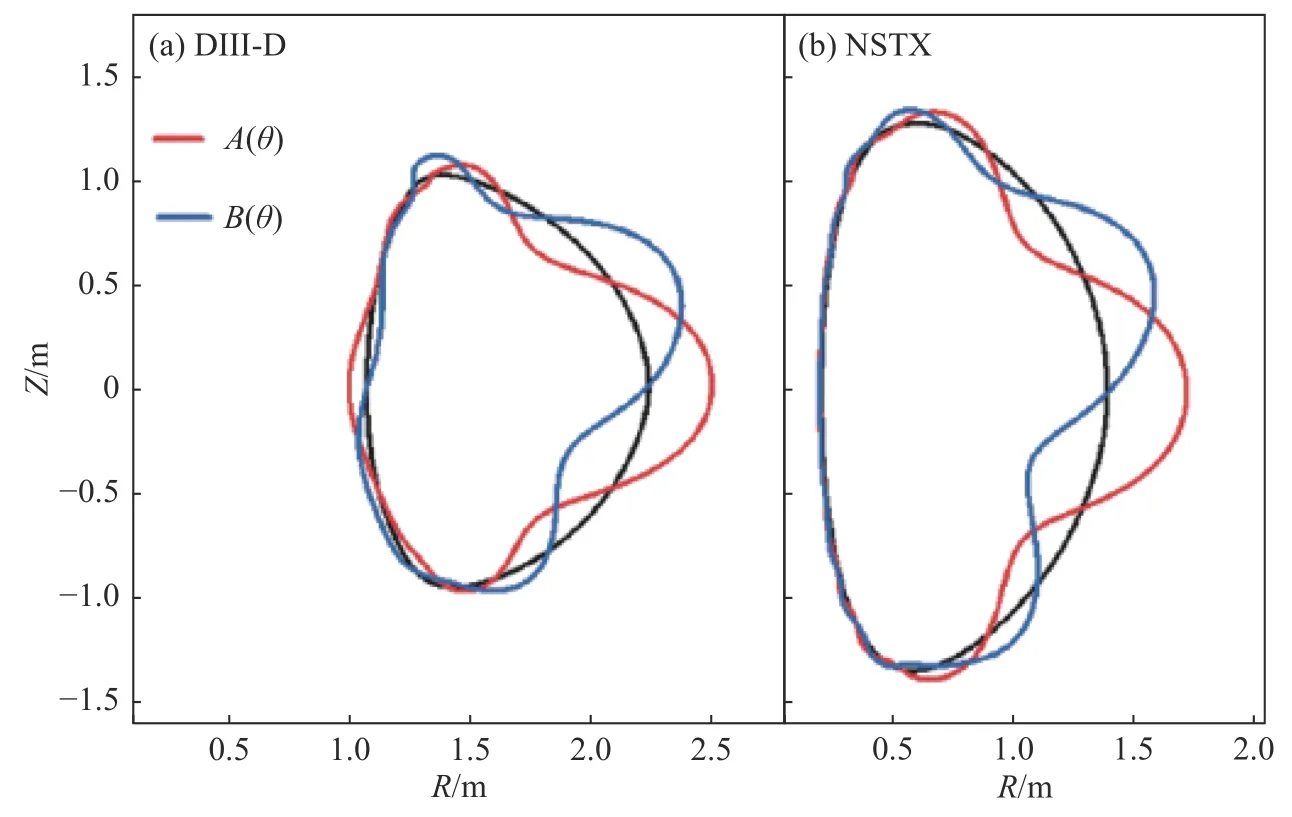
图6 等离子体边界处的磁扰动分布使有理面上总的共振场最大化[49]Fig.6 The distributions of the external field on the plasma boundary maximizing the total resonant fields on rational surfaces,for (a) DIII-D and (b) NSTX[49]

在非共振物理中，理论上也有新的模型被提出。2007 年Cole 等人将向克强等人的非共振磁扰动引起环向粘性的结果应用到欧姆加热下的误差场渗透理论中，研究表明非共振磁扰动引起的新经典环向粘滞(NTV)可以减小误差场锁模的发生，这是误差场渗透理论的又一拓展[125]。随后，Cole 等人又给出了详细的讨论[141]。2010 年NSTX 上基于NTV 模型的计算成功校正了非共振误差场[142]。同年，孙有文等人在JET 托卡马克中研究中新经典环向粘性对等离子体环向转动的制动效应[143]，并将2007 年Cole等人的理论推广到无碰撞的情况[144]。2011 年Callen从理论角度对三维磁扰动理论及相关实验研究进行了综述，重点介绍了NTV 方面的一些进展[145]。这些研究使误差场校正逐步走向详细的定量分析阶段。尽管如此，现有基于等离子体响应的校正标准还需要进一步确定。

3.3 高参数下误差场锁模进展

从逻辑上来说，本节属于3.1 的内容，但是由于三个原因使得有必要将高参数下误差场锁模研究单列出来：（1）误差场锁模经典理论仅仅关注欧姆加热等较低参数下的实验结果，没有考虑到等离子体比压效应也会对误差场有放大效应[67]；（2）不同比压下对应不同运行模式和理论极限，这也意味着误差场锁模理论将采取不同的理论模型；（3）未来聚变堆运行在高参数区间，对该区间的误差场容忍度，即锁模的误差场阈值评估至关重要。误差场锁模的比压效应最早于1992 年在DIII-D 上被发现[26]，但是没有引起理论学家的重视[5,29]。直到2001 年，Boozer 发 展理论解释实验上观测到的电阻壁模（RWM）在临近比压极限时的共振场放大（RFA）效应现象后[146]，误差场锁模阈值的比压效应才慢慢得到关注和研究[33,37,44,46,120]，图7 为DIII-D 上观测到的误差场锁模阈值随等离子体比压增大而减小的现象[33]。从上面可以看出，低参数下的误差场锁模研究无论实验还是理论都有了比较多的研究，并基本得到了自洽验证，而高参数/不同比压下的误差场锁模研究，无论从理论还是实验角度，都还处于起步阶段。由于聚变堆如ITER 等主要运行在低旋转区间，而目前像DIII-D、NSTX 和KSTAR 等研究误差场锁模的主流装置主要通过中性束注入加热，在更高参数下将会远离如ITER 等装置的低旋转区间，而目前像EAST托卡马克以射频波加热为主，更加有利于运行在低动量注入的高参数区间，因此，在EAST 装置上开展误差场锁模对于低旋转下误差场锁模物理将有更重要的价值。笔者及合作者基于EAST 开展并通过理论自洽解释了射频波加热下的纵场定标研究及密度定标研究[44,46]。在EAST 上针对不同比压下的物理研究中也发现了等离子体比压对误差场的放大效应，相关文章正在整理中。

图7 DIII-D 上外加场诱发2/1 模与等离子体比压关系[33]Fig.7 Applied field required to induce 2/1 mode versus plasma normalized β in DIII-D[33]

4 其他方面应用介绍

本部分介绍误差场相关理论的应用拓展及之前用于误差场研究的共振磁扰动线圈及校正场线圈的其他方面应用。这三种应用分别为：（1）边界局域模（ELM）的控制；（2）电阻壁模（RWM）的动态控制；（3）激发新经典撕裂模（NTM）的种子磁岛的产生。其中共振磁扰动控制边界局域模的理论与误差场锁模的理论有较为密切的联系，电阻壁模与误差场的放大效应有关，新经典撕裂模是锁模产生撕裂模之后重要的阶段，因此，这三种应用也可以看作误差场锁模研究的深化及细化。

4.1 边界局域模的控制

2004 年，Evans 等人在DIII-D 上通过共振磁扰动线圈成功抑制了边界局域模(ELM)，这次实验引起了极大的关注，至此共振磁扰动(RMP)线圈已经不仅仅属于误差场锁模研究所专有[147]。后面的发展让我们意识到RMP 几乎是连接ELM 的代名词。实验抑制结果见图8。2005、2006 年，Evans 等又针对ELM 作了一系列研究对其物理机制进行了一些探讨[148-150]，然而至今仍然没有很好的理论可以很好地解释这一实验结果[151]。因此，共振磁扰动抑制边界局域模的相关物理也是目前国际上的前沿课题。自此之后，JET[152,153]、MAST[153-156]、ASDEX-U[153,157,158]、KSTAR[153,159-161]、EAST[162-165]等装置陆续开展了共振磁扰动控制边界局域模的研究，其中EAST 装置甚至在高环向模式（n=4）下成功实现了ELM 的抑制[164]。在边界局域模的理论解释上，最近有一系列理论模型被提出[151,153,156,166-169]。目前比较认同的RMP 对ELM 的缓解物理机制是RMP 通过非线性耦合将高n气球模不稳定的ELM 弛豫到更小的环向模数[168]。此外，Diamond 与Loconte 通过Hasagawa-Wakatani方程建立了共振磁扰动与漂移波湍流-带状流之间的相互耦合机制[170,171]。而现有的理论还不足以完全解释随机磁扰动对边界局域模的抑制，因此相关的物理机制还需要不断地完善。

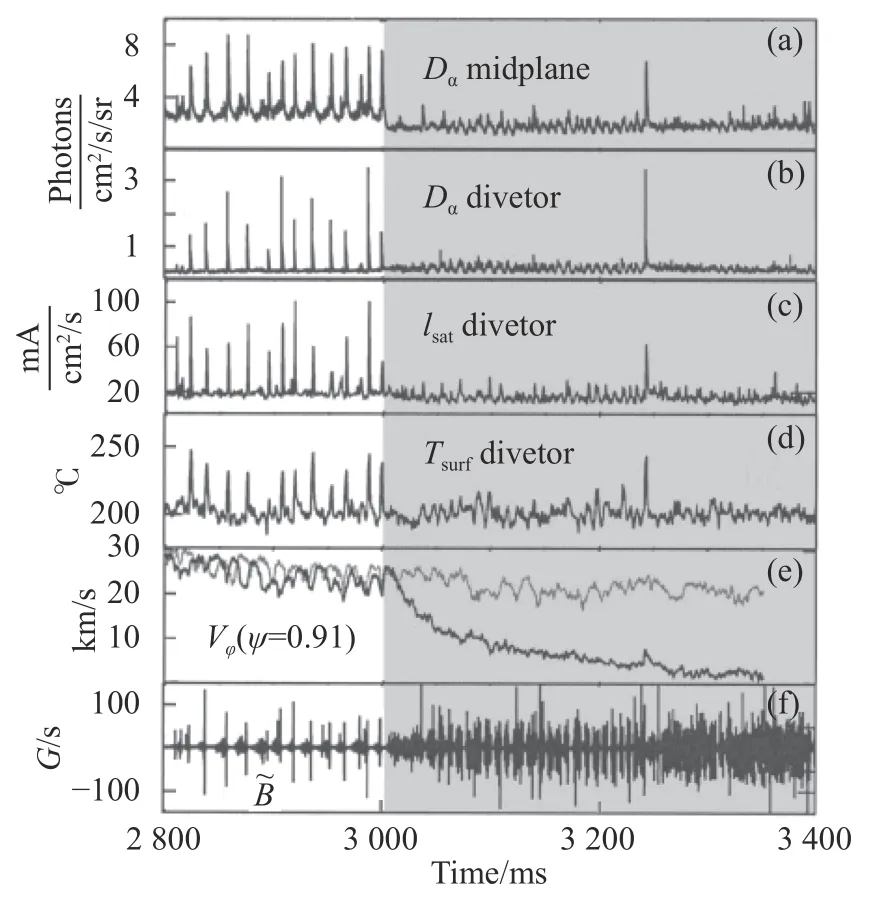
图8 DIII-D 托卡马克上共振磁扰动抑制边界局域模，阴影部分为共振磁扰动线圈通上电流4.4 kA 时间段[147]Fig.8 Resonant magnetic perturbations (RMP) suppress edge localized modes (ELM) in DIII-D tokamak,the dashed region indicates the time when the I coil is pulsed on with a current of 4.4 kA[147]

4.2 电阻壁模的动态控制

电阻壁模是未来聚变堆运行超过理想比压极限后遇到的重要的宏观不稳定性[172-175]。其物理图像是将等离子体看作刚性流体，流体在整体扭曲变形（外扭曲模）后，在理想真空室金属壁（无电阻）产生的涡流的反作用力下，扭曲变形被抑制，但是由于真空室金属壁不是理想导体而有一定的电阻，因此整体扭曲并不能被完全抑制，因此外扭曲模会在真空室金属壁电阻下缓慢增长。控制电阻壁模有两种方式：（1）增加等离子体整体旋转，使旋转克服电阻壁模在某一个位置继续增长（ωτw>>1）[172,173]；（2）通过外部线圈（共振磁扰动线圈或者校正场线圈）产生与外扭曲模反向的磁场减小或者消除外扭曲模[176-180]（见图9）。需要指出的是未来聚变堆基本都在低旋转下运行，因此两种方式中通过外部线圈控制电阻壁模将是主要的方式。由于在高比压下外加磁扰动幅值会被等离子体放大[146,175]，而这个效应目前也在误差场锁模中发现。总体而言，相对于误差场锁模物理，电阻壁模物理模型及参数依赖相对比较清晰。目前电阻壁模物理主要集中在一些细节及与其他物理过程结合方面[181-183]。电阻壁模的主要进展可以参考朱明盛2010 年的综述文章[184]。

图9 DIII-D 托卡马克上RWM 反馈控制下超过无壁比压极限下的放电时间演化[180]Fig.9 Time traces for discharges with βN exceeding the no-wall limit and RWM feedback using internal poloidal field sensors in DIIID[180]

4.3 种子磁岛的产生

由于在未来托卡马克运行的参数下，新经典撕裂模常常是稳定的，种子磁岛幅度的控制对于抑制磁岛生长具有重要的意义，因此可以将种子磁岛的产生单列出来。误差场驱动种子磁岛的最初想法来自于Hegna 在1999 年的驱动重联驱动种子磁岛的文章[185]，该文章内容的提出主要基于其于1998 年研究新经典撕裂模物理时注意到的初始稳定情况下(∆′<0)需要超过临界宽度的种子磁岛[186]。同年，Gude 等人在ASDEX Upgrade 装置上研究了锯齿坍塌或鱼骨模可以产生种子磁岛[187]。从图10 可以看出等离子体内部磁流体不稳定性可以作为误差场的来源直接诱发种子磁岛，诱发新经典撕裂模。从Callen 的综述中得到磁流体扰动强度一般为误差场的10 倍[145]，因此这个现象是比较合理的。2005 年，Pustovitov 考虑了外加共振磁场扰动可以产生种子磁岛，并注意到RMP 产生种子磁岛相对于磁流体不稳定性诱发种子磁岛需要的时间比较长[188]。2012年，虞清泉等人结合ASDEX Upgrade 装置参数通过约化磁流体和双流体模拟对误差场驱动种子磁岛进行了细致的研究[189]。这些研究对托卡马克装置等离子体三维真实位形下考察撕裂模有着积极的作用。

图10 锯齿坍塌诱发新经典撕裂模[187]Fig.10 Sawtooth crash induces NTM[187]

5 结论

本文从历史发展角度，梳理了误差场研究的历史与最新研究进展。作为托卡马克装置高质量经济运行过程中将要面对的重要科学问题，误差场锁模研究一直以来都是高参数运行重点关注的物理问题。为此，国际各大装置在物理设计阶段都对装置固有误差场会不会引起锁模问题开展了详细的物理分析并因此设计了结构复杂、数量众多的校正场线圈系统。未来聚变堆装置在物理设计阶段一旦不考虑装置固有误差场，将会造成装置运行在没有经济性的低参数区间，一旦想要跨过低参数区进入到高聚变增益阶段，则将遇到涉及到动态误差场校正、电阻壁模主动控制等一系列磁流体不稳定性行为。本文将误差场研究划分为三个发展阶段，给出了每个阶段大致研究热点及关注点。在早期阶段介绍了误差场研究的理论准备以及少量实验研究。在理论形成阶段，梳理出了四个主要理论流派，指出了各个流派的重要进展及对误差场锁模经典理论的贡献之处。从误差场锁模理论发展可以看出，国际上许多托卡马克知名理论学家都对误差场锁模理论进行了深入研究，这也从侧面反映出了锁模物理的重要性。在理论与实验结合阶段，国际上各大装置通过外加共振磁扰动开展了大量的误差场锁模实验研究，而与理论的详细比较及自洽性判断则由EAST 装置首先给出并经KSTAR 和DIII-D 后续验证。该阶段另一个重要突破就是误差场校正标准的重新认识和初步建立，然而后续研究还需要进一步确定该标准的适用范围以及是否需要进一步改进。在其他方面应用部分，简要介绍了外加共振磁扰动或者校正场线圈对边界局域模控制、电阻壁模动态控制以及与新经典撕裂模相关的种子磁岛的产生相关内容，并简要介绍了主要关注点及进展情况。

目前误差场锁模研究正处于全面突破的关键时期，其中最重要的就是阐明理论与实验在各种定标关系中的自洽性，这需要在国际托卡马克物理活动（ITPA）框架下开展各大装置间的协同研究。与此同时，理论上还需要进一步发展，在聚变堆相关的高参数运行区间给出清晰的物理规律。在此基础上，通过各个装置间的共同推进，进一步给出高参数下误差场锁模的物理规律。在理论与实验自洽性验证的基础上，便可以基于全面的理论定标外推，全面评估聚变堆误差场的容忍度，判断校正场线圈需求与否以及如何开展后续的动态校正。此外，未来研究还需要考虑聚变堆阿尔法粒子加热条件下的误差场锁模物理以及判断杂质等对误差场锁模的影响。

致谢

笔者在误差场方面研究工作的选题来自于导师王晓钢教授，谨以此文向王晓钢教授致以深深的敬意。感谢孙有文研究员和王正汹教授在研究中的指导与帮助，感谢万宝年院士和李建刚院士的指点，感谢中国科学院等离子体物理研究所诸多老师、同事以及其他国内外专家学者的指点。