基于可穿戴机械手臂参数估计与动力学模型分析

张江锋，吴志光

(池州职业技术学院 机电与汽车系，安徽 池州 247100)

人体的物理参数如惯性矩、摩擦度和肌肉力量等被应用于医学和运动学分析等研究领域，在估计人体物理参数的研究方面，Tsuji等人有一项关于人手的粘弹性特性和等效惯性的研究[1]。Nakamura等人也报道了无外部输入的物理参数估计[2]，通过安装在地板上的力传感器和动作捕捉来估计粘弹性、肌肉力等参数。然而，在许多关于粘弹性和肌肉力估计的研究中，惯性矩等参数的设置参考了样本和数学模型，因此忽略了个体差异。为了考虑个体差异，Kawamura和同事利用滤波和低摩擦机构估计了每个关节的惯性矩[3]。Gomi等人提前估计每个关节的惯性矩，探索粘弹性特性[4]。然而，这种方法很大程度依赖于测量设置，很难在实验环境中复制这些结果。目前对可穿戴机器人有广泛的研究，然而，利用可穿戴机器人对多关节惯性矩阵进行多输入估计的研究鲜有报道。

本文建立了人体手臂的动力学模型，并通过1个可穿戴的机器人手臂将输入应用到多个关节上，该机器人手臂上安装了编码器，每个关节上安装了驱动器。根据相关的输入和响应，对物理参数进行了估计。通过可穿戴的机器人手臂，可以将人的关节和机器人的关节紧密地放置在一起进行估计。

1 试验系统

1.1 人体手臂模型

本文中用于物理参数估计的人体模型如图1所示，其中，θ，l和m分别为关节角、连杆长度和连杆质心处质量。下标1、2和3分别与肩、肘和腕有关。该结构提供了3个平面弯曲自由度(DOF)，x轴和z轴分别表示正面和法线方向。

图1 链环模型

1.2 可穿戴机械臂

实验中所使用的可穿戴机械臂与1.1节中所述的模型相同。机器人手臂由3个驱动器(即肩、肘和手腕)组成，它们由编码器、齿轮和电机组成。实际安装的机器人手臂如图2所示。机械臂通过多条带固定在人臂上。连杆的长度可以根据受试者的身体大小进行调整，以匹配所有的关节角度。此外，由于既使用了编码器的位置信息，又使用了电机的位置信息，因此可以向机器人输入任意信号。通过计算相应的响应，可以估计出人臂的物理参数。

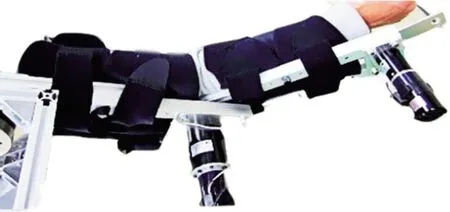
图2 可穿戴机器人手臂

2 动力学模型推导

本文推导了三关节动力学模型，利用拉格朗日方法[5]，得到考虑摩擦和重力的运动方程为

(1)

D=(D1,D2,D3)T，

(2)

C=(C1,C2,C3)T，

(3)

G=(G1sin(θ1)+G2sin(θ1+θ2)+G3sin(θ1+θ2+θ3),

G2sin(θ1+θ2)+G3sin(θ1+θ2+θ3),G3sin(θ1+θ2+θ3))T，

(4)

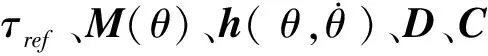
将式(1)中的已知和未知相加得

(5)

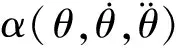
对于一个平面关节，β是由4个未知物理参数组成的1×4向量，具体计算式为

β=(M,D,C,G)T.

(6)

物理参数β由迭代最小二乘方法确定。进行了2种实验:一种是单独使用机械臂；另一种是固定在人体上的机械臂。利用估计的未知参数βrh,βr通过式(7)来推导βh，即

βh=βrh-βr，

(7)

式中：h为人臂；rh为固定在人臂上的机器臂；r为单独的机器臂。

3 输入信号和处理

在向人体输入信号进行人体参数的估计时，考虑到人体疲劳，应减少估计时间。本文通过同时进行多自由度估计，缩短了所有物理参数的估计时间。

3.1 输入设备

执行机构用带子或其他固定装置固定在身体的某一部分，当人的手臂放松时，可以估计物理参数。当该评估技术应用于同步多关节估计时，基于虚功原理，如式(8)所示，利用执行器的输入f和雅可比矩阵J，应用坐标变换输入τref到相应的关节，有

τref=JTf.

(8)

此时，需要为相应的接头考虑合适的输入信号,用τcom表示，实际应用的输入τref为

τref=JTJ-Tτcom，

(9)

式中：J是关节长度和关节角的函数。如果存在测量误差，则显示为J+δJ，出现输入误差，即

τref=(JT+δJT)J-Tτcom=τcom+δJTJ-Tτcom.

(10)

本文使用了一种可穿戴的机器人手臂，它的执行器布置在靠近人体关节的位置。用这种方法将输入应用到每个关节上，在估计上有2个优点：首先，与只对身体的一部分(如手指)进行输入相比，没有测量误差，估计误差可以减小；其次，每个关节的输入可以任意设置，以适应参数估计。

3.2 输入信号和参数估计

通过执行器输入的信号通常是具有良好信噪比的高功率信号，或保证PE条件的准白信号[6-7]。本文输入的二进制信号可以很容易地生成M序列的上述性质。

然而，对于由1和-1组成的二进制信号，图3(a)和3(b)所示的状态会相互交换。如图3所示，手臂上下两侧的带子通过旋转绷紧成肌肉，导致非线性振荡和相当大的能量耗散，影响了估计的准确性。为了解决这个问题，通过使用0和1的二进制信号将操作限制在一个单一的方向，这样肌肉总是被按在同一个方向。无输入如图3(c)所示，即使在没有任何输入的情况下，由于其自身的质量，带子也会一直收紧到手臂，因此肌肉变形总是达到一个极限。因此，可以在没有人-机器人耦合引起的非线性单元的情况下，可以在刚体模式下估计人手臂的动力学。该方法的弊端是，与(1，-1)二进制信号相比，功率会降低，可能会影响精度。关节角度对运动范围两端弹性单元的影响显著。本文忽略了末端区域，因此有必要对关节角度进行约束。

(a)正输入 (b)负输入 (c)无输入

约束：执行指定范围内(θmin<θ<θmax)的操作，其中θmin和θmax分别是最小和最大限制的角度范围，伸展手臂时，定义为0 rad.θlimit表示人的最大活动角度，当θmin和θmax分别设为θlimit/4和3θlimit/4，如图4所示。

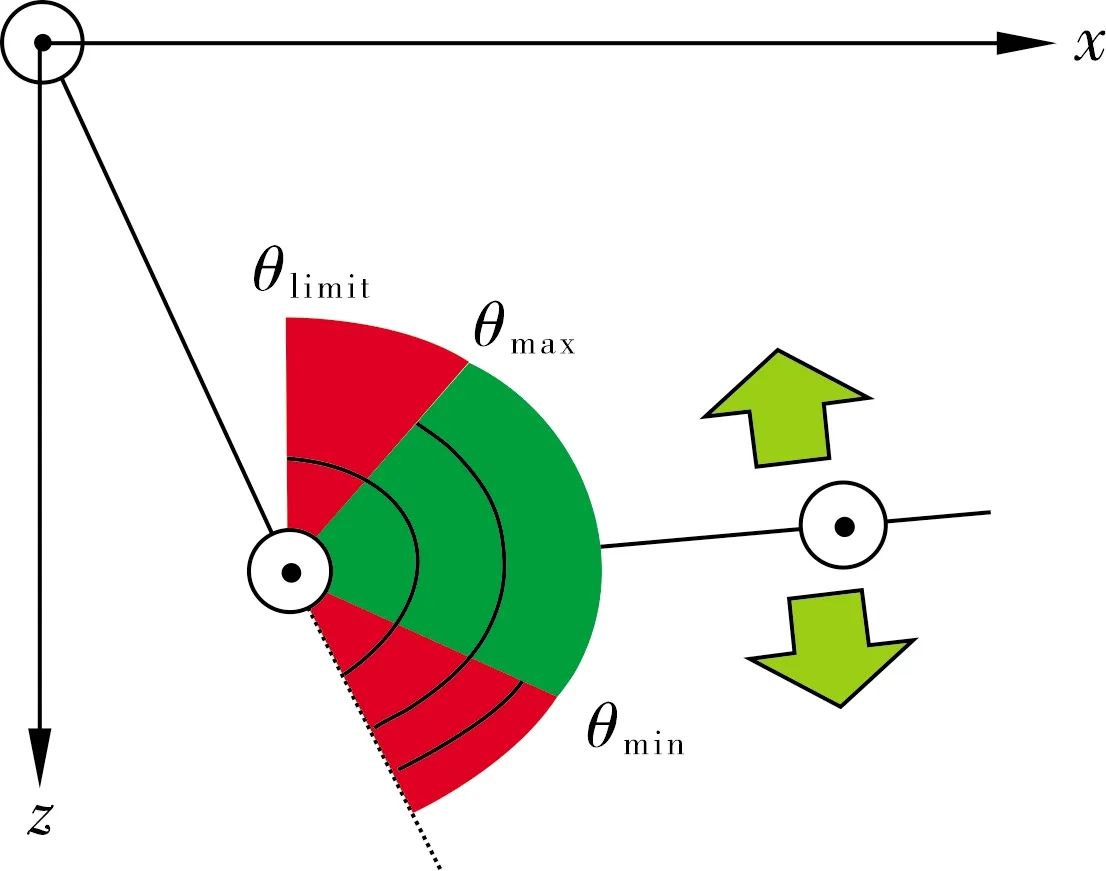
图4 运动和极限角度

当超过指定的范围时，将更改输入符号，并颠倒运动方向。此时，从信噪比的角度来看，二进制信号的振幅应对应最大扭矩。然而，在这种情况下，电动机转速接近ω=Nmax，转矩常数不再是线性的。这会导致错误。然而，如果振幅设置的小，避免接近ω=Nmax，输入被手臂的质量抵消，操作中途停止。因此，将二元信号与一个与时间成比例的变量t相加。需要注意的是，为了防止饱和，在反转操作时设置t= 0 s。由此可知，实际输入信号定义为式(11)，即

τref=At+BMseq

(11)

式中：A为与输入时间成比例的函数系数;B为二进制信号系数;Mseq为生成的二进制信号。具体参数见表1。

表1 实验参数

人体的物理参数估计使用输入信号τref和由编码器读取的θ。本文采用迭代最小二乘法来验证物理参数估计的收敛时间。

在实际的识别过程中，从θmin到θmax的时间约为0.5 s。因此，通过DFT分析了从t= 0 s到t= 0.512 s的肩关节输入，如图5所示。这里输入的直流分量很大，因为输入被应用，即使在重力影响下也可以适当的识别。另一方面，输入信号在其余频段几乎是恒定的，这意味着用于识别的输入信号是在宽频带内产生的。

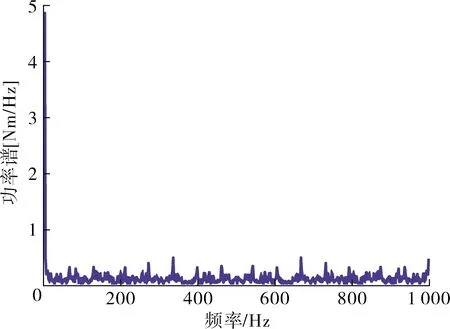
图5 输入谱

4 物理参数估计实验

4.1 实验概述

本实验包括分别对每个关节(肩、肘、腕)进行物理参数估计，以及同时对3个关节进行物理参数估计。首先，单独利用机械臂进行估计。实验重复50次以检验标准偏差。然后，用质量代替人的手臂来估计肘关节的物理参数，以确定固定带的效果。之后，用固定在人臂上的机械臂来估算物理参数，实验参数与表1相同，试验次数为50次。实验中，为防止温度变化引起估计值的变化，将室温保持在26 ℃。考虑到电机内部的温升，在实验前电机已充分预热。最后，为了验证估计值的准确性，比较了对固定在人臂上的机器人手臂的响应与使用估计值的仿真结果。

4.2 单关节估计

4.2.1 单独使用机械臂估计

浅色柱条表示已识别的机器人和人的参数值总和，深色柱条表示机器人的参数值，柱条之间的差异表示人的参数值。每个关节有4个未知的物理参数，3个关节共有12个未知常数。但是，在每个关节单独估计的情况下，不会估计干扰分量Ma、Mb和Mc。为了研究收敛时间，肩关节处的粘性摩擦项(收敛最慢)如图6(d)所示。

从图6(a)～(c)可以看出，(0，1)输入信号的功率减小导致的精度下降可以忽略不计。收敛时间约为1.5 s。

图6 单关节模型的识别结果

4.2.2 重量验证法

为了验证用于固定人类手臂的带子的效果，在机器人手臂上附加重量的情况下，估计了肘关节的物理参数。1 kg的质量放置在肘关节0.21 m处。在这种情况下，计算得到的惯性矩约为0.044 kg/m2，重力项增加约2.1 N·m。粘性摩擦和库仑摩擦不增加。估计结果如表2所示。

由表2计算的差值可以看出，惯性矩为0.046 kg/m2，重力项约为1.925 N·m，粘性摩擦为-0.0 023(N·ms)/rad，库仑摩擦为0.005 N·m。只有10%左右的误差出现在重力项上，这是由于机器人初始位置的误差。其他项的估计是准确的，表明波段的影响是微不足道的。

表2 附加质量的验证结果

4.2.3 对装在人体上的机械臂进行估计

对装在人体上机械臂的估计结果(平均值和标准差)在图6(a)～(c)中用深色柱条表示。收敛时间与图6(d)几乎相同，故忽略收敛时间。从图6(a)～(c)可以看出，除库仑摩擦外，其他各项的平均值均比单独使用机械臂时增大。这些增加值取决于人体手臂的物理参数。标准偏差也在增长，但没有相应的惯性、重力和粘性项的平均值那么大。因此，估计人体手臂参数是可行的。另一方面，在库仑摩擦的情况下，平均值的差异较小，其估计是困难的。这将在4.4节中解释，与其他参数相比，人体关节中的库仑摩擦较小，通常认为可以忽略。在实验中，机器人库仑摩擦的严重影响可能是导致估计失败的原因。

4.3 三关节估计

4.3.1 单独的机械臂

估计结果(平均值和标准差)在图7(a)～(c)中用深色柱条表示。肩关节粘性摩擦项的收敛时间(最慢的收敛)如图7(d)所示。

图7 三关节模型的识别结果

从图6(a)～(c)和图7(a)～(c)可以看出，相对于逐个情况(单关节估计)，三关机估计的标准差增大，Mra、Mrb、Mrc均为负值。这些应该是正的值和小的标准差。因此，我们认为稳态误差是由建模等因素引起的。

从图7(d)可以看出，收敛时间约为2.2 s。与图6(d)相比，每次试验的收敛时间增加了0.8 s左右。然而，分别估计每个关节的所有物理参数需要进行6次不同关节角度的试验，总共需要9.0 s。因此，同时进行三关节估计可以节省约6.8 s的时间。考虑到实验对象的疲劳，这种方法可减少估计时间，具有很大的优势。

4.3.2 对装在人体上的机械臂进行估计

估计结果(平均值和标准差)在图7(a)～(c)中用第1个柱条表示。收敛时间与图7(d)几乎相同，故省略收敛时间。从图7(a)～(c)可以看出，除库仑摩擦外，各项平均值均增大，与单关节估计相同。与单关节估计的值(图6(a)～(c))相比，标准差也增加了，但仍然可以以足够的精度估计人体手臂的物理参数。此外，Mrha、Mrhb、Mrhc增长，这表明机器人独有的值(Mra、Mrb、Mrc)存在稳定的误差。通过减法推导出人体物理参数，消除了这种稳态误差，认为人体物理参数不存在由这种稳态误差引起的误差。

4.4 估计验证

在模拟中使用估定值比较响应与逐步输入，在实验中使用机械手臂。图8中给出肩关节位置响应，虚线为仿真响应，其余10次为试验的实机响应。

除库仑摩擦外，模拟中采用4.2.3节的结果作为物理参数。这是因为当第4.2.3节库仑摩擦在其标准差范围内变化时，位置误差最小，接近第4.2.1节。从图8可以看出，从最大值和最小值得到的位置误差都在10%以下。由此得出结论，物理参数的估计具有较好的精度。

图8 模拟和实验肩部响应

人体手臂的库仑摩擦力太小，无法测量。从参数估计的角度来看，库仑摩擦是非线性的，可能会产生误差，在估计中单独处理可以提高精度。模拟结果表明，在不考虑库仑摩擦的情况下，实际物理参数的估计标准差减小。

5 结语

本文利用可穿戴机械臂在人体关节附近布置驱动器，提出了一种估计人体手臂物理参数的方法，可以在没有人机耦合引起的非线性单元的刚体模式下估计动态特性。实验分为2组：分别估计每个关节(一个接一个)的物理参数；同时估计3个关节的物理参数。在估计包括干涉项在内的所有物理参数时，同时进行三关节估计的速度要快6.8 s左右。考虑到人的疲劳，减少估计时间是一个很大的优势。将仿真结果与实验结果进行对比，验证了所提方法精度较高，位置误差在10%以下，性能较优越，首次实现了惯性矩阵非对角元的估计。