模糊C均值结合神经网络的短期电力负荷预测*

王 瑞， 杨炜炜，逯 静

(1.河南理工大学 电气工程与自动化学院,河南 焦作 454000;2.河南理工大学 计算机科学与技术学院,河南 焦作 454000)

0 引 言

随着社会的发展，人工神经网络受到了国内外学者的青睐。最速梯度下降法是人工神经网络中修正参数较常用的算法之一，但其很容易陷入局部极小点无法逃脱。近年来，粒子群优化(PSO)算法、遗传算法(GA)、模拟退火(SA)算法等应用到神经网络的优化，并取得较好的预测效果[1～3]。在实际预测中大多数预测模型都是建立单一预测模型进行预测，而对于复杂的电力系统可以采用多个模型组合组成新的模型[4,5]进行负荷预测。文献[6]对地区负荷进行行业聚类，分析影响用电特性的主要因素,建立相关聚类、关联模型进行预测。文献[7]提出了一种模糊膜聚类算法与改进极限学习机相结合的组合预测方法。文献[8]提出基于硬C均值(C-means)聚类算法建立神经网络进行电力系统短期负荷预测并取得了较好的预测效果。

考虑到负荷的周期性等特点，本文应用C均值聚类的基本原理，采用同类(聚类分析后)特征数据作为预测输入。将模糊C均值(fuzzy C-means,FCM)聚类算法和改进的RBF神经网络结合建立预测模型进行预测。 应用引入模拟退火思想的粒子群优化(simulated annealing particle swarm optimization,SA-PSO)算法来改善径向基函数(radial basis function,RBF)神经网络陷入局部极小值的缺陷。

1 RBF神经网络

RBF神经网络是与BP神经网络结构相似、收敛速度更快的一种可以逼近任意非线性函数的神经网络。RBF神经网络(多输入单输出)输出可描述为隐含层节点的线性组合

(1)

式中y为神经网络的输出；M为隐含层神经元的个数；wi为第i个隐含层神经元与输出神经元的连接权值，(i=1,2…m)。qi为第i个隐含层神经元的输出(本文采用最常用的高斯函数)，即

(2)

式中X=[x1,x2…,xl]T为输入向量，l为向量维数，ci为高斯函数的中心；σ为高斯函数的方差；‖X-ci‖为欧氏范数。

RBF神经网络训练的过程就是对神经网络不断调整参数和权值使样本集总误差尽可能小过程,即

(3)

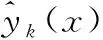
2 算法描述

2.1 FCM聚类

FCM算法最早由Dunu J[9]提出，Bezdek等人进行了完善和推广。根据样本集的特性指标进行聚类分析，聚类后的数据即构成了分类。设样本为X=[x1,x2…,xl]，聚类数为C，建立目标函数

(4)

式中uik为第k个样本在第i类中的隶属度；zi为第i类的中心；dik为第k个样本到第i类的中心距离

(5)

(6)

m为隶属度的加权函数。其流程为：

Step1 给定初始参数m，一般取2。给定停止阈值δ以及迭代计数器b=0，初始化聚类中心。

Step2 利用式(5)、式(6)不断修正。

Step3 如果使得‖Ul+1-Ul‖<δ，则停止输出划分矩阵和聚类中心；否则，令b=b+1，转向步骤Step2。

Step4 按式(7)逐一计算待预测日的特征矢量与各聚类中心的欧氏距离

(7)

以欧氏距离最短的类别作为待预测的类别选合适的样本建立RBF神经网络进行预测。

2.2 SA-PSO算法

PSO算法是由Kennedy等人提出来的一种群体智能算法。文献[10]已给出标准的PSO算法综述，这里不再详细论述。为了描述方便，简单介绍下标准PSO算法中粒子的更新。

粒子更新自身速度的公式为

(8)

粒子更新自身位置公式为

(9)

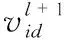
SA算法最早由Metropolis等人提出的，模拟固体更新退火冷却过程的行为。SA的基本思想为从一定的解开始，从邻域中随机产生另一个解，接受准则允许目标函数在一定范围内变坏并且以一定的概率[11]。

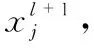
(10)

式中η为扰动的参数，ε为服从正态分布的随机变量。

Step1 初始化各个参数；

Step2 判断是否满足停止条件，若满足转到Step7，若不满足执行Step3-Step6；

Step3 计算每个粒子适应度值；

Step4 按式(8)、式(9)更新pbestid和gbestd；

Step6 按照粒子群更新公式对粒子群的速度和位置进行更新；

Step7 输出最优结果。

2.3 SA-PSO-RBF神经网络

梯度下降法是最常用的求解神经网络参数方法之一，理论上其训练是沿着误差曲面的斜面向下逼近的。而对于一个复杂的网络而言，分布着许多局部极小点。在训练过程中，一旦陷人了这样的局部极小点将无法逃脱。针对这问题，本文采用SA-PSO算法来代替梯度下降法来修正网络参数。利用SA-PSO算法强大的全局搜索能力，使得训练过程有机会跳出局部极小点得到全局最优解。SA-PSO算法改进RBF的流程图如图1。

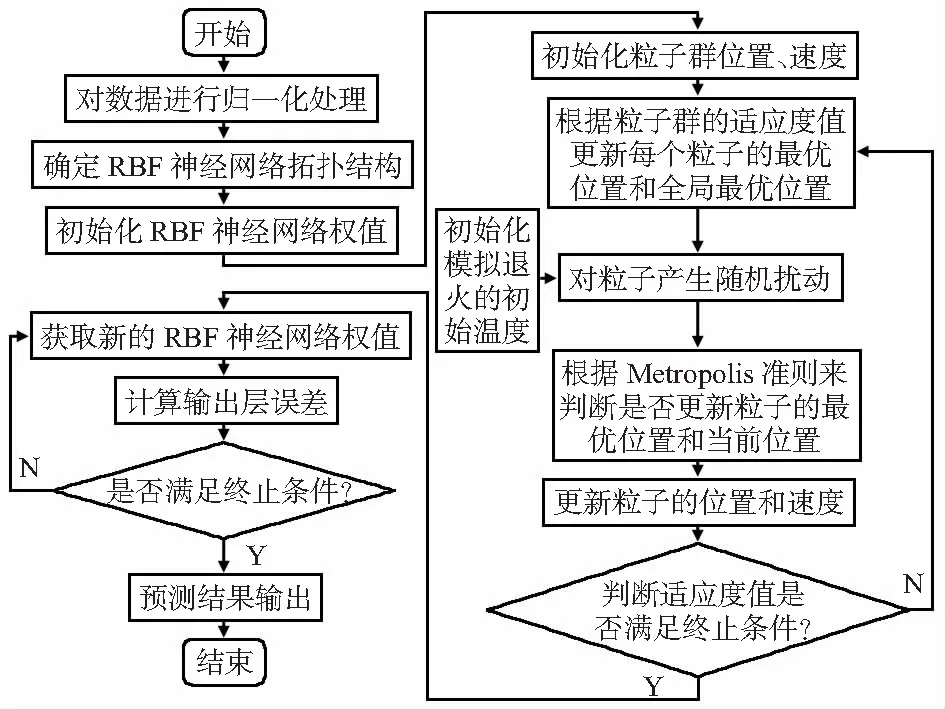
图1 SA-PSO-RBF神经网络算法流程

3 FCM聚类结合神经网络预测模型

根据聚类的状态特征选一批日类型、气象条件、温度与预测日相近的数据作为SA-PSO-RBF神经网络的预测输入。本文提出的应用FCM聚类的预测模型,其模型图如图2所示。

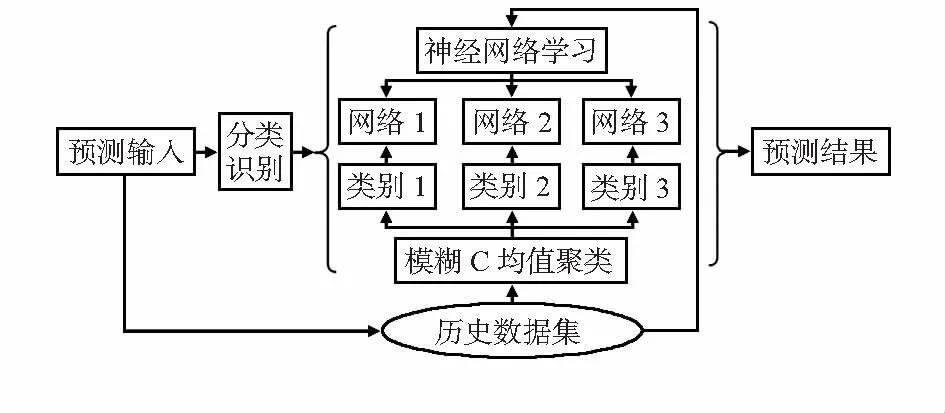
图2 FCM结合神经网络的流程

综合考虑负荷数据、天气、日类型、温度等影响负荷的主要因素，将历史数据库的预测样本数据分成若干类别，对预测日进行预测时。首先通过式(7)识别找出与预测数据相似的类别，并用对应类别已经训练好的SA-PSO-RBF神经网络进行短期的负荷预测。

4 电力系统短期负荷实例分析

从河南某县电力公司采集2018年5～7月的负荷数据并进行预测。图3为该县5月8～9日的负荷变化图。

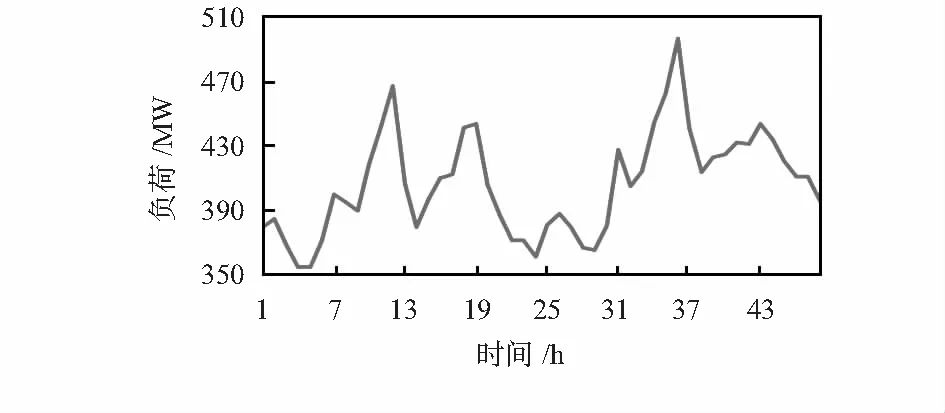
图3 5月8日至9日负荷变化

从图3中可以看出:两天的负荷大小有所不同，但变化趋势基本相同，一天内负荷呈现周期性变化。

4.1 数据的规格化

在特性指标中，各指标的数量级和量纲之间存在差异，可以通过归一化的方法除数量级和量纲之间差异带来的影响。对于温度、工作日类型等的描述不能直接作为神经网络的输入，需要进行量化处理。其映射关系见表1。

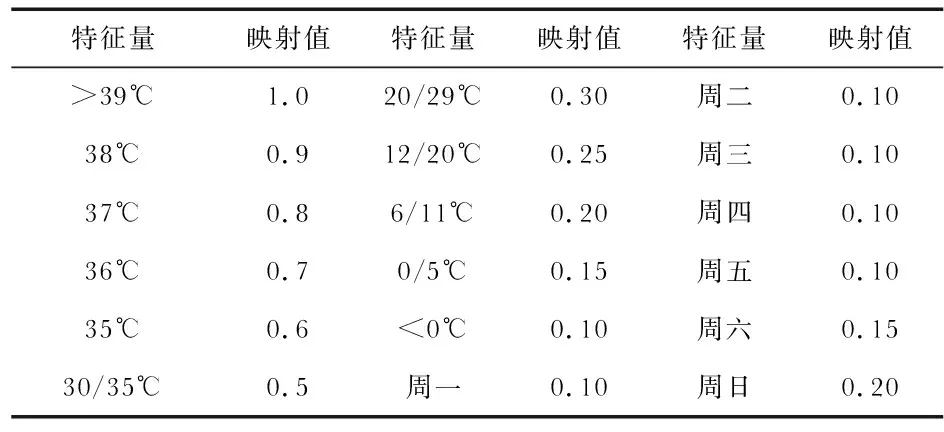
表1 特征量映射表

4.2 对负荷数据的处理

进行预测前先对负荷数据进行归一化处理，公式如下

(11)

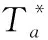
4.3 神经网络输入层与输出层的确定

神经网络节点描述如表2所示。

表2 神经网络输入输出对应表

4.4 预测性能指标

预测性能指标有三种，分别为最大绝对误差(maximum absolute error,MAXAE)、平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE)三种类型公式如下

(12)

(13)

(14)

式中y′为负荷值的预测值，y为实际负荷值。

5 实验分析

为了验证提出的FCM结合神经网络的预测模型预测的实效性。对河南某县2018年5～7月的负荷数据进行FCM聚类。本文设置C为8，取δ=0.01。在 MATLAB平台上进行实验仿真，用单一的RBF神经网络预测模型、SA-PSO神经网络预测模型作为对组照组。三组预测结果如图4所示，预测误差对比图如图5所示。

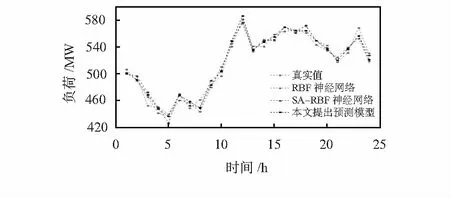
图4 各模型预测对比

图5 预测误差对比

由图4可知，三种模型在负荷预测中都能有较好的效果。从图5可以看出,本文提出的预测模型预测误差更小,预测效果比单一的RBF神经网络和SA-PSO-RBF神经网络要好。

在表3中，从MAXAE，MAE，MRE三种预测性能指标看出,第三组预测模型相有明显的降低,证明该预测方法准确度更高。

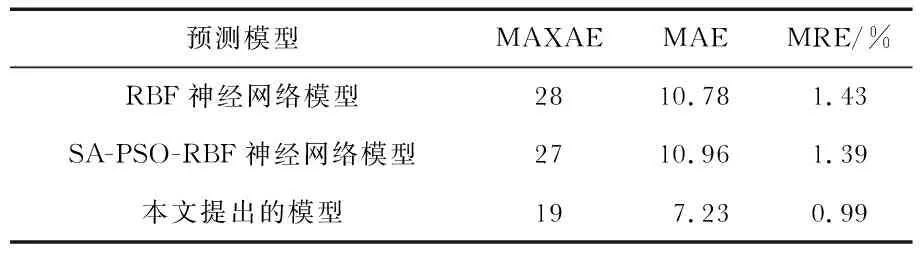
表3 模型预测结果

6 结 论

本文在对RBF神经网络分析的基础上，采用FCM聚类进行数据处理。充分考虑了样本空间的特征并进行分类。选取与预测日相似度高的作为神经网络的输入，对预测日进行预测。使得模型具有针对性，可以进行可靠的预测。

构建的SA-PSO-RBF神经网络在保证了PSO算法简单易实现的这一优点的基础上，增强了粒子的全局寻优能力，加快算法运算速度。通过实验仿真结果证明预测模型的预测结果误差精度提高，取得了较好的预测效果。