V沟槽圆柱后流流动特性

晏 飞，王德强

（江苏科技大学 机械工程学院，江苏镇江 212003）

0 引言

圆柱形结构广泛应用于流体机械和海洋工程中，其应用包括导管架、自升式平台和海洋装腿机械结构、海洋管道和海洋立管。海洋装腿机械结构和海洋立管在海水中，支撑海洋着平台，受海水流动作用的影响容易产生涡激振动。而涡激振动对海洋装腿机械结构和海洋立管的危害，会导致安全隐患，降低其使用寿命。因此，为了抑制涡激振动，延长机械设备的使用寿命，对圆柱绕流的流场研究是非常必要的，并且现在已经将研究重点放在涡激振动（VIV）的抑制上。

涡激振动的抑制可以从两方面出发：（1）避开结构的固有频率，使结构物在绕流过程中始终处于低幅值振动，不会发生共振；（2）抑制漩涡的形成和发展，从源头上解决问题［1-3］。本文对涡激振动的研究主要集中在抑制漩涡的生成和发展。

目前，关于圆柱绕流以及改变圆柱体表面结构以减小阻力和涡流引起的结构振动的研究较多。黎润恒等［4］用大涡模拟（LES）对光滑圆管和三角形沟槽面圆管的流场进行数值研究，结果表明：三角形沟槽面圆管的摩擦阻力均小于光滑圆管，说明这种形式的沟槽在圆管湍流中具有很好的减阻效果。王伟等［5］采用非定常数值计算方法，在圆柱表面布置4组脊状结构物，研究沟槽结构对圆柱绕流流体特性的影响，结果表明在布置4组脊状结构物时可以有效减小圆柱的阻力，阻力系数最大减少32.56%。王珺等［6］对安装在水泵叶片全翼面和前，中，后3个不同位置处加装6种不同粗糙度的V型结构进行了数值模拟，并研究了V型槽在水泵叶片上的减阻效果，结果表明：V型槽结构布置在整个叶片上没有减阻作用；当V型结构粗糙度为1/15 00且布置在翼型后段时，减阻效果最好，最大减阻率可达7.4%。以上研究均未对V沟槽的深度进行深入研究，不同的V沟槽深度也可能对减阻特性产生影响。基于此，本文主要研究不同深度的V沟槽圆柱对减阻特性的影响。

正交分解是分析复杂流动现象的一种有效方法，因此它可用于分析钝体后的复杂的漩涡脱落现象。MA等［7-8］将POD技术应用到圆柱绕流分析中，并直观地观察了圆柱尾迹上的漩涡脱落规律。因此，POD可以用于提取流场的主要特征。

本文采用粒子图像测速（PIV）技术和正交分解（POD）方法对不同深度V沟槽圆柱尾流的流场速度和流动特性进行测量和分析，从POD模态能量分布、POD模态系数、基于POD模态系数的相关性等方面研究不同深度V沟槽圆柱的流场变化。

1 试验装置

如图1所示，试验在PIV粒子试验室的循环水槽中进行。在试验过程中，通过PLC控制水流速度；流量计记录每次试验的流量，然后根据水槽的横截面面积和流量计的流量，计算出试验段的水流速度，即：Q=SV0（其中流量Q=180 m3/h，S为截面积，V0为试验中的流速）。试验段具体尺寸截面为0.3 m×0.45 m（宽×高），长约1 m，壁厚0.01 m。此外，循环水槽的前后表面均采用无色有机玻璃，便于光学设备产生的激光进入，以及PIV测量的视觉评估。

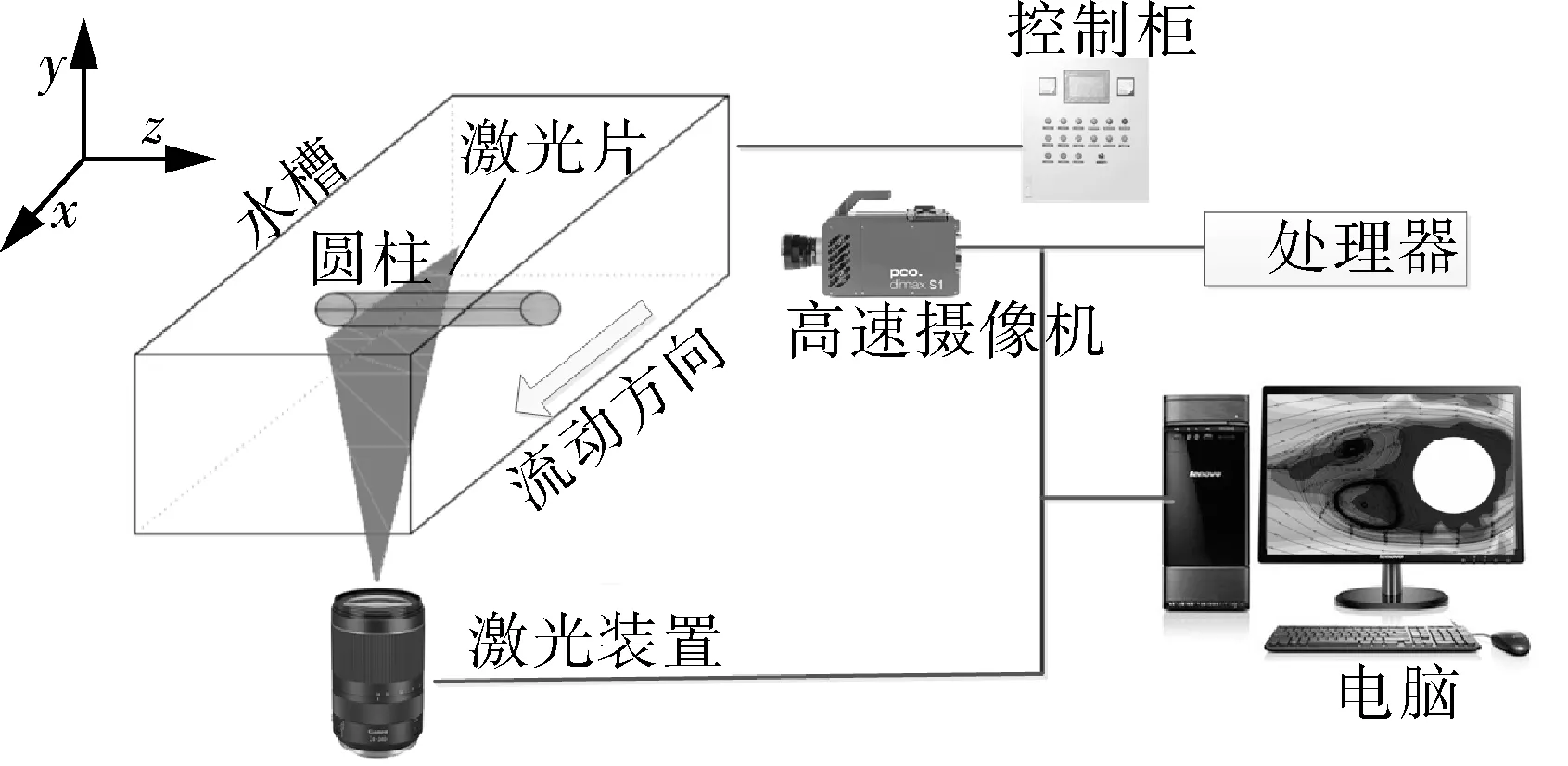
图1 PIV粒子循环水槽试验系统Fig.1 PIV particle circulating tank experiment system

试验中使用的圆柱体是由PVC材料制成的，其长度L=300 mm，直径D=20 mm。当沟槽角度为60°、沟槽数量为16个时，V沟槽具有较好的减阻效果。所以本文在此基础上选择继续探究不同深度对减阻效果的影响。如图2所示，在圆柱横截面上等角度均匀分布16个V沟槽，其沟槽角度均为60°，沟槽深度k分别为0，1，2，3 mm（粗糙度系数k/D分别为0，0.05，0.1和0.15），其对应的标记为方案1～4。在此基础上对圆柱进行V沟槽加工，保证加工尺寸的精度。

图2 圆柱体截面示意Fig.2 The schematic diagram of the cylinder cross-sections

圆柱体的长径比L/D为15，这种长径比被认为足够大，以保证圆柱近尾迹的二维流动［9］。如图3所示，试验段水面的高度距离圆柱225 mm，圆柱安装在水槽高度的中间位置。二维平面的原点位于圆柱体的基部并沿着中间平面指向水流方向，坐标x，y，z分别表示流向、横向和展向。试验中自由流速度为0.37 m/s，对应Re=7.4×103。V沟槽深度分别为0，1，2，3 mm。

图3 试验圆柱的放置位置Fig.3 Positions of the experimental cylinders

PIV技术用来获取流场数据，这是用POD方法分析流场的关键步骤。如图1所示，PIV技术采用激光照射试验平面上，通过示踪粒子的运动间接反应流场的运动，示踪剂颗粒直径为10 um，可以很好地满足流场分析的需要。同时，PIV系统采用了高速摄像机，高速摄像机（pco.dimax S1）的典型分辨率为1 008×1 008 像素，并且以1 ms（即每秒1 000帧）的时间间隔连续捕获2 000幅数字粒子图像，连续两个图像之间的快门速度被设定为每一帧1.5 μs。图像处理系统基于傅里叶变换对图像进行处理，从而获得整个流体区域的流动信息。

2 POD公式

POD方法的本质问题是在函数空间中找到一组“最优”的正交基，这里“最优”是指将函数空间投影到正交基上所造成的误差最小化［10］，定义一组样本的平均速度场和脉动量为：

式中U（x，y）——平均速度场；

u'（x，y，ti）——脉动量。

POD方法将脉动量u'（x，y，ti）分解为空间模态φi（x，y）和时间系数ai（t）。

即：

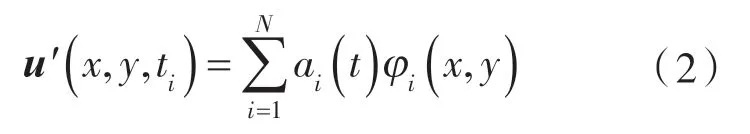
式中 a（it）——第i阶模态的时间系数；

φ（ix，y）——特征向量。

实际上，求解空间模态等价于求解以下最大值问题：

式中 （φ，φ）——L2（Ω）的内积；

——内积空间（Ω）的范数。

这里引用了快照POD方法［11］来表示特征模态。具体过程如下：对于N个快照的二维速度场u'（x，y，ti），时空速度场的脉动量有这样的形式u'（x，y，ti）=（u'，v'）。一个矩阵U'可以用来描述流场的所有速度脉动信息，即：

式中 l，m —— 流 场u'（x，y，ti）在x，y方 向 上 的节点数；

N ——时间上的样本总数，N=2 000。

从而得到矩阵C：

POD分析的目的是用来分解流场数据，通过快照法求解特征向量Ai和特征值λi。

从上式中可以求得特征值λi和特征向量Ai，根据特征值λi的大小进行排序，λ1＞λ2＞…＞λN=0，相应的特征值也表示每个模态所包含的能量大小，而每个特征值与所有特征值之和的比，反应了模态中包含的信息对流场的贡献程度。流场的总能量可以表示为所有特征值λi之和，即：因此，各模态所占总能量的百分比被描述为：Ei=λi/E，它表示第i阶POD模态φi所包含的“能量”。此外，POD模态φi的方程为：

得到模态矩阵Φ：Φ=［φ1，φ2，…，φN］，而POD模态系数ai对应第n阶快照，即：ai=φiu'n。根据POD系数ai和对应的模态φi重构二维速度流场，可以得到：

更详细的快照POD方法可以参考SIROVICH等［9］的研究

3 结果与讨论

3.1 V沟槽结构表面流场的结果

图4示出了漩涡特征及其参数，可以描述近尾迹再循环区域。图中LR表示再循环区的长度，该长度是从圆柱体中心沿流动方向测量；a表示圆柱中心与漩涡中心之间的距离；b表示2个旋涡中心之间的距离［9，12］。

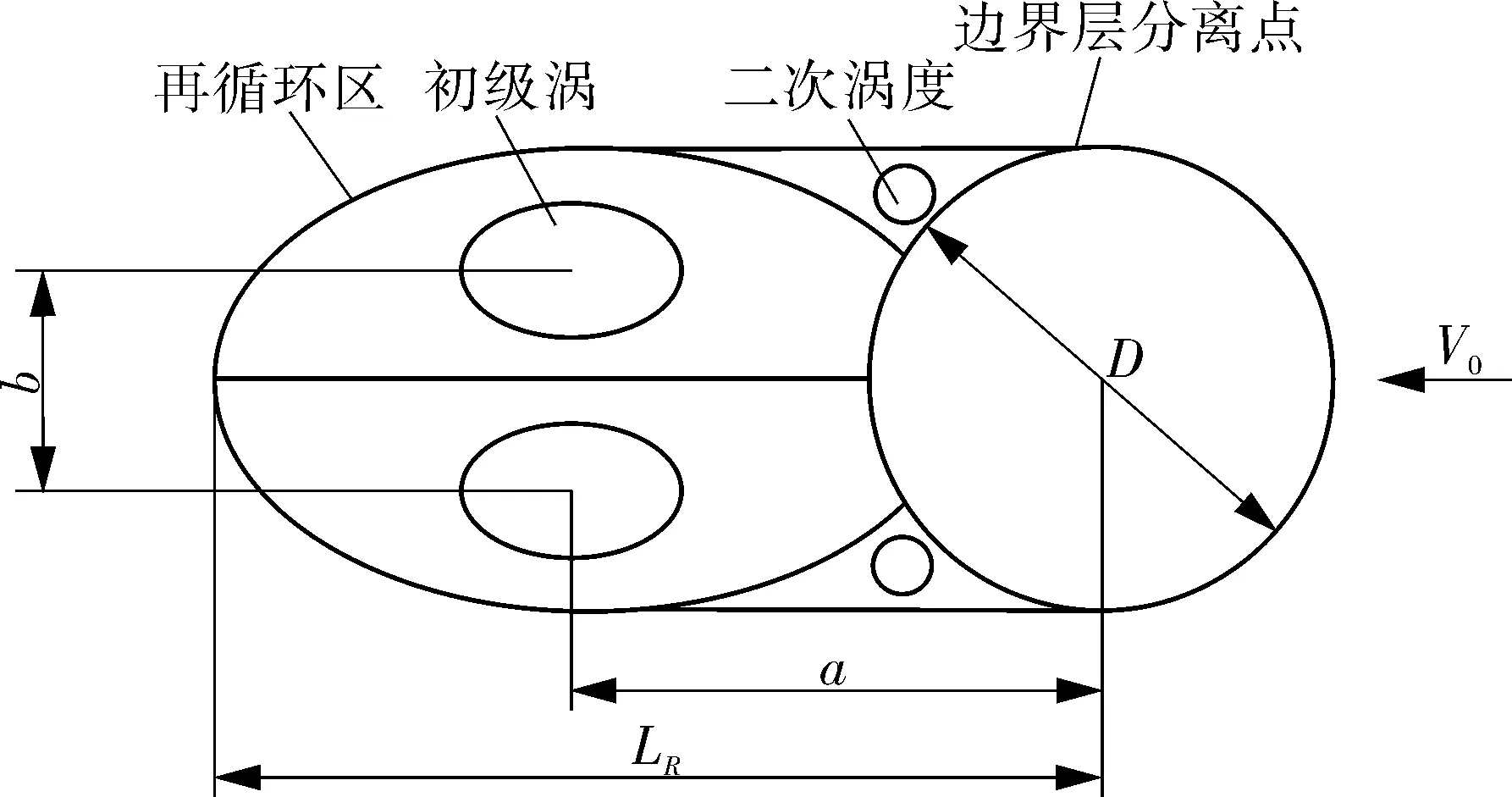
图4 再循环区域示意Fig.4 Schematic diagram of the recirculation region

图5 示出了流线型模式和时间平均速度矢量分布。可以看出，方案2～4的a和LR比方案1的长，同时方案2～4的a和LR依次递增。由此可以得出结论：光滑圆柱的再循环区比表面带有V沟槽的圆柱的再循环区要小，这意味着V沟槽的结构和深度会影响旋涡尺度。此外，仔细观察发现，表面带有V沟槽的圆柱的回流区纵向延伸略大于光滑圆柱的回流区，这可能是由于分离角增大所致［13-14］。

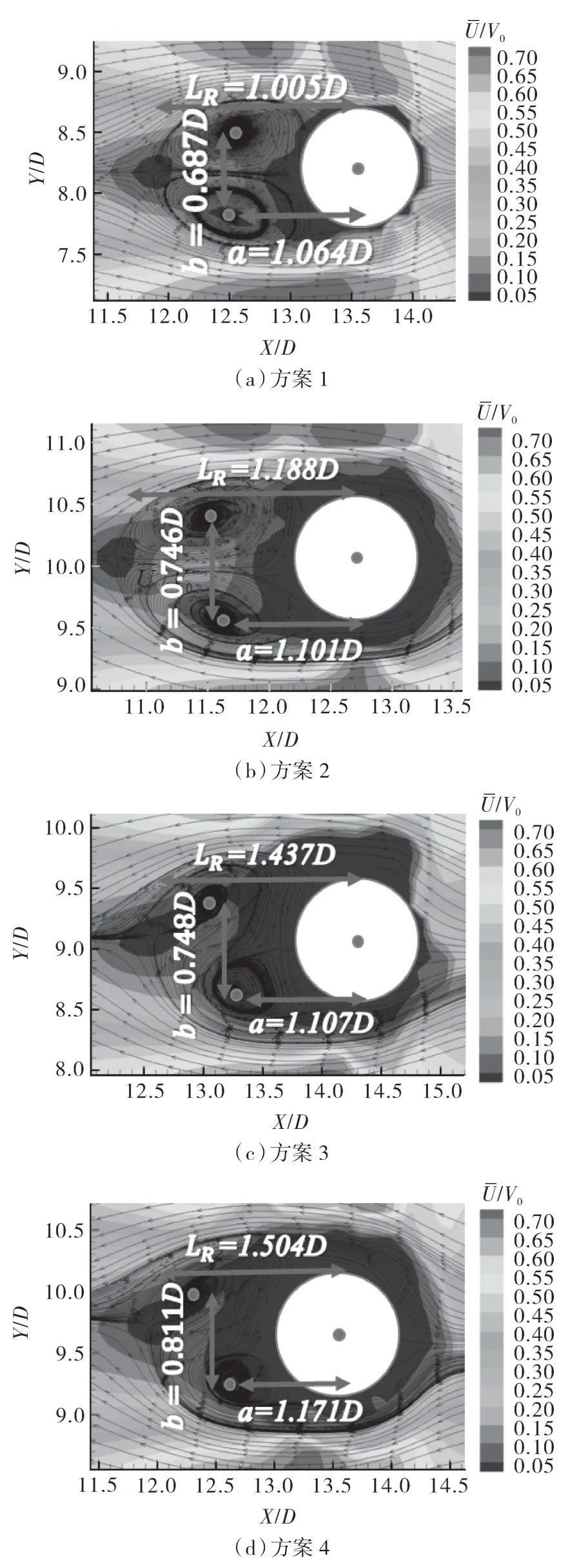
图5 试验圆柱后尾流的流线形态和时间平均速度Fig.5 The streamline patterns and time-averaged velocity of the wake flow behind the experimental cylinders

图6 ，7示出了速度脉动分量u'（u'=urms/［V0的 速 度脉动强度（urms/V0和vrms/V0）。如图6所示，光滑圆柱（case 1）近尾流区的流向速度脉动的峰值强度约为urms/V0=0.45，而在表面带有V沟槽的圆柱（方案2～4）中，该峰值强度降低到约0.42～0.35。此外，与方案1相比，方案2～4的峰值出现时间有所延迟。出现上述现象可能是由于剪切层漩涡生长缓慢，持续时间短造成的［14］。

图6 速度脉动分量u'的流向速度脉动强度Fig.6 The streamline velocity fluctuating intensity of the velocity fluctuating components u'

横向速度脉动强度的分布如图7所示。与光滑圆柱（方案1）相比，表面带有V沟槽圆柱（方案2～4）的横向速度脉动峰值强度出现的位置延迟了，方案2和方案4延迟了0.5D，方案3延迟了1D，并且峰值区域都受到很大限制。此外，光滑圆柱的峰值横向速度脉动强度大于表面带V沟槽的圆柱。峰值横向速度脉动强度的位置、大小的显著差异证明了表面带有V沟槽圆柱近尾迹中的漩涡脱落过程受到抑制。综上所述，V沟槽结构削弱，剪切层漩涡的增长速度，并延迟卡门涡街的形成，所以导致了再循环区增大［14］，如图7（b）～（d）所示。

图7 速度脉动分量v'的横向速度脉动强度Fig.7 The transverse velocity fluctuating intensity of the velocity fluctuating components v'

3.2 POD模态的能量分布

图8 示出了光滑圆柱和表面带有V沟槽的圆柱的POD模态能量分布（图中Ei表示不同POD模数的能量所占比例）。从图中可以清楚地看到，能量主要集中在模态1和模态2中，因此模态1和2对流场总波动能量的贡献最大。随着POD模数的增加，POD模态对应的能量迅速减少，并逐渐趋于零，说明POD模态的能量分布具有明显的收敛性［13，15-16］。

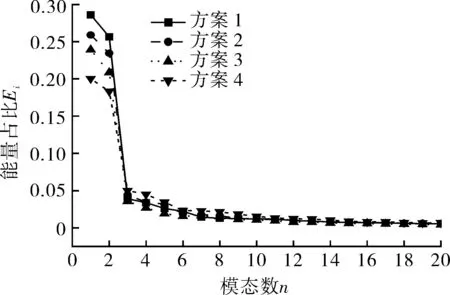
图8 POD模态所包含的能量Fig.8 The energy contained by POD modes

如图8所示，方案1中的模态1和2占总波动能量的54.28%，随着V沟槽深度的增加，方案2～4中模态1和模态2的能量占比依次减小，分别达到总能量的49.37%，44.80%和38.38%，由此可知：模态1和模态2的能量占比减小可能是由于V沟槽结构对边界层的影响，从而导致漩涡脱落减弱，涡街的形成延迟［13，17］。

3.3 POD模态系数

图9示出了a1（t）在整个流动时间内的分布。从图可见，对于方案1来说，a1（t）具有比较完整的正余弦周期，其周期对应漩涡的形成和脱落过程。而对于方案2～4，其周期性被打破。另一方面，随着流动时间的增加，方案2～4的a1（t）峰值均小于方案1，并且方案2～4的a1（t）的峰值各不同，这反应了V沟槽的深度对峰值的影响，这也是光滑圆柱的再循环区小于V沟槽圆柱的原因之一（如图5所示）。

图9 POD模态系数（模态1）随时间变化的分布Fig.9 The distribution of POD mode coefficient（mode 1）with time

3.4 POD模态系数的相关性

通过观察POD模态系数的相关性，可以了解流动的精细结构，以及涡流释放宏观改善的原因［18］，因此，对于复杂的流场，POD模态系数的相关性是值得研究的课题。

在进行相关分析之前，对POD模态系数ai（t）进行归一化处理，即：

如图10所示，a1（t）与a2（t）的相关性清楚地表明了a1*和a2*之间的耦合关系。

图10 POD模态系数（模态1和模态2）的相关性Fig.10 The correlation of POD mode coefficients（mode 1 and mode 2）

从方案1可以看出，a1*和a2*的相关性与准圆形有关，其结果可能是由小尺度的波动或湍流引起的［19-22］，同时也说明了模态1和模态2的系数耦合更好，漩涡脱落更有规律性。在方案2～4中，a1*和a2*的相关性与准圆形无关，这意味着在一定程度上V沟槽结构抑制了旋涡的脱落，从而导致了a1*和a2*的耦合被打乱。此外，随着V沟槽深度的增加，数据点的分布越来越无序，反应了V沟槽的深度对耦合结果的影响。

4 结论

（1）表面带有V沟槽圆柱的再循环区（LR分别为1.188D，1.437D，1.504D）大于光滑圆柱的再循环区（LR=1.005D），V沟槽圆柱的再循环区分别延长了0.183D，0.432D，0.499D，特别是V沟槽深度最大的圆柱的再循环区。

（2）在流场中，能量集中在模态1和2中。光滑圆柱的模态1和2能量占比为55.56%，3种V沟槽圆柱的模态1和2能量占比分别为44.85%，28.84%和25.58%，说明表面带有V沟槽圆柱的模态1和2所含能量比光滑圆柱少，这意味着V沟槽结构能够减缓漩涡脱落过程和延迟涡街的形成。

（3）光滑圆柱的POD模态系数与准圆形有关，表明模态1和2的系数耦合较好。然而这一特征受到V沟槽结构的干扰，导致耦合变弱，并且随着槽深度的增加，耦合进一步变弱。