再生混凝土的单轴压缩动态力学性能

白卫峰， 李思蕾， 管俊峰，*， 郑永杰， 苑晨阳

（1.华北水利水电大学水利学院，河南 郑州 450046；2.中国电建集团西北勘测设计研究院有限公司，陕西 西安 710065；3.中国建筑第七工程局有限公司，河南 郑州 450004）

混凝土是典型的率敏感性材料，其力学性能受加载速率的影响比较显著［1‑3］.率相关行为与混凝土基体内部微裂纹的形成过程有着密切的联系［4‑5］.对于再生骨料混凝土（RAC，简称再生混凝土），由于再生骨料表面同时存在新旧水泥砂浆2 种界面过渡区及更多的微缺陷，导致再生混凝土表现出的应变速率敏感性特征更为复杂.

肖建庄等［6‑7］研究发现，再生混凝土存在显著的应变率敏感性特征.Wang 等［8‑9］研究发现，在较高的应变速率下大量再生骨料被一些裂缝穿透，再生混凝土相比普通混凝土表现出更大的应变率敏感性.李龙等［10］研究发现，再生混凝土的峰值应力和弹性模量随着应变速率的增大近乎线性增大，且不同取代率下再生混凝土的动态抗压强度提高幅度均大于普通混凝土.有些学者得出相反的结论，如文献［11］显示对于普通混凝土和再生混凝土，应变速率为10-2s-1时的抗压强度，相比应变速率为10-5s-1时的抗压强度分别提高了27.84%和20.76%，再生混凝土的动态强度增长因子低于普通混凝土.崔云璇等［12］和Xiao 等［7］分别开展了再生混凝土的动态力学试验，研究了应变速率对再生混凝土弹性模量、抗压强度、变形能力和破坏模式等的影响规律.

目前文献中关于再生混凝土动态力学性能的试验研究相对较少，且结论存在一定的差异.同时由于试验技术的限制，对再生混凝土动态力学性能的研究多集中在宏观力学性能方面，针对细观损伤机制的研究较少.建立的本构模型大多是宏观唯象的，无法在细观机制与宏观本构行为之间建立起有效的联系.

混凝土等准脆性材料的变形破坏实质上是内部微裂纹、微孔洞等微缺陷的成核、萌生、扩展的连续损伤演化过程，涉及宏、细、微观多个尺度上无序非均匀性的跨尺度耦合［13］.细观统计损伤力学的发展，为人们重新认识混凝土等准脆性固体材料的变形破坏过程提供了新的研究方法和工具［14‑18］，通过定义能够描述由大量微损伤组成的系统概率分布函数并确定其统计演化方程，提供了连接细观损伤机制与宏观非线性本构行为之间联系的桥梁.

本文以C30 普通混凝土配合比为基准制备再生混凝土，开展再生混凝土的单轴压缩动态力学性能试验，研究再生混凝土的动态力学性能及宏观变形破坏特征；同时结合细观统计损伤理论，分析应变速率对再生混凝土单轴压缩过程细观损伤机制的影响规律，比较再生混凝土和普通混凝土动态力学性能的差异.

1 混凝土统计损伤理论

1.1 基本假定

混凝土是由多相介质组成的复合材料，变形破坏过程中微结构内部存在2 种作用机制［19］（见图1）：（1）劣化效应.受力过程中，在骨料和水泥砂浆交界面等薄弱部位会由于局部拉应变超过限值而导致微裂纹的萌生和扩展，期间伴随着声发射等能量耗散现象.（2）强化效应.伴随着微裂纹的萌生和扩展，微结构应力重分布得以实现.薄弱部位陆续退出受力，有效受力骨架得以进一步优化调整，从而能够承受更大的外界荷载.

图1 微结构的劣化和强化Fig.1 Deterioration and strengthening in microstructure

1.2 单轴压缩

1.2.1 细观损伤机制

图2为单轴压缩示意图.如图2所示，在单轴压缩过程中，混凝土的宏观变形破坏特征、应力-应变行为与细观损伤机制密切相关.整个过程分为2个阶段，即分布损伤阶段和局部破坏阶段.图2（b）显示了混凝土典型的名义应力-应变曲线和预测的有效应力-应变曲线.压缩方向记为3方向，对应名义应力和有效应力分别为σ和σE；两侧向为1、2方向.在加载过程中，由于泊松效应的影响，微结构中的某些薄弱部位（如骨料和砂浆交界面）会由于局部拉应变超过其极限拉应变而导致微裂缝的产生，走向大致平行于压力方向.

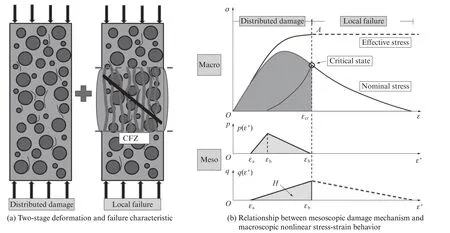
图2 单轴压缩示意图Fig.2 Shematic diagram of uniaxial compression

在分布损伤阶段（O→A），材料系统能够通过微裂纹随机萌生和扩展的方式，主动调节以实现微结构受力骨架的进一步优化，从而获得更大的承载能力，有效应力σE单调增大；A状态时，有效受力骨架调整至最优，σE达到最大值.名义应力σ呈现先增大后减小的趋势.该过程中微裂纹在整个试件范围内随机萌生和扩展，微裂纹密度维持在较小的程度，可近似地认为处于均匀变形状态.

A状态之后，材料系统已无法再通过微裂纹随机萌生、扩展的方式实现微结构受力骨架的进一步优化，潜在力学性能已发挥到极限，随即进入以局部灾变为特征的破坏阶段.在局部破坏区（CFZ）内，损伤进一步加剧，相继形成一系列的宏观纵向裂缝和剪切裂缝带；其余部位则出现卸载回弹现象.该阶段名义应力-应变曲线存在明显的尺寸效应，不能被看作纯粹的材料属性.定义A为临界状态，并将其作为损伤局部化和灾变破坏的前兆.

Van Geel［20］着重观测了混凝土损伤局部化现象，发现损伤局部化并不是出现在传统所认为的峰值名义应力状态，而是相对滞后，位于应力-应变曲线下降段的某个位置，局部破坏区以外的其余部位对软化段曲线也存在一定的贡献.这与本文模型中A状态（临界状态）位置的假设是一致的.

1.2.2 统计损伤本构模型

混凝土单轴压缩本质为三维空间的损伤演化过程，压缩方向损伤由泊松效应引起的侧向拉损伤过程控制［17］.引入变量ε+（ε+＞0），定义为压缩方向对应的等效传递拉损伤应变.对于单轴压缩，有ε+=-νε，ν为泊松比.本文中拉应力和应变为正，压应力和应变为负.

如图2（b）所示，压缩方向应力-应变行为由细观断裂、屈服2 种损伤演化过程控制，分别与微结构的“劣化”和“强化”效应对应.q（ε+）和p（ε+）分别为细观断裂、屈服损伤对应概率密度函数，假设服从三角形分布.图中横坐标应变量分别为ε和ε+.与ε+对应的特征应变包括εa、εh和εb，其中：εa为初始损伤应变；εh为p（ε+）峰值对应应变；εb为最大屈服损伤应变，同时为q（ε+）峰值对应应变.εcr为临界状态应变，满足εcr= -εb/ν.分布损伤阶段对应的本构关系可表示如下［17‑18］：

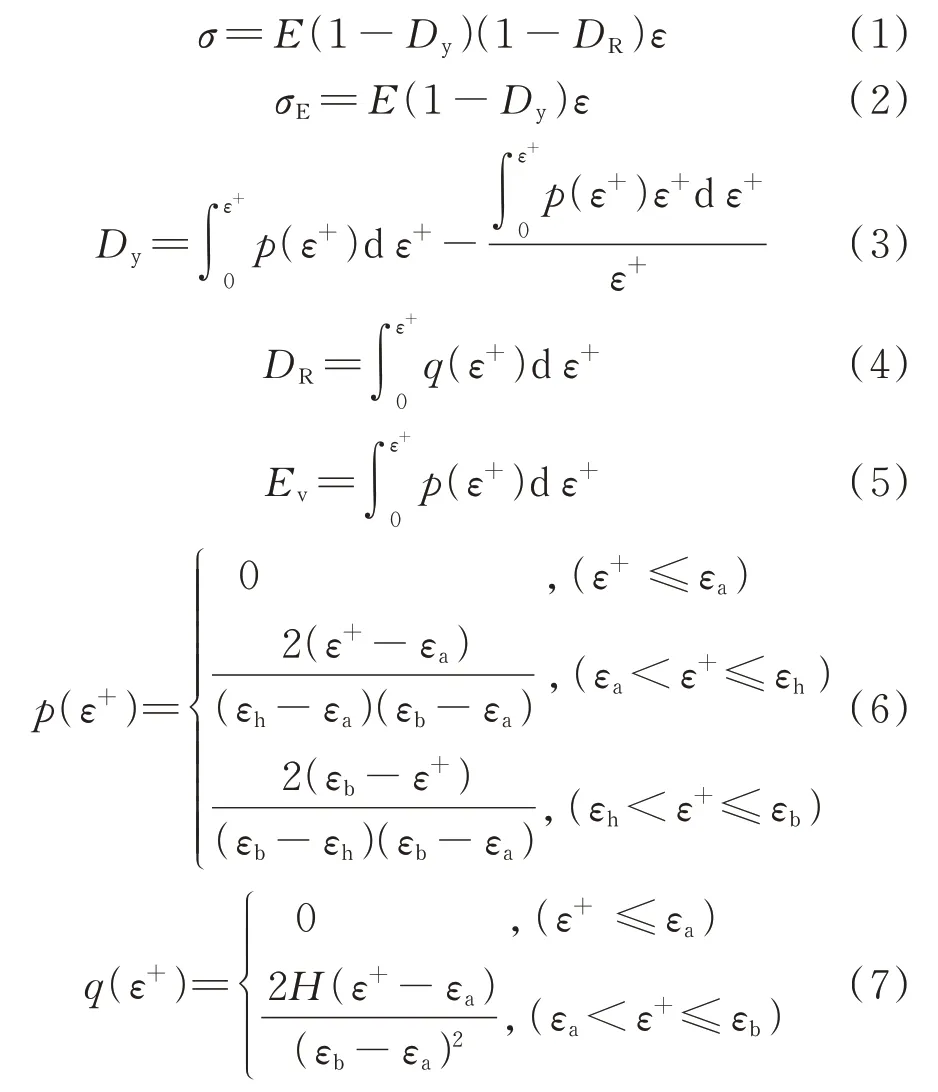
式中：DR和Dy为损伤变量，分别与细观断裂、屈服损伤相关；Ev为进化因子，表征微结构受力骨架优化调整的程度，变化范围0～1；H=DR（εb），为临界状态对应的断裂损伤值；εa、εh、εb和H表征细观屈服和断裂损伤演化过程对应的三角形概率分布形态，可用于分析混凝土细观非均质的损伤演化规律.

2 试验

2.1 材料

水泥选用河南丰博天瑞生产的P·O 42.5 普通硅酸盐水泥；砂为天然河砂（细度模数2.92，中砂）；天然粗骨料为连续级配天然碎石，再生粗骨料由校内翻修废弃混凝土路面经破碎、筛分后获得，粒径范围均为5～20 mm；拌和水为自来水.粗骨料的基本性能见表1.

表1 粗骨料的基本性能Table 1 Basic properties of coarse aggregates

2.2 配合比设计

取代率（R）为再生骨料占粗骨料总质量的百分比，分别考虑R为0%、50%和100%的3 种方案，试验配合比见表2.由于再生粗骨料吸水率较大，试验时添加附加水以保证粗骨料达到饱和面干状态.试件标准养护至28 d.

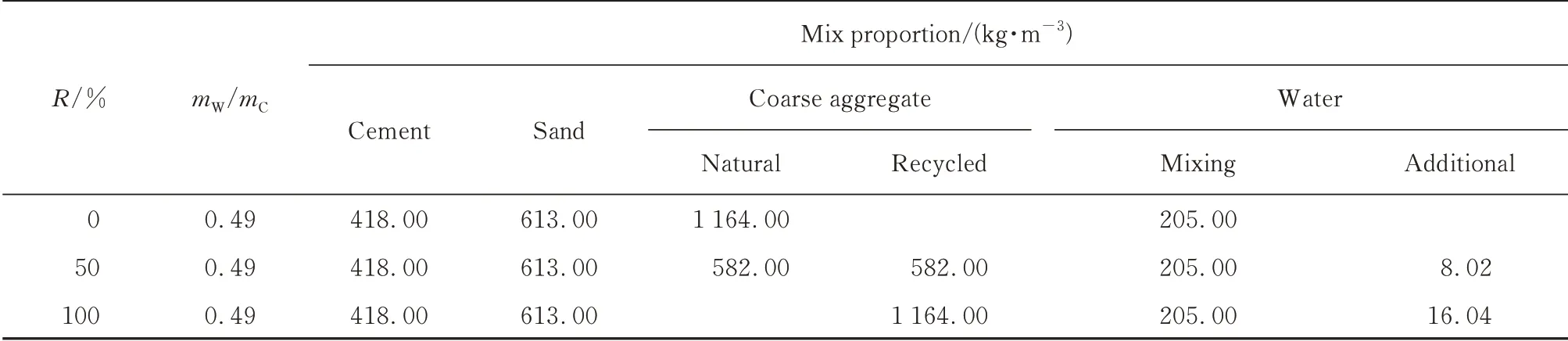
表2 配合比Table 2 Mix proportion

2.3 试验方法

试件尺寸为φ100×200 mm，总共制作12 组，每组5 个.在WAW‑1000 型电液伺服万能试验机上进行单轴压缩试验.加载过程采用位移控制的等应变率加载方式，应变速率ε̇采用10-5、10-4、10-3、10-2s-1，以ε̇=10-5s-1为基准应变速率.试件轴向力由试验机测试系统自动采集，试件两端纵向变形由位移计进行测量.试验数据处理过程中，考虑到试验结果的离散性，每组选取中间3 条试验曲线；通过以应变为基准，对3 条试验曲线数据点的应力值取平均的方法，获得平均应力-应变曲线作为该组的试验结果.

3 结果与分析

3.1 应力-应变全曲线

图3 为再生混凝土的单轴压缩名义应力-应变（σ‑ε）全曲线.由图3 可见：不同应变速率下再生混凝土的名义应力-应变曲线具有相似的形态特征，曲线上升段和下降段之间存在光滑的过渡；原点至60%峰值应力前的上升段基本为线性段，之后曲线斜率逐渐变缓，到达峰值后曲线迅速下降，应力下降到70%～80%峰值应力时下降段出现拐点，曲线由凸变凹，曲率变缓；随着应变速率的提高，峰值应力显著增大，曲线上升段和下降段连接部位变的更加陡峭.

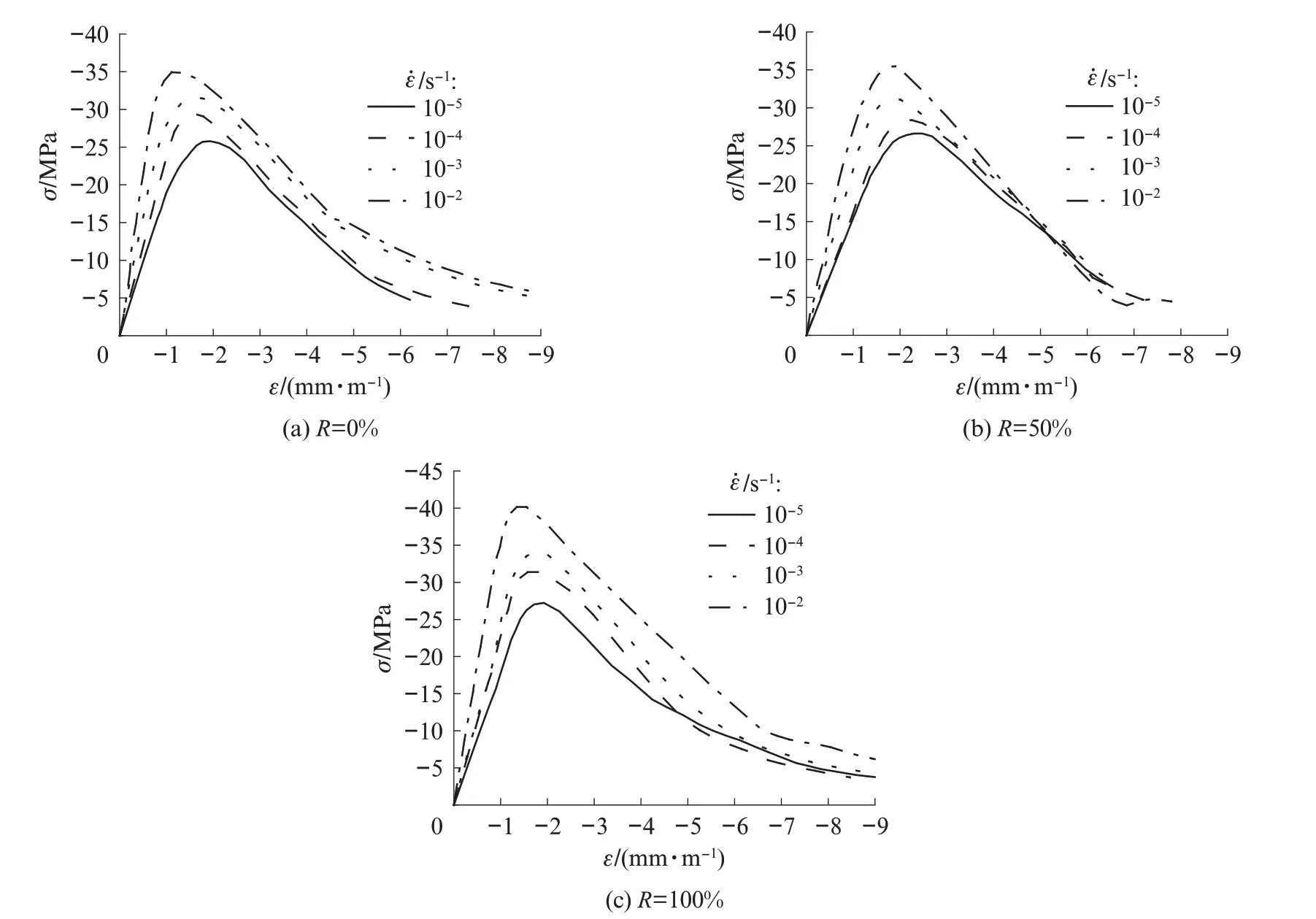
图3 再生混凝土的单轴压缩应力-应变全曲线Fig.3 Complete stress‑strain curves of recycled concretes under uniaxial compression

3.1.1 峰值应力

图4为混凝土峰值应力σp（抗压强度）随应变速率的变化.由图4 可见：在准静态工况下（ε̇s=10-5s-1），取代率R为0%、50%和100%的再生混凝土峰值应力分别为-25.79、-26.61、-27.24 MPa；在动态工况下，3 种混凝土的峰值应力均随应变速率的提高呈线性增长趋势；对于R=100%的再生混凝土，应变速率为10-4、10-3、10-2s-1时对应的峰值应力，分 别比准静态时提高15%、25%和47%；对于R=50%的再生混凝土，峰值应力分别提高了7%、17%和33%；对于R=0%的普通混凝土，峰值应力分别提高了14%、23%和35%.由此可见，当R=100%时再生混凝土动态强度的增大幅度要明显高于普通混凝土，这与文献［9‑10］的结论是一致的.

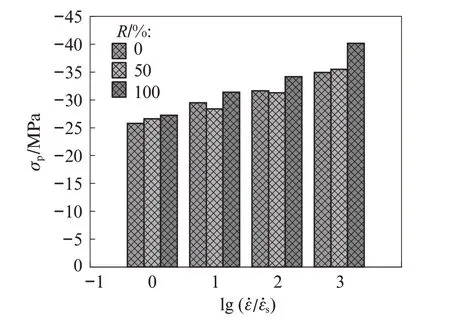
图4 混凝土峰值应力随应变速率的变化Fig.4 Change of peak stress of concrete under different strain rates

3.1.2 弹性模量

表3 为再生混凝土的特征参数，其中E为弹性模量，εp为峰值应变.由表3 可见：随着应变速率的增加，E近似呈线性增长；对于取代率R为0%、50% 和100%的再生混凝土，E分别由应变速率为10-5s-1时的19.7、15.7、17.9 GPa，增大到应变速率为10-2s-1时的41.1、26.8、40.4 GPa.王国盛等［4］和路德春等［5］结合Stefan 效应和惯性效应，对动态应变率下混凝土初始弹性模量增大的细观机理进行了探讨.

3.1.3 峰值应变

由表3 可见：对于取代率R为0%、50%和100%的再生混凝土，εp分别由应变速率为10-5s-1时的-1.93×10-3、-2.47×10-3和-1.92×10-3，减小到应变速率为10-2s-1时的-1.11×10-3、-1.94×10-3和-1.35×10-3；随着lg(ε̇/ε̇s)的增大，εp均呈减小趋势，显示混凝土脆性增大，延性降低.肖诗云等［21］和Dilger等［22］也得出了类似的结论.

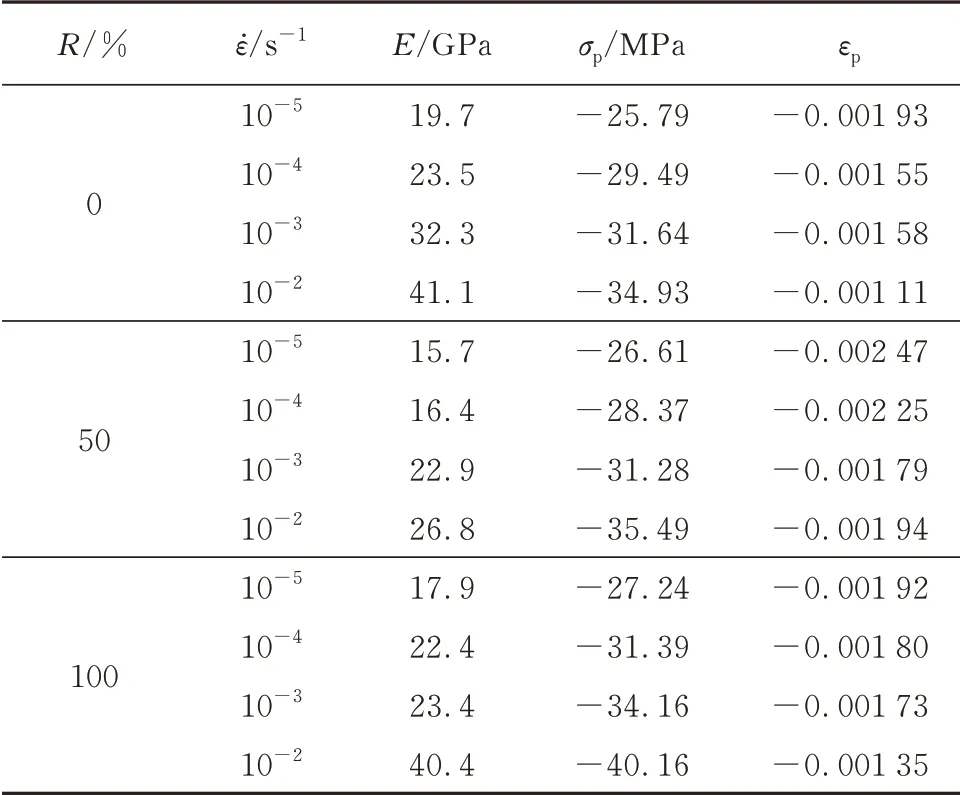
表3 再生混凝土的特征参数Table 3 Characteristic parameters of recycled concretes

3.2 变形破坏特征

再生骨料取代率对再生混凝土的变形破坏特征没有明显的影响.试件表面第1 条可见裂缝一般出现在峰值应力点附近，大致平行于受压方向.当达到应力-应变曲线下降段拐点附近时，在试件中间部位出现局部鼓胀现象，形成一系列纵向裂缝.随着损伤的进一步加剧，在局部鼓胀区内出现贯穿斜裂缝，导致试件最终的破坏.在低应变速率情况下，局部鼓胀与斜裂缝出现的间隔较大，局部鼓胀比较充分；在高应变速率情况下，局部鼓胀和斜裂缝出现的时间非常接近，部分试块没有出现明显局部鼓胀现象就直接出现斜裂缝.从裂缝形式来看，随着应变速率的提高，混凝土破坏裂缝越来越接近直线.从断裂面的形态可以发现，当应变速率较低时断裂表面粗糙，主要沿着骨料和砂浆交界面切断；随着应变速率的增大，断面更加平整，更多骨料被切断.试件破坏时会出现爆裂声，并伴随有碎块向四周飞溅.

白以龙等［15］基于突变理论，将准脆性固体材料破坏分为分布式损伤累积和诱发局部灾变2 个阶段，其中临界状态具有敏感性特征.结合本文试验，以出现局部鼓胀的状态作为损伤局部化的临界状态，将单轴压缩过程分为分布损伤和局部破坏2 个阶段.

3.3 细观损伤机制探讨

王国盛等［4］和路德春等［5］将有关混凝土动力特性细观机理的理论进行了总结，主要包括3 种观点：（1）黏性效应.主要来源于混凝土中的水泥基体.由于基体内部微孔隙中自由水的存在，孔隙在变形过程中会产生Stefan 效应，即产生阻止微孔隙扩展的阻力.（2）惯性效应.又称为应力波传播效应，是混凝土内部存在的一种能量传递过程.（3）裂纹扩展.动态荷载改变了基体内部裂纹萌生、扩展的形态、数量和路径，使混凝土强度得到提高.体现在2 个方面：一是对于单条裂缝而言，随着加载速率的提高，裂缝扩展的路径变得越来越平直，穿越骨料也越来越多；二是对于微裂缝系统而言，随着加载速率的提高，相同应力作用下混凝土试件中的裂缝数量减少.

上述因素对混凝土力学性能的影响可概括为2个方面：（1）导致初始“刚度”增大，可由弹性模量的变化进行表征.（2）改变了微裂纹萌生和扩展的路径、模式和累积演化过程，可用统计损伤模型进行定量表征.宏观非线性应力-应变曲线中蕴含着细观损伤演化过程的有效信息.本文利用统计损伤模型，结合试验曲线分析应变速率对再生混凝土单轴压缩过程中细观损伤机制的影响规律.参考文献［23］，泊松比ν取0.2.

图5 为利用损伤模型计算获得的再生混凝土在不同应变速率下分布损伤阶段对应的名义应力-应变曲线，包括上升段和部分下降段.每条预测曲线需要确定4 个参数：εa、εh、εb和H，可利用Matlab 遗传算法模块通过多元回归分析得到［18］.预测曲线与试验曲线吻合良好，计算参数见表4.

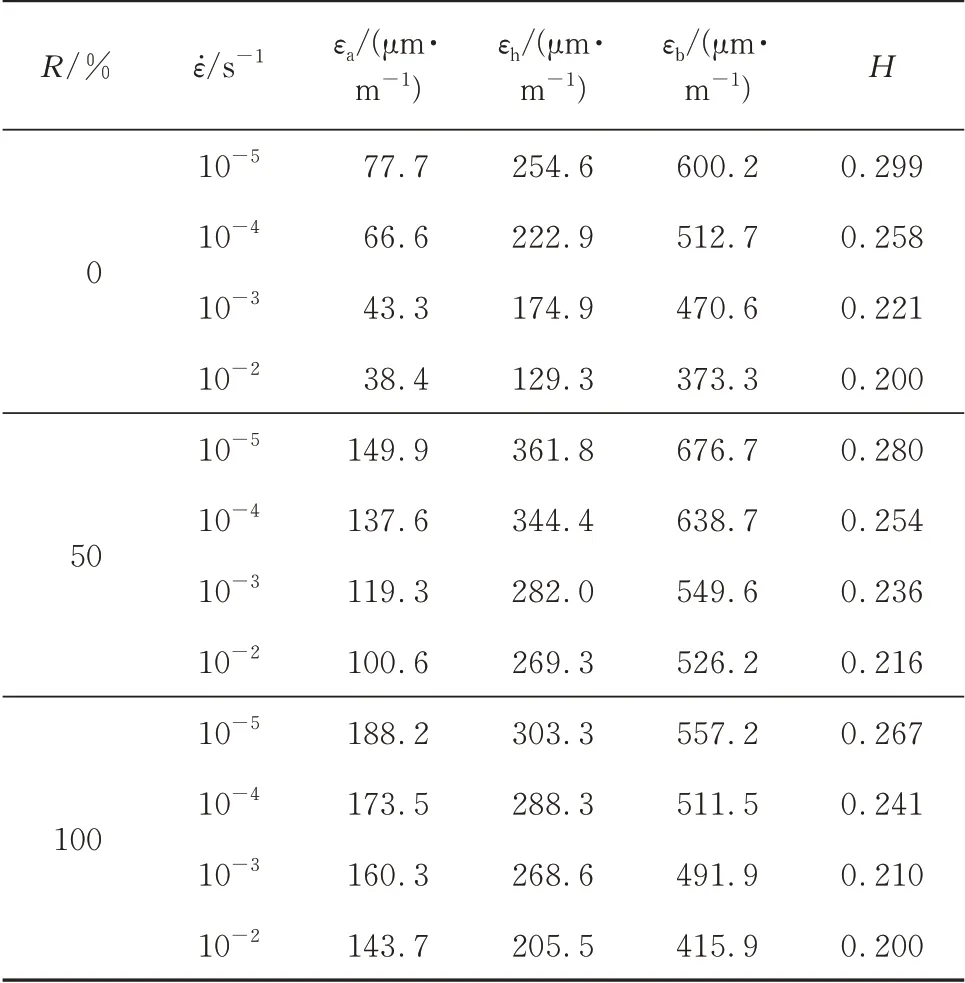
表4 再生混凝土的计算参数Table 4 Results for calculation parameters of recycled concretes

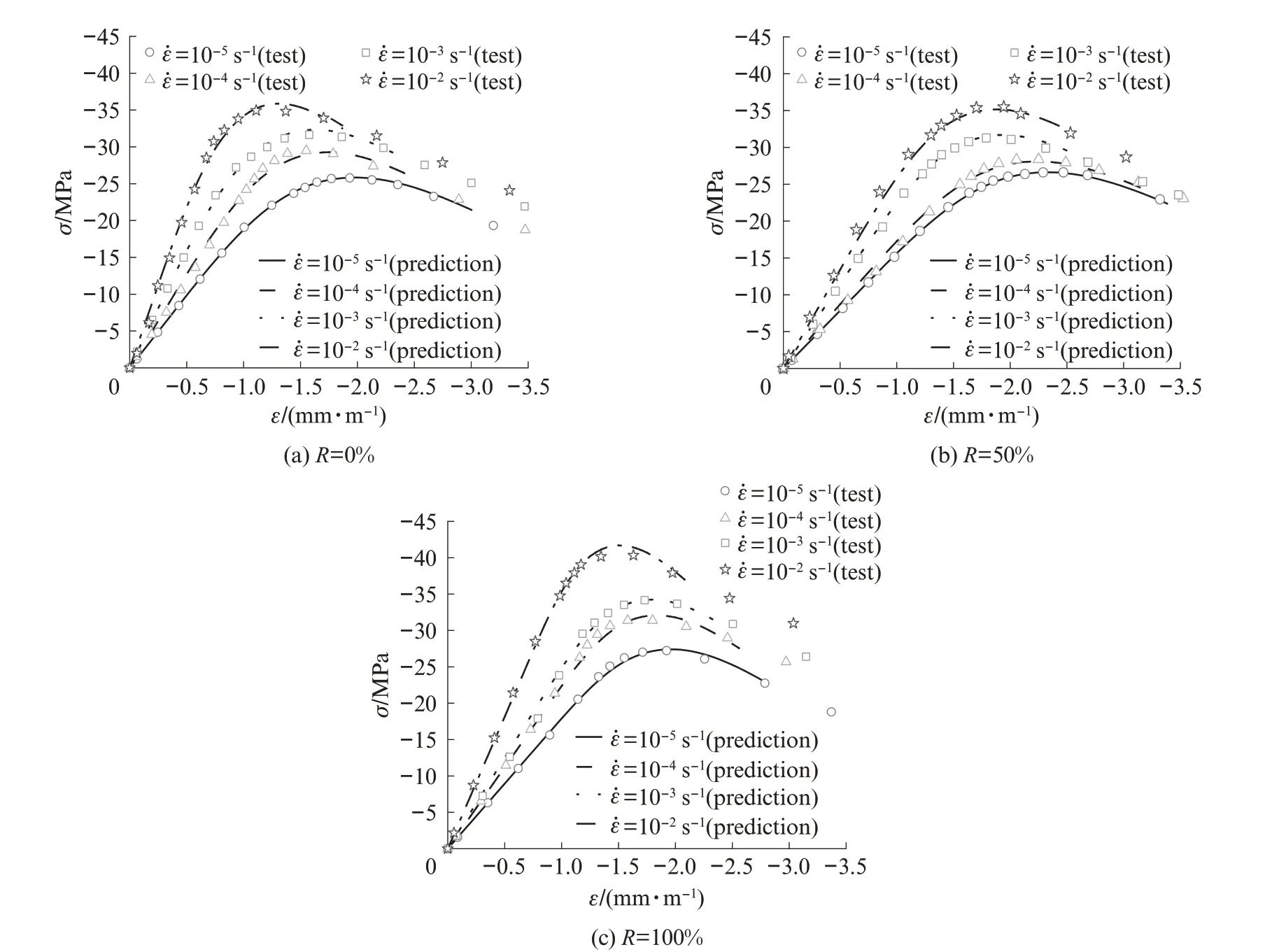
图5 再生混凝土的名义应力-应变曲线Fig.5 Nominal stress‑strain curves of recycled concretes

图6 为预测的再生混凝土有效应力-应变曲线，该模型从有效应力的角度理解整个变形破坏过程.由图6 可见：在分布损伤阶段，σ先增大后减小，中间存在峰值名义应力状态；σE单调增大，在临界状态达到最大值，随后试件将进入以损伤局部化为特征的破坏阶段；随着应变速率的增大，混凝土强度提高，延性降低，临界状态应变相应减小.

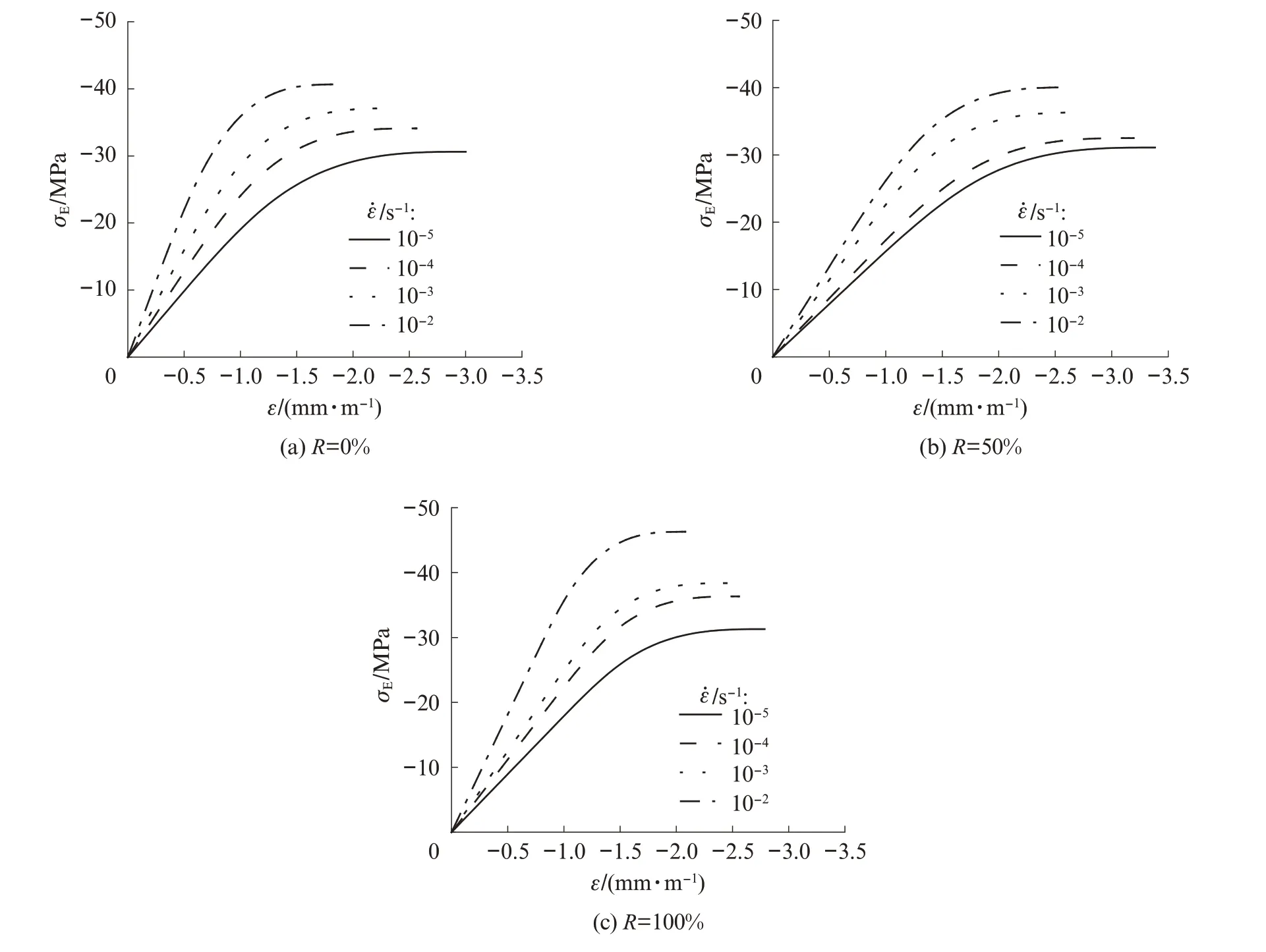
图6 再生混凝土的有效应力-应变曲线Fig.6 Effective stress‑strain curves of recycled concretes

图7 为再 生混凝 土的lg（ε̇/ε̇s）‑ε+关系 曲线，屈服损伤反映了混凝土微结构受力骨架优化调整的过程.由图7 可见：随着应变速率的提高，3 个特征参数呈现明显规律性的变化；由于延性降低，3 个参数均呈线性减小的趋势；对于R=100%的再生混 凝 土，εa和εb分 别 由 应 变 速 率 为10-5s-1时的1.882×10-4、5.572×10-4，减 小 到10-2s-1时 的1.437×10-4、4.159×10-4；对于R=0%的普通混凝土，εa和εb分 别由10-5s-1时的0.777×10-4、6.002×10-4， 减 小 到 10-2s-1时 的 0.384×10-4、3.733×10-4.

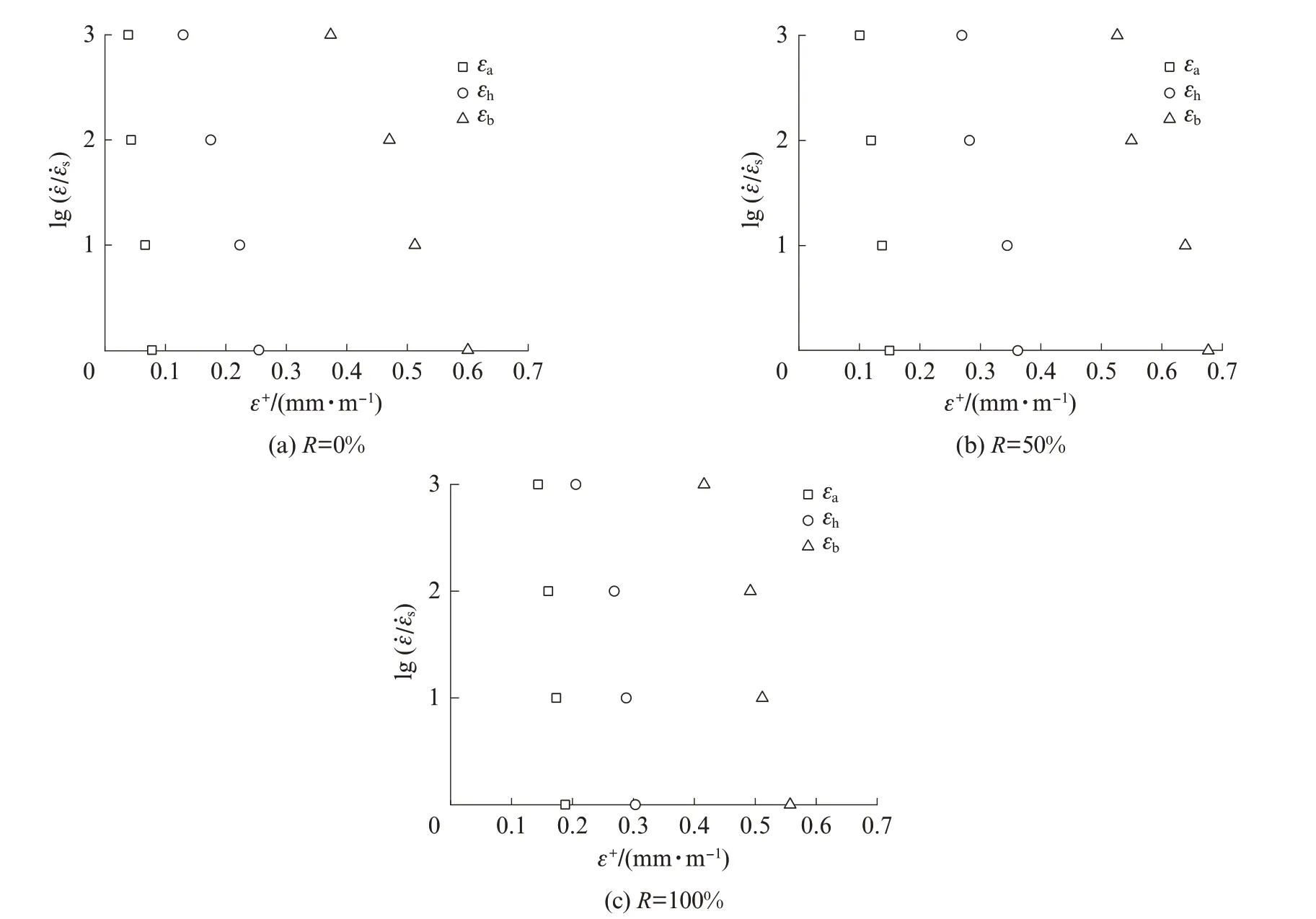
图7 再生混凝土的lg(ε̇/ε̇s)‑ε+关系曲线Fig.7 Curves of lg(ε̇/ε̇s)‑ε+of recycled concretes

图8 为 再 生 混 凝 土 的H‑lg（ε̇/ε̇s）关 系 曲 线.由图8 可见：随着应变速率的增大，H线性减小；对于R=100%的再生混凝土，H由应变速率为10-5s-1时的0.267，减小到10-2s-1时的0.200；对于R=0%的普通混凝土，H由10-5s-1时的0.299，减小到10-2s-1时的0.200.

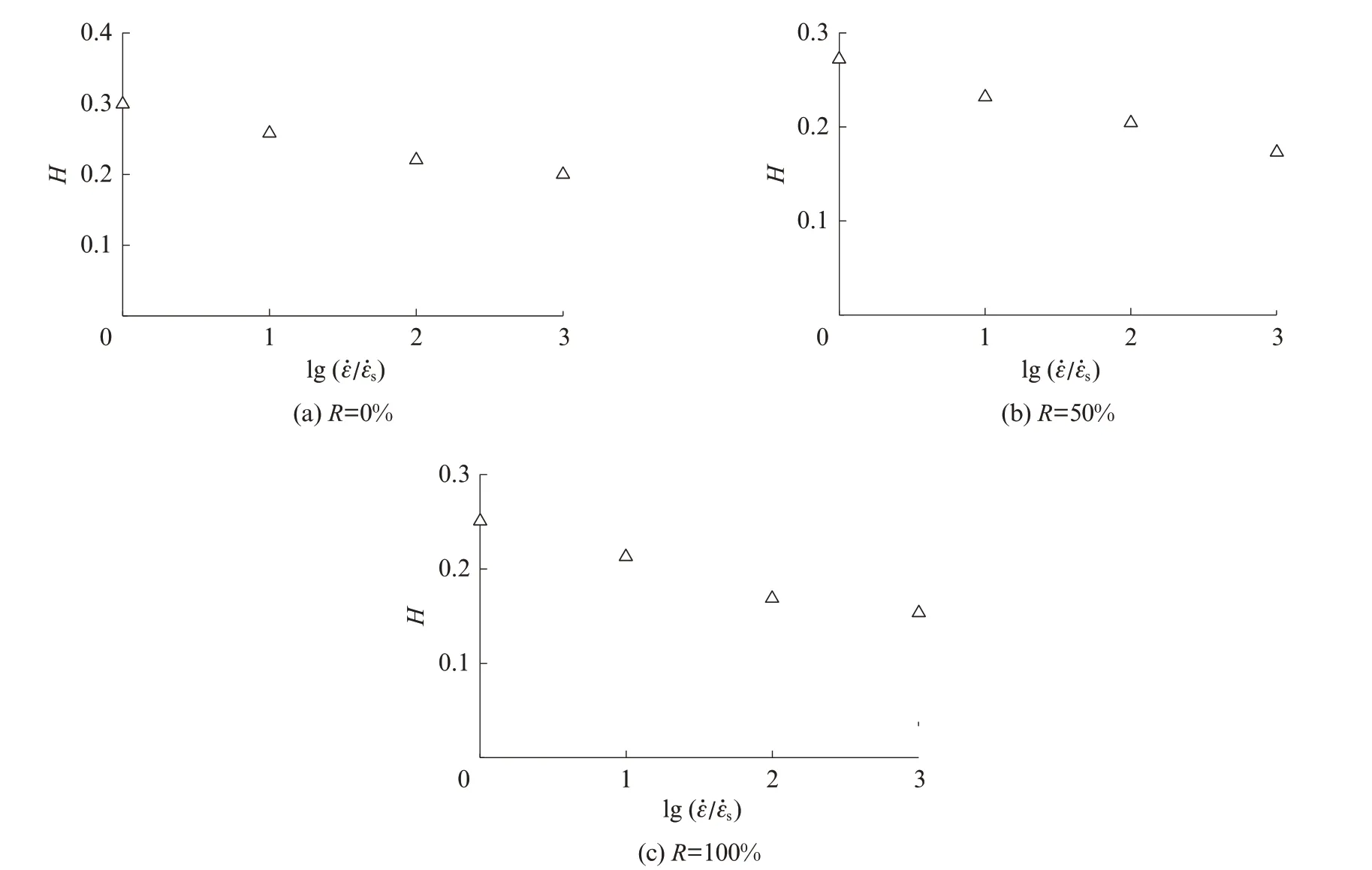
图8 再生混凝土的H‑lg(ε̇/ε̇s)关系曲线Fig.8 Curves of H‑lg(ε̇/ε̇s)of recycled concretes

图9 为再生混凝土DR的演化曲线.由图9 可见：在相同应变情况下，加载应变速率越高，DR值越大，即微裂纹密度越大；由于在高应变速率下混凝土更早地达到临界状态，导致临界状态对应的DR值随着应变速率的提高而减小；临界状态对应的微裂纹密度仍然维持在较小的范围.

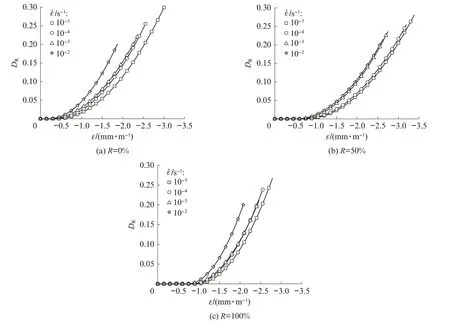
图9 再生混凝土DR的演化曲线Fig.9 Evolution curves of DR of recycled concretes

图10 为再生混凝土Ev的演化曲线.Ev与屈服损伤有关，在分布损伤阶段，Ev从0 增大到1，是材料损伤演化过程的决定性因素.由图10 可见，应变速率的提高显著改变了Ev的演化进程.从变形的角度看，在相同应变情况下，加载速率越高，Ev值越大.因此，在高应变速率下混凝土更早地达到临界状态，导致其变形能力降低，延性变差.当Ev=1 时，意味着微结构有效受力骨架调整到最优，材料潜在力学性能发挥到极限，有效应力达到最大值，试件随即进入以损伤局部化为特征的破坏阶段.整个损伤演化过程体现了量变到质变的转换.综合比较图6、7、10 可以发现，相较于普通混凝土（R=0%），再生混凝土（R=100%）的初始损伤应变明显偏大，同时动态工况下临界状态延性降低的幅度相对较小（ε̇=10-2s-1时，再生混凝土和普通混凝土对应的εcr分别为ε̇=10-5s-1时对应值的0.75和0.62），使得再生混凝土在动态荷载下有相对更充分的变形，最终导致再生混凝土在临界状态和峰值应力状态下的应力表现出更明显的率敏感性特征.

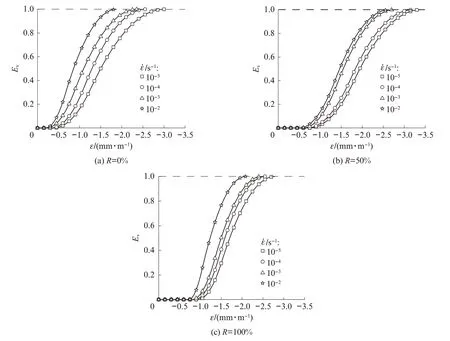
图10 再生混凝土Ev的演化曲线Fig.10 Evolution curves of Ev of recycled concretes

图11 为σcr/σp‑ε̇关系.由图11 可以看出，动态应变率下名义应力-应变曲线上临界状态与峰值应力状态对应的应力比值σcr/σp在0.74～0.93 之间，平均值为0.84.图12 为εcr/εp‑ε̇关系.由图12 可以看出，临界状态与峰值应力状态对应应变比值εcr/εp在1.37～1.62 之间，平均值为1.50.为了充分考虑混凝土材料的延性，同时避免考虑局部破坏阶段尺寸效应的影响，Xiao 等［24］提出将应力-应变曲线下降段对应85%峰值应力的状态定义为混凝土单轴压缩过程的极限状态.可见本文模型中临界状态位置与文献中极限状态位置是一致的.

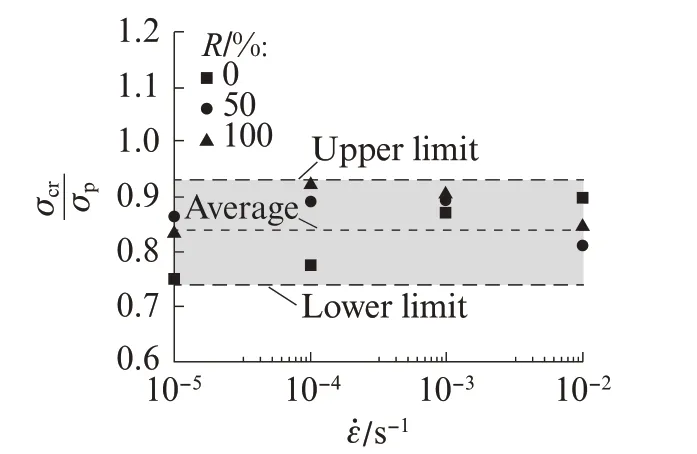
图11 ̇关系Fig.11 Relation of

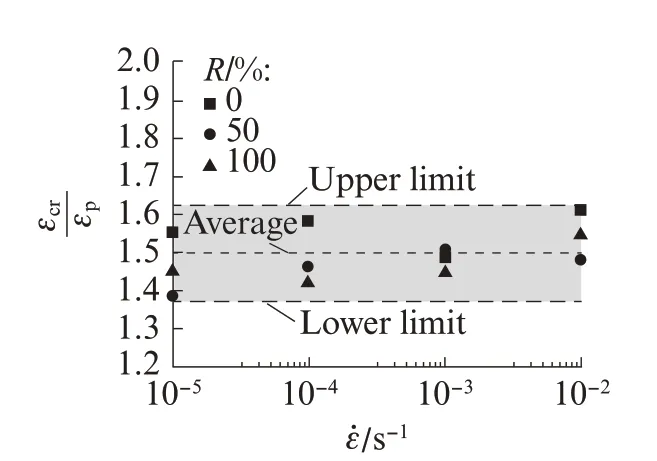
图12 ̇关系Fig.12 Relation of

4 结论

（1）再生混凝土在动态加载条件下表现出与普通混凝土类似的力学特性和变形破坏特征.随着应变速率的提高，峰值应力和弹模量线性增大，峰值应变逐渐减小，曲线上升段和下降段的连接部位变得更加陡峭.当R=100%时，再生混凝土表现出更为显著的动态敏感性特征，应变速率为10-2s-1时的峰值应力较准静态时提高了47%.再生混凝土的动态力学特性与内部裂纹扩展过程存在着密切的联系，随着应变速率的增大，断裂面更加平整，更多的骨料被切断.

（2）加载应变速率的提高显著改变了微结构受力骨架优化调整的进程，使得混凝土更早地达到临界状态，导致其变形能力降低，延性变差.与此同时，应变速率的提高改变了微裂纹萌生、扩展的路径和过程，临界状态时断裂损伤值线性减小.与普通混凝土相比，动态工况下再生混凝土在均匀损伤阶段具有相对更好的延性和变形能力，从而表现出更加显著的应变率敏感性.区分峰值应力状态和临界状态，σcr/σp和εcr/εp的均值分别为0.84 和1.50，建议将临界状态作为本构模型的极限破坏状态.