基于高增益扰动观测器的反演控制方法研究

樊建升，刘泽军

(1.山西焦煤能源集团股份有限公司，山西 太原 030006；2.古交西山发电有限责任公司, 山西 太原 030024)

一直以来，反演控制因其稳定、结构化、非线性设计的优点，被广泛研究并应用[1].反演控制方法的提出与应用，主要解决了一些系统自身满足严反馈结构的非线性系统的控制器设计问题。同时，在部分非线性系统的结构化设计问题上，反演控制也具有相当的处理能力。根据反演控制的原理，在设计过程中，反演控制要求获得系统的精确数学模型。然而，实际非线性系统模型中，存在大量的系统假设，加上系统本身具有的参数时变及时滞特性、不确定性外界干扰、以及强耦合、变量之间的隐式非线性、指数或分数等复杂非线性关系等因素，系统模型往往存在偏差或部分未知。同时，非线性系统中存在的高阶高维状态变量、多输入输出、耦合等因素，传统的反演控制设计往往还会导致控制系统性能变差[2].

在一些复杂系统中，系统状态往往难以测量。状态观测器根据系统输入输出估计系统内部状态[3].常被研究与应用的观测器有：高增益观测器、扩张状态观测器、滑模观测器以及卡尔曼滤波器等[4-7].此外，扰动观测器作为一种在线估计算法，将系统不确定性、未建模动力学和外部扰动的组合效应聚合为扰动项，在模型不确定性的复杂系统状态获取和控制改进上显示出了优势[8].在扩展状态空间模型的基础上，扰动观测器主要应用于估计标称对象模型中未考虑的集中不确定性。一些研究如滑模扰动观测器、非线性扰动观测器以及作为扩展阶线性观测器的高增益扰动观测器等，将扰动观测器引入不同控制设计，解决了状态或非线性扰动的获取问题。由于高增益扰动观测器的稳定性易保证和简单设计等优点，常被用于实现功能估计和补偿[9].

为此，本文提出了一种基于高增益扰动观测器的反演控制设计方法。首先，扩张系统状态，引入虚拟项替代系统扰动；其次，基于高增益扰动观测器原理设计观测状态，获得用于替代真实系统非线性项的函数表达式；最后基于反演控制，设计虚拟控制器和实际控制器。将本文算法应用于一个三变量的非线性系统，通过仿真验证方法的可行性和有效性。

1 简单化工模型

三变量非线性釜系统在零动态稳定下的状态空间方程如下[10]：

(1)

其中，各参数值分别为Da1=3.0、Da2=0.5和Da3=1.0.

由式(1)可以看出，此过程具有状态耦合和非线性等特点。常规控制方法需要经过解耦和模型转换实现控制设计。当存在不确定性和较大的未知噪声干扰时，控制设计变得无效。

2 基于高增益扰动观测器的反演控制方法

为便于后续控制设计，对系统状态变量进行顺序定义以满足反演控制框架要求，令x1=x3,x2=x1,x3=x2.

2.1 高增益扰动观测器

高增益扰动观测器用于式(1)的状态空间，定义一个虚拟状态来表示系统扰动，即ψ4(·)，将原3阶系统扩展为4阶系统。因此，系统的四阶HGPO设计如下：

(2)

其中，[α1/ε,α2/ε2,…,αn-1/εn-1,αn/εn]T为观测器增益，且0<ε<1.并且，观测器增益是根据扰动导数的上界确定的。需要指出的是，对于HGSPO的设计，只需要测量输出和输入。

2.2 控制设计

反演控制设计的基本思路是：1)将系统设计为多个不超过系统阶数的级联子系统，以进行递阶控制设计。2)子系统逐级设计Lyapunov函数，在子系统收敛的条件下，推导虚拟控制器，并将子系统的虚拟控制器作为下一级子系统的跟踪目标。经过逐级推导，最终得到实际控制器。反演控制基于Lyapunov函数的设计保证了闭环系统的一致收敛。

在进行控制设计之前，首先通过高增益状态扰动观测器对系统进行观测，以在观测状态中包含系统未建模以及干扰等非线性因素，其次通过低通滤波对直接配置得到的未知非线性估计项滤波，避免干扰数据引入控制设计中。最后，基于反演控制设计控制器。控制框图见图1.

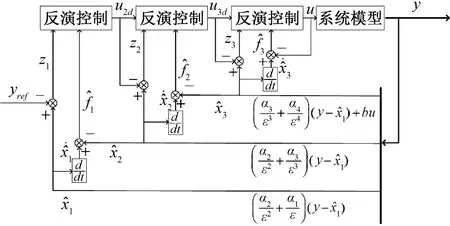
图1 基于高增益扰动观测器的反演控制框图

首先，求取状态一阶导，获得新的状态空间为：

(3)

(4)

因此，设计虚拟控制器和实际控制器如下：

(5)

通过低通滤波器对虚拟控制器求导，并将式(5)代入式(4)中，可以得到Lyapunov总函数可以写为如下形式：

(6)

在观测器收敛情况下，通过选择适当控制参数ci，可以保证闭环系统最终一致有界。

3 仿真结果分析

通过实际系统仿真，在matlab2016b环境下对本文方法进行验证。参数分别选取为：系统初始状态以及观测器的初始状态均设置为[0.15 0.2 -0.1]T.系统采样时间设置为Ts=0.001 s，总时长为ts=30 s.引入零均值高斯白噪声noise=0.01×randn(size(0.01,1),N),N=ts/Ts.观测器参数选取为α=[110,2 000,800,1 000]T,b=1 000,ε=0.05.选取可行的控制器参数c=[5,9 000 000,92 900]T,η=1011.选取低通滤波器带宽为τ=0.1,dt=0.001.得到图2和图3所示的结果。

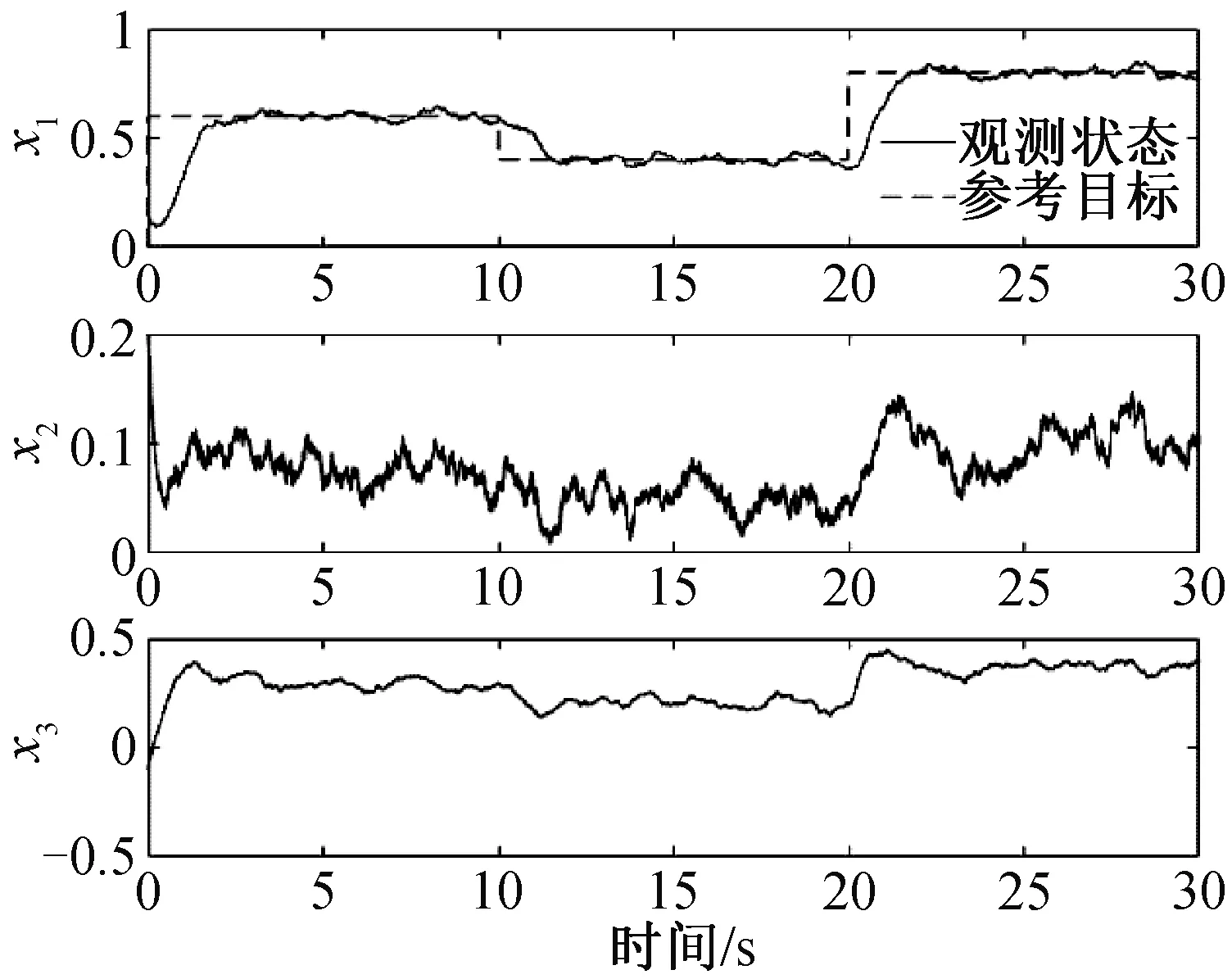
图2 高增益扰动观测器下闭环系统的状态追踪效果图

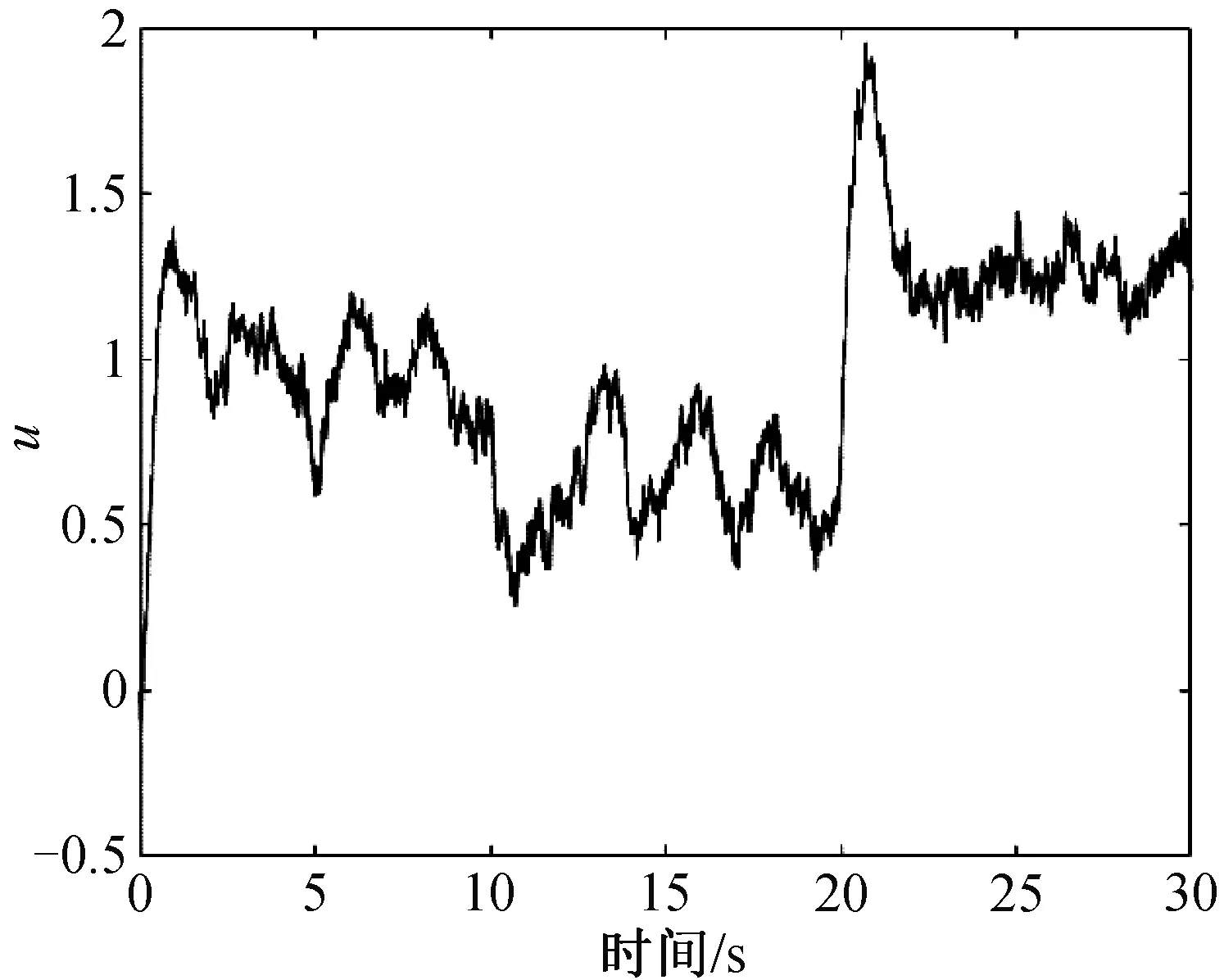
图3 高增益扰动观测器下闭环系统的控制输入图

通过上述仿真，结果显示出在该控制设计下，基于高增益扰动观测器的反演控制设计可行，系统稳定运行，追踪效果收敛，获得较好的鲁棒性。但高增益扰动观测器具有放大噪声的功效，尽管通过高增益扰动观测器，实现了系统模型不确定下的控制，但观测状态中的噪声仍然较大。计划在后续工作中改进观测器设计，以实现噪声干扰的抑制。

4 结 论

本文提出了一种基于高增益扰动观测器的反演控制方法。在传统反演控制设计基础上，引入高增益扰动观测器，实现在仅知系统输入输出和阶数的状态观测，并包含了模型不确定性因素。在状态已知基础上，系统非线性项的配置与估计用于反演控制设计中，保证了闭环系统在不确定或已有非线性因素下，具有良好的稳定性和性能表现。通过三变量的化工过程仿真，结果验证了该方法的有效性。