基于客流直达的城市轨道交通跨站停开行方案优化研究

杨安安 ，汪 波，陈绍宽，张翕然

（1. 北京市智慧交通发展中心，北京 100161；2. 综合交通运行监测与服务北京市重点实验室，北京 100161；3. 北京市地铁运营有限公司，北京 100044；4. 北京交通大学，北京 100044）

近些年，随着中国城市轨道交通网络的不断发展，客流特征也发生了较大变化。客流强度大、出行距离长、时空分布不均衡等问题日益突出。与此同时，公众对出行服务质量的要求也逐渐提高，这些对轨道交通运营组织都提出了更高的要求。

以北京轨道交通为例，截至2019年底，北京轨道交通日均进站量突破600万人次，人均出行距离超16 km。在传统站站停运营模式下，出行距离长意味着停站数量增多。以平均站间距2 km计算，北京轨道交通人均停站次数约8个站。累计停站次数分布规律显示：约60%的出行停靠次数在 8站以上，40%的出行停靠次数在12站以上。Vuchic[1]指出对于10～20 km的中长距离出行而言，站站停运营方式下的列车平均运行速度明显偏低。相关数据显示，现行站站停运营模式下北京轨道交通平均运行速度仅为 35 km/h，远低于80 km的设计时速。因此，结合出行需求，减少列车停靠站数、提高列车运行速度是轨道交通运营组织的一个重要的研究方向。

目前，世界各地采用的非站站停方式主要有2种[1]，即快慢车(local-express)模式和 A/B跨站停(A/B skip-stop)模式。快慢车运营指线路中有快车和慢车两种类型列车，车站有2类，E站和L站。快车只停靠E站，慢车则每站都停靠。A/B跨站停运营模式下有A车和B车两种类型的列车，车站有3类，A、B、AB。其中A车跳A站，B车跳B站，AB站为两类车都停靠的车站类型。两种运营模式下的列车运行图如图1所示。快慢车运行效率高，但线路往往需要配备越行设施，如纽约、芝加哥和费城都有3到4条轨道线能够同时独立运行快车和慢车。无越行条件的双轨线是我国城轨主要配线形式，这种情况下跨站停模式更合理，且已在智利圣地亚哥地铁成功应用。

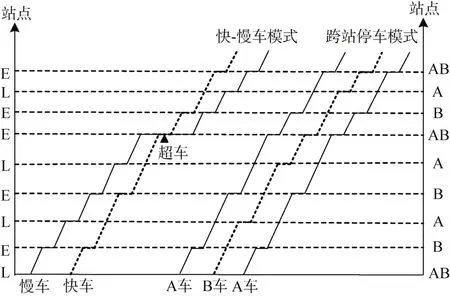
图1 快慢车和跨站停车模式下列车运行示意Figure 1 Train operation diagram for express-local and skip-stop operation modes

A/B跨站停运营模式具有提高列车运行速度、缩短乘客乘车时间、减少车辆数、均衡列车上座率的优势[2]。Vuchic[1,3-4]对A站、B站、AB站的分布以及跨站停的影响提出了很多建设性意见，如应尽可能减少A-B站连续组合，以减少乘客的反向绕行；郑锂等[5]建立了以乘客总出行时间最小的跨站停车方案优化模型；Freyss等[6]则采用连续逼近方法(具体可参阅文献[7])对最佳站点密度等进行求解；Yang等[8]考虑了线路条件以及乘客需求特征，构建了适用于实际场景的跨站停方案优化模型；曹志超等[9]提出带有0-1决策变量的双目标非线性混合整数规划模型，并采用理想点法和禁忌算法进行求解；王智鹏[10]引入了乘客候车惩罚系数，建立了动态停站时间跨站开行方案模型。

A/B跨站停模式的缺点在于部分乘客需要换乘才能到达目的地。如图2所示，对于从A站到B站的OD(如站点1到站点2，站点1到站点5)，在A/B跨站停模式下乘客需先乘B车在某AB站下车后，再换乘A车。若OD之间没有AB站，乘客还需要反向折回才能到达目的地车站。

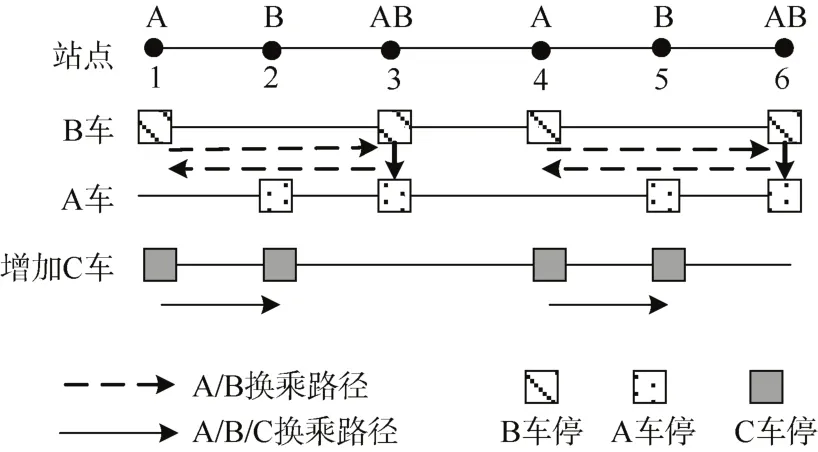
图2 两种停站模式下乘客换乘路径Figure 2 Passenger interchange paths in two stop modes

针对上述A站到B站出行OD必须要换乘这一问题，现提出增加第3种列车C(如图2)。且C车需满足同时停靠A站和B站，在AB站部分跳停。事实证明，只要保证每类车站至少有两类列车停靠即可实现所有站点间均有列车直达。

综上，本文的研究问题归纳为：基于双轨无越行条件的线路，已知线路的实际客流OD，以最小间隔、列车满载率、可用车辆数等为约束条件，构建 A/B/C跨站停开行方案优化模型。通过优化3类列车的停站方案和发车频次，最小化乘客出行时间。

1 A/B/C跨站停开行方案优化模型构建

如图3所示，将线路站点进行编号(1至m)，其中1、m分别表示始发站和终点站，该线路上开行A、B、C共3类不同停站方案的列车。

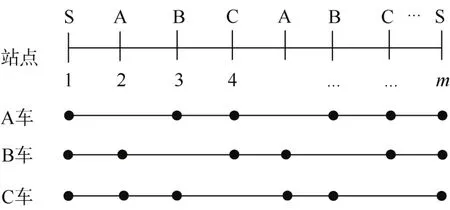
图3 A/B/C跨站停运营模式下列车停站方案示意Figure 3 Schematic diagram of the stopping schemes under A/B/C skip-stop operation mode

列车与站点的对应关系设置为：A车跳A站，B车跳B站，C车跳C站，S站表示3类列车全停站。且A车、B车和C车按照相同的发车间隔交替驶出始发站。

1.1 决策变量

1.2 符号

1) 常用下标和集合(见表1)。

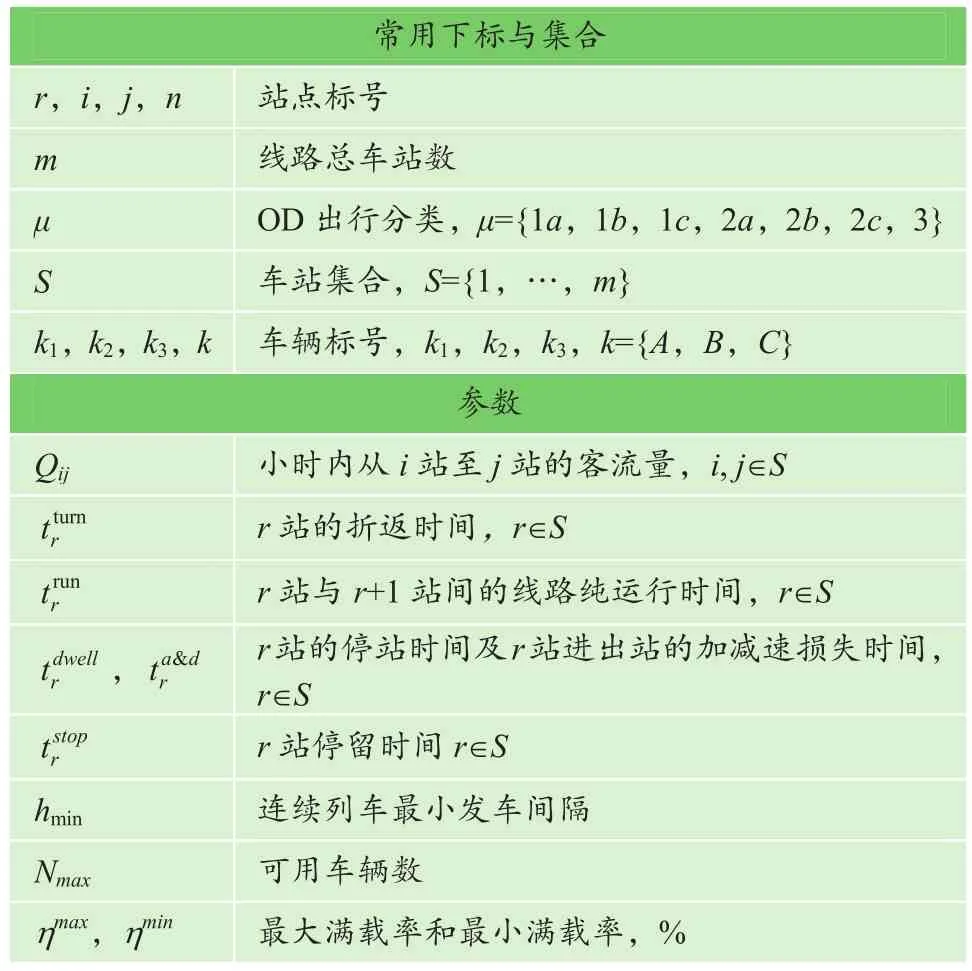
表1 符号解释Table 1 Symbol explanation

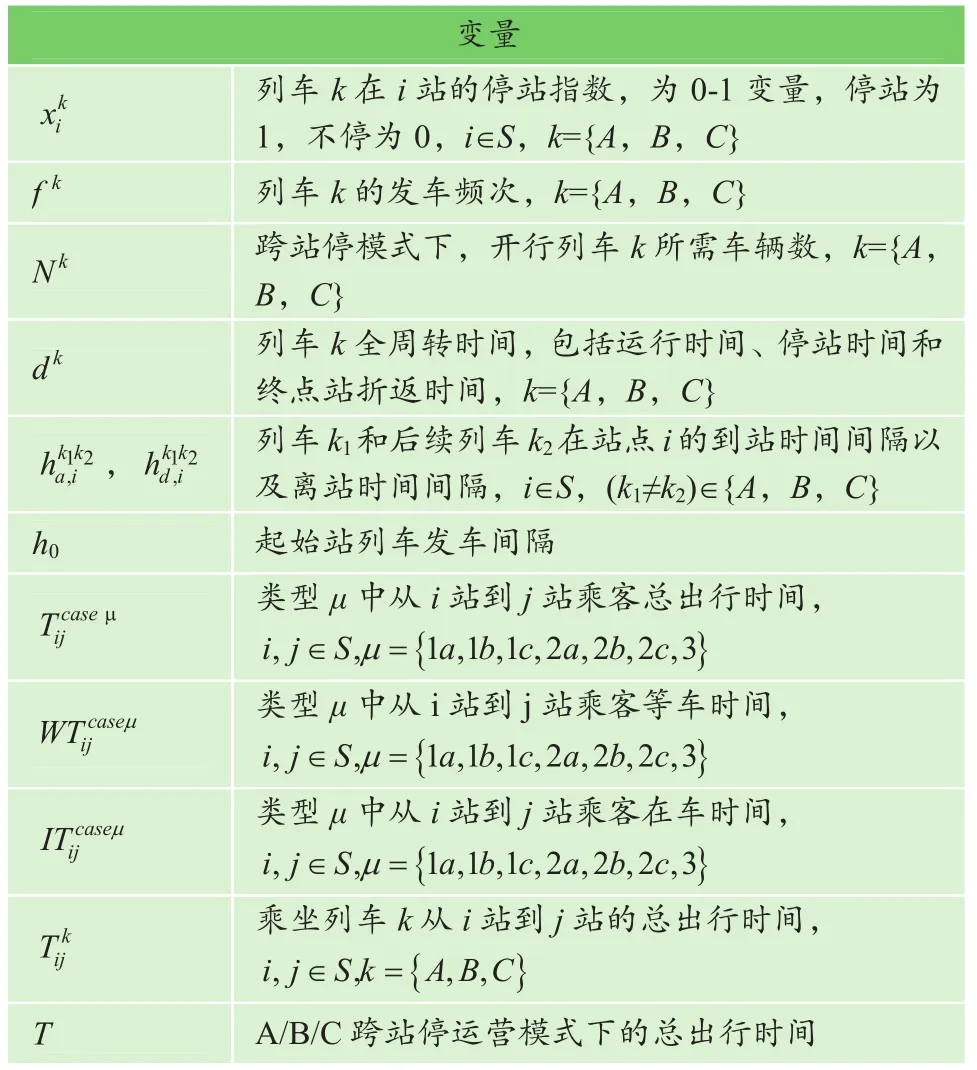
续表

1.3 假设

简化问题的需要，本文提出如下假设：

1) A/B/C 3类列车在起始站以相同间隔交替发车，车底独立、互不混用；

2) 乘客到达服从均匀分布；

3) 相邻站点之间的纯运行时间(不包括加减速时间)固定，与列车停站方案无关；

4) 上下行方向停站时间和区间运行时间一致；

5) 乘客将乘坐首列可直达目的地站点的列车，即不考虑列车拥挤引起的滞留和乘客换乘问题。

1.4 模型构建

1.4.1 基于可乘坐列车类型的OD分类

乘客出行起讫点(OD)车站属性不同，乘客可乘坐的列车种类也不同。因此，以下根据可乘坐的列车种类数量将乘客出行划分为1、2、3三类，分别表示可乘坐1种列车，2种列车，以及3种列车都可乘坐的OD。

1) 类型1。乘客出行起讫点只有1种列车可实现直达。如图4所示，根据具体可乘坐列车的类型，此类乘客可进一步分为以下3小类：

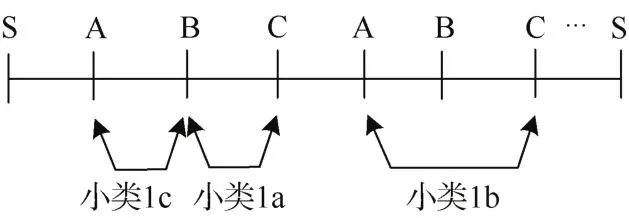
图4 类型1中OD站点类型划分Figure 4 Classification of OD for Type 1

①小类1a：出行起讫点为B站至C站(或C站至B站)，此类乘客可乘坐A车；

②小类1b：出行起讫点为A站至C站(或C站至A站)，此类乘客可乘坐B车；

③小类1c：出行起讫点为A站至B站(或B站至A站)，此类乘客可乘坐C车。

2) 类型2。乘客出行起讫点有2类列车可直达，如图5所示。

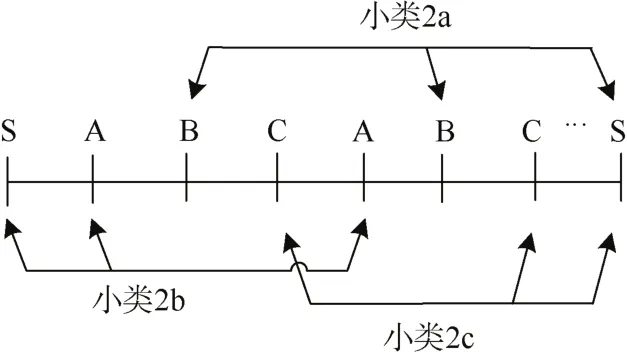
图5 类型2中OD站点类型划分Figure 5 Classification of OD sites for Type 2

①小类 2a：出行起讫点为B至C站(或B站至S站、S站至B站)，此类乘客可乘坐A车和C车；

②小类 2b：出行起讫点为A至A站(或A站至S站、S站至A站)，此类乘客可乘坐B车和C车；

③小类 2c：出行起讫点为C至C站(或C站至S站、S站至C站)，此类乘客可乘坐A车和B车。

3) 类型3。乘客出行起讫点3类车全停，出行起讫点为S站至S站，此类出行乘客3类列车都可直达，这也是 A、B、C跨站停模式下最受益的乘客类型，如图6所示。

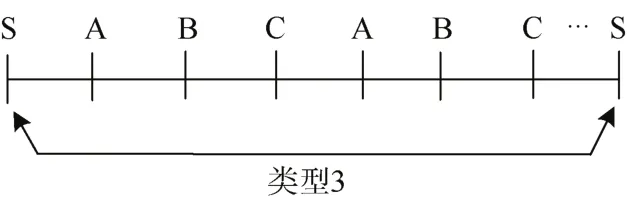
图6 类型3中OD站点类型划分Figure 6 Classification of OD for Type 3

1.4.2 各类型客流占比

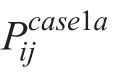
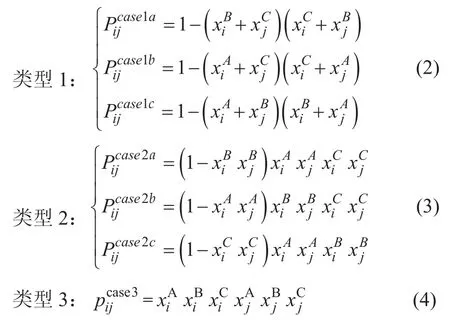
可以验证，以上3大类客流占比公式的总和为1，涵盖了所有客流类型。结合以下各类客流出行时间计算公式，即可计算出线路每个OD的总出行时间。

1.4.3 各类型乘客出行时间

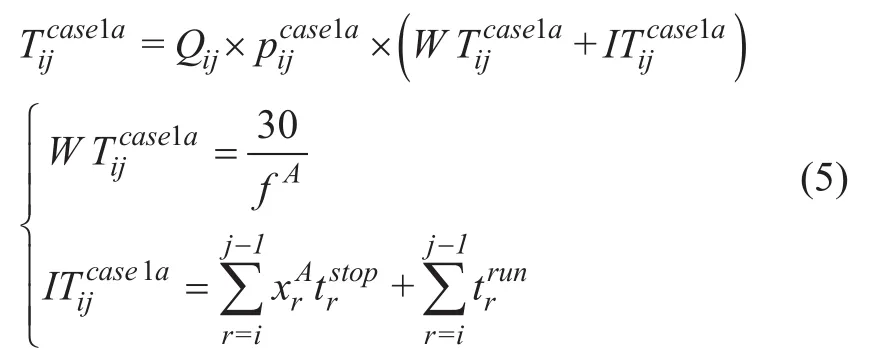
同理，小类1b和1c出行时间计算公式与1a相似，这里不再赘述。

2) 类型2。以小类2a为例，可乘坐列车A或者列车C。各部分时间如下：

故小类2a乘客的出行时间表达式为：

同理，小类2b和2c出行时间计算公式类似，这里不再赘述。

3) 类型3。3类列车都可实现直达，其出行时间表达式为：

综上，该线路所有客流总出行时间表达式为：

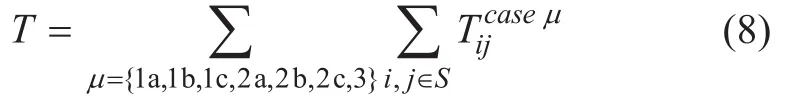
随着信息技术的发展，乘客可通过多种方式获取列车时刻表，提前规划出行时间。同时，车次多样化，也会促使乘客提前掌握出行信息，以便选择合适车次出行。简而言之，对于乘客而言，候车时间变得越来越可掌控。因此，有必要对不考虑候车时间，仅对乘客在车时间进行分析。根据以上各类出行时间的分析，乘客总在车时间表达式为：

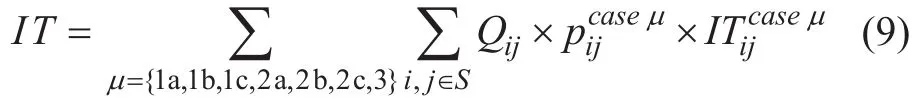
1.4.4 约束条件

1) 发车频率和停站方案约束关系。基于文中的假设1)，在起始站，A/B/C 3类列车以同等间隔交替发车，则起始站各类列车间距为此外，因同类型列车运行线相互平行，A/B/C 3类列车交替循环发车，故只要A列车和后行列车B，B列车和后行列车C，C列车和后行列车A在每个站满足最小安全间隔要求，即可实现线路所有列车之间满足最小安全间隔要求。

如图7所示，以列车A和后续列车B的发车间隔为例，公式(10)(11)表示同一站点发车间隔与到达间隔，以及停站指数的关系。

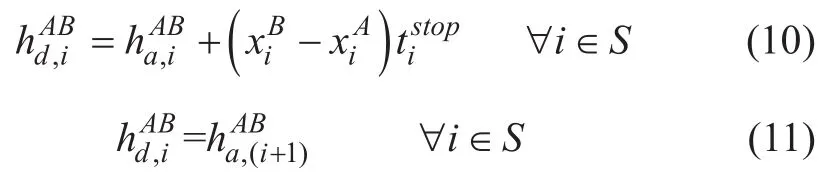
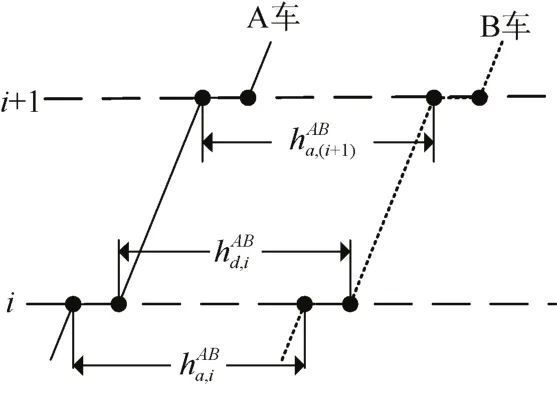
图7 发车间隔示意Figure 7 Schematic diagram of departure intervals

因此，我们可从起始站发车间隔h0推导出任意站点发车间隔公式公式，如式(12)：

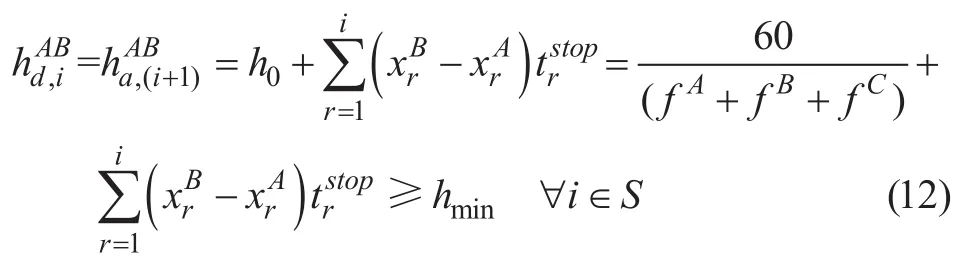
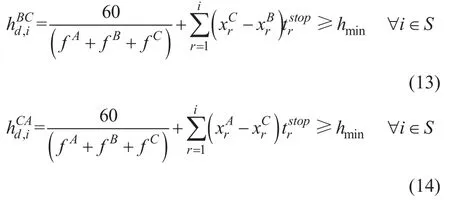
2) 最大满载率约束。用ur表示站点r至站点r+1，(或r+1至r)的最大断面客流，发车频率需满足以下约束：

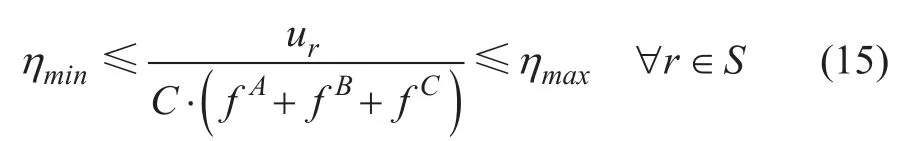
3) 可用车底数约束。基于假设1)中3类列车交路车底独立，约束如下：

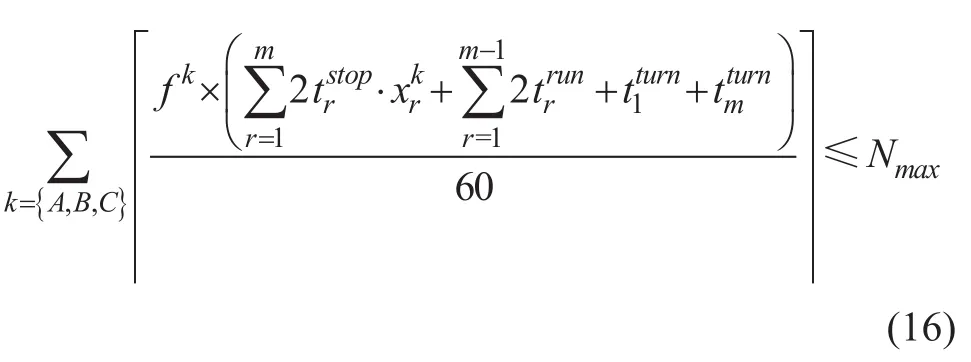
4) 其他约束。

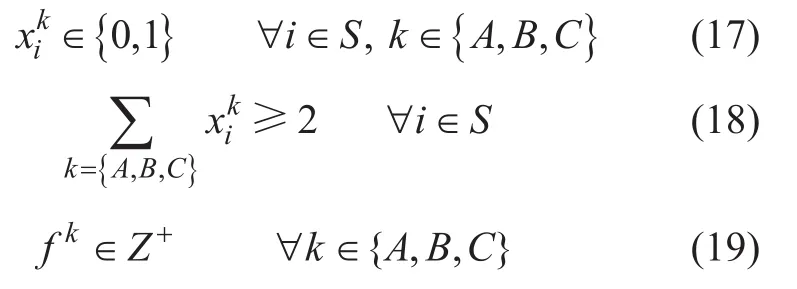
公式(17)表示停站指数为0-1变量，公式(18)表示任意一个站至少有 2趟车停靠约束，公式(19)表示发车频率为整数。

2 算法设计

本文采用遗传算法求解城市轨道交通A/B/C跨站停运营方式下的开行方案编制问题，通过Matlab软件编程实现，算法流程如图8所示。

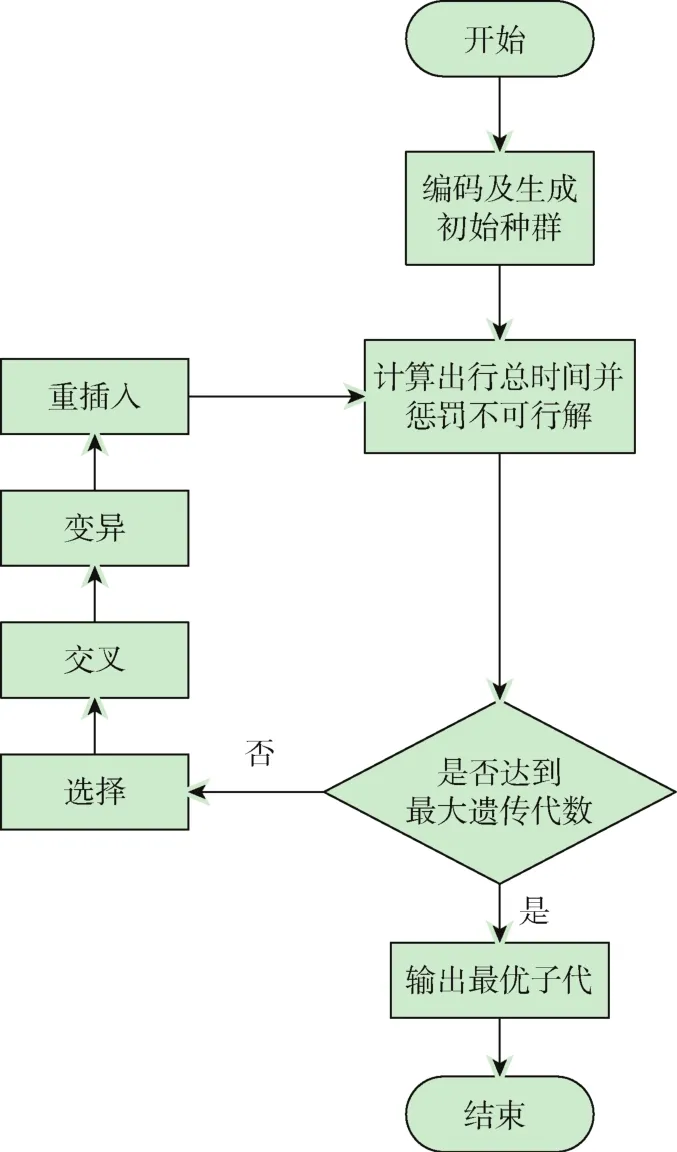
图8 遗传算法流程Figure 8 Flow chart of genetic algorithm

2.1 编码设计

合理的编码方式能够提高遗传算法的优化性能与效率，考虑到问题及相关模型的特点，如图9所示，算法中采用二进制编码与实数编码组合的方式进行染色体编码，具体过程如下：

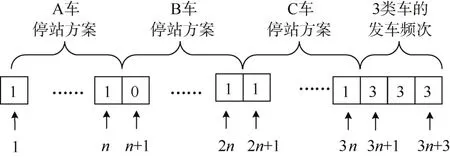
图9 编码示例Figure 9 Coding example

1) 将一个n车站，3类车辆的解编为一个3×(n+1)长度的染色体；

2) 前3n位染色体使用二进制编码，每n个位点分别代表1类车，其中1表示停站，0表示跳停；

3) 后3位染色体使用实数编码，表示3类车的小时发车频次。

2.2 算法步骤

设置遗传算法的初始参数：种群规模popsize，最大的遗传迭代次数maxgens，交叉概率pc，变异概率pm，代沟GGAP，惩罚数pe，当前代数generation=1。

2.2.1 步骤1：初始种群生成

1) 按照车站顺序依次生成停车方案：第i个车站的停站方案将在i，n+i，2n+i位点等概率随机填入(1，1，1)，(0，1，1)，(1，0，1)，(1，1，0)，从而能够保证每个站至少有两列车停靠；

2) 在3n+1至3n+3位点随机生成相等且满足初始满载率要求的发车频次；

3) 重复上述操作popsize次。

2.2.2 步骤2：遗传操作

通过选择、交叉、变异操作，生成子代新个体。为提高子代中可行解的数量，并保留优良父代个体不被破坏，将根据GGAP，保留一部分父代个体不参与交叉、变异，并在新子代生成之后重插入子代之中。

1) 选择。计算各父代染色体的总出行时间，取倒数为适应度，并对其中不可行解进行惩罚，降低适应度。根据GGAP值，按照轮盘赌的方式选择参与交叉变异的染色体。

2) 交叉。随机选择交叉位点，并按照交叉概率pc进行单点交叉。

3) 变异。随机选择两个停站位点，并按照变异概率pm进行变异。

4) 重插入。根据GGAP值，将父代中一定数量最优的染色体重插入子代之中，将子代数量补齐至popsize。

2.2.3 步骤3：终止操作

到最大的遗传迭代次数maxgens后，自动终止。

3 案例分析

基于上述构建的 A/B/C跨站停开行方案优化模型，以北京地铁6号线为例，分别以总出行时间最小和总在车时间最小为优化目标，通过与现有站站停模式下的乘客出行时间进行对比，从而验证A/B/C跨站停运营模式下乘客出行时间节省效果。

3.1 案例概况

如图10所示，北京地铁6号线从海淀五路居站至潞城站自西向东经过26个站，依次标记为1至26站。

图10 北京地铁6号线线路Figure 10 Route of Line 6 of Beijing Metro

以2018年10月某工作日10:00～11:00的客流OD数据为基础进行优化，该线路可用车底数为36列，现有站站停模式下发车间隔为 4 min，加减速损失时间为0.5 min。

3.2 计算结果

利用Matlab求解所构建的模型。参数标定如下：迭代次数为200，变异概率为0.1，种群规模为100。以下分别以总出行时间最小和总在车时间最小为目标，求解最优开行方案并进行对比。

3.2.1 以总出行时间最小为目标

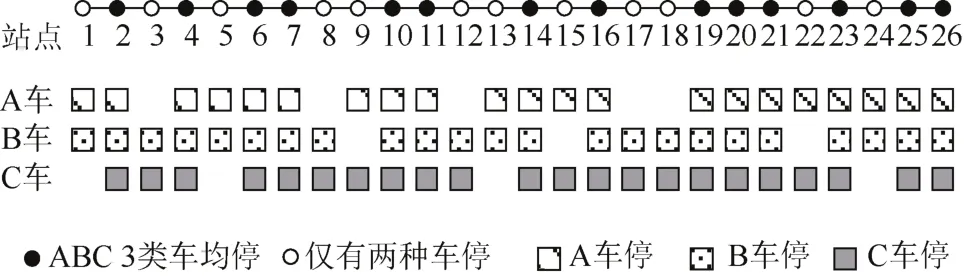
图11 以总出行时间最小为目标的停站优化方案Figure 11 Stopping optimization scheme to minimize total travel time

最优方案下，A、B、C 3种类型的车辆停站次数分别减少5次、3次和4次，总计跳停12个站。

如图12所示，与站站停方案相比，乘客总出行时间和总在车时间均有所降低，人均在车时间减少约1.19 min。此外，A/B/C跨站停最优方案下，每小时总停站次数减少60次，降低了停站带来的运营成本。

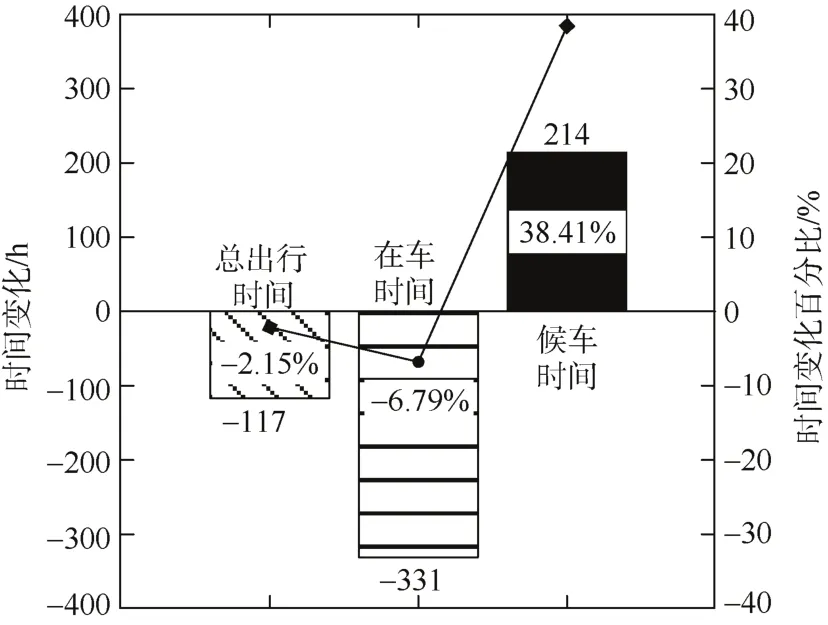
图12 以总出行时间最小为目标的优化方案效益Figure 12 Benefits of the optimization plan to minimize the total travel time

3.2.2 以在车时间最小为目标

为了方便与前一方案进行对比，假设始发站仍然按照A、B、C的顺序以4 min为间隔依次发车。以在车时间最小为目标进行优化，最优停站方案见图13。

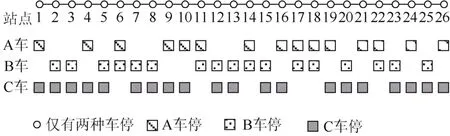
图13 总在车时间最小的停站方案Figure 13 The stopping plan with the shortest total on-board time

可见该目标下的总停车次数相较于前一场景明显下降，有利于进一步降低停站带来的运营成本。其中A、B、C 3种类型的车辆停站次数分别减少11次、9次和6次，所有车站中均有车辆跨站不停的情况。所需车底数为35辆，可节省1辆车底。

与前一场景相比，本优化方案下总在车时间下降更为明显，降低14.25%；由于跨站数量的增加，乘客所能选乘的车辆数减少，候车时间增加了868 h，最终使得总出行时间有一定上升，如图14所示。

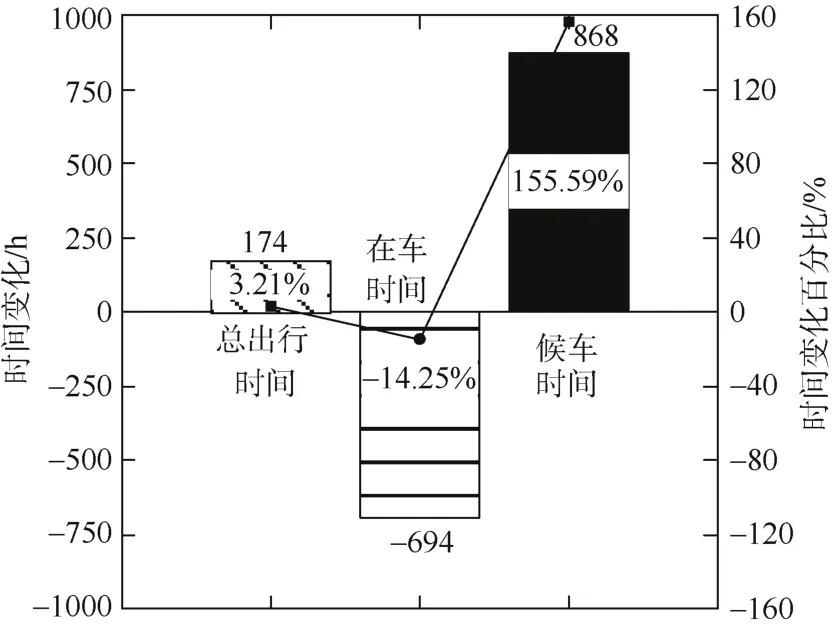
图14 总出行时间最小的停站方案时间变化Figure 14 Time change of the stop plan with the shortest total travel time

4 结语

1) 分析A/B跨站停运营特点的基础上，本文提出A/B/C跨站停模式。该运营模式的优点在于不仅可实现无越行下列车旅行速度的提高，而且所有乘客都可直达，无需换乘即可到达终点。

2) 根据可乘坐列车类型的不同，将乘客出行起讫点OD分为3类，分别给出了不同类型乘客的列车选择概率以及出行时间计算公式。

3) 构建了以出行时间最少为目标，以停站方案和发车频次为决策变量的混合整数规划模型，该模型适用于实际线路中开行方案优化问题。

4) 文中通过遗传算法设计对模型进行求解，并以北京轨道交通6号线实际数据为基础进行算例验证，有效证明了A/B/C跨站停运营模式对减少乘客出行时间以及运营成本的有效性。