列车运行工况对电力变压器直流偏磁影响的仿真分析

仰 枫，李春茂，郭裕钧，曹晓斌

（西南交通大学电气工程学院，成都 611756）

随着地铁建设的大力发展，地铁周边电力变压器出现直流偏磁现象越来越严重。对于地铁附近变电站变压器直流偏磁现象，国内外经过广泛研究，认为主要与地铁引起的地表电位分布有关。电位分布不同引起电力变压器发生直流偏磁，增加谐波含量，对电网设备产生多种危害。

地表电位方面，武汉大学建立地铁仿真模型，仿真分析了不同过渡电阻对钢轨电位影响[1]。西南交通大学根据理论公式推导出过渡电阻与杂散电流的关系，并对仿真模型进行改进[2-3]。文献[4-7]通过对地铁杂散电流建模，研究多列车同时运行下，钢轨纵向电阻对钢轨电位和杂散电流分布的影响。

文献[8]建立了双边供电模型，研究了钢轨过渡电阻对杂散电流分布的影响。国外学者首先研究杂散电流对埋地金属的腐蚀性关系，随着地铁的发展，也开始研究杂散电流对周边电力设备造成的影响[9-11]。

在直流偏磁方面，Dolara等[11]对比研究了直流励磁和交流励磁两种情况对变压器直流偏磁的影响；肖华对变压器直流偏磁现象进行研究，表明直流偏磁对变压器铁芯发热、运行噪声等影响较大[12]；文献[13]首先指出地铁运行产生的杂散电流会对变压器造成直流偏磁的影响；文献[14]明确了地铁杂散电流是城市电网主变压器直流偏磁的主要原因，并提出了相应的解决措施。但这些文献只针对单列车运行对变压器直流偏磁的影响，且影响机理尚不明确。为此，本文利用有限元软件建立了上下行列车的动态仿真模型，分析了列车运行在不同工况下其地表电位变化规律，通过电力系统仿真软件计算出相应位置变压器励磁电流畸变情况，为地铁周边电力变压器直流偏磁防治提供理论依据。

1 地表电位仿真及其影响因素

1.1 地铁对周边电力变压器的影响

变压器直流偏磁是指在变压器励磁电流中产生直流分量引起变压器铁心半周磁饱和，以及由磁饱和产生的一系列电磁效应[15]。由于钢轨过渡电阻不完全绝缘，钢轨泄漏电流在地表产生电位差，如果周边存在电力变压器，且中性点电位不相等时，会在线路中流过直流电，直流电流产生的磁通使得变压器饱和，进而出现直流偏磁，直流电流将从一台变压器中性点流进另一台变压器中性点，通过架空线路形成回路，一般为了充分利用电力变压器，变压器工作在铁芯饱和特性曲线转折点处，因此非常小的电压就可以使变压器发生直流偏磁。

地铁的钢轨对地不能达到完全绝缘，有部分钢轨回流电流会泄露至地下，称为杂散电流。该电流会对周边地表电位产生影响，当杂散电流大于某一阈值时，就会使得周边电力变压器产生直流偏磁。

1.2 数学模型

为了对列车上下行运行造成周边土壤电位畸变进行定量描述，本节建立钢轨—排流网—大地的电阻网络模型，模型基于以下假设：

1) 假设土壤均匀分布；

2) 假设列车以单边供电方式运行，列车牵引供电电流已知，分别为I1、I2，供电区间长度为L；

3) 假设在列车运行中，不存在容性或感性效应，可以用电阻网络模型等效。

模型中将列车和牵引供电站等效为电流源，建立的电阻网络模型如图1所示：

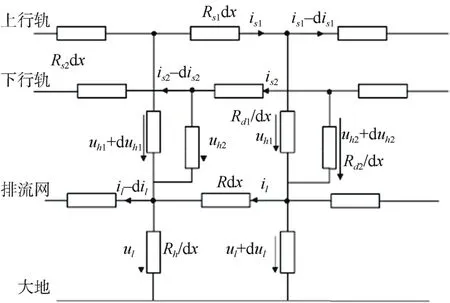
图1 上下行列车电阻网络模型Figure 1 The resistance network model of the outbound and return trains

图1中，Rs1、Rs2分别为上、下行钢轨的纵向电阻；is1、is2分别为上、下行钢轨的纵向电流，方向相反；Rd1、Rd2分别为上、下行钢轨对排流网的过渡电阻；Rl为排流网的纵向电阻；Rh为排流网对大地的过渡电阻；uh1、uh2分别为上、下行轨对排流网电压。根据基尔霍夫定律建立的微分方程如下：

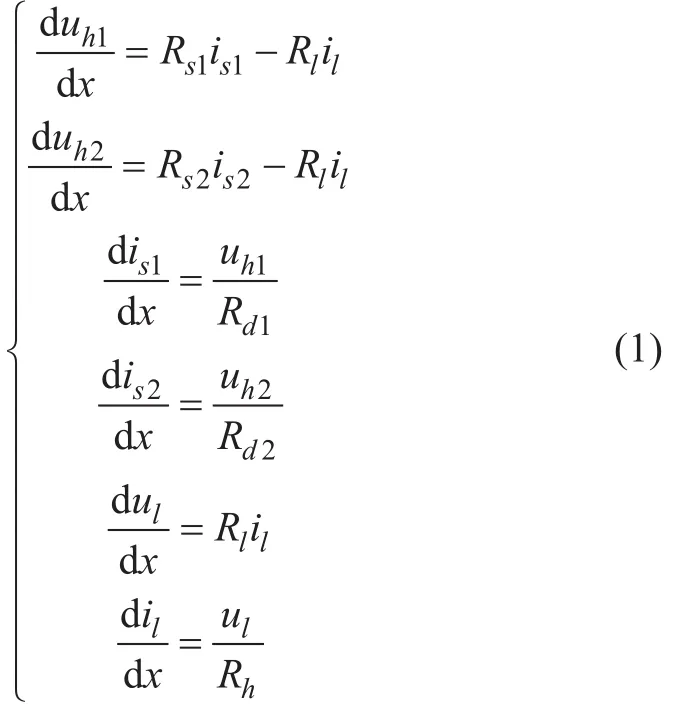
方程边界条件为：

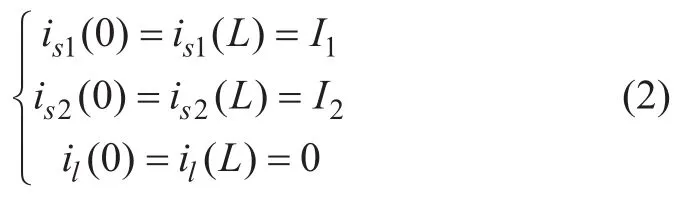
基于公式求解得到is1、is2、il，总的泄露电流为I1+I2-is1-is2-il。公式中可以看到，在考虑上下行列车运行时，泄露电流由两部分综合而成，变化情况更加复杂。

1.3 仿真建模

本节利用有限元软件对地铁系统建模，模型包括钢轨、轨枕、混凝土层、排流网等结构。由于钢轨结构对地表电位分布影响不大，将钢轨等效为圆柱导体并假设无穷远处电位为 0。钢轨下方放置轨枕、混凝土层、排流网结构。记区间左端地铁站为1号变电站，右端地铁站为2号变电站，列车A从1号变电站向2号变电站行驶，列车B从2号变电站向1号变电站方向行驶，如图2所示。

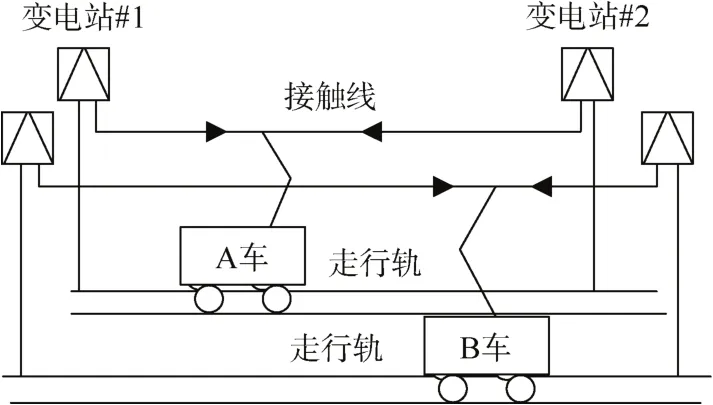
图2 列车运行示意Figure 2 Schematic of train operation

采用单一变量法，假设列车A状态不变，对比分析表1中的4种情况。

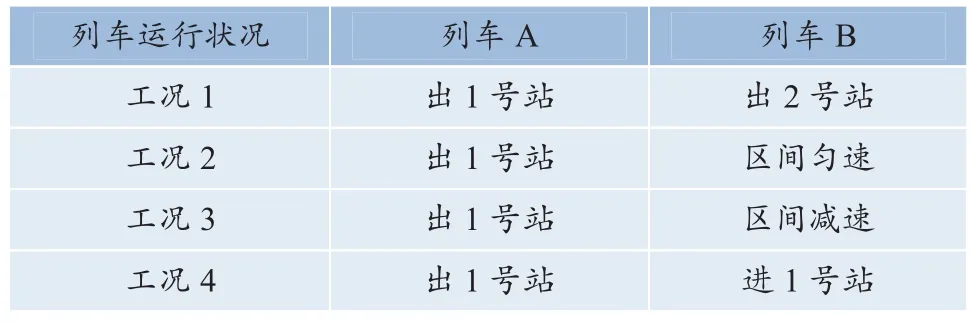
表1 列车运行情况假设Table 1 Assumptions of train operation

列车在不同状态运行时，其牵引电流也不相同，当列车出站时，电流上升并达到峰值，当列车匀速运行在区间中部时，电流保持在很小的值，用于克服摩擦力，当列车即将进站，列车牵引电流为负值，因此地表电位是时变函数。

2 结果分析

2.1 地表电位动态仿真

电力变压器的落点位置对变压器中性点电位差有重要影响，取地铁线路平行方向和垂直方向仿真电位进行对比，其中变电站1和变电站2区间长度为3 000 m，对比得到地表电位分布如图3～6所示。

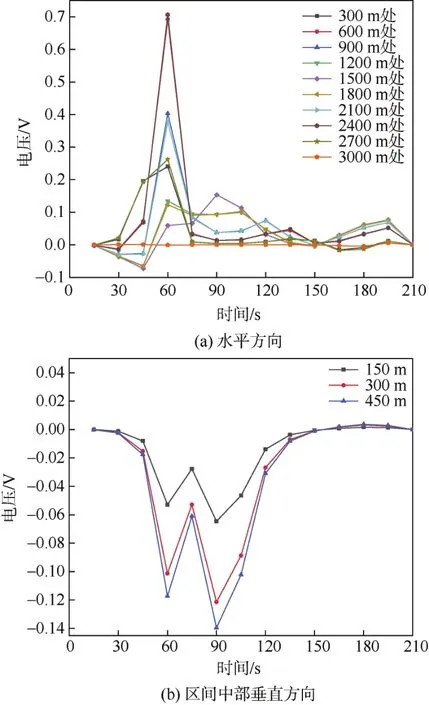
图3 工况1下地铁周边地表电位差Figure 3 Ground potential differences around the subway under working condition 1

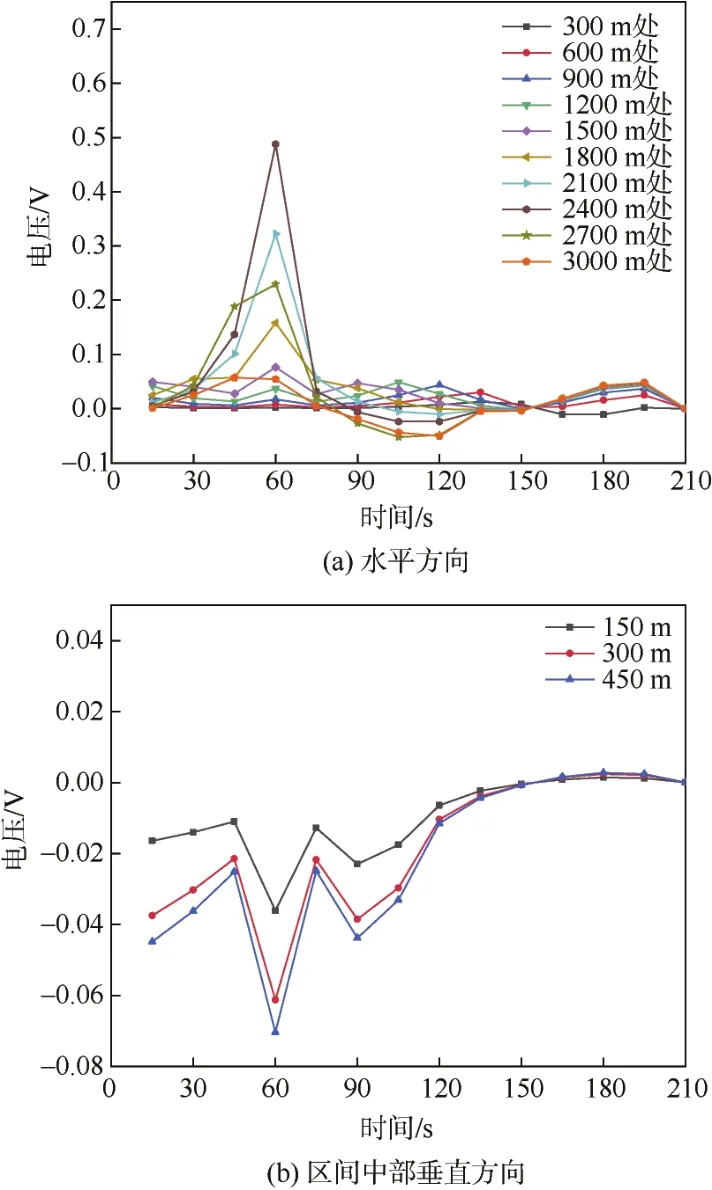
图4 工况2下地铁周边地表电位差Figure 4 Ground potential differences around the subway under working condition 2

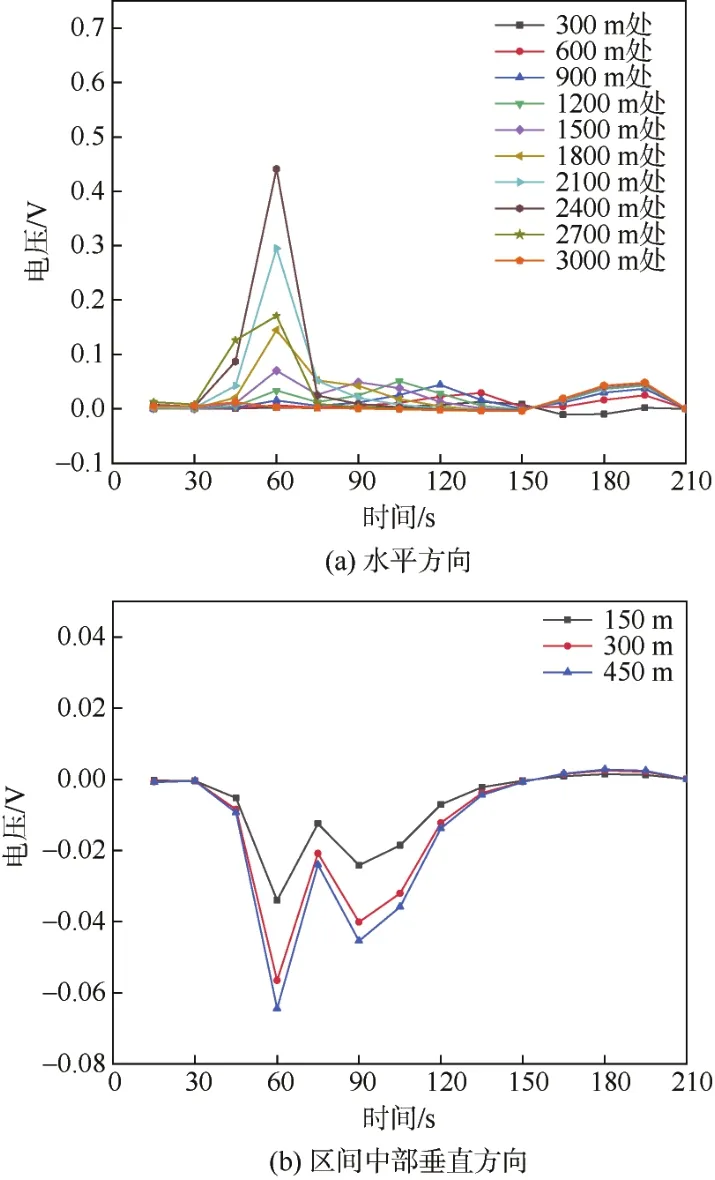
图5 工况3下地铁周边地表电位差Figure 5 Ground potential differences around the subway under working condition 3

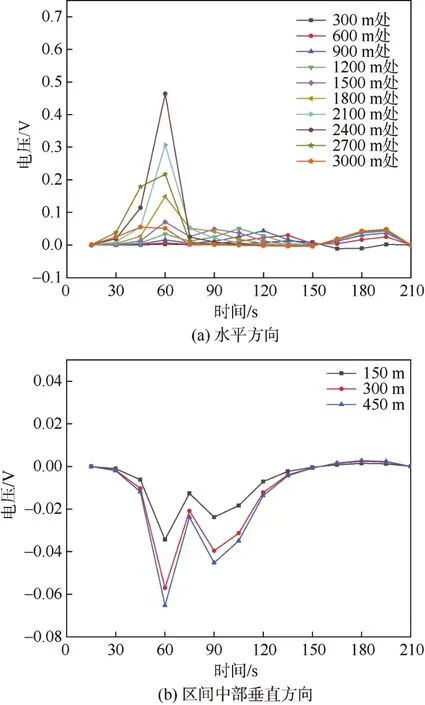
图6 工况4下地铁周边地表电位差Figure 6 Ground potential differences around the subway under working condition 4

列车在4种工况下，水平方向上均在距离地铁站2 400 m处达到峰值；垂直方向上，随着距离的增大，电位差也逐渐增大，但是变化幅值较小。当列车运行在工况2～4时，水平和垂直方向上幅值与列车运行在工况1时情况相比均明显减小，此外垂直方向上，受A车影响，首位端电位变化不再对称，且幅值明显低于对称运行。因此初步推测工况1下变压器直流偏磁最严重。

2.2 变压器励磁电流分析

利用电力系统仿真软件搭建变压器—传输线模型，设置变压器工作在饱和特性曲线转折点处，取上述4种工况下最大电压变化曲线作为电力系统仿真的输入(即水平沿线2 400 m处电位变化曲线)，仿真分析得到变压器励磁电流变化曲线如图7所示。

从图7中可以看到，当没有地铁通过时，变压器中性点不存在电位差，此时线路中没有直流分量，变压器励磁电流为正弦波，幅值为0.05 A，磁通也为正弦波；当列车运行在工况1下，励磁电流畸变情况严重，电流最大可达0.15 A；相对于工况4(即单列车运行时)，明显高于单列车运行状态。因此，上下行列车运行相比于单列车运行对周边变压器直流偏磁情况更加严重。对励磁电流选取第一个周期进行傅里叶分析，结果如表2所示，表中正常情况下畸变率仅有0.23%；而在工况1下，由于地表电位幅值变化较大，励磁电流畸变率达到了7.89%；当处于工况3和工况4时，励磁电流畸变率近似不变，且工况3略低于工况4，这是因为列车制动运行，导轨中流过负向电流对地表电位的削弱作用，因此地表电位幅值较单列车运行时低。

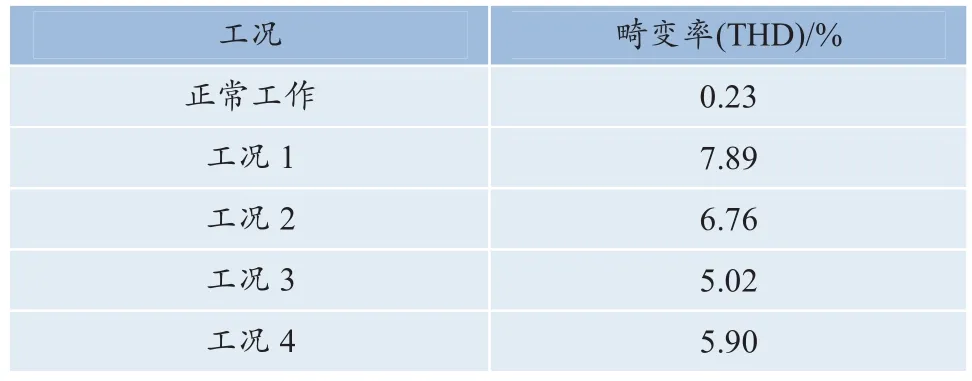
表2 励磁电流畸变率Table 2 Distortion rate of excitation current

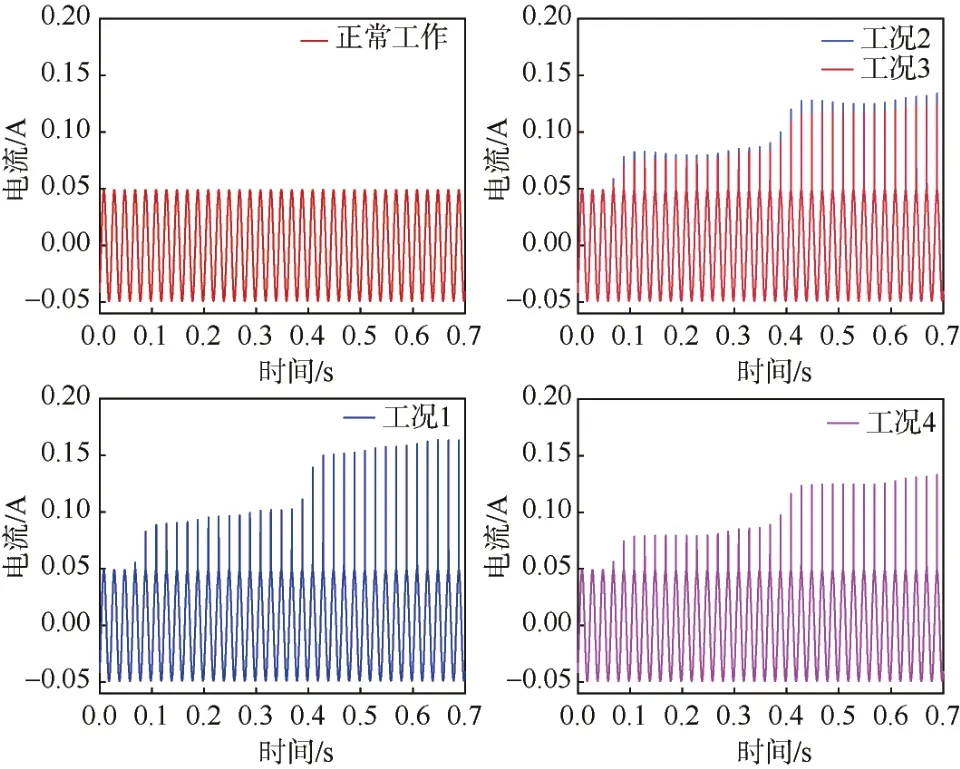
图7 2400 m处变压器励磁电流变化曲线Figure 7 Variation curve of transformer excitation current at 2 400 m

3 结语

本文建立上下行列车有限元仿真模型以及变压器-传输线仿真模型，通过仿真得出当上下行的两列列车同时出站时，地表电位峰值达到最大，对应变压器直流偏磁情况最为严重；当其中一辆列车加速运行，另一辆列车减速运行时地表电位峰值最小，直流偏磁相对较轻，此外相对于单列车运行时，双列车运行的危害较大。因此，为保障地铁周边变压器正常运行，应调整地铁运行时间，避免地铁同时进站造成变压器直流偏磁，从而影响正常用电。