地下富水城市的地铁车站对地下水渗流影响探讨

高 扬 ，王 鑫，张 康，雷炳霄 ，曾纯品

（1. 山东省地质矿产勘查开发局八〇一水文地质工程地质大队(山东省地矿工程勘察院)，济南 250014； 2. 济南轨道交通集团有限公司，济南 250100；3. 山东省地下水环境保护与修复工程技术研究中心，济南 250014）

近年来，随着大量地下空间工程的修建，因其对地下水渗流条件的改变导致环境问题不断凸显。例如，宿庆伟对济南某小区周边地下水位上升的原因及水文地质条件的变化特征的调查表明，由于人类活动的影响，该小区周边的水文地质条件发生了较大变化，小区周围由原来的径流排泄区慢慢转变为一个小型的蓄水区，造成这里地下水位大幅上升，并对构筑物产生了不利影响[1]。陈丽影、时晓以成都国际机场为例，通过数值模拟分析地下空间的开挖对地下水环境的影响，结果表明：地下空间结构在建设期间及建设完成后，地下水的渗流条件发生改变，生成新的局部分水岭，新的补径排关系确立[2-3]。Ni 等通过研究临江城市的地下水位变化，得出城市地下空间建设是水位变化重要原因的结论[4]。Lee 等通过对韩国大邱广域市地下水位的长期监测，构建模型，得出地铁建设会影响周边地下水水位变化的结论[5]。地下工程结构对地下水产生影响，可能引发工程与环境问题，如图1所示。 发对地下水环境的影响展开研究[10]。郑品等通过室内试验，对比了有物体阻挡和没有物体阻挡下地下水渗流情况的变化[11]。可见，地下空间工程建设对地下水环境的影响，正在引起越来越多学者的关注。笔者将基于一维渗流理论，通过对修建地铁车站前后的地下水渗流特点进行分析，探索地铁车站对地下水渗流的影响规律，以期得到受车站阻隔作用影响的地下水位壅高及流量解析式，相应成果可为地下富水城市的地铁车站建设提供参考依据。

1 渗流影响分析

图1 地下结构对地下水环境的影响[6] Figure 1 Influence of underground structure on groundwater environment[6]

1.1 未建地铁车站时的地下水渗流分析

未建地铁车站时，可根据拟建车站位置的勘察结果及地层条件，概括为如下基本条件及假设。

1) 假设沿地下水流动方向上有观测孔A 及观测孔B，观测孔A 测得的水位高度为h1，观测孔B 测得的水位高度为h2，两孔之间地下水的流动满足由观测孔A 流向观测孔B 的条件，且为潜水流；

2) 隔水层均质同向，底部隔水层水平；

3) 由于城市内道路硬化等因素，不考虑渗流段的大气降雨入渗补给的影响，雨季地下水流量的变化主要由洪水期时观测孔的水位高度的变化体现；

4) 两观测孔间的地下水流动为一维流，且是渐变流并趋于稳定。

根据上述条件建立地下水渗流模型，如图2 所示。

工程建设与地下水运动的影响是互馈的，地下水会对地下空间结构造成影响，同时地下结构施工对地下水的运动状态也存在一定的影响[7-8]。许劼等以南京地铁为工程背景，分析了玄武湖水下隧道施工对地下水排泄的影响机理[9]。曹洪等基于有限元法，提出了考虑阻水结构的模拟方法，并对广州城区地下空间开

图2 两观测孔间的潜水运动 Figure 2 Schematic of diving movement between two observation holes

由于城市内大多数情况下水位的变化幅度不大，故可根据上述模型忽略地下水渗流过程中的竖向速度分量vz，地下水渗流过程水位的降低可视为由于地层的阻隔作用而引起的势能损失。

根据上述条件和假设，可得如下数学模型：

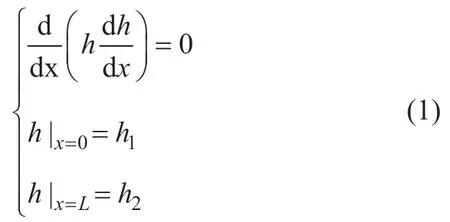
对式(1)进行积分求解，可得观测孔A、B 之间任意一点的地下水位，即

式中：L 为两观测孔间距离，m；x 为拟求水位处距观测孔A 的距离，m；h1为观测孔A 的水位高度，m；h2为观测孔B 的水位高度，m。

对式(2)进行求导，可得h 关于x 的函数关系，即

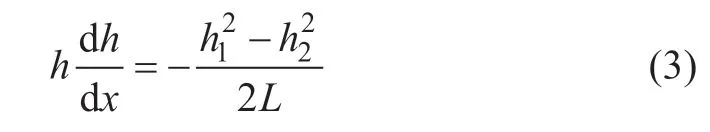
引入达西定律，可得任意断面处的单宽流量公式，即

式中：K 为渗透系数，m·d-1；qx为与观测孔A 距离为x 处的单宽流量，m2·d-1。

将式(3)代入式(4)，可得

式(5)即是流经观测孔A、B 之间任意断面的单宽流量公式。

1.2 地铁车站对地下水渗流影响机制分析

1.2.1 地铁车站基本条件

1) 由于地铁车站基坑一般采用地连墙或止水帷幕等结构措施，故假设地铁结构外端为隔水边界。

2) 通常车站长度为300～500 m，与中粗砂等含水层的影响半径R 相当，且由于地铁车站两端一般为直径6 m 的盾构区间，盾构施工时采取注浆等措施对原渗水通道有堵塞作用，透水能力大幅降低，故可以忽略地下水遇车站结构时产生的绕流问题，因此将车站两端盾构区间与车站结构共同视为隔水边界。

3) 车站结构建成后与建成前相比，车站外的地层结构未发生变化，流经车站结构处的水流量不变。

1.2.2 地下水壅高分析

如图3 所示，为解决地铁车站的阻水作用对地下水渗流带来的影响，不妨再作如下分析。

图3 地铁车站结构附近潜水流镜像关系 Figure 3 Schematic of mirror relationship of a phreatic flow near subway station structure

1) 设观测孔B 位于迎水面车站结构处，且水位高度为h2；观测孔A 位于车站外迎水方向上，且水位高度为h1；地下水流动，满足由观测孔A 流向观测孔B的条件。

2) 根据镜像原理，可假设车站结构背水面一侧有一虚观测孔A′，其距离与观测孔A 到观测孔B 的距离相同；水位与观测孔A 相同，都是h1；地下水流动，同样也满足由观测孔A′流向观测孔B 的条件。

3) 根据叠加原理，由于车站结构的隔水作用，则车站结构处(观测孔B 处)的地下水位受到由观测孔A流向观测孔B的流量与由观测孔A′流向观测孔B的流量的叠加影响。

根据以上假设，由观测孔A 流向观测孔B 的流量q1与由观测孔A′流向观测孔B 的流量q2大小相等，方向相反，故实际区域与镜像区域两侧的流量叠加之后，其结果为

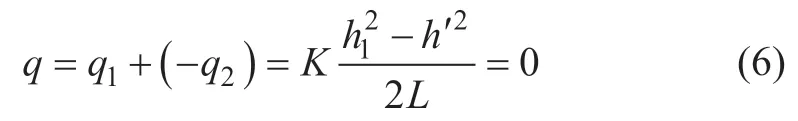
由式(6)可知，受到地铁车站阻水作用影响后，观测孔A、B 之间任意断面的地下水流量为0。此时，观测孔B 的地下水位高度与观测孔A 的地下水位高度相同，即

因地铁车站隔水作用产生的水位壅高为

式中：h 为车站建成后车站结构处的水位高度，m；Δh为考虑地铁车站阻水作用后的围护结构处的水位壅高值，m；h1、h2为地铁车站建设前观测孔A、B 内的水位高度，m。

根据式(8)可知，受到地铁车站阻水作用时，地下水流将会产生壅高，其壅高值与观测孔A 点的位置以及观测点A 处的水位高度有关。

为尽可能准确地得到地下水位的壅高值，应将观测孔A 的位置，设置于迎水一侧与地铁车站相距地层影响半径R 处。然而，在工程实践中，由于场地条件的限制，水位观测孔的位置不可能恰好位于其影响半径处。为解决这个问题，可引入水力坡度的概念，即在水流方向上的两个观测孔内的水位差与其距离之比，即

式中：h1、h2为勘察期间水流方向上的任意两观测孔内的地下水位，m；L0为两观测孔的距离，m。

由勘察孔之间的水力坡度，可得迎水一侧与地铁车站相距地层影响半径R 处的水位差，有

根据式(10)，可以在勘察阶段，根据研究区沿水流方向上任意两勘察孔的观测水位及地层条件，即可求得受拟建地铁车站阻隔作用后的地下水位最大壅高值。

1.2.3 抗浮设防水位分析

由前述分析可知，当地下水流遇到地铁车站的阻隔作用时，会产生一定的水位壅高值，车站抗浮水位应取上述基于长观水位及降雨量资料的抗浮设防水位值与考虑地铁车站阻隔作用的地下水壅高值之和，即

式中：Hf为考虑地下水雍高影响的抗浮设防水位建议值，m；Ho为基于长观水位及降雨量资料得到的抗浮水位建议值，m；Δh 为按照笔者所述方法推导出的考虑地铁车站阻隔作用的地下水位壅高值，m。

1.2.4 地下水流量分析

若使车站结构对地下水渗流的影响最小，即不产生壅高等问题，需维持与原地质结构相同的渗流条件，即受地铁车站阻隔作用的地下水流量与未建地铁车站时流经此断面的地下水流量相同。

未建车站时，原地质条件下的单宽流量可采用式(5)求得，因此受地铁车站阻隔作用的地下水流量为

式中：Q 为受地铁车站阻隔作用的地下水总流量，m3·d-1；B 为车站总长度，m。

2 工程实例分析

2.1 车站工程概况

济南某地铁车站沿东西走向敷设，全站全长345.62 m，采用明挖法施工，地连墙支护结构。

综合室内渗透试验和现场钻孔抽水试验的结果，结合工程经验，基坑地下水控制所需的各层岩土的渗透系数可按表1 中的建议值选用。地连墙进入19-3 中风化闪长岩地层。

表1 各层岩土渗透系数建议值 Table 1 Recommended values of the permeability coefficient of each layer

2.2 地下水位壅高值

根据勘察期间水位测量的结果，运用绘图软件，绘制的未建车站时拟建车站位置处的流网图，见图4。

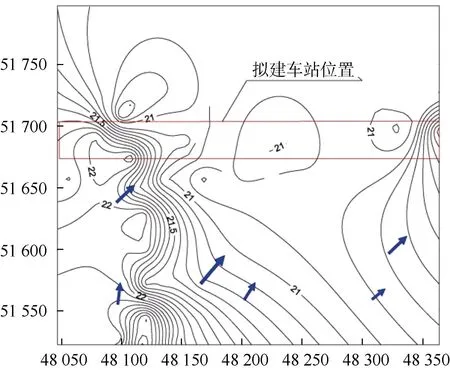
图4 济南某地铁车站建设前的地下水流网图 Figure 4 The flow-net of groundwater before the construction of a subway station in Jinan

可以看出，拟建地铁车站为东西向。未建地铁车站时，地下水流向为SW 至NE，拟建地铁车站与地下水流向近似正交关系；地铁建成后，受地铁车站的阻隔作用，新的局部分水岭将生成，地下水渗流条件发生改变，地下水的补径排关系将重新确定。

为简化计算，可将图4 所示受车站阻隔作用的地下水流近似看作南北向流动，则可选取南北向的12-12’地质剖面作为本次计算剖面，取隔水底板标高为-8 m，A 点取C08XZ45 号孔，A 点水位标高为h1=22.92 m；则B 点取C08XZ3 号孔，B 点水位标高为h2=20.68 m。

AB 两观测孔间的直线距离L0=187 m。

含水层渗透系数K，本次取根据C08XZ7 号孔土层参数计算的含水层综合渗透系数，即K=4.752× 10-3cm/s。其渗透系数与粉砂相当，影响半径可取经验值R=50 m。

将上述参数代入式(11)，解得受车站结构影响的地下水壅高值，如表2 所示。

表2 济南某地铁车站地下水壅高计算 Table 2 Groundwater backup calculation of a subway station in Jinan m

由于车站建设前与建成后地下水位测量的时间不一致，难以采用水位直接进行对比，因此采用水力坡度J 作为参考指标。车站建设前原始水力坡度、车站建成后实测地下水水力坡度与计算值的对比关系如表3 所示。

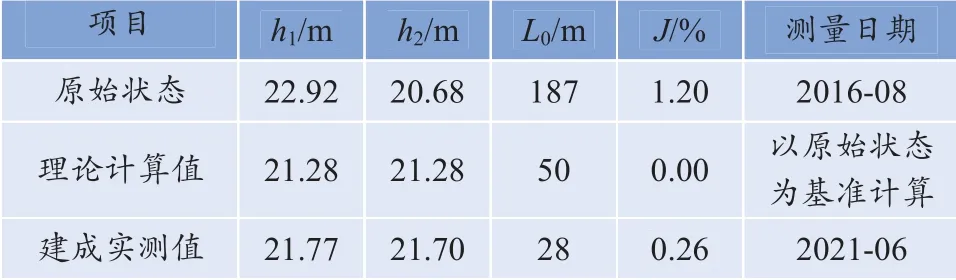
表3 水力坡度原始值、实测值与计算值对比关系 Table 3 Comparison of original, measured and calculated value of hydraulic gradient

可以看出，车站建成后受到地铁车站的阻隔作用，水力坡度会明显减小，虽然仍会有一定的水力坡度，但这是由于理论计算时忽略了地下水从车站结构两侧绕流情况而引起的。总的来说，实测值与理论值的拟合度较高，该理论值的计算结果相对较保守，所以可作为设计参考依据。

2.3 抗浮设防水位

本工点场地的地下水稳定，水位埋深0.7～3.7 m，高程介于19.94～22.92 m 之间，勘察期间(2016 年8 月)属年较高水位期，基于3～5 年长观水位及降雨量资料(见图5)，可按照文献[12]提出的方法得到抗浮设防水位建议值(见表4)。 根据式(11)，考虑地铁车站对地下水渗流阻隔作用，抗浮设防水位为Hf=22.92+0.60=23.52 m，故本次抗浮设防水位的建议值取23.52 m。

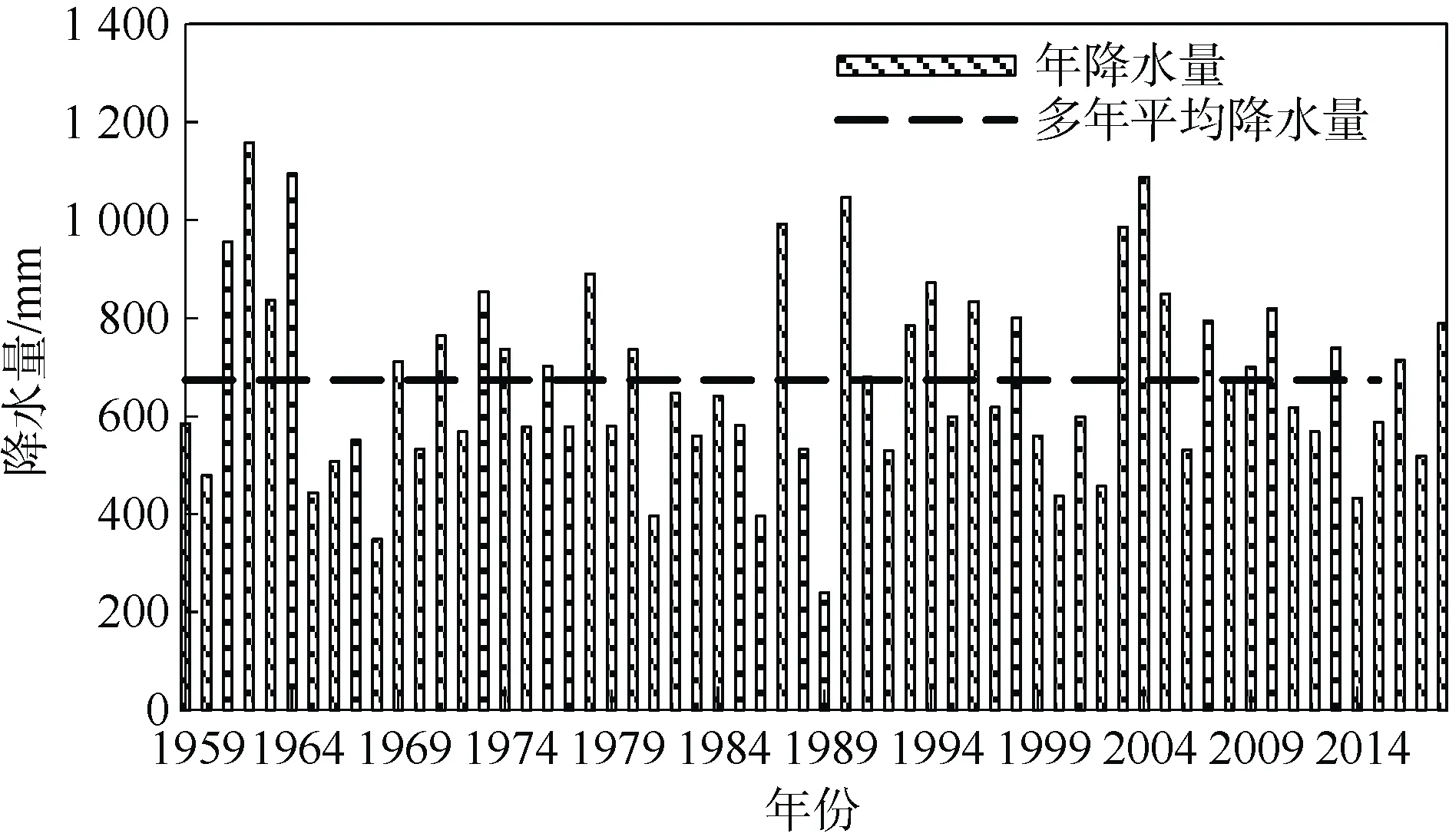
图5 济南市1956—2018 年降雨量 Figure 5 Rainfall histogram of Jinan City from 1956 to 2018

表4 基于观测资料得到的抗浮设防水位一览 Table 4 Anti-floating water level based on observation data m

2.4 地下水流量

地下水产生壅高的原因是地铁车站阻隔了含水层中正常的地下水渗流，根据式(5)求得未建车站时流经此位置的单宽流量q=1.5 m2/d；车站东西总长度约350 m，受地铁车站阻隔作用的总流量为Q=qB=1.5× 350=525 m3/d。因此，若想地下水渗流过程中不受地铁车站阻隔影响产生壅高，则需采取措施排导的地下水流量为525 m3/d。

3 结语

1) 根据一维渗流理论，对未建地铁车站时的地下水渗流情况进行了分析，并结合镜像原理及叠加原理，分析了地铁车站对地下水渗流的影响机制，得到了受地铁车站阻隔作用的地下水壅高值，以及地下水流量的解析式。

2) 运用本研究得到的理论公式，分析了济南某地铁车站因受车站阻隔作用引起的地下水位壅高、地下水流量变化等，并提出了考虑地下水壅高的抗浮设防水位建议值。

3) 车站处受阻隔作用而产生地下水壅高值，与含水层的影响半径、水力坡度等有关。在实际工作中，当遇到具有一定的水力坡度的强透水含水层时，地铁车站建成后可能产生的地下水壅高应当引起工程人员的重视。