玉米田桃蛀螟幼虫的空间分布型与抽样技术

李少华，王云鹏，王荣成，尹萍，李向东，郑方强

玉米田桃蛀螟幼虫的空间分布型与抽样技术

山东农业大学植物保护学院，山东泰安 271018

【目的】桃蛀螟（）是重要的农业害虫，近年来在我国黄淮海玉米产区危害日益严重，已成为玉米安全生产的威胁之一。空间分布型是昆虫种群的重要生态属性，研究桃蛀螟幼虫在玉米田的空间分布型，明确其在玉米田的空间分布特征，为桃蛀螟的田间抽样计划制定、预测预报和有效防治提供科学依据。【方法】利用传统统计学（聚集度指标、Taylor幂法则和Iwao回归模型）和地统计学方法研究玉米田桃蛀螟幼虫种群的空间分布型。基于Iwao回归模型确定桃蛀螟幼虫的理论抽样数，通过序贯抽样技术得到不同允许误差（=0.1、0.2、0.3）和经济阈值（0=0.5、1、1.5、2头/株）下的最大理论抽样数。【结果】两种统计学方法的结果均表明桃蛀螟幼虫种群在玉米田的空间分布型属于聚集分布。聚集度指标分析表明桃蛀螟幼虫的分布型为聚集型；Taylor幂法则结果显示桃蛀螟幼虫种群为聚集分布，且聚集强度随种群密度的升高而增加；Iwao回归模型证明桃蛀螟幼虫的空间分布型属于聚集分布，且为一般的负二项分布。根据半方差函数模型参数，确定桃蛀螟幼虫种群的最优拟合模型为球型、指数型和线型，表明空间分布型为聚集型；通过Kriging插值法分析得到桃蛀螟幼虫种群的三维和二维空间分布图，其聚集中心主要分布在田块边缘。基于Iwao回归模型抽样技术明确了桃蛀螟幼虫在置信概率=2，不同平均密度=0.5、1、2、3、4、5、10、15时的理论抽样数。进行序贯抽样确定了最大理论抽样数，在=2，=0.1、0.2、0.3时，当0=0.5头/株，最大理论抽样数分别为3 417、854和380株；当0=1头/株，最大理论抽样数分别为1 717、429和191株；当0=1.5头/株，最大理论抽样数分别为1 150、287和128株；当0=2头/株，最大理论抽样数分别为867、217和96株。【结论】桃蛀螟幼虫种群的空间分布型为聚集分布中的负二项分布，聚集中心主要分布在田块边缘。基于序贯抽样确定的理论最大抽样数可用于指导玉米田桃蛀螟幼虫的监测和防治。

桃蛀螟；聚集度指标；地统计学；空间分布型；抽样技术

0 引言

【研究意义】桃蛀螟（）是一种分布广泛的多食性钻蛀性害虫，已知寄主植物达100余种，除玉米、高粱、向日葵、蓖麻等大田农作物和经济作物外，还危害桃、板栗、石榴、苹果等果树以及松、杉、桧柏和臭椿等林木[1-2]。近年来桃蛀螟在我国黄淮海地区夏玉米上危害日趋严重，以幼虫蛀食玉米雌穗，引发多种穗腐病，严重影响了玉米的产量和品质，已对玉米的安全生产和食品安全构成了威胁。空间分布型（也称空间格局）是物种在一定空间的扩散分布形式，是昆虫种群重要的结构特征之一，其分布的形式由物种自身的生物学特性和/或生境条件所决定[3-4]。研究昆虫空间分布型不仅可以揭示昆虫在空间的分布特性，还能为昆虫在田间的抽样提供科学基础。确定昆虫空间分布型有两种方法，一是传统统计学的方法（频数法和聚集度指标法），另一个是现代统计学中的地统计学方法。因此，研究玉米田桃蛀螟幼虫种群的空间分布型，可以进一步明确桃蛀螟幼虫在夏玉米田的发生、栖息和分布，对于桃蛀螟幼虫种群田间抽样方法的确定以提高抽样精度并准确估计其种群数量具有重要理论和实践意义，同时可为该害虫的监测和有效防治提供理论依据。【前人研究进展】国内外学者对昆虫种群的空间分布型进行了大量研究，明确了许多昆虫的空间分布特征，例如棉铃虫（）[5-6]、麦长管蚜（）[7]、白背飞虱（）[8]和红脂大小蠹（）[9]等。利用地统计学方法，同时研究害虫及主要天敌的空间分布型，还可以反映出它们的空间跟随关系，如Park等[10]对玉米田玉米蚜（）与其天敌瓢虫空间分布的研究和赵静等[11]对烟田烟盲蝽（）及其天敌蜘蛛空间格局的研究，都发现天敌与其猎物害虫有很好的同域分布。利用传统统计学方法研究昆虫的空间分布型，最大的用途是基于许多聚集度指标应用于昆虫的田间抽样，能节省抽样时间和成本，特别是利用序贯抽样并依据经济阈值来指导害虫的防治[3]，如对马铃薯甲虫（）[12]和草地贪夜蛾（）[13-14]空间分布型及抽样技术的研究。目前，关于桃蛀螟的空间分布型与抽样技术已有报道。吴立民[15]对部分春玉米田和夏玉米田桃蛀螟幼虫的分布型及抽样技术进行了研究，表明呈聚集分布中的核心分布，提出了相应的序贯抽样表；周洪旭等[16]对玉米收获后茎秆中桃蛀螟越冬幼虫的分布型进行了测定，发现呈聚集分布中的负二项分布；陈炳旭等[17]对板栗上桃蛀螟幼虫的分布型进行了研究，证明是聚集分布中的负二项分布；郝立武[18]对山东泰安夏玉米田桃蛀螟幼虫空间分布型及动态进行了研究，结果呈现随机-聚集-随机的动态空间格局；王其武[19]在山东无棣进行了夏玉米田桃蛀螟幼虫空间分布型和田间抽样技术研究，发现调查的前期多属于随机分布，后期属于聚集分布。然而，前人对桃蛀螟幼虫分布型的研究，或缺乏地统计学数据的分析[15-16]，或集中在同一玉米田块进行研究[18-19]。基于昆虫空间分布型的研究，一般需要多块田的调查数据分析，才能更好地反映昆虫的空间分布特征。【本研究切入点】本研究选择多块夏玉米田，在桃蛀螟幼虫发生危害盛期进行调查，基于传统统计学（聚集度指标法）和地统计学方法同时分析不同玉米田桃蛀螟幼虫的空间分布型，并基于传统统计学方法进行桃蛀螟幼虫田间抽样技术研究。【拟解决的关键问题】利用传统统计学和地统计学方法分析多块玉米田桃蛀螟幼虫种群的空间分布型，基于Iwao回归模型建立其理论抽样数和序贯抽样模型，以期为玉米上桃蛀螟幼虫的田间抽样计划制定、预测预报和有效防治提供科学依据。

1 材料与方法

1.1 试验地概况

试验在山东农业大学植物保护学院实验站（36°10′0″N，117°9′18″E）和农学院玉米试验田（36°9′40″N，117°9′26″E）进行，选取的10块玉米田面积均不少于667 m2，除第1块和第10块玉米田为东西向外，其他田块均为南北向。调查期间玉米田未使用化学杀虫剂，只进行常规的田间管理。

1.2 抽样方法

调查时间为2017年8月30日至9月17日和2018年9月12日，既是泰安市桃蛀螟成虫发生盛期，也是桃蛀螟幼虫发生危害关键时期。采用网格取样法（4株×4株），每样点16株，每块玉米田根据地块大小不同，所取样方36—105个不等。每块田采用均匀布点取样并测量样点之间的距离，记录每样点玉米植株的方位及其对应雌穗上的桃蛀螟幼虫数量。每块玉米田均调查1次。

1.3 数据分析

1.3.1 传统统计学分析 利用DPS软件（7.05版）计算每块田抽样样方中桃蛀螟幼虫密度均值（）、方差（2）、平均拥挤度（*）、丛生指数（）、聚块指数（*/）、久野指数（C）和扩散系数（），据此分析桃蛀螟幼虫在夏玉米田的空间分布型，空间分布型的聚集度指标模型和判定标准参见丁岩钦[3]和唐启义[20]；基于桃蛀螟幼虫密度均值（）、方差（2）或平均拥挤度（*）分别拟合Taylor幂法则方程2=am或lg2= lg+lg和Iwao回归方程*=+，通过模型不同系数的组合确定空间分布型[3,21-24]。

1.3.2 空间格局的地统计学分析 采用地统计学中的半方差函数[25]，公式：

式中，（）是的半方差估值，（）是的所有点的配对数，（x）和（x+）分别是样点x和x+h的变量值。

地统计学中用来拟合空间变异曲线的理论模型有球状模型、高斯模型、指数模型、线性有基台值模型和线性无基台值模型等。在拟合过程中，根据决定系数2、残差平方和、块金值0、基台值0+、变程和空间结构比0/（0+）确定最优拟合模型。其中，块金值0反映区域化变量内部随机性的可能程度，基台值0+反映变量变化幅度的大小，变程反映区域化变量的影响范围或空间依赖性的大小，空间结构比0/（0+）反映空间变异的随机程度。一般当该比值小于25%时，表明变量具有强烈的空间相关性；介于25%—75%，表明变量具有中等程度的空间相关性；大于75%时，表明变量的空间相关性很弱[8]。

所有数据均用Matlab 7.0进行正态分布检验，不符合正态分布的数据用GS+3.1.7软件进行对数正态转换，转换后若最小值为负，调整补偿值为1，使其不小于0。采用Kriging插值法进行分析，绘制三维和二维图直观反映桃蛀螟幼虫种群真实的田间分布情况。

1.3.3 抽样技术分析 根据理论抽样原理[3,24,26]，建立理论抽样数模型：=(/)2[(+1)/+(-1)]。其中，为最适抽样数，为允许误差，为期望值的置信概率，为平均虫口密度，和为回归方程*=+的参数。

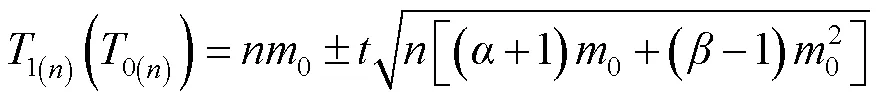
2 结果

2.1 桃蛀螟幼虫种群空间分布型的传统统计学分析

2.1.1 桃蛀螟幼虫种群的聚集度指标分析 根据玉米田桃蛀螟幼虫种群的聚集度指标（表1）可知，10块玉米田桃蛀螟幼虫种群的丛生指数（）、聚块指数（*/）和扩散系数（）均大于1，久野指数（C）值均大于0，说明桃蛀螟幼虫在玉田间的空间分布型为聚集分布。其中，田块1、2、5和6的平均拥挤度（*）较大，表明桃蛀螟幼虫在该田块的个体拥挤程度较高；田块8和10的平均拥挤度（*）较小，说明桃蛀螟幼虫在该田块的个体拥挤程度较低。

2.1.2 Taylor幂法则 基于表1数据，经拟合，得Taylor幂法则模型为lg2=0.262+1.308lg（=0.901，＜0.01）。由于lg=0.262＞0，且=1.308＞1，基于模型的判定标准，说明桃蛀螟幼虫种群为聚集分布，且聚集强度随种群密度升高而增加。

2.1.3 Iwao回归模型 根据表1数据，经拟合，得Iwao回归模型*=3.251+1.041（=0.996）。由于=3.251＞0，说明桃蛀螟个体间相互吸引，分布的基本成分是个体群；由于=1.041＞1，说明基本成分为聚集分布。基于空间分布型判定标准，桃蛀螟幼虫的空间分布型属于聚集分布，且为一般的负二项分布。

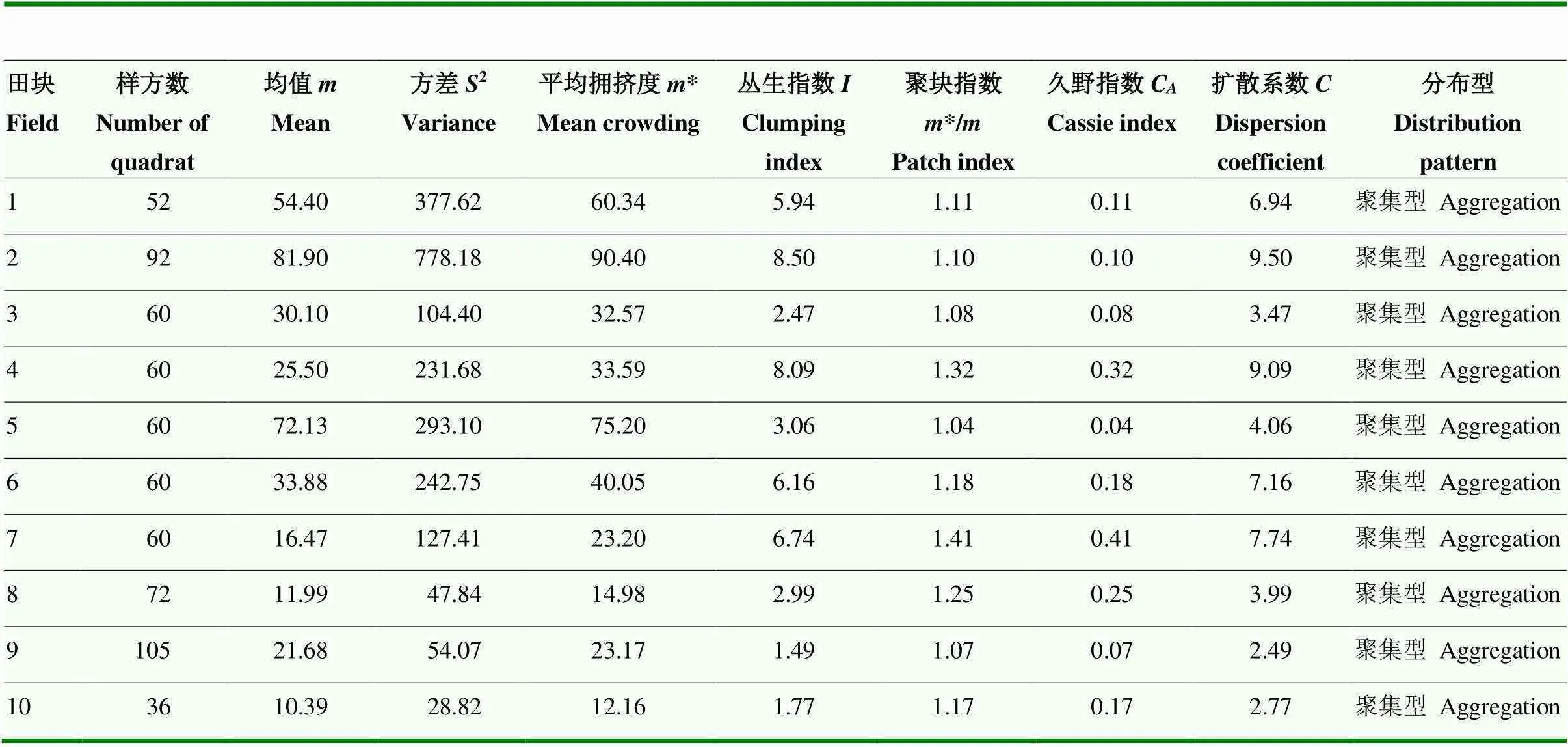
表1 桃蛀螟幼虫种群的聚集度指标

2.2 桃蛀螟幼虫种群空间格局的地统计学分析

根据10块玉米田桃蛀螟幼虫种群半方差函数的参数及其最优拟合模型，确定空间分布型均为聚集型（表2）。其中，田块1、3、4和9的半方差函数模型为指数型，田块2、5、6、8和10的半方差函数模型为球型，田块7的半方差函数模型为线型。块金值0在0.10—129.00，田块2的块金值最大，为129.00，说明该田块桃蛀螟幼虫种群引起变量随机变化的程度最大；田块4和6的块金值最小，均为0.10，表明这两块田桃蛀螟幼虫种群引起变量随机变化的程度最小。基台值0+在0.43—774.70，田块2的基台值最大，为774.70，表明该田块变量的变化幅度最大；田块7基台值最小，为0.43，说明该田块变量的变化幅度最小。变程为1.44—17.56 m，空间依赖范围未超出研究尺度，即调查间隔距离均在其变程范围内，具有明显的空间相关或依赖性。空间结构比0/（0+）在0.04%—69.77%，田块7和9分别为69.77%和32.42%（均处于25%—75%），属于中等程度的空间相关；其余田块均小于25%，属于强烈空间相关。田块2、8和10的决定系数2为0，但综合考虑半方差函数模型及其主要参数，确定其空间格局为聚集型；其余田块的2均大于0，表明理论模型与半方差函数曲线拟合程度较高，空间分布型为聚集型。

由Kriging插值获得的三维和二维空间插值分布图（图1）可知，桃蛀螟幼虫种群在玉米田中的聚集中心主要分布在田块边缘。其中，田块1和9的幼虫主要在玉米田的西北和西南部聚集（图1-A和1-I）；田块3、4和6的幼虫主要聚集在田块的西北位置（图1-C、1-D和1-F）；田块2和8的桃蛀螟幼虫主要在田地的东面聚集，西面次之，中间最少（图1-B和1-H）；田块5的幼虫主要在玉米田的中心地带和东北部聚集（图1-E）；田块7的幼虫种群数量由北到南呈阶梯状递减，且东北部聚集度最大（图1-G）；田块10的幼虫种群主要聚集在玉米田的东北部，中部数量最少（图1-J）。

表2 桃蛀螟幼虫种群的半方差函数模型参数及空间格局

2.3 基于Iwao回归模型的抽样技术

2.3.1 理论抽样数的确定 将Iwao回归方程的和值，代入理论抽样数模型公式得=(/)2(4.251/+0.041)。设=2，=0.1、0.2、0.3，求得桃蛀螟幼虫在不同平均密度情况下的抽样数（表3）。在相同允许误差情况下，随着桃蛀螟幼虫种群密度的增大，所需抽样数依次减少；在相同密度下，允许误差越大，所需抽样数越少。

m：距离，米Distance, meter

图1 桃蛀螟幼虫种群的三维和二维空间分布图

Fig. 1 The three-dimensional and two-dimensional maps oflarvae populations

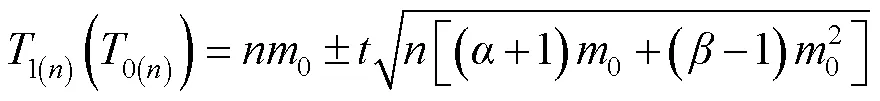
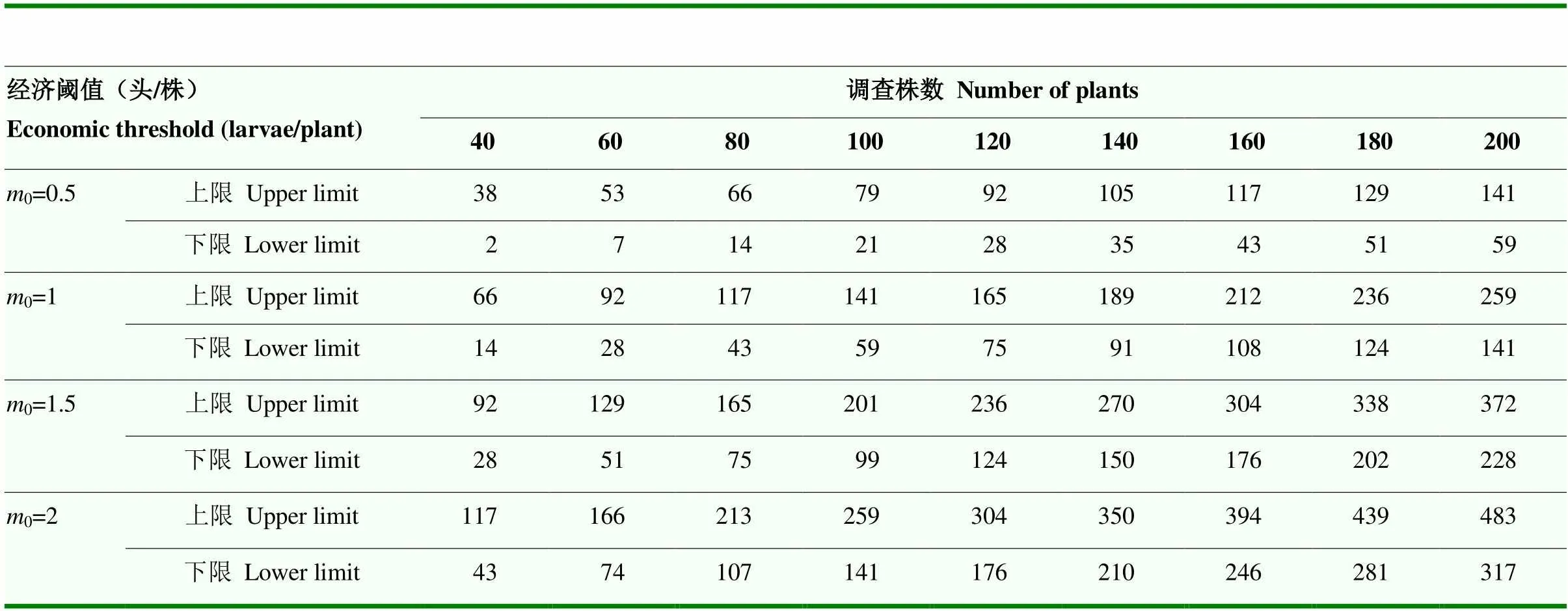
表4 桃蛀螟幼虫的序贯抽样表

3 讨论

3.1 确定昆虫空间分布型的理想途径

传统统计学方法（例如聚集度指标）可以定性了解昆虫种群的一些空间分布信息，但忽略了研究对象聚集的空间位置和相关程度，其结果很大程度上依赖于昆虫种群密度和所取样方的大小，无法反映其局部变化特征[3]，也无法用图示呈现昆虫在田间具体位置的真实分布特征与种群密度高低的变化。相比传统统计学方法随机选取样本的理论体系，地统计学方法以区域化变量理论为基础，兼顾样本值大小和空间方位及其相互距离的关系，定量描述昆虫种群的空间相关性和依赖性，且通过进行Kriging插值模拟，能用二维或三维图示直观地反映昆虫在田间的实际分布情况，包括种群的密度变化和聚集斑块的大小和方向[27-28]，从而弥补了传统统计学方法的不足，从根本上改变了传统统计学随机选取样本为基础的理论体系[27]。但地统计学不能对不同空间分布型给出具体的聚集度指标大小和分布型的具体形式，此时需要借助传统统计学方法测定的数据为地统计学分析提供支持，而且地统计学也不能提供田间抽样的信息。由此可见，仅依靠单一的统计学方法研究物种种群的空间分布型均存在一定的局限性，只有将传统统计学与地统计学方法结合起来，将两者综合运用才能更全面而准确地了解昆虫种群的空间分布特征。因此，本文结合两种统计学方法更准确地确定桃蛀螟幼虫种群的空间分布型类型，这对于桃蛀螟幼虫抽样计划的制定、预测预报与科学防治具有重要理论和实践意义。

3.2 玉米田桃蛀螟幼虫空间分布型的动态性及对田间抽样方法确定的指导作用

本研究利用多种聚集度指标法分析表明，桃蛀螟幼虫种群在玉米田的空间分布型属于聚集分布，且为一般的负二项分布，与吴立民[15]利用聚集度指标法的结果是聚集分布中的核心分布不同，产生不同的原因可能与抽样样方设置有关。该研究与郝立武[18]在同一块田大部分时间（在8月下旬至9月中旬）桃蛀螟幼虫种群呈聚集分布的结果相似；而王其武[19]研究发现，桃蛀螟种群在9月中旬之前属于随机分布，之后属于聚集分布，与本研究结果略有差异。本研究调查的玉米田块与郝立武[18]调查的玉米田周围林地和桃园较多，桃蛀螟发生量相对较大，成虫迁入玉米田的量自然就大，幼虫发生量较高、聚集度大。而王其武[19]调查的无棣县玉米田周围均为玉米环境，桃蛀螟发生量相对低，9月中旬之前成虫迁入量和幼虫发生量偏低，有可能形成随机分布。总的来看，桃蛀螟分布型的变化可能与桃蛀螟成虫从其他环境的迁入量、玉米田周围环境的复杂度（玉米田周围是否有果树如桃树等）、成虫迁入期与玉米的关键生育期（特别是抽雄吐丝至灌浆期）的吻合度有关。本研究采用在桃蛀螟发生盛期（灌浆期到乳熟期）的多块玉米田进行调查来明确其幼虫的空间分布型，具有很好的代表性，因此无论是从地统计学的模型数据还是二维与三维图示来看，结论完全与传统统计学方法相同，得到了相互印证，也体现了地统计学在研究空间格局上的优势。从地统计学的二维与三维图示看，桃蛀螟幼虫主要集中在地块边缘，这样在调查桃蛀螟幼虫种群数量时，为减少人为因素造成误差，建议采用“Z”字形取样法，以提高抽样结果的准确性，一般地，呈负二项分布的昆虫多建议用“Z”字形取样法[3]。鉴于在玉米穗期用多种抽样方法进行抽样准确性的比较需要剥开大量雌穗，而且易招引更多的桃蛀螟和亚洲玉米螟（）来产卵和危害而造成损失，本研究未做这方面的工作。

3.3 桃蛀螟幼虫抽样技术对制定桃蛀螟科学防治决策的指导意义

基于Iwao回归模型的抽样技术，其最大特点是不受调查对象分布型的限制。本研究依据Iwao回归模型提出了桃蛀螟经济阈值为较低幼虫密度（即经济阈值0为0.5、1、1.5、2头/株时）情况下的序贯抽样表，确定了最大理论抽样数。近期，王荣成[29]在山东泰安夏玉米田通过人工接虫的方法，结合产量损失和玉米价格等制定了防治桃蛀螟的经济阈值为1头幼虫/穗或1.1粒有效卵/株。因此，在进行桃蛀螟幼虫种群数量调查指导防治时，可应用本研究确定的序贯抽样表和最大理论抽样数。吴立民[15]基于Kuno序贯抽样模型[30]，提出了相应序贯抽样表，在虫口密度较高的情况下，允许误差（）取0.15，虫口密度较低的情况下，允许误差取0.25，一般情况下取0.2。本研究结合多年来对玉米田桃蛀螟的调查和该害虫的钻蛀危害习性，建议从有效卵到幼虫孵化期间（尚未钻蛀玉米时）作为防治的关键时期。倘若高龄幼虫钻入玉米雌穗内，防治难以奏效，很容易造成严重的经济损失。因此，明确玉米田桃蛀螟幼虫的空间分布型与适宜的田间抽样方法和抽样数，对于及时有效地控制桃蛀螟危害以确保玉米的安全生产具有重要意义。

4 结论

两种统计学方法分析表明，桃蛀螟幼虫在泰安市夏玉米田的空间分布型为聚集分布。传统统计学方法证明桃蛀螟幼虫种群为聚集分布中的负二项分布，且聚集强度随种群密度的升高而增加；地统计学方法确定了桃蛀螟幼虫种群的最优拟合模型为球型、指数型和线型，均为聚集分布，且聚集中心主要分布在田块边缘。基于Iwao回归模型明确的桃蛀螟幼虫理论抽样数和序贯抽样表能为其种群数量的准确估计和科学防治提供重要依据。

[1] 王振营, 王晓鸣, 石洁. 中国农作物病虫害: 上册. 3版. 北京: 中国农业出版社, 2015: 705-712.

WANG Z Y, WANG X M, SHI J. Crop Diseases and Insect Pests in China: part Ⅰ. 3rd ed. Beijing: China Agriculture Press, 2015: 705-712. (in Chinese)

[2] DU Y L, LI J, WANG Z Y. Research progress of(Lepidoptera: Crambidae) in China//CHAKRAVARTHY A K. The Black Spotted, Yellow Borer,Guenée and Allied Species. Berlin: Springer, 2018: 45-66.

[3] 丁岩钦. 昆虫数学生态学. 北京: 科学出版社, 1994: 22-69, 256-270.

DING Y Q. Insect mathematical ecology. Beijing: Science Press, 1994: 22-69, 256-270. (in Chinese)

[4] SCHOWALTER T D. Insect ecology: an ecosystem approach. 4th ed. London: Academic Press, 2016: 141-175.

[5] GARCIÁ F J M. Analysis of the spatio-temporal distribution ofHb. in a tomato field using a stochastic approach. Biosystems Engineering, 2006, 93(3): 253-259.

[6] GOZÉ E, NIBOUCHE S, DEGUINE J P. Spatial and probability distribution of(Hübner) (Lepidoptera: Noctuidae) in cotton: systematic sampling, exact confidence intervals and sequential test. Environmental Entomology, 2003, 32(5): 1203-1210.

[7] 周海波, 陈林, 陈巨莲, 程登发, 刘勇, 孙京瑞. 基于GIS的小麦-豌豆间作对麦长管蚜种群空间格局的影响. 中国农业科学, 2009, 42(11): 3904-3913.

ZHOU H B, CHEN L, CHEN J L, CHENG D F, LIU Y, SUN J R. Effect of intercropping between wheat and pea on spatial distribution ofbased on GIS. Scientia Agricultura Sinica, 2009, 42(11): 3904-3913. (in Chinese)

[8] 闫香慧, 赵志模, 刘怀, 肖晓华, 谢雪梅, 程登发. 白背飞虱若虫空间格局的地统计学分析. 中国农业科学, 2010, 43(3): 497-506.

YAN X H, ZHAO Z M, LIU H, XIAO X H, XIE X M, CHENG D F. Geostatistical analysis on spatial distribution of white-backed planthopper nymphs. Scientia Agricultura Sinica, 2010, 43(3): 497-506. (in Chinese)

[9] 高丙涛, 任利利, 蒋琦, 刘漪舟, 俞琳锋, 骆有庆. 不同受害油松林内红脂大小蠹空间格局的地统计学研究. 应用昆虫学报, 2020, 57(6): 1427-1435.

GAO B T, REN L L, JIANG Q, LIU Y Z, YU L F, LUO Y Q. Geostatistical analysis of the spatial distribution ofinforests with different levels of infestation. Chinese Journal of Applied Entomology, 2020, 57(6): 1427-1435. (in Chinese)

[10] PARK Y L, OBRYCKI J J. Spatio-temporal distribution of corn leaf aphids (Homoptera: Aphididae) and lady beetles (Coleoptera: Coccinellidae) in Iowa cornfields. Biological Control, 2004, 31(2): 210-217.

[11] 赵静, 赵鑫, 王玉军, 李光强, 刘丽平, 孟家华, 郑方强. 烟盲蝽及其天敌蜘蛛空间格局的地统计学分析. 生态学报, 2010, 30(15): 4196-4205.

ZHAO J, ZHAO X, WANG Y J, LI G Q, LIU L P, MENG J H, ZHENG F Q. Geostatistical analysis of spatial patterns of(Reuter) (Hemiptera: Miridae) and its natural enemy spiders. Acta Ecologica Sinica, 2010, 30(15): 4196-4205. (in Chinese)

[12] 洪波, 张云慧, 李超, 吐尔逊, 陈林, 程登发. 马铃薯甲虫空间分布型及序贯抽样. 植物保护学报, 2010, 37(3): 206-210.

HONG B, ZHANG Y H, LI C, TU E X, CHEN L, CHENG D F. Spatial distribution pattern and sequential sampling of Colorado potato beetle,Say. Journal of Plant Protection, 2010, 37(3): 206-210. (in Chinese)

[13] 孙小旭, 赵胜园, 靳明辉, 赵慧媛, 李国平, 张浩文, 姜玉英, 杨现明, 吴孔明. 玉米田草地贪夜蛾幼虫的空间分布型与抽样技术. 植物保护, 2019, 45(2): 13-18.

SUN X X, ZHAO S Y, JIN M H, ZHAO H Y, LI G P, ZHANG H W, JIANG Y Y, YANG X M, WU K M. Larval spatial distribution pattern and sampling technique of the fall army wormin maize fields. Plant Protection, 2019, 45(2): 13-18. (in Chinese)

[14] 杨紫涵, 何沐阳, 李建芳, 张富春, 王磊, 陆永跃. 草地贪夜蛾幼虫在苗期玉米田的空间分布格局及其抽样技术. 环境昆虫学报, 2020, 42(4): 817-828.

YANG Z H, HE M Y, LI J F, ZHANG F C, WANG L, LU Y Y. Spatial pattern oflarvae at seedling corn field and its sampling method. Journal of Environmental Entomology, 2020, 42(4): 817-828. (in Chinese)

[15] 吴立民. 玉米田桃蛀螟分布型及抽样技术. 江苏农业科学, 1995(3): 33-35, 53.

WU L M. Spatial distribution pattern and sampling technique ofin the corn fields. Jiangsu Agricultural Sciences, 1995(3): 33-35, 53. (in Chinese)

[16] 周洪旭, 乔晓明, 孙立宁, 顾颂东, 郑伯平, 赵春生. 玉米田桃蛀螟越冬幼虫空间分布型的研究. 山东农业大学学报 (自然科学版), 2004, 35(4): 543-546.

ZHOU H X, QIAO X M, SUN L N, GU S D, ZHENG B P, ZHAO C S. Studies on the spatial distribution pattern of overwintering larvae ofGuenée in the corn field. Journal of Shandong Agricultural University (Natural Science Edition), 2004, 35(4): 543-546. (in Chinese)

[17] 陈炳旭, 董易之, 陆恒. 桃蛀螟幼虫在板栗上的空间分布型研究. 环境昆虫学报, 2008, 30(4): 301-304.

CHEN B X, DONG Y Z, LU H. Studies on the spatial distribution pattern oflarvae in chestnut trees. Journal of Environmental Entomology, 2008, 30(4): 301-304. (in Chinese)

[18] 郝立武. 山东省夏玉米主要害虫种群发生动态及基于GIS和GS的空间分析[D]. 泰安: 山东农业大学, 2012.

HAO L W. The population dynamics of the main insect pests on summer corn field and their spatial analyses based on GIS and GS in Shandong province[D]. Taian: Shandong Agricultural University, 2012. (in Chinese)

[19] 王其武. 无棣县玉米田桃蛀螟幼虫时空动态和抽样技术研究[D]. 泰安: 山东农业大学, 2016.

WANG Q W. The temporal-spatial dynamics and sampling techniques of yellow peach borer larvae population on corn in Wudi county[D]. Taian: Shandong Agricultural University, 2016. (in Chinese)

[20] 唐启义. DPS数据处理系统——实验设计、统计分析及数据挖掘. 2版. 北京: 科学出版社, 2010: 489-491.

TANG Q Y. DPS Data processing system——experimental design, statistical analysis and date mining. 2nd ed. Beijing: Science Press, 2010: 489-491. (in Chinese)

[21] TAYLOR L R. Aggregation, variance and the mean. Nature, 1961, 189: 732-735.

[22] TAYLOR L R. Aggregation, migration and population mechanics. Nature, 1977, 265: 415-421.

[23] IWAO S. Application of*-method to the analysis of spatial patterns by changing the quadrat size. Researches on Population Ecology, 1972, 14(1): 97-128.

[24] IWAO S. The*-statistics as a comprehensive method for analyzing spatial patterns of biological populations and its application to sampling technique problems//MORISITA M. Studies on methods of estimating population density, biomass and productivity in terrestrial animals. Japanese Committee for the International Biological Program. Tokyo: University of Tokyo Press, 1977: 21-46.

[25] LIEBHOLD A M, ROSSI R E, KEMP W P. Geostatistics and geographic information systems in applied insect ecology. Annual Review of Entomology, 1993, 38: 303-327.

[26] IWAO S. A new method of sequential sampling to classify populations relative to a critical density. Researches on Population Ecology, 1975, 16(2): 281-288.

[27] 周国法, 徐汝梅. 生物地理统计学: 生物种群时空分析的方法及其应用. 北京: 科学出版社, 1998: 22, 47-48.

ZHOU G F, XU R M. Biogeostatistics: methodology and application of spatial analysis of biology species. Beijing: Science Press, 1998: 22, 47-48. (in Chinese)

[28] ROSSI R E, MULLA D J, JOURNEL A G, FRANZ E H. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecological Monographs, 1992, 62(2): 277-314.

[29] 王荣成. 桃蛀螟为害夏玉米的损失估计与经济阈值研究[D]. 泰安: 山东农业大学, 2020.

WANG R C. Research on loss estimation and economic threshold of the yellow peach moth,, on summer maize[D]. Taian: Shandong Agricultural University, 2020. (in Chinese)

[30] KUNO E. Some notes on population estimation by sequential sampling. Researches on Population Ecology, 1972, 14(1): 58-73.

Spatial Distribution Pattern and Sampling Technique ofLarvae in Maize Fields

College of Plant Protection, Shandong Agricultural University, Taian 271018, Shandong

【Objective】The yellow peach moth,, as an agricultural insect pest, its damage to maize ears has become more and more serious in Huang-Huai-Hai maize-producing areas of China in recent years, threatening the safe production of maize and the food safety. The spatial distribution pattern is an important ecological attribute of insect population, the objective of this study is to research the spatial distribution pattern oflarvae in maize fields, clarify the spatial distribution characteristics of the pest, and to provide scientific bases for formulating field sampling program oflarvae in maize fields, forecasting and effective management of the insect pest on maize.【Method】The spatial distribution pattern of the population oflarvae in maize fields was studied by traditional statistical method (aggregation indexes, Taylor’s power law and Iwao’s regression model) and geostatistical method. Based on the Iwao’s regression model, the theoretical sampling number oflarvae in fields was determined, and the maximum theoretical sampling number with different admissible errors (=0.1, 0.2, 0.3) and the putative economic thresholds (0=0.5, 1, 1.5, 2 larvae per plant) was also determined by the sequential sampling.【Result】The results of the two kinds of statistical methods showed that the spatial distribution pattern oflarvae belonged to aggregation distribution. The analysis of some aggregation indexes showed that spatial distribution pattern oflarvae belonged to aggregation distribution. The results of Taylor’s power law showed that the spatial distribution pattern oflarvae belonged to aggregation distribution, and the aggregation intensity increased with the population density. The Iwao’s regression model proved that the spatial distribution pattern oflarvae belonged to negative binomial distribution in aggregation distributions. The parameters of semivariogram models indicated that the optimal fitting models oflarvaewere the spherical, exponential and linear models. The three-dimensional and two-dimensional maps from Kriging interpolations showed that the aggregation centers oflarvae were located at the edges of the fields. Based on sampling technique from the Iwao’s regression model, the theoretical sampling number oflarvae in maize fields was determined when the confidence probability=2 and different mean densities=0.5, 1, 2, 3, 4, 5, 10 and 15. The maximum theoretical sampling number was also determined by the sequential sampling. Assuming=2,=0.1, 0.2, 0.3, when0=0.5 larva per plant, the maximum theoretical sampling numbers were 3 417, 854 and 380, respectively; when0=1 larva per plant, the maximum theoretical sampling numbers were 1 717, 429 and 191, respectively; when0=1.5 larvae per plant, the maximum theoretical sampling numbers were 1 150, 287 and 128, respectively; when0=2 larvae per plant, the maximum theoretical sampling numbers were 867, 217 and 96, respectively.【Conclusion】The spatial distribution pattern oflarvae belongs to the negative binomial distribution in aggregation distributions, and the aggregation centers were located at the edges of the fields. The maximum theoretical sampling number based on the sequential sampling in maize fields can be used for monitoring and management oflarvae.

; aggregation indices; geostatistics; spatial distribution pattern; sampling technique

2021-09-10；

2021-10-22

国家重点研发计划（2016YFD0300701）、山东现代农业产业技术体系（SDAIT-02-10）

李少华，E-mail：18763822737@163.com。通信作者李向东，E-mail：xdongli@sdau.edu.cn。通信作者郑方强，E-mail：fqzheng@sdau.edu.cn

10.3864/j.issn.0578-1752.2022.10.007

（责任编辑 岳梅）