银纳米线波导在量子光学中的应用（特邀）

吴赟琨，任希锋

（1 中国科学技术大学中科院量子信息重点实验室，合肥 230026）

（2 中国科学技术大学量子信息与量子物理协同创新中心，合肥 230026）

0 引言

表面等离激元（Surface Plasmon Polariton，SPP）是金属与介质界面上自由电子集体震荡所产生的电磁场［1］，具有能够突破光学衍射极限，将能量限制在亚波长尺寸区域的特点。这一独特性质由TAKAHARA J等于1997 年发现［2］，提供了一种精密操控光场、发展超紧密集成光学回路等应用的新途径。二十年多年来，表面等离激元得到了广泛研究和高速发展，在纳米光子激光器和放大器［3-4］、纳米光学天线［5］、生物化学传感［6］、超紧凑的集成光学回路［7］、突破衍射极限的光刻［8］等经典光学技术中都已得到了广泛应用。与此同时，光学领域另一革命性的突破——量子光学自诞生以来蓬勃发展，也激励着科研人员对表面等离激元进行量子层面的探索和研究。20 世纪50 年代已经发展出对金属中SPP 进行量子化的理论描述方法［9-12］，该描述将SPP 作为一种“准粒子”来看待，其很多量子性质也在后续工作中得到了研究和证明［13-14］，这使得人们对构建在量子水平上运行的表面等离激元纳米装置越发感到兴奋，并由此发展出将表面等离激元和量子光学相结合的新兴研究方向——量子表面等离激元［15-16］。特别是近年来微纳加工技术的提高，多种实验测量手段和强大电磁模拟方法的出现，更为该领域的发展提供了条件。

多种纳米结构都可以有效地传输局域量子表面等离激元，如纳米颗粒［17］、纳米孔洞［18-19］、槽状和脊状波导［20-21］、纳米天线［22-23］等等，其中一维波导结构能够在保持对光场高束缚性的同时，对光场的传播方向进行更好的引导和控制，因此在很多工作中被采用。金属纳米线是最常用和最有代表性的一维等离激元波导之一，常见材料包括金、银、铜、铝等。与其他金属材料相比，银具有最佳的导电和导热性能，是电互联的理想材料［24］。同时，金属银在300～1 200 nm 的光谱范围内都能支持良好的强共振，因此拥有从近紫外到近红外的超宽应用带宽［25］。具体到银纳米线这一结构，也在实际应用中有很多得天独厚的优势，比如良好的单晶结构、相对较低的传输损耗、成熟的制备工艺等等［26］。银纳米线上支持多种SPP 模式，这些模式具有各不相同的光学特性，因此选择性激发和控制银纳米线上特定的SPP 模式能够实现不同的功能［27］。进一步地，将银纳米线放置于不同的基底上，或对多根银纳米线进行级联和叠放，能够产生束缚更为紧密的gap-SPP 模式，对光场有更为强烈的局域增强效应［28］。由于银纳米线上SPP 的超高模式密度，利用银纳米线与单发光点进行耦合能够显著增强二者间的相互作用，从而有效调控单发光点的发射性质。而单个SPP 在银纳米线上的紧束缚传输，又使得利用银纳米线搭建超紧凑集成量子表面等离激元回路成为可能，一系列相关研究工作都已卓有成效［29］。

本文主要介绍银纳米线在量子光学和量子信息技术研究方向上的相关工作。首先对SPP 自身和银纳米线上SPP 的性质进行介绍，包括光学性质和量子性质，这些基本特性是银纳米线在量子光学领域得到应用的基础；然后介绍银纳米线应用在量子光学和量子信息的主要研究方向，展示和介绍其中代表性和最新的相关工作，包括与发光点进行相互作用，搭建量子集成表面等离激元回路和量子精密测量等；最后对目前银纳米线应用于量子光学工作中所面临的挑战和困难进行总结，并简要展望可能的解决方法和未来潜在的发展方向。

1 表面等离激元简介

近年来传统硅基电子回路的发展道路遭遇了瓶颈，一系列由于集成度提高随之而来的散热、能耗和延迟等问题难以解决，且逐渐逼近其带宽和信息传输速率的理论阈值。光子体系在这些方面表现出极大的天然优势：光子能够以光速进行传播，并且光脉冲的宽度可低于飞秒量级，因此相比于电子体系能够带来带宽和响应速度上数量级的提升。然而，虽然光子具有上述以及多自由度、良好的相干性质、较低的损耗等众多优点，但同时光子体系也存在两个最为关键和突出的缺陷，即相对较弱的光与物质相互作用和难以避免的光学衍射极限限制。光子和电子这些自身的固有缺陷极大地限制了其进一步发展，幸运的是，SPP 在很多方面继承了二者的优点，并且可能同时规避它们的很多缺陷。SPP 在保持光子传输速率和带宽的同时，能够突破光学衍射极限和显著增强光与物质相互作用，是一种极有潜力的信息载体，在信息处理中有着极大的应用前景。

首先从经典电磁场理论出发，介绍表面等离激元的基本性质。由于表面等离激元是金属与介质界面上集体震荡的自由电子形成的电磁场，将垂直于交界面的方向定义为y，光场传播平面定义为xy平面，并假设y＞0 部分为介质（对应介电系数ε1），y＜0 部分为金属（对应介电系数ε2），则只有在y方向有电场分量的横磁模（Transverse Magnetic，TM）能够对界面上的表面等离激元进行有效激发［30］。对于一个TM 电磁波，其电场和磁场可分别表示为

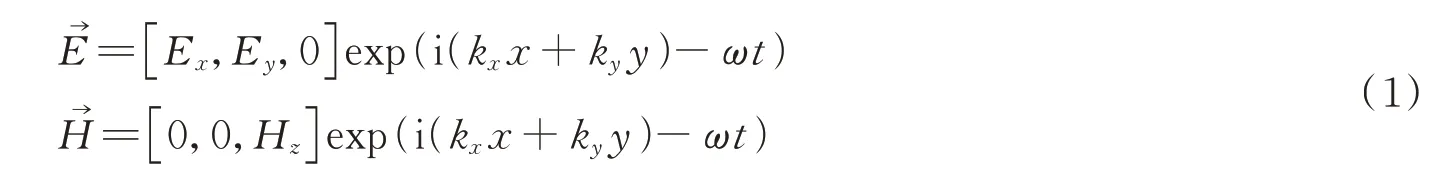
在无源场中，由麦克斯韦方程可得

因此可将磁场强度用电场分量进行表示。进一步地，考虑在金属和介质的交界面，根据边界连续条件可得

其中下标1，2 表示在两种不同材料中的情况。同时由矢量分解关系有

联立式（1）～（4），可求解出在平坦界面上传播的表面等离激元的色散关系为

由此可以看出，SPP 与自由空间的光波之间存在明显的动量失配［31］，因此自由空间入射光无法直接激发SPP，通常需要借助光的折射、衍射或散射等方式进行动量补偿。

同样根据SPP 波矢表达式，SPP 在平行于界面方向的波矢kx为一复数，而在垂直于银纳米线方向的波矢kyj为一纯虚数。这表示SPP 在平行于界面的方向上以行波的形式一边震荡传输一边逐渐衰减，而在垂直于界面的方向上以倏逝波的形式迅速衰减，由此可以定义几个常用的SPP 特征长度。kx的实部决定了SPP的波长，也就是沿着界面传播时电场场强的震荡周期

式中，下标r 表示金属介电常数实部，可见λspp总是小于入射光波长，因此在超分辨的传感和探测中有极大的应用潜力。另一个重要的特征长度是SPP 的传播长度Lx，其定义为SPP 沿着界面传播到强度衰减为初始值1 e 时所经过的距离，由kx的虚部所决定

类似地，SPP 在垂直界面方向传输到强度衰减为初值1 e 所经过的距离定义为穿透深度Ly，由kyj所决定

式中，下标i 均表示取虚部，由此可见Ly在两个相反的方向都总小于入射光波长，再次证明了能量在垂直于界面的方向能够被有效束缚在亚波长尺度，并产生极大的局域增强效应。由此通过简要的理论推导，证明了表面等离激元突破光学衍射极限的能量局域。该独特的性质使得表面等离激元得以在包括微纳光学、集成光学和量子光学的众多领域中得到广泛而有效的应用，在关于银纳米线的众多研究中，该优势同样得到了充分的发挥和利用。

2 银纳米线上SPP 的性质

2.1 基本光学性质

银纳米线是一种具有对称性的准一维纳米结构，根据第1 节，其SPP 能量能够在银纳米线与周围介质交界处的亚波长区域内被局域和传输。由于相位失配，最常用的激发银纳米线上SPP 的方法是用物镜聚集在纳米线端点或其表面缺陷处，通过散射实现动量匹配，而聚焦在纳米线中间的平滑区域则难以激发SPP。这一过程反过来也成立，即纳米线上的SPP 只会在端点或表面缺陷处以光子形式散射到自由空间中［32］，因此为了减少传输过程中额外的散射损耗，银纳米线应尽量保证表面的光洁和平滑。目前银纳米线的生产工艺已经十分成熟，发展出了包括气相制备［33］、光刻［34-35］、熔拉［36］等在内的多种物理方法，以及以溶液反应为代表的化学方法［37-38］，能够制备出具有不同几何形貌和表面特征的银纳米线。

DITLBACHER H 等在2005 年利用扫描近场光学显微镜（Scanning Near-field Optical Microscrope，SNOM）技术，在实验中直接观测到了银纳米线上传输的SPP 光场分布，并证明了其周期（波长）约为一半激光波长［39］。同时他们发现单晶纳米线的传输效率和端面反射率与多晶相比更高，因此单晶银纳米线可以看做一种SPP 的F-P 腔。同时银纳米线上传输SPP 的模式体积随波长变化不敏感，因此在从可见光到近红外的超宽工作带宽中，银纳米线都能够将能量有效束缚在亚波长尺度内，并产生极大的局域增强效应。这些优良的光学性质是表面等离激元的固有性质，接下来将介绍银纳米线自身特定的几何结构和材料所带来的光学性质。

一根银纳米线上能够同时支持多种SPP 模式，单晶银纳米线的横截面近似为五边形，这里为了简化计算过程，将银纳米线端面设定为圆形代替。首先给出悬空银纳米线上最低阶的两种模式，分别是横磁模TM01（图1（a））和杂化模式HE11（图1（b）），其中TM01为银纳米线的基模，HE11为包含两个互相垂直简并模式的二阶模［40］。这两种模式显而易见具有很多迥然不同的性质，如不同的近场电磁场能量分布，从而进一步带来了不同的远场辐射特性；基模的有效折射率虚部高于二阶模，因此对应于一个相对更短的有效传输距离；二者的偏振、模式面积、SPP 波长等光学特性都互不相同。图1（c）展示了二者的有效模式面积随银纳米线半径的变化情况。有效模式面积定义为

图1 银纳米线上SPP 模式的基本光学性质Fig.1 The basic optical characters of SPP modes on AgNWs

该参数常被用于衡量能量的束缚程度。由此可见随着银纳米线半径的减小，二阶模HE11逐渐呈现出场模趋于发散的现象，证明其是一种准截止模式；而基模不存在截止半径，在任意半径的银纳米线上都能有效束缚能量，因此在利用银纳米线SPP 超小模式面积以得到高空间分辨率的应用中，需要选择基模进行激发［41-42］。另一方面，基模始终保持径向的偏振特性，而二阶模则能够保持激发光的线偏振性质，因此能够利用银纳米线的二阶模对偏振进行编码，从而携带信息甚至偏振纠缠态［43］。由此可见分析和控制纳米线上激发的SPP 模式具有重要的意义，近年来也有利用近场［44-47］、远场［27］等不同技术的相关工作报道，为银纳米线的进一步研究和应用铺平了道路。

在更多的实验中，银纳米线被置于各种不同的基底之上，图1（d）、（e）分别给出了银纳米线放在硅衬底和间隔10 nm 放在银衬底上的模式分布。可以明显观察到，衬底的存在使得SPP 的能量分布更集中于纳米线与衬底之间的间隙区域，尤其是当银纳米线置于像银这种金属基底上时，能够产生更为紧凑的gap-SPP模式［46］，同时间隙中的电场强度得到强烈的增益，类似的现象也发生在两根靠得很近的相邻平行银纳米线中间。由此可见，银纳米线被放置于衬底上，或模式体积内存在其他结构时，其SPP 模式会受到强烈的调制，包括模式分布在内的很多性质都会发生改变［48］。因此在实际应用中银纳米线与周围环境间的耦合作用影响不可忽略，但这也反过来给了银纳米线用于某些要求更高态密度应用的更多可能性。

虽然本征模TM01和HE11沿银纳米线传播时的电场振幅都是横向对称且均匀分布的（图2（a）、（b）），但当这两种模式同时在银纳米线上被激发时，二者会发生干涉和干扰，并且由于它们具有的横向对称性并不相同，因此会形成不对称的之字形电场分布，如图2（c）。同时该之字形电场分布呈现出明显的周期性，这是由于SPP 的拍频效应所造成的。基模与二阶模的有效折射率有一定差异，因而在传播一段距离后会分别累计不同的相位，导致电场的最大值在传播方向上周期性出现。该周期可由Λ=λ(nTM-nHE)计算得到［49］。考虑到这两种模式的有效折射率都对银纳米线半径存在依赖关系，更细的银纳米线上将对应更短的之字形周期。

图2 银纳米线上SPP 模式的传输性质Fig.2 The propagating properties of SPP modes on AgNWs

而当二阶模HE11的两个简并模式之间相差π 2 相位，并在同一根银纳米线上进行叠加时，则会形成一个具有螺旋相位分布的态，这种螺旋模式再与基模TM01进行干涉，能够进一步产生一个沿银纳米线表面螺旋分布的近场能流，如图2（d）。该现象在文献［50］中通过利用量子点覆盖银纳米线，在不同线偏振光激发银纳米线上的SPP 时，观察分析量子点的荧光强度图而间接证明。进一步地，当银纳米线置于基底上时，采用不同的圆偏振光直接激发SPP 能够指向不同的空间路径［51-52］。这种自旋相关的定向激发是由于光的自旋-轨道角动量耦合（Spin-orbit Interaction，SOI）所导致的［53-54］，当圆偏振光在均匀介质中沿着弯曲的轨道运动时，光子的自旋角动量耦合至其轨道角动量，而假设总角动量需要保持守恒，从而自旋相关的空间偏差随之产生。光子的这种SOI 效应在介质中一般非常微弱，但在SPP 存在的金属和介质界面处，由于较大的介电常数梯度，使得该效应发挥着不可忽视的作用。这些手性和自旋依赖的SPP 在银纳米线上传播的性质，在近年吸引了广泛的兴趣和研究，可进一步用于实现可控的传播方向调制和信息编码等应用中。

2.2 量子性质

虽然20 世纪50 年代已经发展出对表面等离激元进行量子化的理论描述方法［55-56］，但由于当时实验和模拟技术的限制，直到2002 年才首次报导了对SPP 量子性质的实验研究工作［57］。在该工作中双光子偏振纠缠态经历了先转化为SPP，然后再次转化为光子辐射到自由空间被探测的过程，并对最终得到的光学态进行了量子测量和分析。实验结果证明，在这整个过程中，量子态的纠缠性质一直得到了良好的保持。此后其他的量子纠缠态，如时间-能量纠缠［58］、轨道角动量纠缠［59］、连续变量量子态［60］等也都被转为SPP 后再次以光子形式被探测，证明了SPP 能够实现良好的量子纠缠性质，从而在量子集成回路中得到应用。接下来详细介绍利用银纳米线上SPP 来产生或传输量子纠缠态的代表性工作。

量子力学的基本特性之一是单个量子激子能够同时表现出波和粒子的性质，也就是波粒二象性。其中波动性主要体现在能够根据相位进行各种干涉作用，而粒子性则主要体现在其统计分布的规律上。最早同时证明SPP 具有波粒二象性的实验就是在银纳米线上完成［61］，由KOLESOV R 等利用单个氮空位（Nitrogen-Vacancy，NV）色心激发银纳米线上的SPP，再传输至银纳米线两个端点后，再次转化为光子形式辐射到自由空间进行测量。实验示意如图3（a），因此在这个过程中银纳米线也同时充当了分束器（Beam Splitter，BS）的功能，使得被激发的SPP 沿前后两个传输方向被分开，从而可以直接对从两端口出射的光子进行二阶关联函数测量，如图3（b）。实验结果表现出典型的单粒子自相关二阶关联特性，证明了被激发的SPP 每次只能辐射一份能量，即被单NV 色心所激发的SPP 也是单个的，其粒子分布性质得到了证明。波动特性则通过SPP 的自干涉来证明，类比光波在马赫曾德干涉仪（Mach-Zehnder interferometer，MZ interferometer）中干涉的过程，被激发的SPP 向前和前后传播可以视为第一个BS，向后传输的SPP 在银纳米线后端面反射后与向前传输的SPP 在前端面汇合，前端面可以视为第二个BS，并在端面处具有不同光程的相干SPP 发生干涉（另一个方向亦然）。因此直接测量银纳米线端口的SPP 散射强度能够观察到明显的干涉条纹，如图3（c），SPP 的波动性由此得到了证明。

图3 银纳米线上SPP 波粒二象性的实验证明［61］Fig.3 Experimental demonstration on Wave-particle duality of single SPP on AgNWs［61］

KOLESOV R 等的工作关注在银纳米线上单个SPP 量子性质的研究，也仅涉及到SPP 的一阶干涉。而多光子之间的二阶强度干涉是光场量子化后其量子性质的重要体现方式，其中最具代表性的便是Hong-Ou-Mandel（HOM）干涉。全同光子对转化为SPP 再转化回光子后，其全同性质仍然得到保存，能够继续发生HOM 干涉的特性已经在2012 年得到验证［62］。但想要证明SPP 自身的量子性质，需要SPP 在SPP 波导中直接进行HOM 干涉。干涉可见度高于经典极限的双SPP 量子干涉已经在多个工作中被报道［63-65］，其中任希锋课题组获得了高达95.7%的SPP HOM 干涉可见度（如图4），充分证明了SPP 的玻色量子性质［65］。虽然为了减少损耗得到更高的干涉可见度，这一部分的工作都选择了介质加载的杂化SPP波导，而不是在银纳米线上完成，但银纳米线上的SPP 同样具备这一基本性质，这也是利用银纳米线搭建量子集成SPP 回路，并在其中实现各种量子门操作、制备SPP 纠缠态、进行量子隐形传态等一系列工作的基础。

图4 SPP 之间发生HOM 干涉的实验证明［65］Fig.4 Experimental demonstration on HOM interference between SPPs［65］

值得一提的是，虽然光子的众多量子性质在转化为SPP 的过程中都能够保持，但由于欧姆损耗和表面散射等各种损耗的存在，容易导致量子退相干，这一现象也已经在多个工作中被证实。目前也有一些关于SPP 损耗的研究，如MARTINO D 等发现SPP 传播过程中的损耗与不相关的马尔科夫线性损失模型一致［66］。除了线性损耗之外，量子SPP 中的色散效应也被FUJII G 等研究［67］，发现可能导致SPP 系统的时间和光谱模式失真，因此在银纳米线上量子SPP 的实验中也要考虑损耗对实际结果的影响。但反过来，利用这些损耗有时也能达到非常规的效果，如理论和实验上都证明了由于损耗而造成的SPP 反凝聚现象［68］，这意味对待SPP 系统的损耗仍需要更深入的研究和理解，从而进一步控制甚至利用损耗［69］。

3 银纳米线在量子光学中的应用

第2 节中从银纳米线自身材料和结构、SPP 光学性质和量子性质等多个方面列举了银纳米线在实际应用的优势。在经典光学中银纳米线已经被用于传统波导［70］、集成激光器［71］、柔性光电探测器［72］、表面增强拉曼散射（Surface Enhanced Raman Scattering，SERS）［73］等众多应用中，而基于上述的优势和特点，银纳米线在量子光学领域也有着极大的应用潜力和空间，本节将主要从银纳米线与发光点相互作用、搭建量子集成回路、用于量子精密测量三个方面介绍近年来相关的工作进展。

3.1 银纳米线与量子发光体相互作用

利用SPP 与发光体进行相互作用是一直以来的研究热点，银纳米线是其中最常用的SPP 结构之一，在弱耦合和强耦合范围都有应用和研究。随着研究的深入，近年来该方向的研究热点逐渐转向银纳米线对单个量子发光点（Single Photon Emitters，SPEs）进行调制作用，本文主要介绍这部分的相关工作。

3.1.1 Purcell 效应

确定性单光子源在量子信息和量子计算领域都是关键性元器件，衡量一个单光子源的品质主要有三个指标：单光子纯度、全同性和亮度。为了获得更佳性质的单光子源，包括原子、分子、量子点、色心在内的多种材料体系都得到了大量的研究和发展，其中提高其发光效率的重要研究手段之一，就是利用其它微纳结构与单光子源进行相互作用。

一般而言，单个量子发光点的发光为自发辐射过程，其自发辐射速率是该发光点的内秉属性。然而PURCELL E M 在1946 年开创性的工作中指出，量子发光点的自发辐射速率也能被周围环境所影响和调制，这个现象就是著名的Purcell 效应［74］，该调制因子也被称为Purcell 因子，并随后被DREXHAGE K H 的实验所证明［75］。在大部分工作中，Purcell 因子以腔量子电动力学和腔品质因子的形式给出，这里给出在一维SPP 波导结构下该过程简要的理论描述［76］。

根据费米黄金定律［77］，SPE 的自发辐射速率与该处的局域态密度（Local Density Of States，LDOS）成正比［78］

式中，Γ是光源的自发辐射速率，ω是跃迁频率，d是跃迁偶极矩大小，r0表示位置，μ̂为偶极子取向单位矢量，ρ为LDOS，其物理意义为单位频率和空间的光场数目，可通过并矢格林函数G(r，r，ω0)求得

而对一个传播轴为z轴的一维表面等离激元波导而言，其附近的并矢格林函数可近似写为

式中，υg为群速度，其值为

N为归一化因子，其值为

式中，积分下标A∞表示对整个横截面进行积分运算。于是将关于并矢格林函数的表达式代入LDOS 和衰减速率的表达式中，即可计算出一个单发射点自发辐射到该SPP 模式通道，与在真空态中自发辐射Γ0的速率之比为

式（15）给出了一个SPE 能量辐射到波导导模通道中的自发辐射速率表达式，总自发辐射速率应该再加上辐射到自由空间和非辐射通道的速率，该值可以通过求解全场的电流密度计算得到。但在很多应用中，表面等离激元波导的影响要远远超过另两个通道，因此该式可以用来近似作为Purcell 因子的表达式，并配合已经很成熟的各种数值计算方法，如有限元法和时域有限差分法等进行仿真计算。在实验中，Purcell 因子的测量通常通过SPE 的辐射寿命变化进行表征，同时能够观察到其发光强度的提高。

3.1.2 弱耦合

由于微纳结构与发光体之间的耦合强度正比于(1/Veff)12，其中Veff为微纳结构的有效模式体积［79］。因此具有较大模式体积的介质波导很难与SPE 进行较强的相互作用，强色散的光子晶体波导可以通过减慢光的群速度来对弱相互作用进行补偿，但较大的模式体积仍然使其难以对单个SPE 进行局域操控；高品质因子的光学纳米腔也能够有小模式体积，但又会带来信号能量难以提取的新挑战，且一般工作带宽较窄。幸运的是银纳米线在这些问题中都有着天然的优势，SPP 的小模式体积提供了更高的模式密度，从而能够实现更强的SPP-SPE 相互作用和突破衍射极限的局域控制，并且由于银纳米线的超宽工作带宽，这一局域增强效果并不受到窄共振线宽的约束。

在弱耦合范围内，银纳米线与SPE 进行相互作用一般是对发光体进行有效的调控，从而达到高效收集，或改善辐射性能的目的［80］。如3.1.1 节所述，由于银纳米线SPP 模式区域内超高的局域态密度，最常见的对SPE 的调控是改变其辐射速率和发光强度［81］。利用银纳米线对SPE 进行调控，观察到寿命大幅降低和发光强度得到显著增益的工作有很多。其中最早的代表性实验工作，由哈佛大学LUKIN M D 课题组于2007 年完成，首次实现了银纳米线与单量子点的耦合，并同时观察到了单量子点荧光2.5 倍的增强［82］。此后利用银纳米线对多种类型的SPE，如单量子点（Quantum Dot，QD）、二维材料单缺陷发光、NV 色心等进行耦合都已经在实验上实现［83-84］，并且调制特性扩展到辐射方向、偏振、模式等多个自由度［85］。在这类工作中，如何精准控制SPE 的位置，使其刚好位于银纳米线SPP 的超小模式体积内是实验的难点。最常用的方式一般有两类：利用纳米针尖或其他材料转移技术，事先将SPE 转移至银纳米线附近［84］，如图5 所示；另一种替代方法为在基底上随机散落大量SPEs 和银纳米线，然后再通过后续观测手段找到其相对位置满足要求的样品，最后进行测量［85］，如图6 所示。在该工作中单QD 的辐射模式因为银纳米线的对称结构分裂为两瓣，辐射方向与辐射偏振同时受到调控。

图5 银纳米线调制单个NV 色心辐射寿命［84］Fig.5 Modulating the lifetime of a single NV center with AgNWs［84］

图6 银纳米线调制单量子点辐射方向［85］Fig.6 Modulating the radiation direction of a single QD with AgNWs［85］

但是很显然这两种常见方式或者操作难度较大，或者成功概率较低。近年来逐渐发展出一些无需事先材料转移也能够确定性对SPE 进行调控的方法。TAO Cai 等报道了一种通过银纳米线带来的应变梯度，诱导覆盖的二维材料WSe2在银纳米线表面处自然产生SPE，从而实现SPE 与SPP 自对准而进行高效耦合的方案［83］，如图7。类似地，也可以利用化学方法实现SPE 与银纳米线的自组装，如将单个NV 色心自下而上自组装至银纳米线端面附近等［86］。将控制相对位置的途径从移动SPE 改为移动银纳米线［87］，任希锋课题组近期完成了利用光纤锥使银纳米线悬空作为一根可自由移动的探针对SPE 进行调控的工作，如图8 所示。从3.1.1 节中LDOS 和Purcell 因子的表达式，可以看出二者都强烈依赖于偶极矩的矢量方向，由此该工作进一步从实验和理论详细研究了这种悬空银纳米线调制方案对SPE 偏振的依赖关系，最终利用同一根探针对衬底上任意位置的单QD 实现了平均Purcell 因子为3.38 的寿命调控，以及对同一个氮化硼单缺陷发光实现寿命增加和减小的可控切换调制［88］。同时在这些银纳米线与SPE 高效耦合的工作中，为SPE 产生了一个新的辐射通道，即大量的SPE 能量耦合至银纳米线的SPP 模式中，因此银纳米线同时也可作为天线实现对SPE 辐射的高效收集。这种SPP 增强耦合的机制在电磁诱导透明、非反转激光等现象中也扮演了重要角色［89-90］。

图7 银纳米线与WSe2单缺陷点发光自对准耦合［83］Fig.7 The self-aligned coupling between SPEs in WSe2monolayer and AgNWs［83］

图8 银纳米线探针对基底上任意位置SPE 的偏振依赖寿命调制［88］Fig.8 The polarization-dependent lifetime modulations of arbitrary SPEs on substrate with an AgNW probe［88］

除了与单个SPE 进行耦合，一根银纳米线同时耦合两个甚至更多的SPE 的情形在实际实验中更为普遍，也对构建多SPE-SPP 杂化回路系统具有重要意义。BOUCHET D 等通过直接激发与银纳米线耦合的单个QD 发射单个SPP，并远程激发与银纳米线耦合的荧光分子，同时观察到了受体荧光分子与QD 表现出协同关联的闪烁行为，证明了二者的线性相关［91］，如图9 所示，也验证了早前对于耦合至同根银纳米线的多个SPE 之间的远程量子关联的理论［92］。武汉大学徐红星课题组同样在一根银纳米线上耦合了多个SPE，并通过调节银纳米线上的SPP 干涉场实现了对不同SPE 的局域激发，由于SPP 的波长小于衍射极限，该方法能够对多个SPE 进行超分辨的控制［93］，如图10。由此可见这种与多SPE 耦合的杂化SPP 波导结构不仅能够提高能量传输距离，实现对SPE 突破衍射极限的操纵，也提供了一种新的超分辨成像方法，并且开辟了研究超辐射等协同发射现象的新途径。另一方面，研究单个SPE 与多个表面等离激元电磁场的相互作用也极具研究价值。2020 年，SCHÖRNER C 和LIPPITZ M 在两根单晶银纳米线间隙中同时传输可见波段的泵浦SPP 和红移的耗尽SPP，并将单个甲苯二亚胺分子放置于gap-SPP 模式场内，同时与两种SPP 进行相互作用，从而观察到的荧光发生受激发射损耗（Stimulated Emission Depletion，STED）现象［94］，如图11。该工作证明了单分子与SPP 之间的远程非线性四波混频效应，并且效率比远程激励方式提高了五十倍，推动了功能性量子SPP 回路的发展。

图9 银纳米线上单量子点和单荧光分子的关联发射［91］Fig.9 The correlated emission between a single QD and a fluorescent nanobead on the same AgNW［91］

图10 一根银纳米线与多个单量子点进行耦合［93］Fig.10 The coupling between several single QDs and an AgNW［93］

图11 SPE 与银纳米线SPP 之间远程非线性四波混频［94］Fig.11 The remote nonlinear four-wave mixing between SPE and SPP on AgNWs［94］

3.1.3 强耦合

当光与SPP 之间的耦合强度继续增大，甚至耦合速率超过其衰减速率时，便进入到强耦合的相互作用机制［95］。此时能量在SPP 与光子之间来回相干振荡，因此SPP 的存在不能够仅仅看作是对光子的干扰或影响，而应该将二者看作一个整体系统看待，从而可以在实验上观察到能级的Rabi 劈裂［96-97］。强耦合这种独特的相互作用机制能带来迷人的物理和化学性质，因此在包括量子信息的许多领域都有应用，如量子霍尔效应、玻色-爱因斯坦凝聚、超流体、拉曼散射等等。SPP 也是探索强耦合现象的常用体系之一，从SPP 模式与系综发光体之间的强耦合相互作用［98］，到SPP 与单个发光体之间强耦合相互作用都逐一在实验上被实现［99-101］，且大部分是利用具有超高局域态密度的强局域gap-SPP 模式。

银纳米线与量子发光体在强耦合相互作用下的工作目前还相对较少，2018 年GARY B 等报道了在一个开放的单根银纳米线纳米腔中，实现了与菁染料（TDBC）激子之间强耦合的工作［102］。该工作中通过背向焦平面显微镜对银纳米线上SPP 的倏逝波进行观察和测量，并通过改变波长最终得到色散曲线。在银纳米线上沉积一层TDBC-PVA 薄膜后，测量到的色散曲线呈现出强耦合典型的反交叉现象，计算出的Rabi 分裂频率最大可达Ω=390±80 meV，如图12。此外一些诸如利用两根相对的、端面形状为锥形的银纳米线实现强耦合的仿真方案［103-104］，或是金属纳米线波导与两个三能级SPE 同时发生强耦合，从而使这两个SPE 之间实现量子纠缠的方案等理论相关研究也早有报道［105-106］，但其在银纳米线上的实验验证还仍待研究。

图12 单根银纳米线纳米腔与菁染料激子之间强耦合［102］Fig.12 Strong coupling between the TDBC exciton and AgNW nanocavity［102］

3.1.4 当前困难和可能发展

利用银纳米线实验实现SPP-SPE 强耦合目前仍然颇具挑战，主流的思路是采用具有更紧束缚能量的gap-SPP 模式。为了提高耦合强度，除了需要从理论上更加仔细地设计具有强Purcell 效应、高量子产率和合理传播长度的耦合结构之外，同时要求实验上银纳米线具有更精细的几何结构，可能通过对银纳米线进行进一步微纳加工，或探索具有特殊形貌银纳米线的制备工艺实现。在实验上，银纳米线与SPE 之间的相对位置也需要更为精准的纳米级控制，各种诸如原子力显微镜的近场工具和技术可以在其中得到应用。在弱耦合方面，除了实现更大的Purcell 因子、更灵活的调制手段、更高的收集效率等方向，也逐渐朝着与多个SPE 同时耦合的复杂杂化体系发展，可能需要首先对精准定位SPE，并独立实现每个SPE 可控激发的方式进行探索性研究。

3.2 银纳米线搭建量子集成回路

搭建量子集成回路是银纳米线在量子信息和量子光学中的另一重要应用，因为SPP 的亚波长局域和显著的电场增强效应，使得基于SPP 的量子回路可以不受光学衍射极限限制而缩小至纳米尺寸［107］。同时SPP之间的近场干涉，以及模式内增强的电磁场，对产生线性和非线性作用，实现更多样的光场操控提供了可能［108-110］。同时银纳米线是一种良好的SPP 波导，不管是与多根银纳米线进行进一步级联，还是与其他微纳结构形成杂化系统都有着天然的优势。对于一个完整的量子SPP 集成回路，应该包括量子SPP 的产生、态操作和测量三个部分，但由于目前工作中银纳米线几乎不会直接作为SPP 探测器工作，这里主要从前两个方面进行介绍。

3.2.1 量子SPP 产生

银纳米线上量子SPP 的产生，一般采用外部SPE 与银纳米线耦合的直接方法，或将制备好的量子态与银纳米线耦合的间接方法。对于产生单个SPP 而言，近年来的研究主流还是采用各种不同的SPE，如单个QD、二维材料单缺陷、NV 色心等等直接进行激发。在2.1.1 节Purcell 效应的介绍中已经指出，当SPE 置于银纳米线附近时，能够打开一个自发辐射至银纳米线SPP 模式的新通道，尤其是当二者之间的相互作用较强时，意味着SPE 的大量能量耦合至SPP 能量，从而实现了银纳米线上单个SPP 的有效激发。因此这部分工作与之前的银纳米线与单SPE 相互作用有很大重合［111-116］，由于前面已经做了详细介绍，这里仅给出几个代表性工作。图13（a）和图13（b）分别展示了单个QD 和单个NV 色心与银纳米线耦合，激发单个SPP 的实验示意图［117-118］，对SPP 的散射光进行二阶自关联函数的测量都能得到典型的单光子源HBT（Handury Brown-Twiss）图样。图14 展示了徐红星课题组同时将两个单QD 与同根银纳米线进行耦合，并通过超分辨成像和时间轨迹测量相结合的方式，分析了每个QD 独立激发产生单个SPP 的情况［119］。该工作与之前介绍的同课题组利用银纳米线超分辨局域激发单个QD 的工作相比，设计思路一脉相承，但实现方法和实验目的刚好相反。

图13 各种SPE 激发产生银纳米线上单SPP［117-118］Fig.13 Single SPP on AgNWs excited by different kinds of SPEs［117，118］

图14 多个QDs 独立激发产生银纳米线上单SPP［119］Fig.14 Resolving single SPP generated by a pair of quantum dots on an AgNW［119］

除了产生单个SPP 以外，在银纳米线上产生其他非经典态SPP 的常用方法，是将已经制备好的非经典光学态，如自发参量下转换产生的关联双光子、量子纠缠态等耦合至银纳米线进行激发。能够这样直接利用量子光学态对SPP 进行泵浦，实现量子光态至量子SPP 态的转换，得益于在第2 节中提到的SPP 能够对激发态的量子性质进行保持和传递的能力。同时由于前面介绍的波矢失配，远场激发一般要用物镜聚焦在银纳米线散射点［32］，或是利用光栅、棱镜等波矢补偿进行耦合，但这些传统的远场方式激发效率仍然较低［120-121］，低耦合效率和其他光学损耗会造成退相干和量子性质的丢失。近年来涌现了很多利用其它微纳结构与银纳米线形成杂化系统，从而进行近场耦合和高效激发SPP 的工作［122-123］，其中一种光纤锥耦合金属纳米线的杂化波导结构被多次报道。该结构能够将光纤中的光场模式进行绝热压缩，再通过近场耦合的方式，实现光纤锥中波导模式与金属纳米线上SPP 模式之间的高效相互转换［124-126］。这种光纤锥-银纳米线杂化波导结构天然满足光纤集成，是一种高效率激发银纳米线上SPP 的方式，除了在经典光学中被用于模式控制［27］、生物内窥镜［41，127］、高效率近场探针［128］等应用以外，最近在量子SPP 中也得到了研究。任希锋课题组利用该杂化结构，先后在银纳米线上激发了SPP 偏振纠缠态和量子NOON 态［43，129］，分别如图15（a）、（b）所示。这些量子SPP 态在银纳米线端点再次转化为光子辐射出来并被测量，测量结果显示在银纳米线上产生并传输超过10 μm 后，其量子态保真度仍然分别高达93.2%和87.9%。由于在这些工作中，SPP 量子纠缠态同时被束缚在亚波长尺寸，该结构在传输量子态，实现超分辨和超灵敏的精密测量和传感中有极大的应用潜力。

图15 银纳米线上SPP 纠缠态的产生［43，129］Fig.15 The entangled SPPs generated on AgNWs［43，129］

3.2.2 量子SPP 操控

如2.2 节所述，由于银纳米线上支持多个传播模式，在多模叠加的情况下SPP 在银纳米线上的传输表现出多种有趣的性质，包括之字形电场分布、拍频特性、手性和自旋依赖传播等等。这些性质可用于操控银纳米线上SPP 的电磁场，进而实现不同功能的光子器件。比如通过改变激发光偏振，调节合适的相位关系等，可以控制银纳米线上的模式分量和电场分布，从而提供了一种银纳米线网络中SPP 路由的方式。而由于基模和二阶模具有不同的横向对称性，因此通过引入结构对称破缺，能够实现银纳米线上的模式转换。常见的方式包括在银纳米线附近放置纳米颗粒破坏对称性，构建分叉或交叉的银纳米线网络，以及采用弯曲的银纳米线等等。基于这些性质和思路，在经典光学中银纳米线已经被应用于各种光学调控的SPP 回路元件［130-131］，如级联多根银纳米线，并在不同端口入射特定SPP，通过这些银纳米线与相邻纳米线SPP 之间的相干干涉，能够以多种方式组合信号，从而实现分路器、路由器、开关、多路复用器等多输入、多输出的SPP 集成回路器件［132］，如图16（a）。在此基础上，徐红星课题组通过精确设计利用多根银纳米线上SPP 的干涉，搭建了OR 和NOT 逻辑门，并更进一步级联实现了表面等离激元NOR 逻辑门［133］，如图16（b）。这种普适逻辑门操作是进行布尔逻辑运算的重要元素，对实现可扩展的复杂集成光学处理芯片有着重要意义。童利民课题组同样在利用金属纳米线搭建集成回路的研究方向上做了大量工作，不管是直接对纳米线自身形貌和结构进行微纳加工，使之成为功能性集成元件［134］，还是将金属纳米线与更为成熟的硅基光子芯片进行灵活、精准的集成化［123］，都对在银纳米线上利用SPP 实现多种光学调控提供了思路和参考。近年来随着微纳器件与矢量光场的结合，一系列关于银纳米线手性［135-136］，基于纳米线的轨道角动量选择转向器［137］、轨道角动量读出［138］等等功能性器件或内在物理性质得到了更深入的研究，使着银纳米线上的光场调控朝着矢量和复杂化的方向发展。同时由于这些银纳米线器件上能够传输和保持量子SPP 的相干性和其他性质，因此同样适用于搭建集成的量子SPP 光学网路，实现对SPP 态的线性操作。2.2 节中也已经介绍过SPP 的玻色性质能够实现量子HOM 干涉，以此为基础可以搭建量子C-NOT 等逻辑门操作，进一步丰富银纳米线上的集成化量子信息处理过程。

图16 利用级联银纳米线搭建集成功能性器件和量子逻辑门［132，133］Fig.16 The integrated functional devices and quantum logic gates realized with cascade of AgNWs［132，133］

银纳米线上SPP 之间的非线性作用，或SPP 与其他物质之间的非线性作用（如SPP-SPE 强耦合）同样能够实现量子态操作，且与线性操作相比，非线性能够提供更为高效的操控，是更为理想的实现途径。经典光学中已有不少利用银纳米线增强非线性的工作报道，如徐红星课题组在2017 年介绍了一种银纳米线-单层二硫化钼的杂化体系，利用远程激发的SPPs 在单根银纳米线中产生了轴向准直但横向发散的二次谐波SHG，为在亚波长波导中产生和操纵SHG 发射奠定了基础，同时为实现片上高效的非线性光学提供了新的可能［139］。但由于哪怕经过SPP 增益后的非线性作用一般仍然较弱，实验上在银纳米线上通过非线性直接实现复杂量子操作难度太大，目前基于该机制的量子操作研究大多还停留在理论层面，一些新方案被提出亟待验证和实现。LUKIN M D 课题组在早期曾经提出过利用SPE 与金属纳米线上传输SPP 之间的强耦合，将该系统作为一个非线性双光子开关的方案［140］。除此之外，该工作详细讨论了通过调节纳米线和SPE 的相互作用从而实现单光子晶体管功能的可能性，其中作为控制门‘gate’的单个光子存在与否，能够有效决定后续作为信号‘signal’的光子是继续沿纳米线传播或被阻断，如图17。中科大孙方稳课题组于近期最新报道了利用银纳米线-蝴蝶结天线结构对自由空间微波场进行收集、局域、和增强与电子自旋相互作用的工作［141］，如图18。实验上除了观察到8 个数量级的微波能量增强，和4 个数量级的相互作用提升之外，该工作同时证明了银纳米线-蝴蝶结结构能够用于高空间分辨率的量子比特操控。因为该结构具有偏振敏感性，使得通过自由空间微波场偏振的改变，对自选比特的选择性操控成为可能。由于SPP 与量子发光点之间实现较强非线性作用相对而言更容易实现，因此在介绍SPP 与SPE 进行耦合的部分工作也有应用于SPP 回路量子操作的极大潜力。

图17 利用SPEs 与金属纳米线强耦合实现单光子晶体管的设想［140］Fig.17 The proposal of a single-photon transistor using the strong coupling between the SPEs and metal nanowires［140］

图18 银纳米线-蝴蝶结结构用于高空间分辨率的量子比特操控［141］Fig.18 Manipulation of the qubits with high-resolution using an AgNW-bowtie hybrid structure［141］

SPP 集成回路中能够通过电学方法直接实现对量子SPP 的测量［142-144］，但是银纳米线在这类工作中一般扮演被探测的SPP 载体而非探测器的角色，如银纳米线上SPP 的电场激发锗纳米线产生电子空穴对，从而形成电流被直接探测［142］。或将银纳米线或其他SPP 波导置于超导探测器上，也是常用的高灵敏SPP 测量方式［143-144］，这些方法都是采用电学方式直接对SPP 进行测量而非转化为光子作为辅助，证明了搭建包括产生、操作到测量的完整超紧凑量子SPP 集成回路的可行性，而银纳米线在其中必能由于自身独特优势而发挥重要作用。

3.2.3 当前困难和可能发展

利用银纳米线搭建量子集成回路的最大困难仍然体现在较高的传输损耗上，它不可忽略地影响了其中SPP 量子性质的保持和传递，进而极大限制了大型和复杂化量子集成SPP 回路的搭建。为了保持严格场束缚的同时降低SPP 的欧姆损耗，杂化SPP 波导结构被提出和引入实验。不管是银纳米线作为天线，将SPP耦合至介质波导中进一步远距离传输；或是使得杂化SPP 的模场大部分位于介质材料中，从而降低损耗实现更长的传播距离，都能够有效减少银纳米线自身SPP 本征传输模式的损耗影响。另一方面，由于银纳米线上SPP 对介质环境表现出强烈的依赖性，因此可以通过改变周围介质的介电常数来调节银纳米线上SPP的特性，尤其是如果引入折射率能够进行主动和可逆调谐的介质材料，有望实现各种高性能的SPP 器件。除此之前，采用增益材料的补偿方案，和新颖的纳米线制作技术也有待进一步研究。总体来说，将银纳米线与纳米光子和纳米电子器件相结合，将能够在量子SPP 集成回路的发展中发挥重要作用。

3.3 银纳米线用于量子精密测量

3.3.1 相关理论和实验

银纳米线上紧束缚的SPP 模式天然具有突破衍射极限的超分辨能力，而SPP 模式内较大的态密度又能有效增强相互作用，对各种线性及非线性光学过程进行放大，因而银纳米线在提高传感和测量的空间分辨率、增强信号对比度上都是极有优势的工具［145］，在经典光学领域中已经被应用于针尖增强拉曼散射［146-147］、单细胞荧光温度计［148］、压力传感［149］、折射率变化传感［150］、Hg2+离子浓度传感［151］等各种传感和测量工作中。量子信息技术和量子光学的高速发展也为光学传感、测量和成像提供了一个新平台和途径，多种特殊测量技术［152-153］和包括使用非经典态作为光源等新型实验方法［154-156］，被开发出来进一步提高了传感和测量的性能，并成为一个新的研究方向——量子精密传感/测量。因而将天然具有亚波长尺寸的银纳米线SPP，与量子精密传感/测量方法相结合，即有可能实现空间分辨率与测量灵敏度同时提高，甚至超越经典极限的传感、测量和成像。

用单发光点作为纳米点状探针对银纳米线进行精准扫描，利用SPP 与SPE 之间局域相互作用，通过测量SPE 状态的变化，如自发辐射速率、寿命分布等，能够进一步分析得到银纳米线亚波长范围内局域态密度的超分辨分布图［157-158］，如图19、图20 所示。虽然在这些工作中，银纳米线是作为产生被测量电磁场的待测物，但这些实验方案完全可以反过来，将银纳米线作为纳米探针［87］，将SPEs 或其他量子发光体作为待测物，同样能够得到突破光学衍射极限，并且高衬比度的传感和成像。由此可见一根灵活、位置精确可控的银纳米线，再加上其中传输的具有量子性质的SPP，在量子精密传感、量子成像等应用中大有可为［129］。采用某些特殊的量子SPP 态能够从原理上突破噪声极限，提高测量灵敏度。以样品吸收率/透过率的测量和成像为例，其物理模型可以理解为一束作为光源的照明光子态和一个真空态，同时从不同方向入射一个透过率为η的BS 后，透过的光束被接收和探测的过程［159-160］。该过程在量子光学中能够以玻色产生湮灭算符的形式表示，对应的透射湮灭算符和反射湮灭算符可分别表示为

图19 利用银纳米线上SPP 对NV 色心寿命调制实现超分辨局域态密度测量［157］Fig.19 Quantitative analysis of the LDOS with super-resolution via the manipulation of NV-centers′lifetimes by AgNWs［157］

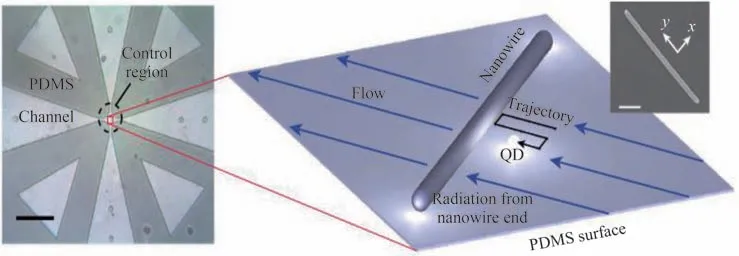
图20 利用银纳米线上SPP 与单量子点之间相互作用实现超分辨成像［158］Fig.20 Super-imaging realized by the interaction between a single QD and the SPP of AgNW［158］

光纤锥-银纳米线杂化结构就是一根天然的适用于量子精密测量和成像的探针，将其组装进商业近场扫描系统，并激发其中的量子SPP 即可实现量子近场测量和成像。值得一提的是，法诺因子F在经过一个效率为ηc的光路后，最终探测到的光子态法诺因子会退化为Fdet=ηcF+1-ηc，因此哪怕对于一个理想的Fock 态照明光源，经过损耗后仍然有Fdet=1-ηc。这里的ηc不仅表示之前物理模型中的样品自身透过率，更包括整个过程光路中的各种损耗以及探测效率。因此损耗在量子测量和量子成像中的影响不可忽略，因为损耗会造成量子态的退相干，带来真空涨落的噪声。所以利用透过率一般在10-5量级的传统商业近场探针传输量子态，以期达到同样的目的并不可行，进一步提高光纤锥-银纳米线这一结构，或者其他新型近场光学探针的整体效率更为实际和有意义。文献［87］和［128］都已经报道了利用这种杂化结构作为真实近场探针，对样品进行近场光学扫描成像的工作。并且这两个工作中都实现了远超商业探针的光学效率，向着未来利用该结构真正实现同时突破光学衍射极限，和散粒噪声极限的量子近场显微镜的目标更进一步。

3.3.2 当前困难和可能发展

目前真正将银纳米线应用于量子精密测量的工作还寥寥无几，这主要由于该目标要求的各种条件，包括SPP 保持良好的量子性质、SPP 模式体积突破衍射极限到纳米尺寸，以及对待测样品和探针直接实现灵活而精准的操控等等，在实验上难以同时满足。更小的模式体积一般需要更细的银纳米线，但这会带来更大的传输损耗和要求更高的控制精度，而大传输损耗则不利于量子性质的保持。另一方面来说，某些特殊的量子态在银纳米线上的传输，如偏振纠缠态的量子性质一般需要通过银纳米线的高阶模进行保持，但高阶模则对应更弱的能量束缚和更差的空间分辨率。对银纳米线实现灵活而精准的一系列微纳机械操作，如任意移动、纳米级定位等也要求更优秀的工程技术和实验方案。类似的，这些困难也可能通过银纳米线与其他介质纳米器件耦合的杂化系统加以克服。通过尽可能提高耦合效率，降低光学损耗，采用合适的自由度编码量子信息等方面进行优化，银纳米线在量子精密测量上进行实际应用依然潜力无限。

4 总结与展望

本文梳理了银纳米线在量子光学领域的相关研究进展，从银纳米线上SPP 的基本光学性质和量子性质开始，重点介绍了银纳米线纳米级的SPP 模式体积、较高的模式密度，以及能够对光子量子特性进行良好保持和传输的特点和突出优势。这些性质为银纳米线在量子光学的广泛应用提供了基础，在与量子发光点相互作用方面，弱耦合机制下能够实现具有更优良性质的量子光源，在强耦合机制下能够实现多个发光体之间的量子纠缠；利用银纳米线中SPP 之间或与其他物质之间的线性和非线性相互作用能够实现各种量子操控，从而实现超小型集成量子SPP 回路的搭建；而将银纳米线能够突破光学衍射极限的优势与量子计量能够突破散粒噪声极限的优势相结合，应用在传感和测量成像，有望实现分辨率和灵敏度的同时提高。

然而，SPP 的许多量子特性仍然有待更深入的研究，在利用银纳米线实现真正可实用化的量子器件过程中，许多问题仍有待解决。在对不同应用的具体单独介绍中，都可以发现银纳米线上SPP 损耗所带来的影响和限制，这也是其他等离激元器件共同面临的问题。对于降低SPP 的传输损耗，可以通过采用吸收尽可能小的材料如石墨烯等实现长程SPP［161］。近年来也有些工作指出损耗可以通过在SPP 波导附近加入增益介质来进行补偿［162］，但这些工作仍是在经典光学范畴进行研究的，该技术可能会影响量子态在传输中的相干性质。目前来看，将银纳米线与介质波导耦合形成杂化量子系统还是最为有效和实际的的途径，以平衡损耗与束缚的关系［79，163-164］。但从另一方面讲，利用SPP 损耗，研究其特殊的耗散效应也是未来的一个研究方向［165］。银纳米线容易在空气中发生氧化是另一个实际应用中的挑战，创造一个无氧工作环境显然需要较高的成本，很多场景下也难以适用。目前常用的方法是在银纳米线外包裹一层其他稳定材料防止氧化［166］，但这可能会在某种程度上削弱局域效果，尤其是对小直径银纳米线影响尤甚。除了对这些亟待解决的挑战的探索，未来银纳米线在量子光学中的研究可能会朝着复杂化和级联化发展，如与多个SPE、多种其他微纳光子器件、或是多根银纳米线之间的相互作用和集成。同时从控制银纳米线上SPP 的强度、偏振、路径等相对较简单的特性之后，进一步利用银纳米线携带矢量化和具有更高维度量子信息的研究也已经开始。进一步增强银纳米线与各种量子发射体之间的相互作用，以至实现强耦合的实验研究也仍然会是热门方向。为了实现这些目标，除了需要对等离激元量子特性更深刻的理论理解之外，对银纳米线自身的基本性质研究和制作工艺也需要相应跟上，如对其介电常数更多的理论和实验研究［167］，更精准控制银纳米线尺寸的相关工艺，和制备或加工具有特殊端面形状，如锥形针尖的银纳米线［168］，用纳米颗粒甚至多个纳米颗粒对银纳米线进行修饰等等。探索这些令人兴奋的新兴前沿领域和寻找解决这些问题的答案，必定能使银纳米线在量子光学中的研究进入到一个全新而富有成效的阶段，在更多的实际应用中大放异彩。