隔震支座对高速铁路简支梁桥地震易损性的影响研究
汤兴文


【摘要:】为研究隔震支座对高速铁路简支梁桥地震易损性的影响,文章采用OpenSees软件建立三维隔震与非隔震高速铁路简支梁桥精细化有限元模型,并采取增量动力分析(IDA)方法,以符合工程场地情况的地震动作为输入,对有限元模型进行时程响应分析,獲得了支座和轨道结构的地震易损性曲线。研究结果表明:在横向地震下,采用隔震支座能够有效降低滑动层的失效概率,最大可降低60%左右;由于滑动层的地震耗散作用,CA层和扣件在横向地震下失效不明显。
【关键词:】铁路桥梁;易损性曲线;数值计算;隔震支座;简支梁桥;OpenSees
U442.5+5A471564
0 引言
近年来,我国高速铁路建设飞速发展,截至2018年年底,已经建成“四纵四横”铁路网[1],总里程达2.9万km。预计到2025年,铁路网规模达到17.5万km左右,其中高速铁路3.8万km左右,基本覆盖我国主要人口居住区[2]。然而,随着高速铁路线路的增加,势必会通过一些高烈度高风险的地震区域,因此有必要对高速铁路中常见的简支梁桥进行抗震性能分析,为高烈度地震区域的铁路桥梁设计提供一定的参考。
进行桥梁抗震性能分析时,一个比较直观及方便易懂的方法就是建立地震易损性曲线,目前公路桥梁地震易损性曲线研究已经比较成熟[3],公路桥梁与铁路桥梁一个最明显的区别就是铁路桥梁受到上部轨道结构约束的影响。杨平等[4]以川藏铁路为研究对象,对某不等高墩简支梁桥进行了地震易损性分析。周长东等[5]针对多跨连续钢筋混凝土桥,采用汶川地震动和NGA强震数据库提供的地震波,分析了该类铁路桥在地震作用下的地震易损性。以上文献仅针对桥梁本身,并没有考虑轨道约束对铁路桥梁地震易损性的影响。随后,魏标、Cui[6-8]等针对这一问题,建立了考虑轨道约束的铁路桥梁有限元模型,进行了地震易损性分析。总体来说,考虑隔震情况下,即关于铁路桥梁考虑轨道约束的地震易损性研究还相对较少,因此有必要开展相关研究工作。
基于此,本文针对高速铁路简支梁桥,通过OpenSees软件建立考虑轨道约束的隔震与非隔震铁路简支梁桥有限元模型,采用IDA分析方法,以符合工程场地情况的地震动作为输入,来研究隔震支座对高速铁路简支梁桥地震易损性的影响。
1 地震易损性分析方法
地震易损性是指在不同强度的地震作用下结构发生某一破坏状态的超越概率[9],可以用式(1)进行表示[6]:
Pf=P[D≥C|IM](1)
式中:Pf——超越概率;
C——损伤状态能力极限;
D——结构的地震需求;
IM——地震动强度(如地面峰值加速度PGA)等)。
若假定工程需求参数的中值(Sd)与IM满足如下指数关系:
ln(Sd)=lna+blnIM(2)
式中:a和b——回归系数。
如果假定易损性曲线为对数正态累积分布函数,则易损性函数可表示为[10]:
Pf=ln (Sd/Sc)β2Sd|IM+β2c(3)
式中:Sc和βc——结构抵抗破坏状态能力的中位值和结构抵抗破坏状态能力的对数标准差;
βSd|IM——Sd在给定的IM条件下的对数标准差。
结合式(2)、式(3)可进一步改写为[11]:
Pf=lna+blnIM-lnScβ2Sd|IM+β2c(4)
式(4)即为所求的地震易损性曲线概率公式。根据Hwang[12]建议,若IM取为PGA时,β2Sd|IM+β2c=0.5。
2 工程案例
2.1 桥梁概况
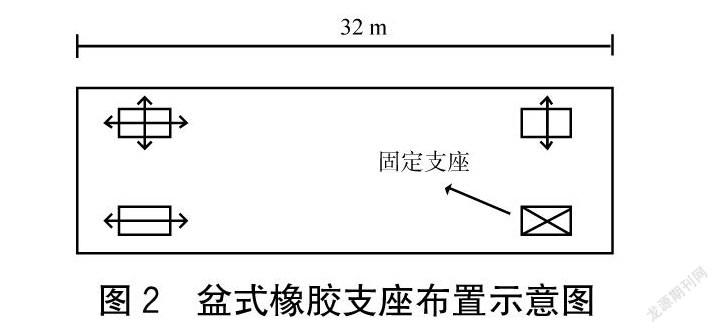
以一座常见的四跨(32+32+32+32)m高速铁路简支梁为例进行分析,桥梁布置如图1所示。主梁采用C50混凝土,主梁为箱型截面,桥面宽12 m。桥墩墩高一致,为16 m,采用C30混凝土,桥墩类型为矩形重力式桥墩,截面宽度为7 m×3.2 m。支座共采取两种形式:LRB500铅芯橡胶隔震支座和盆式橡胶支座。在一跨主梁内共布置四个支座。盆式橡胶支座布置如图2所示。
桥上无砟轨道类型为CRTS-Ⅱ无砟轨道,包括滑动层、砂浆层、轨道板、底座板、扣件、钢轨等构件。轨道板、底座板在桥上纵向连续。
2.2 有限元模型
采用OpenSees软件建立隔震(铅芯橡胶支座)与非隔震(盆式支座)桥梁轨道有限元模型,力学简图见图3。对于桥梁结构,主梁采用弹性梁单元模拟,桥墩采用非线性梁柱单元,混凝土为Ken-Park本构模型[13],其中核心混凝土采用OpenSees材料库中的Concrete02本构,保护层混凝土采用Concrete01本构。无论盆式橡胶支座还是铅芯橡胶隔震支座都采用零长度单元模拟,其中盆式橡胶支座根据规范[14]中的规定其力学恢复力为理想弹塑性模型,而铅芯橡胶隔震支座为双线性
恢复力模型[15]。对于轨道结构,钢轨、轨道板、底座板采用弹性梁单元模拟,扣件、CA砂浆层、滑动层采用零长度单元模拟。扣件、CA砂浆层、滑动层具体参数取值见文献[16]。隔震(铅芯橡胶支座)与非隔震(盆式橡胶支座)模型仅在支座上有区别,其他构件均为一致。
2.3 地震动输入
该桥梁工程场地类型为二类,根据《建筑抗震设计规范》(GB 50011-2016)的规定求得二类场地规范反应谱,然后根据规范反应谱从美国太平洋地震工程中心(PEER)选取5条符合实际工程场地的地震波,见图4。分别调整各组地震动记录的峰值加速度PGA为0.1~1 g,增量为0.1 g,然后再输入图3中OpenSees有限元模型进行增量动力时程分析(IDA)[17]。地震动输入方向为横桥向,共得100种工况。4B4B2C53-3603-4BBD-9438-556F2FA071AE
2.4 損伤指标
在计算地震易损性曲线时,还需要确定各构件的损伤状态,本文主要考虑支座以及轨道结构的易损性。因此,将各构件的损伤状态限值列于表1[6]。LRB500铅芯橡胶支座橡胶层厚度为75 mm,根据文献[18]中的定义,将225 mm作为完全破坏界限。
3 横向地震下地震易损性曲线
通过对有限元模型的时程响应进行分析,发现CA层、滑动层、扣件位移出现最大位置为梁缝处,因此本文研究重点是梁缝处的各构件地震易损性。支座同样是选取各支座在横向地震下的位移最大值(3号墩活动方向)。
3.1 滑动层地震易损性曲线
利用时程分析结果,并结合式(4)即可求出两种不同模型(隔震与非隔震)的滑动层地震易损性曲线,见图5。由图5可知,当采用隔震支座时,无论在何种损伤状态下,滑动层的失效概率明显降低。尤其对于完全破坏而言,当PGA=1 g时,隔震支座下的滑动层失效概率仅为40%左右,而非隔震支座下的滑动层失效概率达到100%,相差60%左右。因此,采用隔震支座将能明显降低滑动层的失效概率。
3.2 CA层及扣件地震易损性曲线
无论是隔震情况还是非隔震情况,CA层和扣件在横向地震下的位移反应不明显[6-7],即隔震支座对CA层和扣件的地震位移影响较小。这主要是由于滑动层能迅速消散地震能量,以保护上部轨道结构免受地震破坏。
3.3 支座地震易损性曲线
同理求得支座地震易损性曲线,见图6。
由图6可知,隔震支座的失效概率均大于非隔震支座的,但两者之间相差并不大。究其原因,主要是在横向地震下隔震支座通过自身位移能够耗散较多的地震能量,有效地减少了往上部结构传递的地震力,从而使得滑动层的失效概率明显降低,达到了保护上部结构免受地震损坏的目的。
4 结语
本文通过OpenSees软件建立四跨隔震与非隔震铁路简支梁桥有限元模型,然后选取符合工程场地的地震动作为输入,得到了一系列非线性时程响应结果,并利用时程响应结果计算了各构件的地震易损性曲线。主要得到以下结论:
(1)在横向地震下,采用隔震支座能够有效地降低滑动层发生失效的概率,尤其是完全破坏。当PGA=1 g时,能够降低60%左右的失效概率。
(2)就本算例而言,CA层和扣件在横向地震下失效概率不明显。究其原因,主要是在地震作用下,滑动层的迅速滑动消散了地震能量,从而对轨道结构起到一定的保护作用。
(3)在本算例中,无论何种破坏状态下,隔震支座的失效概率都大于非隔震支座的,但上部轨道结构滑动层的失效概率都小于非隔震情况。究其原因,主要是隔震支座通过自身位移耗散地震能量,减少了地震力往上部结构传递,从而对上部结构起到保护作用。
参考文献:
[1]勾红叶,杨龙城,蒲黔辉,等. 高速铁路桥梁横向变形与单元板式无砟轨道钢轨变形的映射关系 [J]. 中国铁道科学,2019,40(5):42-52.
[2]蓝 兰. 未来十年铁路投资继续高位运行 高铁里程翻倍 [J]. 工程机械文摘,2016(5):67-70.
[3]李宏男,成 虎,王东升. 桥梁结构地震易损性研究进展述评 [J]. 工程力学,2018,35(9):1-16.
[4]杨 平,杨国静,曾永平. 川藏铁路简支梁桥地震易损性及适应性分析 [J]. 铁道工程学报,2015,32(12):51-57,75.
[5]周长东,王京京. 铁路桥梁的地震易损性分析 [J]. 北京交通大学学报,2014,38(4):101-106.
[6]魏 标,杨添涵,蒋丽忠. 轨道结构建模精细化程度对高速铁路连续梁桥地震易损性的影响 [J]. 工程力学,2018,35(4):16-2 51.
[7]WEI B,LI C B,HE X H. The Applicability of Different Earthquake Intensity Measures to the Seismic Vulnerability of a High-Speed Railway Continuous Bridge[J]. International Journal of Civil Engineering,2019,17(7A):981-997.
[8]CUI S G,GUO C,SU J,et al. Seismic Fragility and Risk Assessment of High-speed Railway Continuous-Girder Bridge under Track Constraint Effect [J]. Bulletin of Earthquake Engineering,2019,17(3):1 639-1 665.
[9]吕大刚,刘 洋,于晓辉. 第二代基于性能地震工程中的地震易损性模型及正逆概率风险分析 [J]. 工程力学,2019,36(9):1-1 24.
[10]CORNELL CA,JALAYER F. Probabilistic basis for 2000 SAC Federal Emergency Management Agency Steel Moment Frame Guidelines[J]. Journal of Engineering Structures,2002,128(4):526-533.
[11]MACKIE K,STOJADINOVIc'B. Probabilistic Seismic Demand Model for California Highway Bridges[J]. Journal of Bridge Engineering,200 6(6):468-481.4B4B2C53-3603-4BBD-9438-556F2FA071AE
[12]Hwang H,Liu J B,Chiu Y H. Seismic fragility analysis of highway bridges[R]. MAEC report:project MAEC RR-4. Urban:Mid America Earthquake Center,2001.
[13]KENT D. Flexural members with confined concrete [J]. Journal of Structural Division Asce,1971(97):1 969-190.
[14]JTG/T B02-01-2008,公路橋梁抗震设计细则[S].
[15]陈 列,胡京涛. 桥梁减隔震技术 [M]. 北京:中国铁道出版社,2014.
[16]GUO W,HU Y,HOU W,et al. Seismic Damage Mechanism of CRTS-II Slab Ballastless Track Structure on High-Speed Railway Bridges [J]. International Journal of Structural Stability and Dynamics,2020,20(1):1-26.
[17]VAMVATSIKOS D,CORNELL CA. Developing Efficient Scalar and Vector Intensity Measures for IDA Capacity Estimation by Incorporating Elastic Spectral Shape Information [J]. Earthquake Engineering & Structural Dynamics,2005,34(13):1 573-1 600.
[18]ZHANG J,HUO Y L. Evaluating Effectiveness and Optimum Design of Isolation Devices for Highway Bridges Using the Fragility Function Method[J]. Engineering Structures,2009,31(8):1 648-1 660.4B4B2C53-3603-4BBD-9438-556F2FA071AE

