基于含时微扰理论的电场中一维线性谐振子跃迁几率研究①

庞福荣, 张澜旭, 温 莹, 张海丰,*

(佳木斯大学a.理学院,b.机械工程学院,c.药学院,黑龙江 佳木斯 154007)

0 引 言

含时微扰理论是量子力学问题研究中重要的近似方法之一,因而被物理、化学、生物等学科理论研究和量化计算广泛的应用[1-4]。另外,由于物质中原子、分子等微观粒子的热振动作用往往近似利用谐振子物理模型来处理,使得谐振子模型也被广泛的应用到多学科的数学建模中[5-8]。旨在给出含时微扰理论的跃迁概率公式,进而讨论绝热近似情况的跃迁概率,确定绝热近似处理问题的条件;研究在恒定弱电场和指数变化电场中一维线性谐振子的一阶跃迁概率。

1 一阶含时微扰下的跃迁概率

将(1)和(2)式带入(3)式,并用＜φn|左乘可得

考虑到跃迁发生在不同的状态之间,所以

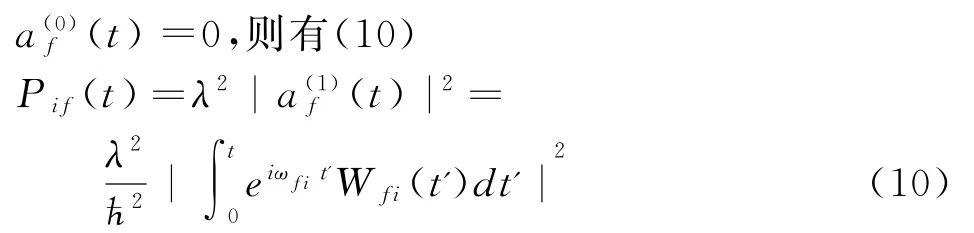
2 绝热近似下的跃迁概率

取一个角频率为ω ,电荷为e的一维谐振子。若

3 恒定弱电场中的一阶跃迁概率

若在t=0时处于基态,在τ 时间段内被施加一个恒定弱电场沿x 轴正方向,电场强度为ε ,则体系的微扰算符为则按照一阶含时微扰论可得从基态到n=1态的跃迁概率P01为

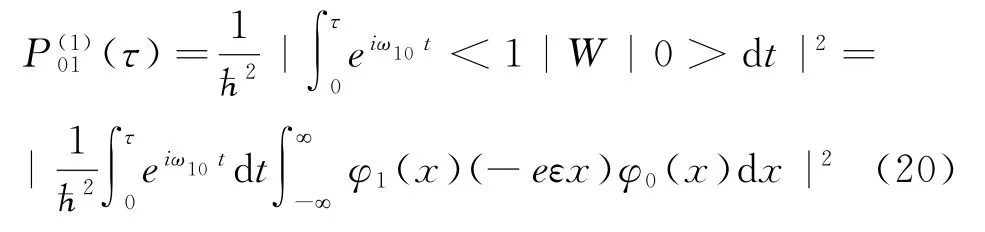
式(20)中:φ0(x)和φ1(x)分别为能量算符的基态和第一激发态,即

4 指数变化电场中的跃迁概率

设在任意时刻,一维线性谐振子被施加一个指数变化的电场

式(26)中:A 是常数。由外场的时间积分可知,动量增量p 为

即在一阶微扰下,均匀场只能诱导出基态到第一激发态的跃迁。

5 结 论

从上边的推导可知,对于给定的经典动量 增量p,激发概率随时间增加而减少。