负载和输入电压自适应零电压软开关全桥变换器

杨晓光 王德鑫 贾 哲 高 正

负载和输入电压自适应零电压软开关全桥变换器

杨晓光1,2王德鑫1,2贾 哲1,2高 正3

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130 2. 河北工业大学河北省电磁场与电器可靠性重点实验室 天津 300130 3. 上海空间电源研究所 上海 200245）

该文提出一种在宽输入电压和宽负载范围内工作于零电压软开关（ZVS）的全桥DC-DC变换器。该变换器是在传统移相全桥变换器拓扑的基础上增加了一个简单的LC辅助电路，并通过窄频率调节方式控制辅助电流，在满足ZVS条件下能够最小化环流损耗。采用窄频率变化能够对辅助电流进行有效的调节而不会对主电路的设计和控制带来明显的影响。对变换器的稳态性能进行详细分析；建立变换器的数学模型，可直接用于变换器的优化设计和精确控制。实验结果与理论分析具有很好的一致性。

环流损耗 全桥变换器 负载自适应 输入电压自适应 谐振电路 零电压软开关（ZVS）

0 引言

隔离型零电压软开关（Zero-Voltage-Switching, ZVS）移相全桥（Phase-Shifted Full-Bridge, PSFB）变换器广泛用于各类DC-DC能量变换系统中。PSFB变换器工作于ZVS时能够消除开关损耗，避免开关噪声对控制电路的影响并具有出色的电磁兼容（Electromagnetic Compatibility, EMC）性能。

传统PSFB变换器的缺点是，在轻载条件下难以实现ZVS。但在很多应用中，变换器需要长时间运行于轻载状态[1-6]，因而需要提出新的方法来拓展PSFB变换器的ZVS范围。

拓展ZVS范围最直接的方法是增加漏电感[7]或在变压器的一次侧串接电感[8]。但是，这种方法会导致有效占空比降低、环流损耗增大、变换器功率传输能力受限以及二次侧振荡变大等问题。

目前已经提出了许多方法来拓展PSFB变换器的ZVS范围，例如，双半桥变换器[9-10]、不同变换器的组合[11-12]以及一些新的控制方法[1, 4, 13-14]。在这些解决方案中，增加无源辅助电路的方法具有简单、鲁棒、成本低等优点，受到了广泛的关注[15-23]。

最简单的无源辅助电路仅包含一个电感，并联于变换器桥臂的中点[18]。这类变换器可以在轻载条件下利用辅助电流实现ZVS，但在重载条件下环流损耗过大。文献[3, 19-20]中改进的感性辅助电路所产生的辅助电流与负载条件无关，从而降低了环流损耗。文献[24-25]中所提出的变换器采用耦合电感作为辅助电路，所提供的辅助电流能够自适应负载的变化，从而极大地降低环流损耗。

与文献[3, 18-20, 24-25]中的感性辅助电路相比，文献[26-27]中的谐振型辅助电路所产生的环流损耗会更小。这是因为谐振型辅助电流在开关暂态期间具有很大的峰值，而在其他时间具有较小的值，当提供相同能量满足ZVS条件时，这种谐振电流的方均根（Root-Mean-Square, RMS）值远小于电感型辅助电路产生的三角波或梯形波的RMS。具有并联电感型辅助电路或谐振型辅助电路的移相全桥变换器，可通过控制开关频率进一步降低环流损耗[3, 23, 26-27]。

本文提出了一种辅助电流随着输入电压和负载变化而自适应变化的ZVS移相全桥变换器，该变换器能够在整个输入电压范围和负载范围内实现ZVS，并具有较小的环流损耗。本文的主要贡献为：①较之添加额外并联电感辅助电路的解决方案[3, 18-20, 24-25]，本文利用励磁电感作为辅助电路的组成部分，节省了磁性器件；②建立了变换器的数学模型，能够准确描述辅助电流与输入电压、负载电流和开关频率的关系，可直接用于变换器的优化设计和精确控制；③增加的LC电路结构简单、便于设计，能够显著降低变换器的环流损耗。

本文首先介绍变换器的拓扑和工作原理；然后将给出移相角和开关频率对变换器增益、输出电流和电感电流的影响以及ZVS的实现条件；接着通过设计实例给出变换器工作于自适应频率模式的详细设计过程；最后通过测试结果验证理论分析的准确性。

1 工作原理

具有并联电感辅助电路的变换器漏电感leak可以设计得足够小以减少其负面影响[18]。若leak足够小，其影响可以忽略，从而可将并联单电感辅助电路集成到变压器中。

本文采用励磁电感m代替单电感辅助电路为变换器实现ZVS提供能量。但是，具有并联单电感辅助电路的变换器的缺点是重载情况下具有较大的环流损耗。为了减少环流损耗，本文在全桥变换器中增加了一个串联LC电路和励磁电感共同组成辅助电路。所提出的PSFB全桥变换器如图1a所示。开关S1～S4的等效电容等于开关的寄生电容和其他杂散电容之和，分别由1～4表示。图1a中，in为输入电压，VD1～VD4为二极管，f为滤波电感，f为滤波电容，o为负载电阻，p为辅助支路电容，p为辅助支路电感。

图1 全桥变换器及其等效辅助电路

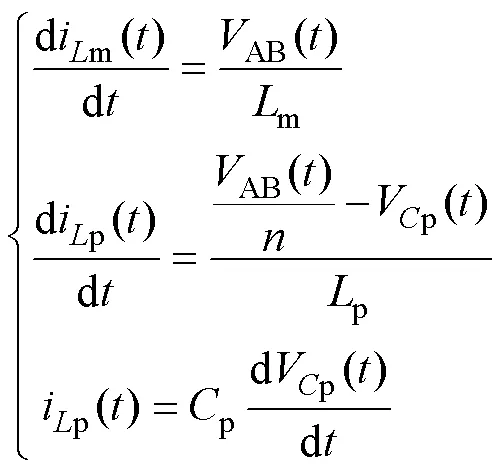
根据式（1）和式（2），将LC电路反射到变压器一次侧，可以建立用以分析辅助电流的等效电路，如图1b所示，由图1b可知，a()为

本文所提出的变换器的关键波形如图2所示，图中，a 为VA和VB之间的移相角（rad）。这四种情况的分析类似，所以本文只详述a＜p/2的情况。

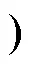
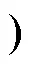
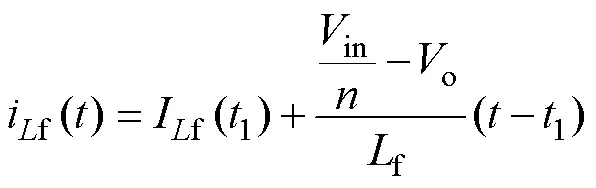
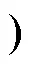
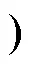
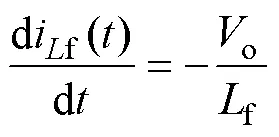
后半周期[4,8]的分析与前半周期相同，此处不再赘述。

2 变换器稳态分析

2.1 辅助电流

本节主要分析辅助电流与移项角的关系以及辅助电流的频率特性，为后文移相角范围与变换器参数选择提供依据。

根据图2，im()和ip()在4的值分别与它们在0的值大小相等，方向相反，即

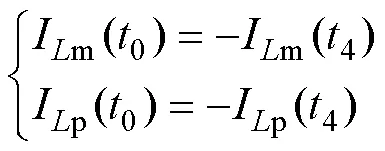
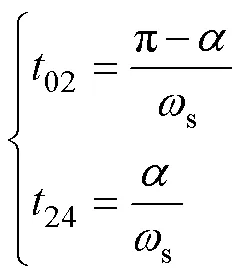
此处，定义变量

根据式（1）、式（8）和式（9），可得到im()在2和4的解以及ip()在2和4的解，分别表示为

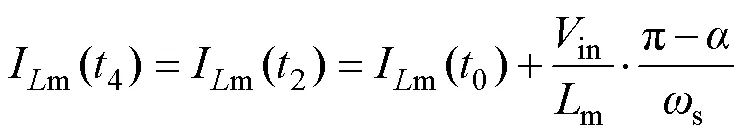
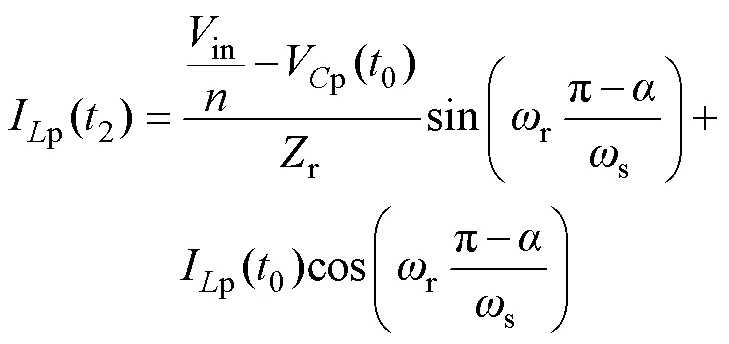
根据式（7）、式（10）～式（12），可解得im()和ip()在0时刻的表达式分别为

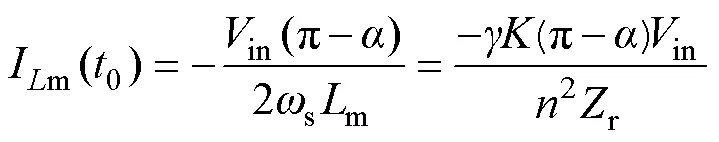
式中，=s/(2r)=r/(2s)；=2p/m。

本文引入归一化基准电压base和基准电流base，以简化对变换器特性的描述，分别定义为

从而，式（13）中的Im(0)和式（14）中的Ip(0)可以分别归一化为

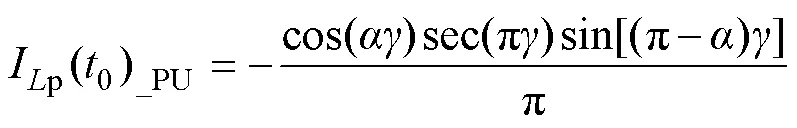
根据式（3）、式（16）和式（17），可得a()在0时刻的归一化值（见图2a）为

在不同值的情况下峰值电流与的关系如图3所示。式（16）和式（18）的计算结果分别如图3a和图3b所示，其中/=0.4。图3a表明，随着的增大，励磁电流在0时的值|Im(0)_PU|线性减小。虽然|a(0)_PU|在整个区间（0≤≤prad）随着的增加而减小，但在1rad≤≤2rad却基本保持不变。这意味通过增加一个简单的LC电路可以有效降低环流损耗。的最小值选择1rad时，变压器的利用率有所降低。如果选择的最小值为0.5rad，并且此时选择=0.8，这种情况下变换器的占空比接近传统移相全桥变换器的最大占空比，但在0.5rad≤≤1rad区间内环流损耗会有所增大。因此需要在环流损耗和变压器的利用率之间进行折中考虑。本文选择了1rad≤≤2rad这一区间。此外，通过对比图3a和图3b还可以看出，|a(0)_PU|对频率变化非常敏感，因而可以通过较小的频率变化来调整辅助电流的大小，以进一步减小环流损耗。

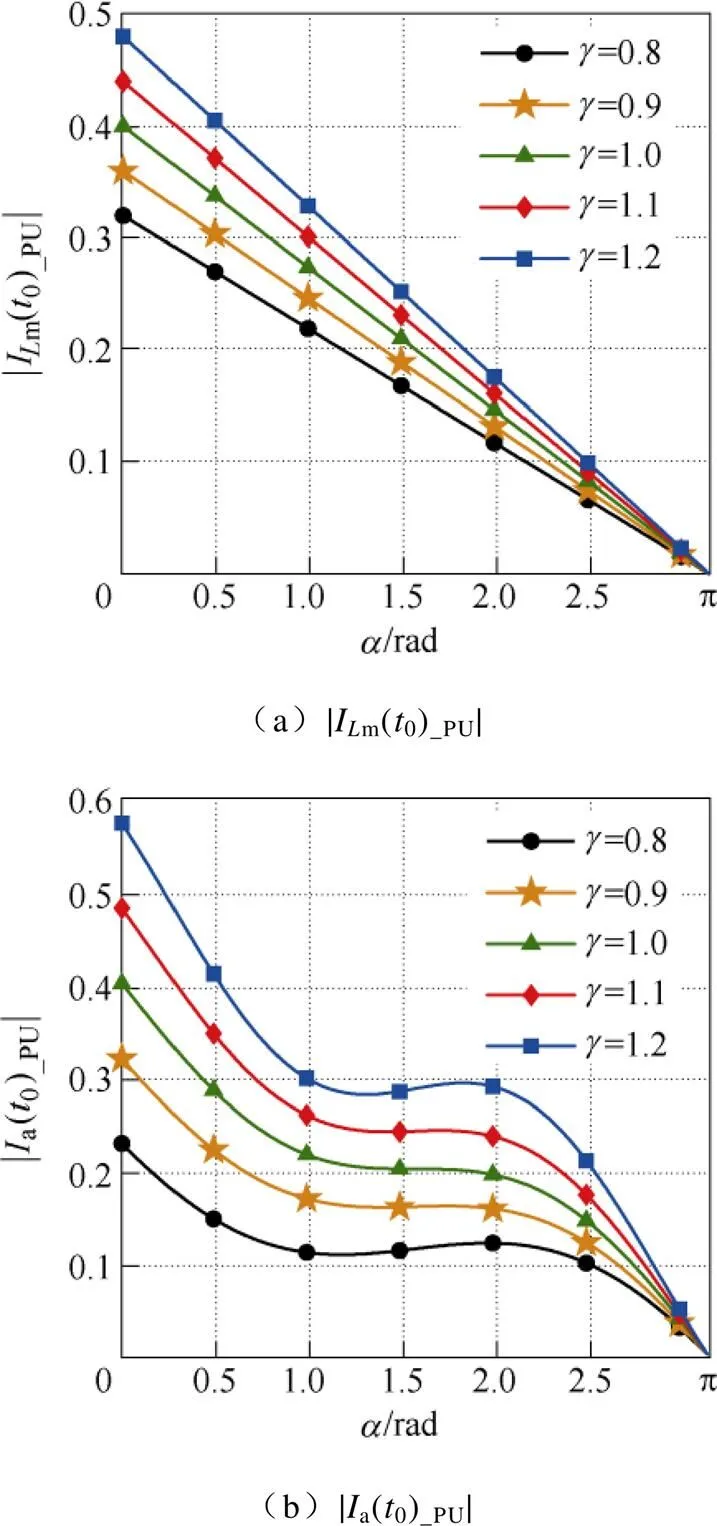
图3 在不同g 值的情况下峰值电流与a 的关系

需要注意的是，|a(0)_PU|的大小也依赖于/的值，当/较小时，式（18）中的Ip(0)_PU/起主要作用，使得|a(0)_PU|的非线性特性更强，此时，|a(0)_PU|具有更强的频率调整能力，但变化范围将变小；反之，当/的值选择较大时，|Im(0)_PU|将起到主要作用，|a(0)_PU|具有更大的变化范围，但其频率调整能力将弱化。因此，/的选择必须折中。根据计算结果，最终确定/的值为0.4。

2.2 主电路分析

本节主要分析移相角和开关频率对变换器增益、输出电流和电感电流的影响，为变换器的设计与控制提供依据。

用a表示与相关的占空比，e表示有效占空比。根据式（8），可得a=/(2p)。根据图2，e=02/s，a和e之和等于0.5，即

输入电压in和输出电压o的关系为

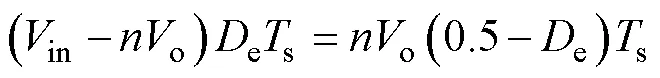
负载电流o等于电感电流If(0)和If(2)的平均值（见图2a），即

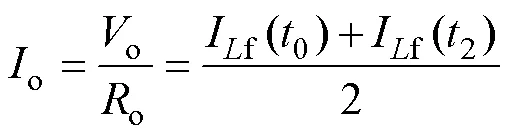
根据式（5）、式（6）、式（8）和图2a可得

由于leak足够小，滤波电感f足够大，由式（19）～式（22）可分别推导出变换器的直流电压增益以及滤波电感电流if()在0的值，分别为

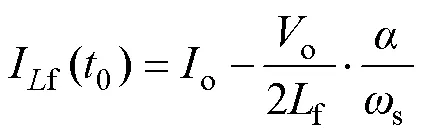
式（23）表明，本文所提出的变换器的直流电压增益可由移相角控制，与开关频率无关。由于滤波电感f的值足够大，窄频率变化对if()的影响可以忽略不计。需要说明的是：①本文中的窄频率调节范围远远小于谐振型变换器[28-30]的频率变化范围；②本文中的窄频率概念也不同于LLC变换器中类似说法，前者的变化范围远远小于后者[28]，微小的频率变化不会给变换器的设计和控制带来困难，这为辅助电流自适应频率工作模式提供了条件。

2.3 ZVS条件

开关实现ZVS分别取决于p(0)和p(2)（见图 2a）。在开关的瞬态过程中，p(0)和p(2)可以认为基本不变，根据式（1）、式（2）和式（4），滞后桥臂和超前桥臂实现ZVS开通的条件分别为

由于|If(0)|＜|If(2)|、|Im(0)|=|Im(2)|、|Ip(0)|=|Ip(2)|（见图2a），显然，只要辅助电流满足滞后桥臂的ZVS条件，超前桥臂必然能实现ZVS。因此，采用式（25）用于确保变换器在ZVS条件下运行。

3 设计过程

由2.1节可知：①可以通过窄频率变化来优化辅助电流以适应输入电压和负载电流的变化，从而最大程度地降低环流损耗；②窄频率变化不会给变换器的设计和控制带来困难。因而，本文所提出的变换器能够运行于自适应频率模式。本节通过表1的设计实例给出了自适应频率模式的详细设计过程，建立了精确的数学模型以描述辅助电流与输入电压、负载电流和开关频率的关系。

表1 变换器参数

Tab.1 Converter specifications

首先，需要根据移相角的变化范围确定变压器匝数比。根据2.1节的分析，当1rad≤≤2rad时，|a(0)_PU|的数值基本上与无关（与输入电压无关），并且可以通过窄频率变化进行有效调节以满足ZVS条件并使环流损耗最小化。考虑到实际电路中的压降，将最低输入电压（in=200V）对应的值设为1.18rad，考虑整流二极管的压降，式（23）改写为

将=1.18rad、d=1V、o=48V、in=200V代入到式（27），可得=2.5；再将=2.5、in=300V代入到式（27），可确定与最大输入电压（in=300V）对应的值为1.83rad。因此，最终确定工作范围为1.18rad≤≤1.83rad。假设变换器在整个输入电压范围内满载的%对应电流连续导通模式（Continous Conduction Mode, CCM）和电流断续导通模式（Dis- continous Conduction Mode, DCM）的临界值，满载的%以上工作在CCM，则输出电感f可表示为

式中，o_max=288W/48V=6A为最大负载电流；max=1.83rad为最大移相角。另外，式（28）也说明%越大（CCM的范围越小），输出电感f越小。理论上，变换器不能在整个负载范围内工作于CCM。

将式（23）代入到式（24），If(0)可表示为

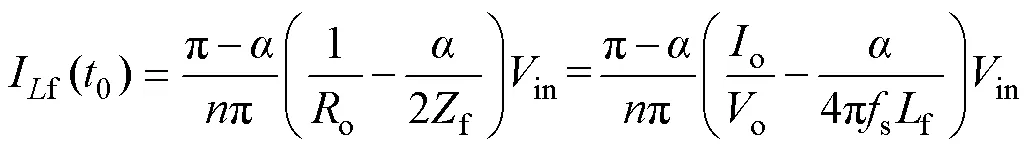
将式（13）、式（14）和式（29）代入到式（25）并结合式（28），ZVS条件可表示为

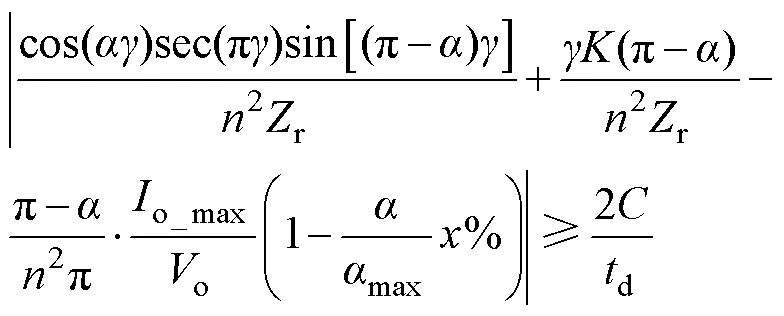
为了保证变换器在整个移相角范围内（1.18rad≤≤1.83rad）运行于ZVS，式（30）中的应该取最小值。将=1、=1.18rad、max=1.83rad、=2.5、=1、o=48V、o_max=6A、=0.8nF、d=150ns代入到式（30），可得LC电路的特征阻抗的最大值为

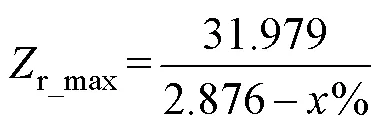
为确保变换器在整个输入电压范围内工作在ZVS条件下，LC电路的特性阻抗应小于r_max。

当变换器运行于DCM时，If(0)=0。在这种情况下，a(0)需要单独提供ZVS所需的电流。将式（13）、式（14）和If(0)=0代入式（25），可得变换器运行于DCM的ZVS条件为

从式（32）可以看出，当变换器工作在DCM时，其ZVS条件与负载无关，也和输入电压无关。将=1.83rad、=2.5、=1、=0.8nF、d=150ns和式（31）中的r_max代入到式（32），可得%与min之间的关系为

CCM临界值%与min的关系如图4所示。当变换器CCM范围变大（%减小）时，频率变化范围变大（min变小）。

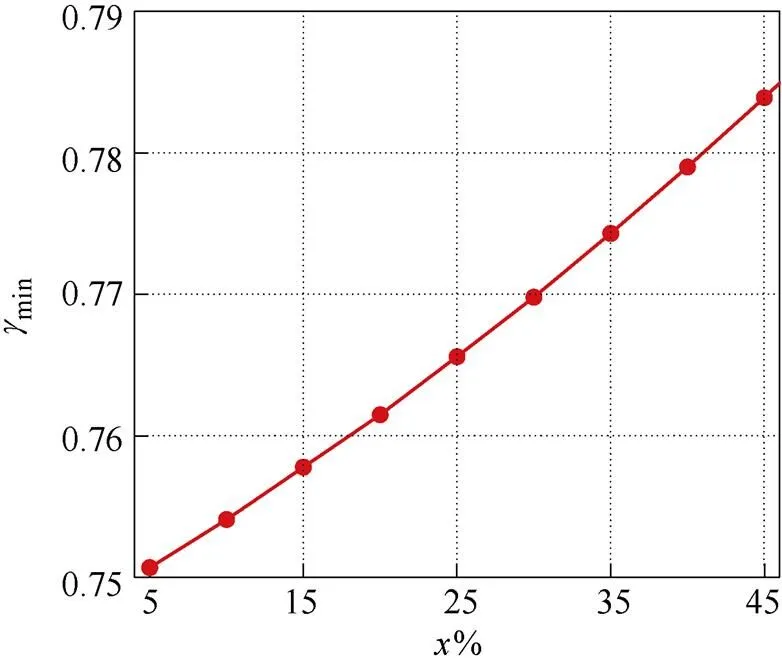
图4 CCM临界值x%与gmin的关系

当选择值后，将o=48V、s=100kHz、max= 1.83rad、o_max=6A代入式（28），可得出滤波电感的最小值f_min。本文为了分析变换器在宽负载范围内工作于CCM的特性，选择了较小的值。令=5可得，f_min=233mH。根据式（31），可计算出r_max的值为11.32W。输出电容f为

式中，DIf=2o_max×5%=0.6A。设计变换器的输出纹波电压D≤5mV。将DIf_max=0.6A、s=100kHz、D= 5mV代入到式（34），可计算出f=300mF。根据式（9）和=r/(2s)，p和p可分别表示为

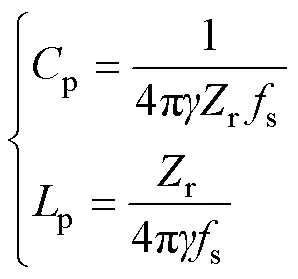
将s=100kHz、=1、r=11.32W代入到式（35），可得p=70nF,p=m/2=9.0mH。将=2.5、=1、r=11.32W、f=233mH、s=100kHz、=0.8nF、d=150ns代入到式（30），并将式（30）不等式变为等式，可得、o和三者之间的关系为

随o和的变化而自适应变化，以提供必要的电流来满足ZVS条件并最小化环流损耗，如图5所示。当输出电流o＜0.3A（小于5%的满载）时，变换器运行于DCM，在这种情况下，ZVS的实现条件与负载和输入电压无关（见式（32）），也就是和o与无关。当变换器运行于CCM时，可以根据式（36）随o和的变化（即负载和输入电压的变化）调整（开关频率）以提供必要的电流满足ZVS条件并最小化环流损耗。

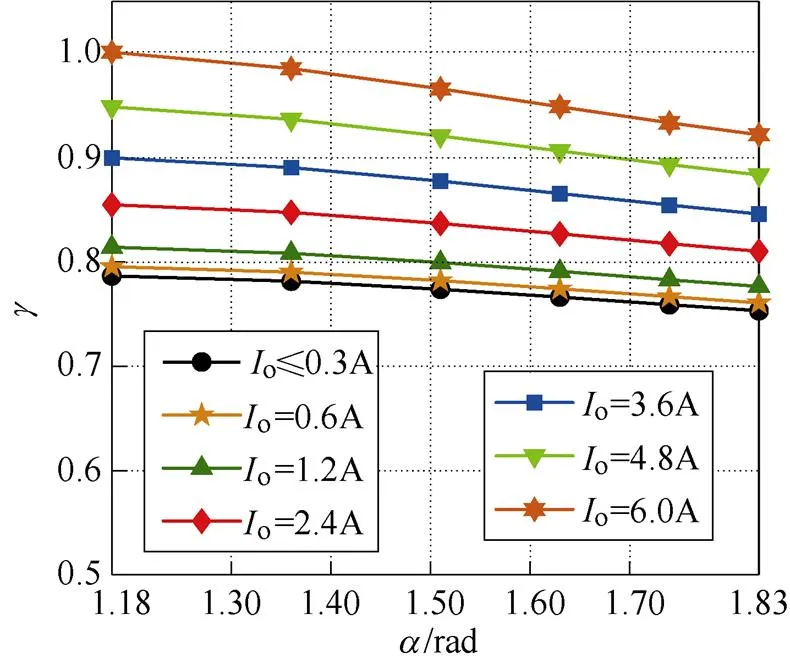
图5 g 随Io和a 的变化而自适应变化

根据式（2）、式（3）和式（15），对式（25）中的ZVS的条件进行归一化为如式（37）所示。根据式（15）和式（29），If(0)被归一化为如式（38）所示。

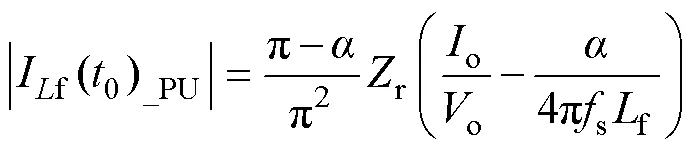
依据式（18）、式（37）和式（38）以及本节获得的相关参数，可得|p(0)_PU|作为、o和的函数表达式为

式（39）等号右侧部分表示满足ZVS条件所需的归一化电流，而左侧表示变换器能够提供的归一化电流。

当变换器工作在固定频率模式（s=100kHz，=1）时，|p(0)_PU|的计算结果如图6所示，图中，2r/(pd)=0.0961，表示满足ZVS条件所必须的归一化电流。当变换器的输入电压最小（in=200V，对应于=1.18rad）并且满载（o=6A）时，变换器ZVS运行所需的最小电流恰好等于变换器所能提供的电流，这种情况下变换器运行于ZVS条件并且环流损耗最小。当输入电压增大（增大）或/和负载减小（o减小），工作于固定频率模式下的变换器所提供的电流远大于ZVS运行所需的电流，从而导致环流损耗增大。当o＜0.3A（小于5%满载）时，变换器工作于DCM，在这种情况下，ZVS实现条件基本上与负载和输入电压无关（见式（32）），也就是和o与无关，此时|p(0)_PU|=|a(0)_PU|。正如所期望的那样，|a(0)_PU|在整个的输入电压范围内基本保持不变（200V≤in≤300V，对应1.18rad≤≤1.83rad，见图3b）。

图6 变换器工作于固定频率模式时（g =1），在不同负载电流Io条件下|Ip(t0)_PU|与a 的关系

根据式（36）和式（39），当变换器工作于自适应频率模式（见图5）时，|a(0)_PU|随着频率的变化而变化如图7所示，|p(0)_PU|的值能够根据输入电压变化负载变化而自适应地调整其大小。|p(0)_PU|在自适应模式下的计算结果如图8所示。与固定频率模式不同，变换器自适应频率模式下提供的电流非常接近ZVS条件所需的最小电流（2r/(pd)=0.0961）。因此，变换器工作于自适应频率模式时能提供满足ZVS条件所必需的电流并能够最小化环流损耗。

图7 变换器工作于自适应模式时|Ia(t0)_PU|与a 的关系

图8 变换器工作于自适应模式时|Ip(t0)_PU|与a 的关系

励磁电感m的实际值可能和设计值存在微小的偏差。这种偏差对变压器耦合系数的影响可以忽略不计[31]，即对变压器匝比的影响可以忽略不计。m的微小变化对LC谐振电路参数的影响也可忽略不计，其原因如下：①由式（13）可知，im()与m成反比；又由式（3）可知，a()为im()和ip()/的叠加；通过图3b可知，在1rad≤≤2rad这个区间，频率的变化对辅助电流具有很强的调节能力，足以弥补m的微小变化对辅助电流的影响。②根据式（9）和r/(2s)，LC电路参数的变化对于辅助电流的影响等价于和r的变化对辅助电流的影响。图3b表明，辅助电流峰值a(0)与基本呈线性关系。并且从式（3）、式（13）和式（14）可知，a(0)也与r呈线性关系。因此，LC电路中参数的变化与a(0)呈线性关系，LC电路参数的微小变化对峰值辅助电流的影响很小，不会对ZVS的实现造成困难。

这一部分参数的计算结果汇总在表2，根据计算结果最终所选择的实验样机参数也列在表2中。

表2 参数计算结果与实际参数

Tab.2 Parameters calculation and selection results

4 实验结果

分别在固定频率（s=100kHz，即=1）模式和自适应频率模式下对变换器进行了测试。测试过程中，输入电压由200V变为300V，负载由满载变为轻载（5%满载），实验结果如图9所示。

图9 变换器分别工作于固定频率模式（fs=100kHz）和自适应模式下的测试波形

测试结果验证了图2所示变换器工作原理的正确性。实验波形表明：①AB上升沿平滑并且没有较强的电压尖峰，因而在所有情况下变换器中的开关都工作于ZVS；②自适应频率模式下的a(0)和p(0)都比固定频率模式下的a(0)和p(0)小得多，这意味着自适应频率模式下变换器的环流损耗将显著减小。

为了便于与计算结果进行比较，根据式（15）对a(0)和p(0)的测试值分别进行归一化处理。图10和图11分别给出了|a(0)_PU|和|p(0)_PU|的测试结果，显然，实验结果分别与图7和图8中的计算结果具有很好的一致性。

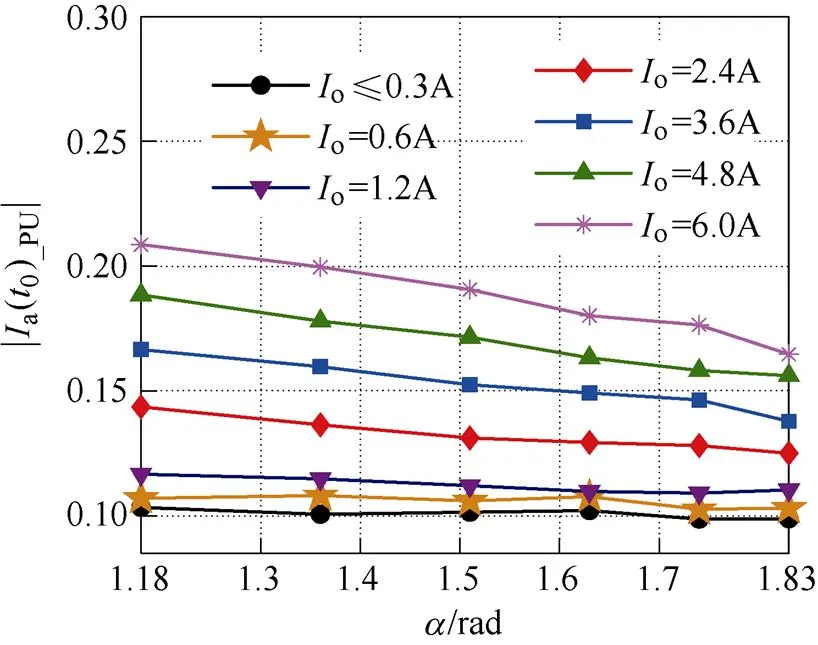
图10 变换器工作于自适应模式时在不同负载电流Io条件下，|Ia(t0)_PU|与a 关系的测试结果

图11 变换器工作于自适应模式时在不同负载电流Io条件下|Ip(t0)_PU|与a 的关系的测试结果

图12给出了输入电压in=300V时变换器的损耗分布。与固定频率模式相比，变换器在自适应频率模式下，开关管损耗、变压器损耗和辅助电路的功率损耗都降低了，这是因为在自适应频率模式下环流损耗减小了（见图6、图8和图11）。

图12 输入电压Vin=300V时的损耗分布

图13给出了本文所提出的变换器的效率测试结果，显然，变换器工作于自适应频率模式下具有更高的效率。当in=200V（=1.18rad）并且o=6A（满载）时，两种工作模式具有相同的效率，但随着输入电压变大或/和负载电流变小，采用自适应频率模式可以获得更高的效率。将图12中的损耗估算结果折合成效率值与图13c中的测试结果比较，计算结果与实测结果具有较好的一致性。

图13 在轻负载条件和重负载条件所提出的变换器的测试效率

带有并联电感辅助支路或LC辅助支路的PSFB变换器[3, 18-20, 26-27]能够有效拓展ZVS范围，减小开关损耗。由于辅助支路引入的损耗小于开关损耗，因此能够提高变换器的效率[18, 26-27]。较之其他类型的解决方案，这种方案在效率上可能不是最佳选择，但具有简单、鲁棒性强与成本低的显著优势。与类似解决方案[3, 18-20, 26-27]相比，本文需要考虑变压器励磁电感的设计，但在以下两个方面具有优势：①辅助电路所用的器件数量最少；②既能实现辅助电流的输入电压自适应，也能实现辅助电流的负载自适应。

5 结论

本文通过在传统隔离型全桥拓扑的基础上增加一个简单LC电路，提出了一种辅助电流随着输入电压和负载变化而自适应变化的ZVS移相全桥变换器，该变换器能够在整个输入电压范围和负载范围内实现ZVS，并具有很小的环流损耗。

由于辅助电流的峰值对开关频率的变化非常敏感，因此能够采用较窄的频率变化对辅助电流进行有效的调节而不会对主电路的设计和控制带来明显的影响。

实验结果验证了本文所建立的数学模型的准确性和设计方法的有效性，为变换器的优化设计和精确控制提供了依据。

[1] Teng J H, Liu B H. Three-stage dead-time adjustment scheme for conversion efficiency enhancement of phase-shift full-bridge converters at light loads[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 1210-1219.

[2] 沙德尚, 李斌, 袁文琦, 等. 基于负载自适应的辅助LC网络宽范围零电压开通的输入串联输出并联移相全桥DC-DC变换器[J]. 中国电机工程学报, 2016, 36(13): 3558-3564, 3374.

Sha Deshang, Li Bin, Yuan Wenqi, et al. Loads adaptive input-series-output-parallel phase shift full bridge derived DC-DC converters with auxiliary LC networks to achieve wide zero voltage switching range[J]. Proceedings of the CSEE, 2016, 36(13): 3558-3564, 3374.

[3] Pahlevaninezhad M, Drobnik J, Jain P K, et al. A load adaptive control approach for a zero-voltage-switching DC-DC converter used for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 920-933.

[4] Shih L, Liu Y, Chiu H. A novel hybrid mode control for a phase-shift full-bridge converter featuring high efficiency over a full-load range[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(3): 2794-2804.

[5] 赵钧, 林弘毅, 孙晓玮, 等. 基于简化状态轨迹的半桥LCC谐振变换器无噪声Burst模式控制策略[J]. 电工技术学报, 2021, 36(20): 4215-4224.

Zhao Jun, Lin Hongyi, Sun Xiaowei, et al. A novel noiseless burst mode control of half-bridge LCC resonant converter based on simplified state traje- ctory[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4215-4224.

[6] 刘晓东, 董保成, 吴慧辉, 等. 基于并联变压器切换的LLC谐振变换器宽范围效率优化控制策略[J]. 电工技术学报, 2020, 35(14): 3018-3029.

Liu Xiaodong, Dong Baocheng, Wu Huihui, et al. Wide range efficiency optimization control strategy for LLC resonant converter based on parallel trans- former switching[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3018-3029.

[7] Sabate J A, Vlatkovic V, Ridley R B, et al. Design considerations for high-voltage high-power full-bridgezero-voltage-switched PWM converter[C]//5th Annual Proceedings on Applied Power Electronics Confer- ence and Exposition, Los Angeles, 1990: 275-284.

[8] Gautam D, Musavi F, Edington M, et al. An auto- motive on-board 3.3kW battery charger for PHEV application[C]//2011 IEEE Vehicle Power and Pro- pulsion Conference, Chicago, 2011: 1-6.

[9] Zhao Lei, Li Fei, Zhuang Zhemin, et al. A dual half-bridge converter with current doubler rectifier[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6398-6406.

[10] Zhao Lei, Luo Zejia, Fan Zhun, et al. A dual half- bridge converter with hybrid rectifier for DC power supply in railway systems[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4579-4587.

[11] Salman Khan, Sha Deshang, Jia Xiangshuai, et al. Resonant LLC DC-DC converter employing fixed switching frequency based on dual-transformer with wide input-voltage range[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 5120-5127.

[12] 李广地, 阮杰, 王昆, 等. 一种混合调制型三路输出DC-DC变换器[J]. 电工技术学报, 2019, 34(22): 4719-4727.

Li Guangdi, Ruan Jie, Wang Kun, et al. A hybrid modulated triple-output DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(22): 4719-4727.

[13] Lee S, Park J W. A new control for synchronous rectifier of phase-shifted full-bridge converter to improve efficiency in light-load condition[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3822-3831.

[14] Kim C E. Optimal dead-time control scheme for extended ZVS range and burst-mode operation of phase-shift full-bridge (PSFB) converter at very light load[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10823-10832.

[15] Cho J G, Baek J W, Jeong C Y, et al. Novel zero- voltage and zero-current-switching full-bridge PWM converter using a simple auxiliary circuit[J]. IEEE Transactions on Industry Applications, 1999, 35(1): 15-20.

[16] Nama J K, Verma A K, Srivastava M, et al. An efficient inductive power transfer topology for electric vehicle battery charging[J]. IEEE Transa- ctions on Industry Applications, 2020, 56(6): 6925- 6936.

[17] Cho J G, Sabaté J A, Lee F C. Novel full bridge zero-voltage-transition PWM DC-DC converter for high application[C]//1994 IEEE Applied Power Elec- tronics Conference and Exposition, Orlando, 1994: 143-149.

[18] Hamada S, Nakaoka M. Analysis and design of a saturable reactor assisted soft-switching full-bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 1994, 9(3): 309-317.

[19] Jain P K, Kang Wen, Soin H, et al. Analysis and design considerations of a load and line independent zero voltage switching full bridge DC-DC converter topology[J]. IEEE Transactions on Power Electronics, 2002, 17(5): 649-657.

[20] Daneshpajooh H, Pahlevaninezhad M, Jain P, et al. An efficient soft switched DC-DC converter for electric vehicles[C]//28th Annual IEEE Applied Power Electronics Conference and Exposition, Long Beach, 2013: 1798-1803.

[21] Kanamarlapudi V R K, Wang B, So P L, et al. Analysis, design, and implementation of an APWM ZVZCS full-bridge DC-DC converter for battery charging in electric vehicles[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6145-6160.

[22] Borage M, Tiwari S, Kotaiah S. A passive auxiliary circuit achieves zero-voltage-switching in full-bridge converter over entire conversion range[J]. IEEE Power Electronics Letters, 2005, 3(4): 141-143.

[23] 陈仲, 汪洋, 李梦南. 一种低环流损耗的宽范围 ZVS移相全桥变换器[J]. 电工技术学报, 2015, 30(22): 71-79.

Chen Zhong, Wang Yang, Li Mengnan. Wide-range zero voltage switching phase-shifted full-bridge converter with low circulation loss[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 71-79.

[24] Zhao Lei, Li Haoyu, Wu Xiao, et al. An improved phase-shifted full-bridge converter with wide-range ZVS and reduced filter requirement[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(3): 2167- 2176.

[25] Zhao Lei, Li Haoyu, Xu Chuanyu, et al. Efficiency improvement of an adaptive-energy-storage full- bridge converter by modifying turns ratio of a coupled inductor[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 948-956.

[26] Safaee A, Jain P, Bakhshai A. A ZVS pulsewidth modulation full-bridge converter with a low-RMS- current resonant auxiliary circuit[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(6): 4031-4047.

[27] Yang Xiaoguang, Li Yuqi, Gao Zheng, et al. Analysis and design of full-bridge converter with a simple passive auxiliary circuit achieving adaptive peak current for ZVS and low circulating current[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 2051-2065.

[28] 刘瑞欣, 王议锋, 韩富强, 等. 应用于宽输入电压范围的两模式切换型软开关谐振直流变换器[J]. 电工技术学报, 2020, 35(22): 4739-4749.

Liu Ruixin, Wang Yifeng, Han Fuqiang, et al. A two-mode soft-switching resonant DC-DC converter for wide input voltage range applications[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(22): 4739-4749.

[29] 孙加祥, 吴红飞, 汤欣喜, 等. 基于整流侧辅助调控的交错并联LLC谐振变换器[J]. 电工技术学报, 2021, 36(10): 2072-2080.

Sun Jiaxiang, Wu Hongfei, Tang Xinxi, et al. Interleaved LLC resonant converter with auxiliary regulation of rectifier[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2072-2080.

[30] 冯兴田, 邵康, 崔晓, 等. 基于多模态切换的宽电压增益LLC谐振变换器控制策略[J]. 电工技术学报, 2020, 35(20): 4350-4360.

Feng Xingtian, Shao Kang, Cui Xiao, et al. Control strategy of wide voltage gain LLC resonant converter based on multi-mode switching[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4350- 4360.

[31] Ayachit A, Corti F, Reatti A, et al. Zero-voltage switching operation of transformer class-e inverter at any coupling coefficient[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1809-1819.

A Load and Input Voltage Adaptive Zero-Voltage-Switching Full-Bridge Converter

1,21,21,23

（1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of Technology Tianjin 300130 China 3. Shanghai Institute of Space Power-Sources Shanghai 200245 China）

This paper presents a zero-voltage-switching (ZVS) full-bridge DC-DC converter operating in a wide input voltage and load range. The proposed converter is derived from the addition of a simple LC auxiliary circuit to the traditional phase-shifted full-bridge (PSFB) converter. The auxiliary current is controlled through a narrow frequency change, and the circulating current loss can be minimized under the ZVS operating conditions. The use of a narrow frequency change can effectively adjust the auxiliary current without significantly affecting the design and control of the main circuit. The steady-state performance of the converter is analyzed in detail; the mathematical model of the converter is established, which can be directly used for the optimized design and precise control of the converter. The experimental results are in good agreement with the analysis results.

Circulating loss, full-bridge converter, load adaptive, input voltage adaptive, resonant circuit, zero-voltage-switching (ZVS)

10.19595/j.cnki.1000-6753.tces.211163

TM46

2021-07-29

2021-10-13

杨晓光 男，1971年生，博士，教授，研究方向为电源及其磁技术。E-mail: xgyang@hebut.edu.cn（通信作者）

王德鑫 男，1996年生，硕士研究生，研究方向为电源新技术。E-mail: EE_wangdexin@163.com

（编辑 陈 诚）