基于自适应尺度变换-双稳态随机共振模型的BPSK信号检测算法
刘 斌, 范翔宇, 张自伟, 张 烨
(1. 国防大学联合作战学院, 北京 100091; 2. 空军哈尔滨飞行学院, 黑龙江 哈尔滨 150088)
0 引 言
二进制相移键控(binary phase shift keying, BPSK)信号已被广泛应用于现有的通信协议之中,如IEEE 802.11a以及第二代数字地面电视广播系统[1],用于保证较差的无线信道的服务质量(quality of service, QoS)。由于实现简单技术成熟,BPSK信号与其调制样式在光学、通信等领域中有都着广泛的应用[2-4]。因此,对BPSK信号的检测技术一直是学术界研究的热点。
学者们致力于相关应用领域的研究并取得了丰硕的成果。文献[5]利用相敏放大器(phase sensitive amplifiers,PSAs)的低噪声放大以提升BPSK信号的功率,有利于信号的检测。文献[6-7]在PSAs的基础上对信号进行相位再生,得到BPSK信号相位维度的信息以提升检测效能。受到电子元件带宽的限制,此类方法只适用于单通道操作。文献[8]对上述方案加以改进,然而依旧受到带宽的影响。文献[9-10]基于应用物理层网络编码(physical-layer network coding,PNC)设计了信号传输系统,其中文献[9]利用PNC的改进算法抑制载波频率偏移所产生的载波间干扰,从而降低了BPSK信号传输的误码率。文献[11-12]利用Cramer-Rao下限(Cramer-Rao lower bound, CRLB)来估计BPSK信号的信噪比(signal to noise ratio, SNR)。文献[13]基于最小误码率准则对信道进行估计,上述方法均为提升系统输出SNR奠定了理论基础,提升BPSK信号的估计准确性。文献[14]理论推导出BPSK信号在干扰条件下的误码率的表达式,通过提升Rice因子的方式改善信号的误码率,但该方法受SNR影响较大。文献[15]指出,BPSK信号在传输过程中,通过保证传输矩阵为满秩即可实现最大的SNR,其满足恒定模数约束,然而该方法需要保证协方差矩阵满秩。文献[16]利用对Godard函数简单修正来改进恒模算法(constant modulus algorithm,CMA)实现对具有相同的速率和相同的载波频率的BPSK信号的盲分离,然而该方法需要知道接收器的BPSK源频率偏移。文献[17]利用正交频分复用的BPSK(BPSK-orthogonal frequency division multiplexing,BPSK-OFDM)信号的在时变信道中实值特性来精确设计,该方法具有更准确的检测能力和更低的计算复杂度,然而该方法需要知道均衡矩阵结构中BPSK-OFDM信号的先验信息,在实际中是难以实时得到。文献[18]通过增加子带阶数增强系统性能,来降低BPSK信号在多谐波干扰条件下的误码率,该方法性能受系统参数影响较大。文献[19]采用自适应窗口交叉Wigner-Ville分布方法来检测BPSK信号,其结果在特定情况下接近Cramer-Rao下限。然而不同应用背景条件下核函数的选取与参数设置,以及时频分辨率彼此之间的矛盾,制约着时频分析方法性能。文献[20]利用压缩感知理论以远小于奈奎斯特采样率的频率对BPSK信号进行采样,降低对存储资源的需求,提升了处理速度,削弱了迭代干扰对BPSK信号检测的影响。然而,压缩感知理论要求信号自身具有稀疏性,限制了该方法在实际中的应用。文献[21]利用循环自相关将信号转换到循环平稳维度上,提取信号特征以实现对BPSK信号的检测,但在非高斯噪声背景下,方法的效能下降。
上述方案在其设定的背景下具有良好的性能,然而3个共性的问题制约上述方法性能的进一步提升:一是在抑制噪声的同时,信号的能量也被削减甚至丢失了部分信息,只是相较于噪声被削弱的程度,信号被削弱的程度较小。在低SNR条件下,很容易在处理过后混合信号SNR依旧不理想,从而影响后续的信号检测。二是信号处理系统自身也是噪声源,在抑制背景噪声的过程中,系统内部产生的噪声,在处理过程中出现的高次谐波、镜像信号等也影响着信号的检测。三是随着噪声强度的增加,上述系统效能恶化明显,检测效能大幅衰落。这3个问题产生的根源是学者们认为噪声始终不利于信号的检测。鉴于此,提升弱信号检测性能的方法,主要通过降低噪声的影响以及改善信号特性两方面进行。在这种思想下,提出的方法始终会受到上述3个问题的限制。
在传统的线性理论中,噪声对于信号而言是有害的。而在非线性理论的双稳态随机共振(bistable stochastic resonance, BSR)系统中,当系统、信号和噪声三者达到某种匹配关系时,系统产生随机共振,其效果在宏观上看是噪声的能量向弱信号移动,即信号自身的能量不仅没有损失,反而得到增强,从而提升了信号的SNR,更有益于信号检测。现有的方法分为调节噪声特性[22-23]与系统参数[24-25]两种。而在实际中,噪声很难设定或调节,为此,论文借鉴随机共振理论,将其运用到BPSK信号检测中,并基于Neyman-Pearson准则设计非线性检测器,对系统的输出信号进行进一步的检测。
论文结构安排如下,首先第1节简要介绍BPSK、BSR以及Neyman-Pearson准则,然后第2节利用尺度变换改进BSR并构建信号检测的完备流程,并在第3、4节中采用基于Neyman-Pearson准则设计非线性检测器,并推导出系统的输出SNR和BER,最后利用仿真证明所提方法的有效性,并与主流方法对比突出算法的优势。
1 相关理论
1.1 BPSK信号模型
对于长距离通信和无线传输,通常使用带通调制,也称载波调制,通过一串数字符号用来改变高频正弦载波的参数。正弦信号有3个参数:幅度、频率和相位。所以在带通调制中有3种基本的调制方式:幅度调制、频率调制和相位调制。图1给出了3种基本的二进制载波调制,分别是振幅键控(amplitude shift keying, ASK)、频移键控(frequency shift keying, FSK)和相移键控(phase shift keying, PSK)。在ASK调制中,当发送的符号是“1”时调制器输出载波,当发送的符号是“0”时没有输出,所以这种调制又称为通断键控(on off keying, OOK)。在一般的ASK调制方案中,发送符号为“0”时的载波幅度也不一定是“0”。在FSK调制中,当发送的符号是“1”时输出一个较高频率的载波,当发送的符号是“0”时输出一个较低频率的载波,或者反过来也可以。在PSK调制中,当发送的符号是“1”时输出初始相位为“0”的载波,当发送的符号是“0”时输出初始相位为180的载波。
相移键控是一种通过改变载波相位进行数据传输的数字调制方案。通过特定的相位表示由比特形成的符号。其中,BPSK只有两个相位表示数据比特“0”和“1”。BPSK信号通常定义为
(1)
式中:A为信号的幅度;fc为载波频率;θ0和θ1分别为0比特和1比特的相位偏移。
BPSK复合调制信号由于具有大时宽带宽积、高分辨率和低截获概率的特性,在信号处理领域引起了学者们的广泛关注[26-27]。典型的叠加高斯白噪声的信号模型如下所示:
x(n)=Aexp[j(2πfΔtn+θ(n))]·rect(n)+ω(n)
(2)
式中:rect(·)为矩形方波;f为BPSK信号的频率编码;Δt为采样间隔;θ(n)为相位编码;ω(n)为服从标准正态分布的高斯白噪声序列。BPSK信号调制方式主要体现在相位函数上,其中
θ(n)=π·d(n)
(3)
1.2 双稳态随机共振
具有双势阱性质的郎之万方程是最为经典的双稳态非线性系统,该系统模型可以表示为
(4)
式中:U(x)为双稳态随机共振系统的势函数;系统的输入信号为s(t)设系统背景是均值为0、方差为D、幅度为N(t)的高斯白噪声(white Gaussian noise, WGN),a,b为系统的结构参数且均为大于0的实数;x为系统的输出变量,用于描述在系统的影响下,信号和噪声发生共振后系统的输出,且统计均值及自相关函数为
(5)
式中:δ(t)为冲激函数。
当D=0时,假设只有在信号输入时才有噪声,系统在势阱的阱底具有两个稳态。两个阱底之间有一个势垒ΔU,只有越过势垒系统才能在两个阱底之间产生共振,势垒的高度为
(6)
为了越过该势垒,输入信号的幅度需要超过阈值Ac。令式(4)中势函数的极点与拐点重合,即
(7)
得到阈值Ac的表达式为
(8)
将系统的输出看作在势函数曲线上运动的质点。当信号输入系统后,势阱在信号的调制驱动下,按信号的频率发生周期性的倾斜变化,如图2和图3所示。
当输入信号的幅度小于阈值Ac时,质点不能从一个势阱跃迁到另外一个势阱,此时只能在这两个势阱之间进行周期运动。只有当输入信号的幅度大于阈值Ac时,质点才能从一个势阱跃迁至另外一个势阱,然而由于需要向系统中添加噪声,此时则会因为信号与噪声的相互作用,导致势阱的倾斜程度将会逐渐变大,最终同样能够使质点从一个势阱跃迁到另外一个势阱。此外,对于添加的噪声而言,当其为最佳的噪声强度时,此时能够保证输出的SNR达到最大,有利于后续的信号检测。而在此强度上继续增加则会导致质点的运动会失去规律性,使得系统输出SNR明显下降。
但这里对信号和噪声是有相应要求的。对于信号来说,由于双稳态随机共振系统存在如式(6) 所示的势垒,信号能量只有在超过势垒时才能激发随机共振,即要求信号的幅值超过式(8)中的阈值,否则系统不会产生随机共振效应。从前文叙述中可知,虽然向随机共振系统中添加噪声能够有效增强信号能量,但是所添加的噪音强度并不是越高越好,一旦信号SNR低于可检测SNR下界,任何处理方法都无法实现对于信号的检测。因此,对所添加噪声的要求是不能使SNR低于可检测SNR下界。
双稳态随机共振可以将噪声的能量转换为信号的能量,从而不仅保留了原始信号的信息同时更有利于对其实现检测。然而经典的双稳态随机共振只能应用于强度小、频段低的周期信号,上述3个条件一旦缺失其一就会导致系统不能匹配工作。这样的条件严重的限制了随机共振理论的应用。而在实际应用中,信号强度的大小、频段的高低都只是背景中的相对值,同时基于傅里叶变换的思想,非周期信号也可以看成周期无限大的信号。因此,有可能将双稳态随机共振理论的适用范围进一步拓展,论文也将利用尺度变换的思想来拓展双稳态随机共振理论的适用性。
1.3 Neyman-Pearson准则
雷达信号检测本质上是将输入信号x(t)进行处理后与检测门限做比较,判断目标是否存在。其中有两种情况,一是包含信号和噪声,即x(t)=s(t)+n(t),此时称为H1假设;二是仅含有噪声,即x(t)=n(t),称为H0假设,表示为
(9)
如图4所示,二元检测的过程也是划分观测空间D的问题,即根据判决门限将D划分为判决域D1(有信号)和判决域D2(无信号)两个子空间,且D=D1∪D0,D1∩D0=∅。H0假设成立的条件是观测量(x|H1)或(x|H0)处于D0子空间;同样,H1假设成立的条件是观测量处于D1子空间。
根据检测判决情况,可将结果表示为
(10)
式中:Pd称为检测概率;Pn称为正确不发现概率;Pfa称为虚警概率;Pm称为漏警概率。P(H1|H1)代表H1假设下判决目标存在的概率,其他表达式类似。
设H1出现的先验概率为P(H1),H0出现的先验概率为P(H0),则P(H1)=1-P(H0)。若观测信号x(t)的两种概率密度函数分别为p(x|H1)和p(x|H0),检测门限为VT,则有:
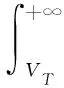
(11)
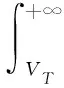
(12)
检测门限VT取决于采用的检测准则,在雷达信号检测中最常用的是Neyman-Pearson准则,即在虚警概率一定的情况下,使检测概率最大化。用数学表示如下:在Pfa=α(α为常数)的约束条件下,使得Pd最大化。
2 基于变尺度随机共振的信号处理流程
2.1 尺度变换模型与证明
随机共振系统的理论分析和定量推导是以绝热近似理论和线性响应理论为基础的,上述理论均要求待测信号在频率极低且幅度极小的双重限定条件下进行。因此,经典的随机共振理论只能处理不超过几个赫兹的小振幅低频信号[28-30]。然而在实际的科学研究与工程应用中,信号的中心频率较高且频带较宽。因此,为提高所提算法的适用性,本节引入双稳态系统模型的归一化尺度变化,并在结合推导证明的基础上,论证可通过调整参数拓展BSR的适用范围。
本节对式(4)进行变量替换,即实现尺度变换。令
(13)
τ=at
(14)
将式(4)和式(5)代入式(2)中,整理可得
(15)
令
(16)
则式(16)满足
(17)
将式(17)代入式(15)中可得
(18)
将式(18)整理可得
(19)
式(19)是式(4)的归一化形式,即两者是等价关系,此时的信号频率为原始信号频率的1/a。因此,对于高频信号可以通过选择加大系统参数a,同时提高信号的采样频率,即可使待检测信号归一化为等效的低频信号,进而可以利用随机共振理论进行分析与求解。且由于信号与噪声均乘相同的比例因子,因此对于原始系统而言,其SNR并没有改变。
2.2 算法流程
第2.1节论述了利用尺度变换方法拓展随机共振的可行性,本节构建基于双稳态系统的信号处理流程。其流程如图5所示。
该算法步骤可归纳总结为如下6个步骤:
步骤 1根据郎之万方程构建BSR系统,初始化BSR系统的结构参数a0=b0=1,选取信号振幅A0=0.5,频率f0=0.5,噪声标准偏差σ0=0。
步骤 2估计待检测BPSK信号频率fBPSK为f1量级,设置采样频率fs为f1量级的100倍,即使待检测信号的频率f1远小于采样频率fs,并保证尺度变换后信号转换为等价的低频区。
步骤 3利用a1≐a0(f1/f0),并令b1≐a1,得到尺度变换后的双稳态系统参数a1、b1,从而构建随机共振系统。其中,≐表示约等为此量级。
步骤 4对待检测的混合信号进行采样,并计算信号的均方根(root mean square, RMS)值σ1。由于本节设定为低SNR条件,即设定混合信号的均方根值与噪声的均方根值几乎相同,利用K=σ0/σ1,可以得到比例因子K。
步骤 5将待检测混合信号乘以比例因子K,并将结果输入到随机共振系统中,然后将共振系统输出的结果输入信号检测系统,得到系统的误码率,若误码率未达到理想值,则以此微调a1并返回步骤3进行重新计算,以降低结果的误码率,若达到理想值则进行步骤6。
步骤 6调整参数使误码率最低,此时信号处理结果最为理想。输出系统的检测波形与对应的误码率即可实现对于BPSK信号的检测。关于信号检测与误码率的计算部分,将会在后文进行详细论述。
3 基于Neyman-Pearson准则的非线性阈值系统检测流程
为了进一步有效地从噪声中提取弱信号,本节基于Neyman-Pearson准则设计了信号检测器,以实现信号处理流程中的信号检测部分,即为图5中的信号检测部分。
由于通过BSR系统的BPSK信号与噪声的混合信号会受到非线性作用的影响,导致噪声的概率密度函数发生变化。本节设定在较高的SNR条件下进行仿真实验,输入信号为0.03 Hz,SNR为-10 dB,所得结果如图6所示。
通过对比图6中的结果可以看出,在经过随机共振系统的非线性处理后,噪声的功率向着信号所在频点方向聚集,即通过随机共振系统后,噪声已经不再服从正态分布。为此,利用Neyman-Pearson准则设计非线性阈值系统(nonlinear threshold system, NTS),其函数模型如图7所示。
其表达式如下:
(20)
式中:T和P是两个常数,其值在后文给出。由于本节要检测BPSK信号是否存在,对其离散化处理可得
(21)
式中:N为采样点数。
由于BPSK信号每个码元会持续一段时间,且采样频率远高于信号的频率,即当BPSK信号存在时,系统会连续采集到s1(k)与噪声或s2(k)与噪声的混合信号,本节将以此作为信号检测的依据。
如果存在信号时,系统接收到s1(k)与s2(k)的概率均为0.5。先假设系统接收到的是s1(k),噪声为n(k),则信号的有无可用二元假设检验表示,即
(22)
由于高斯白噪声通过BSR系统时,其概率密度函数会发生变化,此外,由于非线性系统的处理机制难以通过理论分析得到,且非线性系统具有初值敏感性,故本节不推导高斯白噪声通过双稳态系统后的概率密度函数。为设计检测器,且保证算法的普适性,假设噪声服从广义高斯噪声,其概率密度函数如下:
(23)
式中:μn、σn分别为噪声的均值和方差;p>0、β>0;Γ(x)和β的表达式为
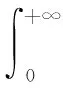
(24)
(25)
式中:p的值表示噪声类型,不同的p值对应于不同的噪声概率密度函数。根据BSR的输出结果,分析噪声特性并对其进行参数化建模,根据所得结果来确定近似的噪声分布模型,从而确定p的取值。
本节假设T=1、P=-1,则此时阈值系统可以看作为一个符号函数,可表示为
(26)
首先,计算输出信号y的均值,可以表示为
E[y]=P(y=1)-P(y=-1)=P(s1+n≥θ)-P(s1+n<θ)=1-2Fn(θ-s1)
(27)
式中:
(28)
式中:fn(u)是式(23)中广义高斯噪声的概率密度函数。
计算输出信号y的方差为
E[y2]=(1)2P(y=1)+(-1)2P(y=-1)=1
(29)

(30)
得到非线性阈值系统的检验统计量为
(31)
在H0与H1假设条件下,检验统计量具有不同的均值和标准差,分别设为μ0、σ0、μ1、σ1。根据检验统计量的性质,其值分别为
μ0=1-2Fn(θ)
(32)
μ1=1-2Fn(θ-s1)
(33)
(34)
(35)
由于BPSK信号的第一个码元会存在一段时间,且系统的采样率足够高,即对信号的采样点数足够大,根据中心极限定理,在上述两种假设条件下,检验统计量均服从高斯分布,其概率密度函数为
(36)
(37)
为提升检测系统对于信号处理的效能,本节采用Neyman-Pearson准则来设计检测器,以保证有用的信息尽可能多地进入系统,同时也避免了过多的虚假数据进入检测器,从而影响系统的工作效率。即当虚警概率PF恒定时,使检测概率PD最大。两者表示为
(38)
(39)
由于Neyman-Pearson准则是在设定虚警概率PF后,对式(38)进行变下限定积分,从而得到门限值α的。本节假设PF已设定,将式(36)代入式(38)中,可得
(40)
对式(40)进行变量代换,令
(41)
则式(27)可表示为
(42)
式(42)没有理论解,而在实际应用中,可结合标准正态函数的分布表,即下式所对应的函数值,进行辅助计算:
(43)
则虚警概率可表示为
(44)
即当虚警概率设定后,标准正态函数的函数值可以确定,则μ0、σ0可通过计算得到,最终通过查表和简单计算即可以得到门限值α,进而可以得到检测概率为
(45)
经过随机共振系统处理后的混合信号检测流程即如图8所示。利用Neyman-Pearson准则,能够在没有先验信息条件下,进一步对BPSK信号的检测能力。由于上述的推导是基于接收到的信号为“+1”进行的,通过上述计算可以得到检测概率PD。然而,在实际应用中BPSK信号的第一个码元可正可负。为此本节采用两套相同检测系统,第一套正常处理,将信号倒转输入到第二套检测系统,即将s(t)变成-s(t),双系统同时工作,得到第二套检测系统的检测概率PDv,对比PD与PDv,两者大小区别会很大,取较大值为此时的信号检测概率,同时也可以确定信号为正或为负。即第一套系统只检测正信号,第二套检测负信号,将两者检测出的信号序列相加,即可得到BPSK信号的完整序列。
4 算法性能分析
4.1 检测性能分析
为定量分析算法性能,本节将对所提算法对于信号检测能力的提升进行量化描述。
由BPSK信号的表达式可以看出,在每个码元之间信号为正弦波,此时双稳态系统的单边输出功率谱密度(power spectral density, PSD)函数可以表示为
(46)
式中:A是BPSK信号的幅度;D是WGN的噪声强度;ωc=2πfc是BPSK信号的角频率,fc是信号的调制载波频率。在绝热近似的条件下,要确保双稳态系统能够产生随机共振,BPSK信号调制频率应满足:
(47)
则输出信号功率Ps可以表示为
(48)
噪声功率Pn可表示为
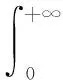
(49)
则通过整理可得,输出信号的信噪比SNRout可以表示为
(50)
输入信号的SNRin为
(51)
则双系统信号输入前后的SNR增益为
(52)
为保证G大于1,式(52)应满足:
0 (53) 求解上述关于D的一元二次不等式组,可得 (54) 即当原始噪声强度满足上述条件时,系统的输出SNR会提升。 为研究噪声与系统参数之间的关系,设 (55) 由式(55)可以看出,系统增益与参数a呈正相关。为保证增益大于1,参数a应满足: (56) 求解可得 (57) 由于系统增益是关于a的单调递增函数,因此,当a的取值接近上限时,系统的增益会达到最大。 从式(52)中也可以看出,随着a的增大SNR也在逐步提升,此外本节所提出的尺度放缩也要求a尽可能大,即增大a既可以拓展随机共振的适用性,同时也可以提升系统的增益,这也是所提的尺度放缩方法的一个重要优势。 通过双稳态系统后信号的SNR得以提升,为评估检测器的性能,本节利用误码率Pe作为评判指标,同时也作为信号处理系统中的反馈量。其表达式如下: Pe=P0P(0|1)+P1P(1|0) (58) 式中:P1和P0分别表示有无码元的概率。在Neyman-Pearson准则的条件下,本节将BPSK信号转换为两组二元检测,即P(0|1)表示为漏警概率,P(1|0)为虚警概率,有: (59) 结合第3节的推导结果,检测器的误码率可以表示为 (60) 由式(60)可得,虚警概率PF设置的越高,检测门限α越低,检测概率PD越高,漏警概率越低,反之亦然。因此,式(60)表明,误码率会随着人为设定虚警概率的降低而呈现出先降低后上升的过程,即存在一个理想的虚警概率PFopt,使系统的误码率最低。同时也可从Φ函数看出,误码率Pe与通过检测器前的噪声强度相关,而经过双稳态随机共振系统的处理,输出信号的SNR得到了提升,从而降低了检测信号的误码率。上述过程即为信号处理流程中误码率计算的部分,根据误码率的大小调整系统参数,以实现最优检测。 在步骤3中,a1近似为a0的f1/f0倍,虽然可以实现比例缩放,但并不需要实现最优的参数匹配。因此,应该调整a1与a0的比例。式(60)表明,系统的误码率与信号的传输概率P0和P1以及所设定的虚警率PF有关。同时,根据Neyman-Pearson准则,当设置了接收器的虚警概率时,其检测概率PD也可以根据观测者操作特征(receiver operating characteristic, ROC)曲线来确定。 为了实现a1的最优匹配,可以在对信号进行检测前将接收机的参数进行调整。首先,设置P0、P1和PF,用已知的编码方法构建与待检测信号的幅度和频率相似的BPSK信号,然后将其输入到强噪声检测系统中。根据信号和噪声参数计算PD,进而得到式(60)的结果,即理想条件下的误码率Peopt,并计算系统在第q次调整后的实际误码率为Per(q),算得这两个值之间的误差为err(q)。根据所得误差对a1和a0的比值进行调整,并设计控制律如下所示: (61) 初始条件为 (62) 式(61)是比例控制的经典方法,技术成熟且易于实现。当误差为0时,调整系统参数并记录调整次数Q,这里有q∈[1,Q]。在确保在此系统参数的条件下对参数a1进行调整,可有效降低误检测率。 算法流程表明,所提算法首先通过双稳态随机共振系统对混合噪声信号进行处理,然后根据Neyman-Pearson准则对输出信号进行检测,再根据误检测率对双稳态系统的参数进行调整,直至获得最低的误码率。因此,有必要对随机共振和检测算法的叠加计算量进行分析,然后进行Q次迭代以获得最优解的次数,即为算法的复杂度。 首先,分析经过尺度变换的双稳态随机共振系统。第一步是尺度变换,即式(13)和式(14),将信号的尺度和频率变为原始值的1/a,该算法的复杂度为O(n)。然后将尺度变化的结果输入到双稳态随机共振系统中即式(4),该步骤的计算量主要来源于bx3,其复杂度为O(n3)。因此,该双稳态随机共振系统的算法复杂度为O(n+n3),即O(n3)。 其次,对信号检测进行分析。在确定概率密度函数中的广义噪声分布后,根据双稳态随机共振系统的输出结果选择p的值,进而实现对噪声的近似描述,则算法复杂度为O(1),然后计算参数μ0、σ0、μ1、σ1的值。式(32)~式(35)表明该σ算法的复杂度比μ更高,因此,我们只研究σ的算法复杂度。Fn由式(28)进行积分计算得到的,被积函数和积分的界是已知的,且被积函数是一个典型的分布函数,因此,可以通过查表来确定Fn的值,其计算复杂度为O(n)。对于σ复杂度的计算可以通过式(34)和式(35)得到,则计算σ的复杂度为O(n3)。接下来,通过设定的PF推导出阈值α。同样,式(42)表明被积函数和积分的界是已知的,且被积函数满足典型的高斯分布,则阈值α可以通过查表和简单的计算得到,其计算复杂度为O(n2)。最后,对检验统计量进行分析。根据式(31),将检验统计量为输出信号的平均值与阈值进行比较,这两部分的算法复杂度为O(n)。综上所述,信号检测部分的算法复杂度为O(1+n+n3+n2+n),即O(n3)。 最后,根据图5中的算法流程,除双稳态随机共振和信号检测外,其余大部分都是简单的四项操作和赋值,只有计算环境中的噪声方差算法的复杂度为O(n2)。因此,系统的整体算法复杂度为O[Q(n3+n3+n2)],即O(2Qn3)。因此所提的非线性检测算法与大多数信号检测算法复杂度相近,并且能够显著提高弱信号的检测能力,具有较好的性能。 尺度变换的可行性已在前文进行过推导论述,为验证其可行性,本节对其进行仿真实验。这里利用典型的BPSK信号,对尺度变换方法进行仿真验证。 系统的采样频率为600 kHz,系统参数a=b=107,BPSK信号的载波频率为200 kHz,基带频率20 kHz,初始码元任取,初始相位随机,+1、-1码元随机等概率随机变换,噪声与信号强度相同。仿真环境为I7-4960,主频2.60 GHz,16 G内存,基于Matlab 2014a为平台进行仿真实验。将BPSK信号通过上述双稳态系统,得到前后的波形对比如图9所示。 图9中由上至下依次为调制后的BPSK信号、与等强度噪声混合的双稳态系统输入信号以及双稳态的输出信号。通过观察图9可以直观地看出,上述设定的参数可以使系统产生随机共振,即通过实验验证,本节的尺度放缩方法具有可行性。将上述混合信号与输出信号进行快速傅里叶变换分析其频谱,如图10所示。对比两图可得,信号在其频点上的强度明显增强,约为原始信号强度的11倍,输出信号的SNR得到明显提升,有利于信号的检测。且从图10中的第一幅图可以看出,原始噪声为WGN,以一定强度均匀分布在整个频段内,而经过随机共振系统处理过后,其分布明显朝向信号频点聚集,这也验证了在经过变尺度随机共振系统后,噪声的分布改变,不再服从正态分布。为此,需要研究与设计非WGN背景下检测器,对双稳态随机共振的输出信号进行进一步的检测。 为保证随机共振的效果,本实验设定接收信号采样点数足够大,根据中心极限定理,检验统计量服从近似的高斯分布。系统参数和仿真环境与第5.1节仿真条件几乎相同,SNR为-10 dB,虚警概率设为0.01,令广义高斯白噪声参数p=1,即假设噪声经过BSR系统后服从拉普拉斯噪声分布。设定BPSK信号的时间长度为0.1 s,且在该段时间内进行1 000次幅值转换,将其通过第5.1节设定好参数的双稳态系统,将系统输出信号通过非线性检测器,解调双稳态系统输出信号与检测器输出信号。为易于观察,取0.01 s内的波形,如图11所示。通过对比两条曲线可得,双稳态系统能够有效提升信号的能量,信号特性进一步得到了凸显,有利于非线性检测器进行后续检测。将输出信号通过非线性检测器,得到检测后的BPSK信号波形。 为进一步评估检测器输出结果的正确性与计算系统的误码率,这里作出原始纯净信号与检波器输出信号之间的关系图,如图12所示。 对比上述两组点,可以看出在第28次信号调制时,系统没有检测成功,其余99次全部实现了正确检测。在整段1 000次调制的序列中,失败检测了6次,其误码率较低。将上述流程进行100次蒙特卡罗仿真实验,得到检测系统的平均误码率为0.007 6。可见,在-10 dB及拉普拉斯噪声背景条件下,所提算法具有良好的检测性能。 为进一步衡量所提算法性能并体现算法优势,在低SNR条件下,调整p的参数值,并将所设计的检测器与最佳线性检测器(best linear detection, BLD)进行对比,仿真环境与参数值设定不变,仿真SNR为[-30, 0] dB,以3 dB为步进,所得仿真结果如图13所示。可以看出,所提的基于Neyman-Pearson准则设计的非线性检测器在低SNR条件下具有良好的检测性能,且随着SNR的提升检测效能也明显提升。同时,在多数情况下,该检测器性能优于最佳线性检测算法。当p=2时,此时噪声为WGN,BLD对WGN背景下的检测性能最优,且随着p值的变化,所设计的检测器性能优势逐步显现,误码率的下降更为明显。 本文我们将所提算法与文献[31]算法进行了比较,采用与文献[31]中图9相同的仿真参数,将虚警率设为0.05,进行200次蒙特卡罗实验,并对仿真结果进行平均计算,则所提算法与其对比结果如图14所示。横轴为输入信号的SNR,纵轴是输出信号的信干噪比(signal to interference plus noise ratio, SINR)。 图中Rp1、Rp2为文献[31]所构建发射波形的协方差矩阵,该矩阵的形式影响着信号检测能力,其对应的形式如下: (63) (64) 式中:Mt是发射端天线的个数。 可以看出,与文献[31]所提算法相比,采用所提算法可获得更高的SNR。这是因为在低SNR的情况下,所提算法可以通过非线性作用将噪声能量转化为信号能量。因此,所提算法具有比文献[31]算法更好的检测性能。 由于参数调整算法(parameter adjusted algorithm, PAA)的非线性特性,其检测性能与SNR呈线性相关,很难得到具体的解析表达式,这是与文献[31]所用方法的主要不同,但这种算法的检测效率却有显著的提升。然而,从图13可以看出,随着SNR的提高,PAA的检测能力的提升是要慢于其他两种方法的,即使随着SNR的提高,所提算法的检测性能也几乎被其他两种方法所超越。这是因为PAA算法的效率与噪声强度相关,噪声能量降低,检测效率自然也就越低。换句话说,在高SNR条件下,PAA类似的检测性能与主流方法相似甚至更差,然而,在低SNR条件下,这种算法的检测性能显然是比主流方法更好。因此,该方法更适合于弱信号的检测。 为更具有针对性地比较论文所提算法性能,在此对于同样基于随机共振优化的检测算法进行对比,即与文献[32]中的检测算法进行对比,仿真参数的设置与文献[32]中图6仿真条件一致,并设虚警概率为0.1,同样进行200次蒙特卡罗实验并对结果取平均值,其对比结果如图15所示。 由以上对比可以看出,参数调整算法的检测性能虽然略优于改进的能量检测(improved energy detection, IED),同样也优于经典的能量检测(energy detection, ED),但结果上并没有明显的改善。这是因为文献[32]中所提的IED方法需要知道待测信号的参数,然后在随机共振系统中设置参数a和b。所提方法不需要知道待测信号的所有参数,只需要估计信号的频带即可实现信号检测,减少了对先验信息的依赖性,放宽了适用条件。因此,所提方法具有更高的适用性。 此外,当先验信息少于IED方法时,所提算法的检测结果略优于IED方法的另一个原因是,IED方法致力于在高于SNR下界的情况下取得良好的效果,且该算法在SNR低于SNR下界情况其相应的参数调整较为困难。因此,在实际应用中适用范围相对较窄。提出的算法以误码率作为反馈量,根据BPSK信号的参数特征自适应地调整系统参数,并进行参数的动态匹配,从而更好地实现信号的检测。因此,尽管先验信息少于IED方法的信息,但是检测结果可以优于IED方法。 综上,论文所构建的信号处理与检测流程可以在低SNR条件下对BPSK信号实现良好的检测与解调,使得在强噪声背景下的弱信号检测性能明显提升。 (1) 利用BSR系统构建了一套基于尺度变换的BSR模型,提升了对BPSK信号的检测性能,并基于Neyman-Pearson准则构建了非线性信号检测器。将两者结合,构建了一套完整的信号检测流程,实现了在强噪声与无先验信息条件下对弱BPSK信号的检测。 (2) 针对经典的BSR系统只能处理低频段、小幅度周期信号的局限性,本章借鉴尺度变换的思想,将随机共振模型进行改进,拓展其适用范围,通过理论推导与实验验证证明了所提方法的有效性。 (3) 在强噪声背景下对BPSK信号进行检测,首先要确定信号的有无,然而由于针对BPSK信号的先验知识有限,同时在经过随机共振系统后,噪声的概率密度函数发生改变。为此,基于Neyman-Pearson准则设计非线性检测器,并在广义高斯噪声的背景下,给出了检测器的构建及参数确定的完备流程,实现了在不同噪声背景下相应检测器的设计。 (4) 通过理论分析与公式推导,对所提出的系统算法性能进行定量分析,此外,基于算法性能的表达式构建反馈系统,使检测性能达到最优。所提算法不仅适用于BPSK信号,还可应用于其他通信、光学甚至故障信号等,为后续的信号检测理论与实际工程应用提供了良好的借鉴。 所提方法由于基于二项极化的检测方式,因此对于正交相移等多键控的信号检测性能,会随着键的增多而逐步降低,这也是后续的研究方向,将论文方法进行修改与完善,推广到不同键控的信号。4.2 误码率与系统参数优化匹配分析
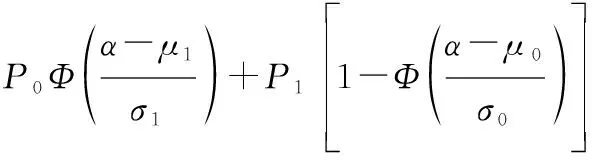
4.3 算法复杂度分析
5 仿真验证
5.1 尺度变换模型
5.2 BPSK信号检测分析
5.3 算法性能对比
6 结 论

