BOUNDEDNESS AND ASYMPTOTIC STABILITY IN A PREDATOR-PREY CHEMOTAXIS SYSTEM WITH INDIRECT PURSUIT-EVASION DYNAMICS*

Shuyan QIU (邱蜀燕)

School of Sciences，Southwest Petroleum University，Chengdu 610500，China

E-mail:shuyanqiu0701@126.com

Chunlai MU (穆春来)

College of Mathematics and Statistics，Chongqing University，Chongqing 401331，China

E-mail:clmu2005@163.com

Hong YI (易红)

School of Mathematics and Statistics，Chongqing Technology and Business University，Chongqing 400067，China

E-mail:honghongyi1992@126.com

Abstract This work explores the predator-prey chemotaxis system with two chemicals in an arbitrary smooth bounded domain Ω⊂Rn under homogeneous Neumann boundary conditions.The parameters in the system are positive.We first prove that if n≤3，the corresponding initial-boundary value problem admits a unique global bounded classical solution，under the assumption that χ，ξ，μi，ai，αi and βi(i=1，2) satisfy some suitable conditions.Subsequently，we also analyse the asymptotic behavior of solutions to the above system and show that · when a1＜1 and both are sufficiently large，the global solution (u，v，w，z) of this system exponentially converges to as t→∞;· when a1＞1 and is sufficiently large，the global bounded classical solution (u，v，w，z) of this system exponentially converges to as t→∞;·when a1=1 and is sufficiently large，the global bounded classical solution (u，v，w，z) of this system polynomially converges to (0，，1，0) as t→∞.

Key words Chemotaxis;predator-prey;boundedness;stabilization

1 Introduction

Chemotaxis，the sustained migration of cells in the direction of an increasing concentration of chemoattractant or decreasing concentration of chemorepellent，has been a significant mechanism in terms of accounting for various biological phenomena (for instance，the aggregation of bacteria，cancer invasion，wound healing，the migration of immune cell)[9，13，26–28].In this work，we will focus on the analysis of solutions to the predator-prey chemotaxis model with two signals;this is a mixed quasi-monotonic system for reaction functions as well as a combination of chemoattraction and chemorepulsion.More specifically，the predator-prey chemotaxis model with indirect pursuit-evasion dynamics reads as

where Ω⊂Rn(n≥1) is a bounded domain with a smooth boundary，andrepresents the derivative with respect to the outer normal of∂Ω.The parametersχ，ξ，μi，ai，αiandβi(i=1，2) are positive.This model describes the spatio-temporal evolution of two populations in which individuals move according to random diffusion，and in which chemotactically directed motion leads to an interaction in a circular manner.Hereu(x，t) denotes the density of prey populations，which move away from the higher concentration ofv(x，t)，the latter being produced by a second species (predator)，the density of which is mathematically represented byw(x，t).The individuals of this second population themselves adapt their movement along the concentration gradients of a second signal，with densityz(x，t)，secreted by the first species (prey).The kinetic terms of the first and the third equations model a predator-prey interaction.The size ofαiandβi(i=1，2) describe the decay and production of the chemical substance，respectively.For more details on the physical background，we refer the reader to[2]and the references therein.

Well-known as the Keller-Segel model，the prototype of the attractive chemotaxis system，in its general form，is given by

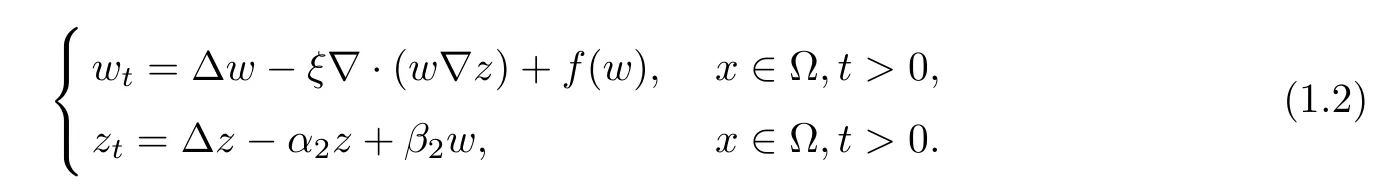
Over the past four decades，a vast amount of mathematical analysis has focused on things such as global boundedness，stabilization，blowup，traveling waves，pattern formations，critical mass phenomenon and critical sensitivity exponents based on the existence of a Lyapunov functional (see e.g.[10，15，31，35–39]).

Another delicate chemorepulsion system reads as

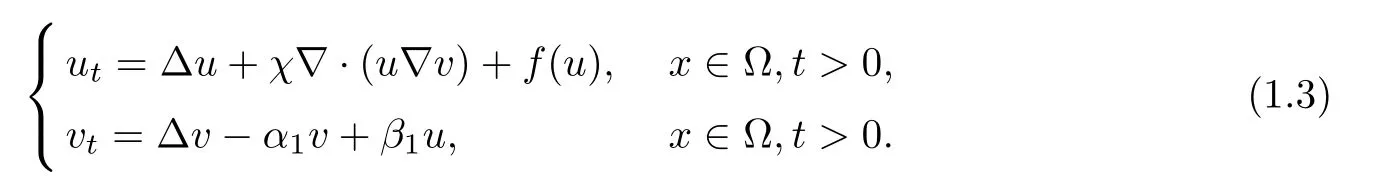
Questions concerning the global existence of classical solutions in two dimensions and weak solutions in three and four dimensions have been investigated for this system[7].In addition，Tao[29]showed the global existence and asymptotic behavior of solutions to (1.3) with nonlinear chemosensitivity in a higher-dimensional space.

After the pioneering works above，a two-species chemotaxis model with one chemical，which is a generalized problem of the KS model，

with coefficientsa1，α，μi，βi(i=1，2)＞0 andχ，ξ，a2∈R，was proposed by Tello-Winkler[32]and was extensively investigated by many authors[3，16，19–21，23，42，44].As with model (1.4) withχ，ξ，a2＞0，it is known that sufficiently largeμ1andμ2ensure the global existence of solutions whenn≤2，and the asymptotic behavior of the classical solution was also established in[3].Later，Mizukami[19，20]extended these results to more particular situations.For higher dimensionsn≥3，similar results can be found in[16，42，44].Moreover，for when the chemotactic sensitivitiesχ，ξdepend on the chemical concentrationw，the global existence and solvability for the chemotaxis system are presented in[19，21，23，44].On the other hand，for the case ofχ，a2＜0 andξ＞0，it is proven in[8，11]that model (1.4) possesses a unique global classical solution ifn≤3 andχ，ξ，μi，ai，αiandβi(i=1，2) satisfy some suitable conditions.Moreover，the authors also showed the asymptotic stabilization of an arbitrary global bounded solution to the system:whena1＜1 and bothμi(i=1，2) are sufficiently large，inL∞(Ω) ast→∞;whena1≥1 andμ2is sufficiently large，.For the parabolic-parabolic-elliptic model (1.4)，we refer to[6，17，22，25]and the references therein.

Now we come back to the reaction-diffusion model (1.1) for predator-prey interaction，featuring both prey and predator taxis mediated by two signals.There is an important mathematical difference between the known system (1.2) and (1.1) in the sense that the former exists as a useful Lyapunov functional，while the latter helps to deal with the complex interactions ofu，v，w，zand to establish such a functional.

To motivate our study，we recall some related works in this filed.For when model (1.1) is without kinetic terms (i.e.，μ1=μ2=0)，the authors in[30]explored the global boundedness and finite time blow-up for the parabolic-elliptic-parabolic-elliptic case.Similar results were also investigated in[43].Moreover，for the fully parabolic case，[41]showed that (1.1) withχ＜0 possesses a global bounded solution under the conditions thatbeing suitably small.In the attraction-attraction caseχ＜0，the results in presence of Lotka-Volterra competitive kinetics have been presented in[5，14，34，46，48].For instance，whenn=2，Black[5]established a global classical solution to system (1.1) witha2＜0.The large time behavior of an arbitrary global bounded solution was also discussed for ifare large enough.Recently，the authors in[14]obtained the existence of global bounded solutions to model (1.1) whenμ1，μ2are sufficiently large in three dimensional space.For more related results，we refer readers to[12，24，40].However，to the best of our knowledge，problem (1.1)，involving competition，cooperation and predator-prey dynamics，seems not yet to have been investigated.

Motivated by the above studies[8，11，16，18]，in this paper，we focus on the global dynamical properties of (1.1) under some explicit conditions regarding the parametersχ，ξ，μi，ai，αiandβi(i=1，2) whenn≤3.Compared with the works[8]and[18]，the difficulties in our case come from the fact that the signalsvandzin (1.1) are indirectly produced by the predatorwand the preyu，respectively and the competitive mechanism is more complicated，which makes the calculations more delicate.

Throughout this text，to investigate the global dynamical properties，we assume that the initial datau0，v0，w0，z0satisfy

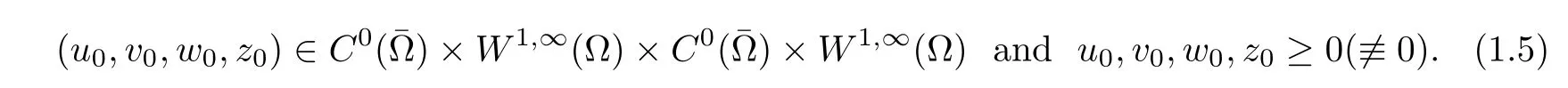
The first of our main results asserts the global existence of bounded solutions and is stated as follows:

Theorem 1.1Let Ω⊂R2be an arbitrary bounded domain with smooth boundary，and letχ，ξ，μi，ai，αiandβi(i=1，2) be positive constants satisfying 4μ1a1＞μ2a22.Then，for any initial value (u0，v0，w0，z0) satisfying (1.5)，problem (1.1) has a unique global classical solution (u，v，w，z).Furthermore，there exists some constantC＞0 that is independent oftsuch that

Remark 1.2In Theorem 1.2 of[34]，the global boundedness of solutions to the twocompeting-species chemotaxis system (1.1) in two dimensional space was presented without any restrictions onμi，ai(i=1，2).The reason for this is that

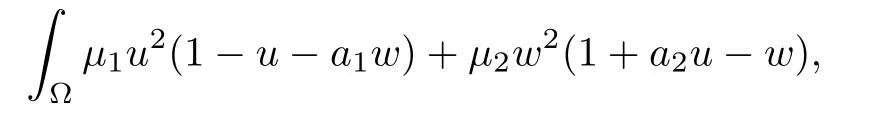
hence we can derive theL2-estimates ofuandw.

Remark 1.3In an arbitrary smooth bounded domain，whenn=1，we can obtain a similar result by a similar process as to that in the proof of Theorem 1.1 without any restrictions onχ，ξ，μi，ai，αiandβi(i=1，2).

In the three dimensional space，the boundedness property also holds.

Theorem 1.4Let Ω⊂R3be an arbitrary bounded domain with smooth boundary，and letμ1，μ2，a1，a2，αiandβi(i=1，2) be positive constants satisfyingα1，α2≥and

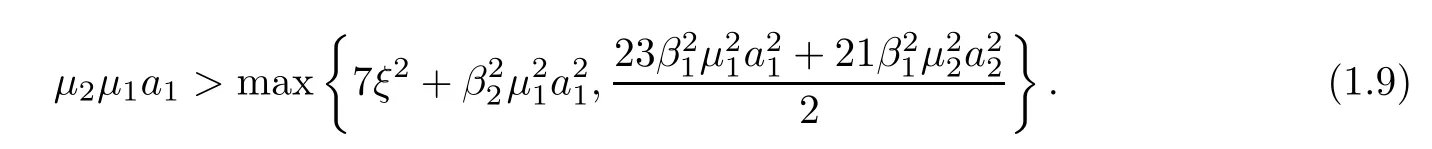
Then，for any initial value (u0，v0，w0，z0) fulfilling (1.5)，problem (1.1) possesses a unique global classical solution (u，v，w，z) which is bounded in the sense that (1.6) holds.

Remark 1.5The inequalities (1.7)–(1.9) can hold by settingμ1=μ2=α1=α2=β1=χ=ξ=0.02.

Remark 1.6We remark that Theorem 1.1 and Theorem 1.4 also hold for chemo-attraction or chemo-repulsion，i.e.，χξ＜0.Moreover，it is easy to find that ifμ1a1=μ2a2=β1=β2=1，then conditions (1.8) and (1.9) are consistent with (1.5) in[18].

By some adaptation of the approaches invented in[8，18]，the main results in what follows describe the asymptotic behavior and convergence rates for the global bounded solutions.

Theorem 1.7Let Ω⊂Rn(n≤3) be a bounded domain with a smooth boundary.Suppose thatμ1，μ2，a2，α1，α2，β1，β2＞0 and 0＜a1＜1 satisfy the relations

and the (u，v，w，z) is the global bounded classical solution of (1.1) with the initial data (u0，v0，w0，z0) satisfying (1.5).Then there exists constantC1＞0 andι1＞0 independent oftsuch that

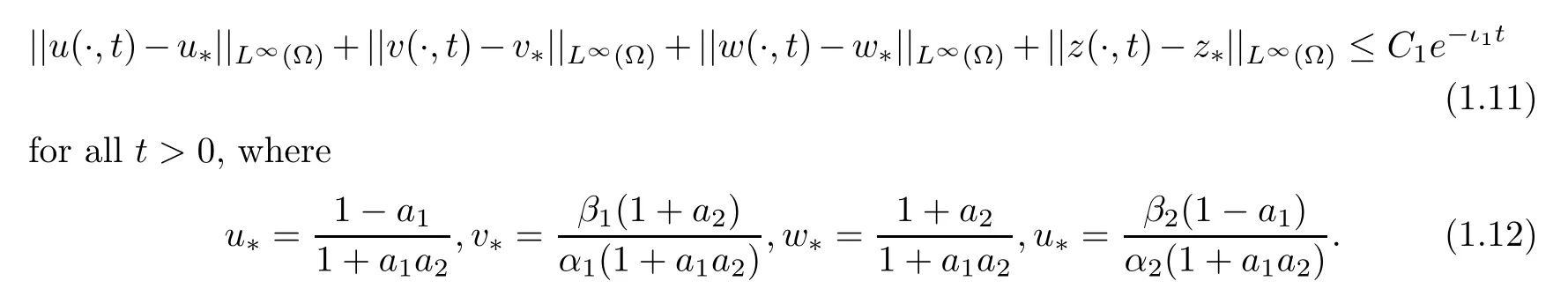
Theorem 1.8Let Ω⊂Rn(n≤3) be a bounded domain with a smooth boundary，and letμ1，μ2，a2，α1，α2，β1，β2＞0 anda1≥1.Suppose that (u，v，w，z) is the global bounded classical solution of (1.1) with the initial data (u0，v0，w0，z0) satisfying (1.5).Then the following properties hold:

(1) Ifa1＞1 and

then there are constantC2＞0 andι2＞0 independent oftsuch that，for allt＞0，

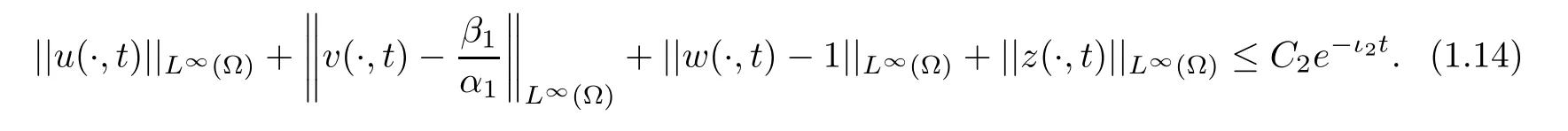
(2) Ifa1=1 and (1.13) holds，then there exist constantsC3＞0 andι3＞0 independent oftsuch that，for allt＞0，

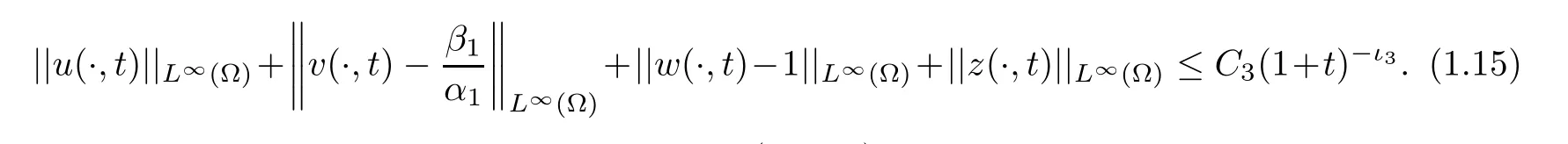
Remark 1.9In the higher dimensions (n＞3)，we can get the same conclusions as in Theorem 1.7 and Theorem 1.8，based on establishing the boundedness of a solution to (1.1).

The plan of the rest of this paper is organized as follows:in Section 2，we collect some basic properties of the local solvability and establish the some important estimates for the solution to system (1.1).In Section 3，we focus our attention on the global bounded solutions of (1.1) whenn=2 andn=3.In this section，crucial steps in the proof of Theorem 1.1 consist of establishingL2-estimates ofuandw.To this end，we invoke the conditionto guarantee the boundedness ofwhich is different from the argument in the proof of Theorem 1.2 in[34].Then，we complete the proof by settingp=1 andn=2 in Lemma 2.5.Similarly，the idea for the proof of Theorem 1.4 is to prove the bounde forTo achieve this，we give a suitable upper bound of the coupled functional

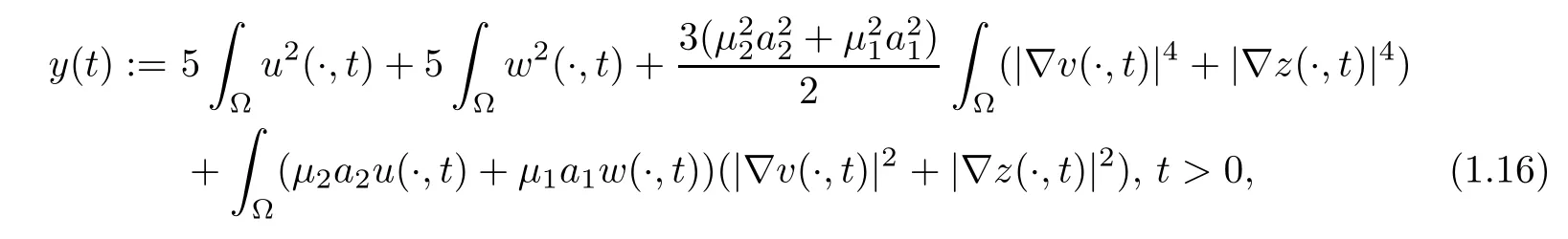
which technically deals with the termsΩuw(|∇v|2+|∇z|2).These thereby-obtained boundednesses，in conjunction with some suitable bootstrap arguments，result in our conclusion.In the final section，we mainly study the global asymptotic behavior of solutions and the convergence of equilibria to model (1.1) by some energy-type functionals similar to[3，34].

2 Preliminaries

Here，we first state the existence of a unique local-in-time classical solution to (1.1) in a follow lemma:

Lemma 2.1Let Ω⊂Rn(n≥1) be a smoothly bounded domain，and letχ，ξ，μi，ai，αiandβi(i=1，2) be positive constants.Assume that the initial data (u0，v0，w0，z0) satisfies (1.5).Then there existTmax∈(0，∞]and uniquely local non-negative classical functions

which solves (1.1) classically in Ω×[0，Tmax) for allt＞0.Moreover，ifTmax＜∞，then we have

ProofDenotingU=(u，v，w，z)∈R4，then system (1.1) can be written as

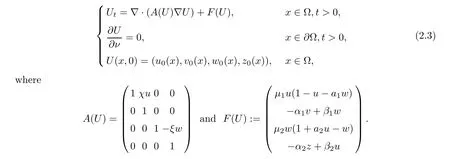
According to similar discussions in[1]，we obtain (2.1) and (2.2) immediately.Moreover，the nonnegativity ofu，v，w，zcan be checked by the maximum principle. □

We now state the following properties on the total mass ofu，win (1.1):

Lemma 2.2Letn≥1.The unique solution (u，v，w，z) of (1.1) satisfies

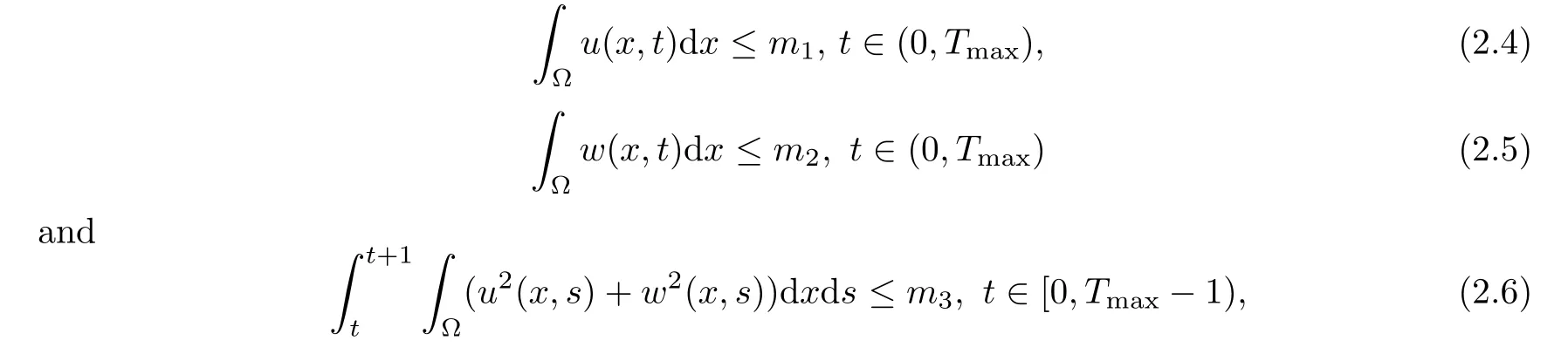
wheremi＞0(i=1，2，3).

ProofIntegrating the sum ofμ2a2times the first equation andμ1a1times the third equation in (1.1) over Ω，we use Young’s inequality to estimate that

for allt∈(0，Tmax).Settingy(t):=c1:=min{μ1，μ2}，we havey′(t)+c1y(t)≤μ1μ2(a1+a2)|Ω|，which implies (2.4) and (2.5) by an ODE comparison principle.

Moreover，integrating identity (2.7) on (t，t+1) and using (2.4)–(2.5) yields that

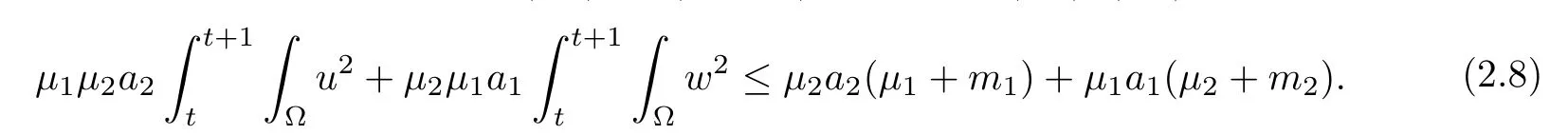
This implies (2.6)，by denoting□

For further a priori estimates from the properties asserted from Lemma 2.2，we give the following auxiliary conclusion which was stated in[3]:

Lemma 2.3LetT＞0 and assume thaty∈C1((0，T))∩C0([0，T)) satisfies

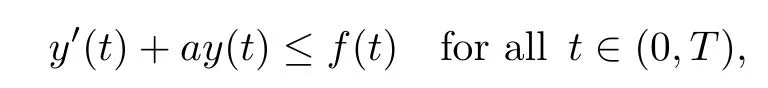
with somea＞0 andf∈C0([0，T)) for which there is a constantb＞0 such that

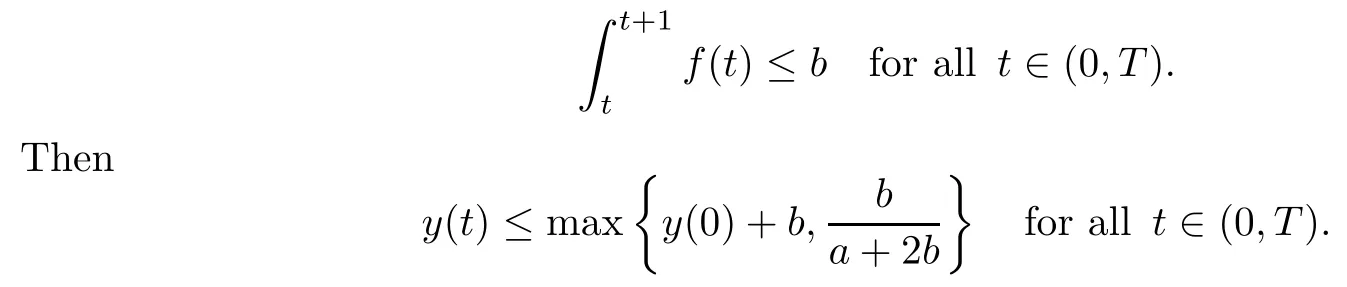
Here，we derive the bounds for ‖∇v‖L2(Ω)，‖∇z‖L2(Ω)and the spatio-temporalL2-estimate of Δv+Δz，which are crucial in our later proof.

Lemma 2.4Let (u，v，w，z) be a solution of (1.1).Then there are constantsKi(i=1，2，3)＞0 independent oftsuch that

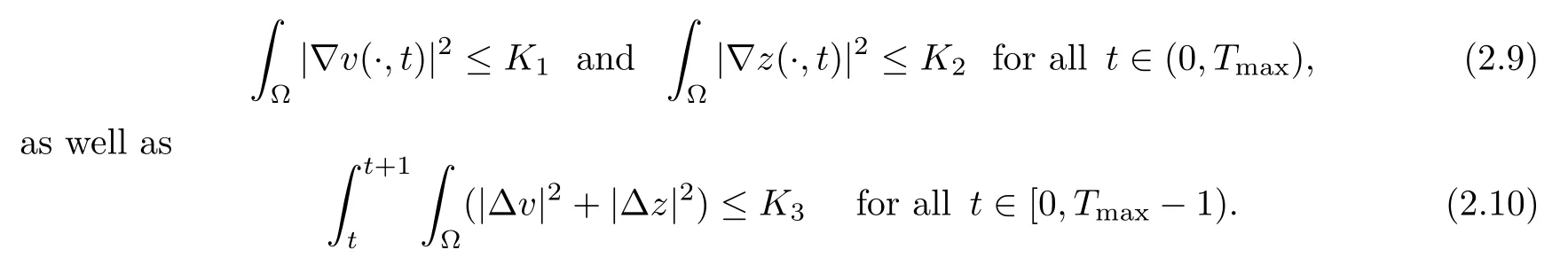
ProofWe test the second equation of model (1.1) with-Δvand integrate it by parts to obtain

Hence，Lemmas 2.2 and 2.3 imply that there exists a constantK1＞0 such thaty(t)≤K1.We can apply similar steps for the fourth equation of (1.1) to verify the bound forIt remains to prove (2.10).Indeed，by integrating (2.12) over (t，t+1)，we have

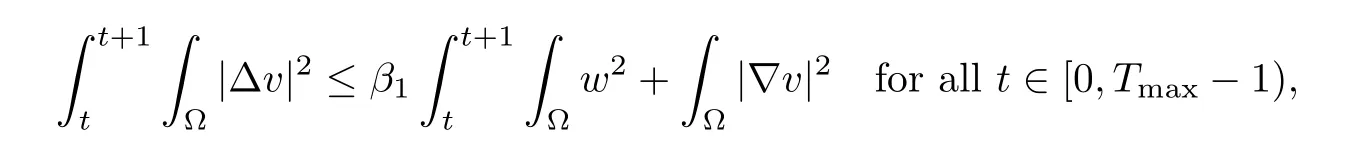
which，together with the bound forand Lemma 2.2，entails the boundedness ofSimilarly，we can derive the spatio-temporalL2-estimate of Δzand thereby complete the proof. □

To prove global existence and boundedness in the casen≤3，we exploit the following statement on the extensibility and regularity of solutions known to be bounded inL∞((0，Tmax);Lp(Ω)) for somep＞:

Lemma 2.5Let Ω⊂Rn(n≥1) be a bounded domain with a smooth boundary and let (u，v，w，z) be the solution of (1.1).Suppose that there exists a numberp≥1 andp＞for which

Furthermore，there areθ∈(0，1) andC＞0 such that

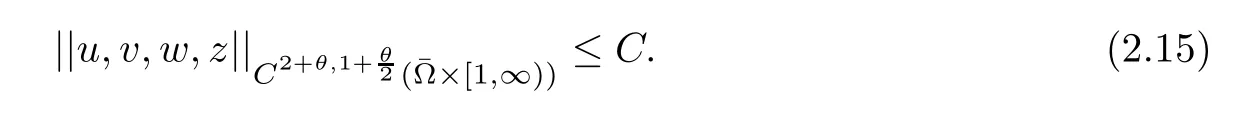
ProofOne can prove this lemma by a similar argument as to that in the proof of Lemma 2.6 in[3]，hence，we omit the details here. □

3 Boundedness

In this section，we focus on investigating the global boundedness of solutions to (1.1) in two or three dimensional space.

3.1 Boundedness of n≤2

To prove Theorem 1.1，we shall derive theL2-estimates ofu，w.

Lemma 3.1Let Ω⊂R2be a bounded domain with a smooth boundary，and letχ，ξ，μi，ai，αiandβi(i=1，2)＞0 satisfyThen there is a constantC＞0 such that the solution of (1.1) satisfies

ProofTesting the first equation in (1.1) byuand integrating it over Ω，we derive that

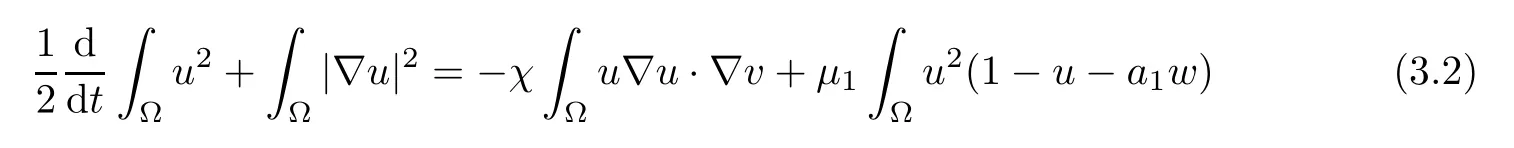
for allt∈(0，Tmax).Applying Hlder’s inequality，we deduce that

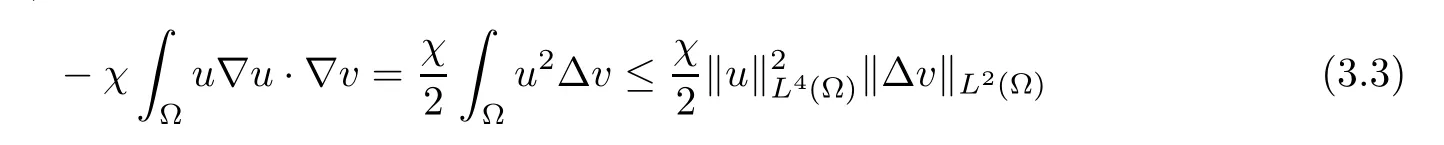
for allt∈(0，Tmax).Here，we further use the Gagliardo-Nirenberg inequality to estimate that

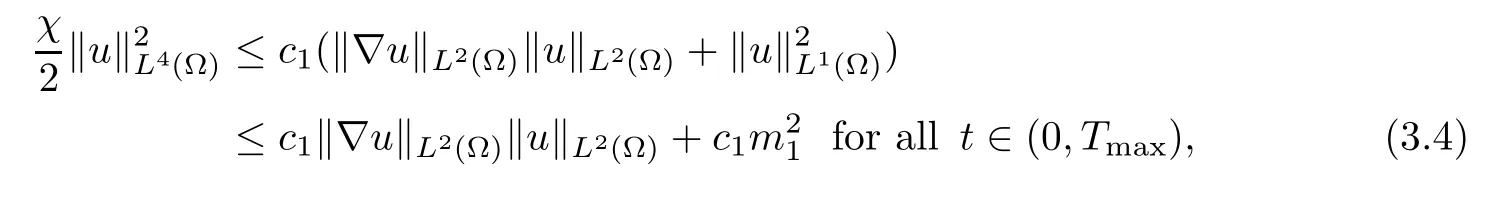
wherec1is a positive constant.This implies that

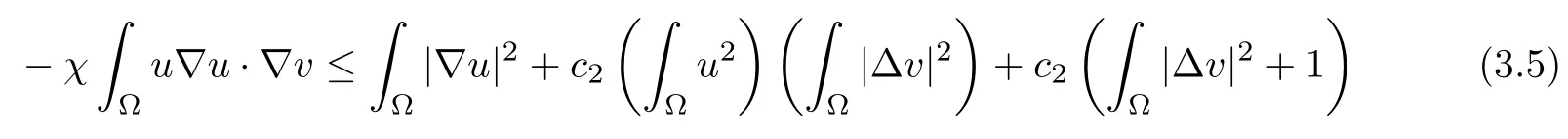
for allt∈(0，Tmax)，with somec2＞0.Then，we rewrite (3.2) as

for allt∈(0，Tmax).A similar argument as to that used for the above inequalities entails that

for allt∈(0，Tmax)，with somec3＞0.Collecting (3.6) and (3.7)，we find that

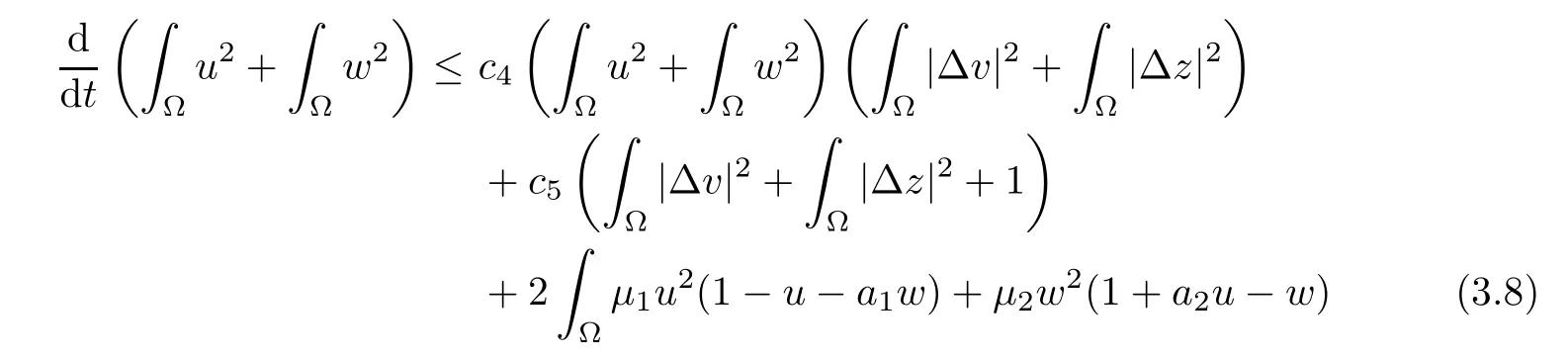
for allt∈(0，Tmax)，withc4:=max{2c2，2c3}andc5:=2c2+2c3.Then，we use Young’s inequality to obtain that

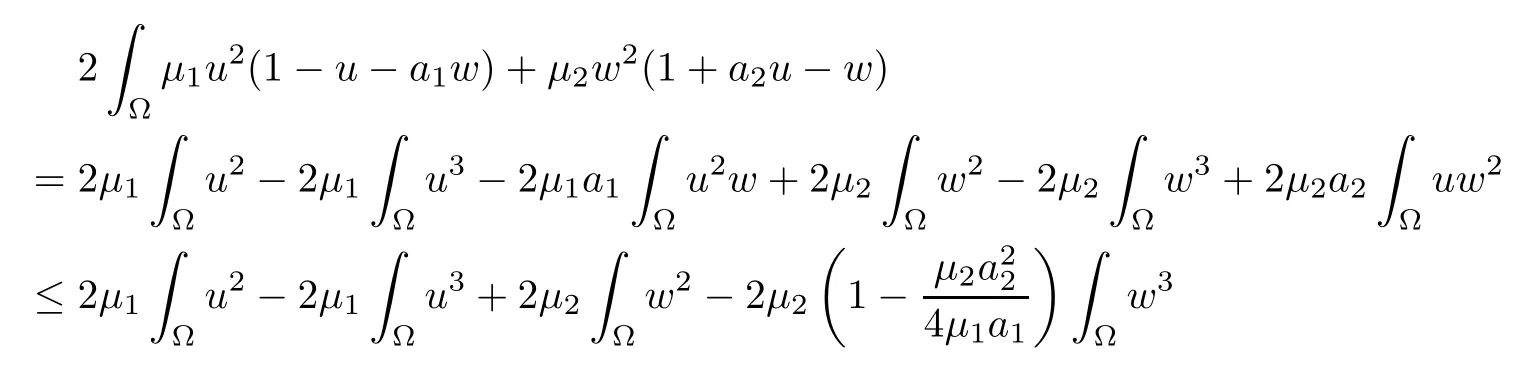
for allt∈(0，Tmax).In view ofit follows Young’s inequality again that there exists a constantc6＞0 such that

for allt∈(0，Tmax).Hence，we conclude that

for allt∈(0，Tmax)，withc7:=c5+c6.From Lemma 2.4，one can findc8＞0 such that

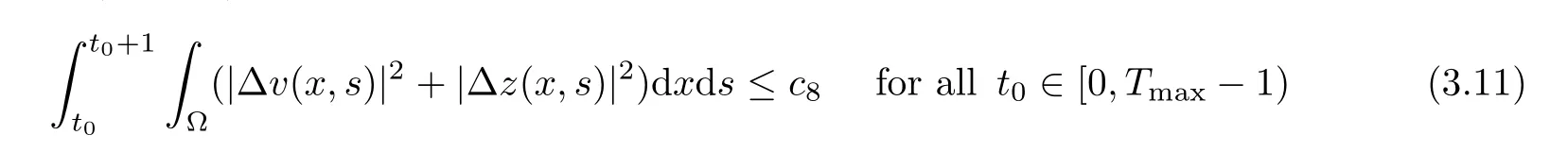
and fixingt∈(0，Tmax)，we can get from Lemma 2.2 that there existst0∈[0，Tmax) such thatt-1≤t0≤tand

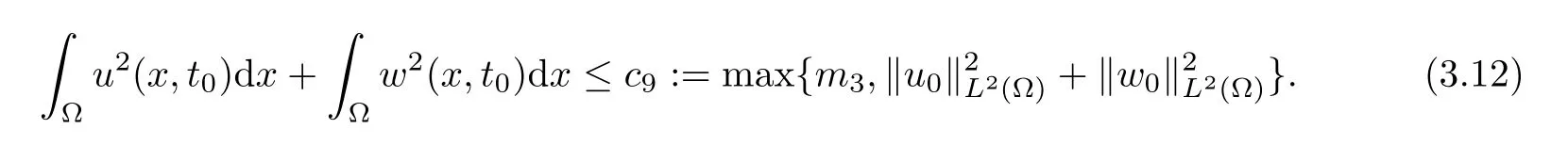
Then，integrating (3.10) on (t0，t)，and combining (3.11) and (3.12)，it holds that

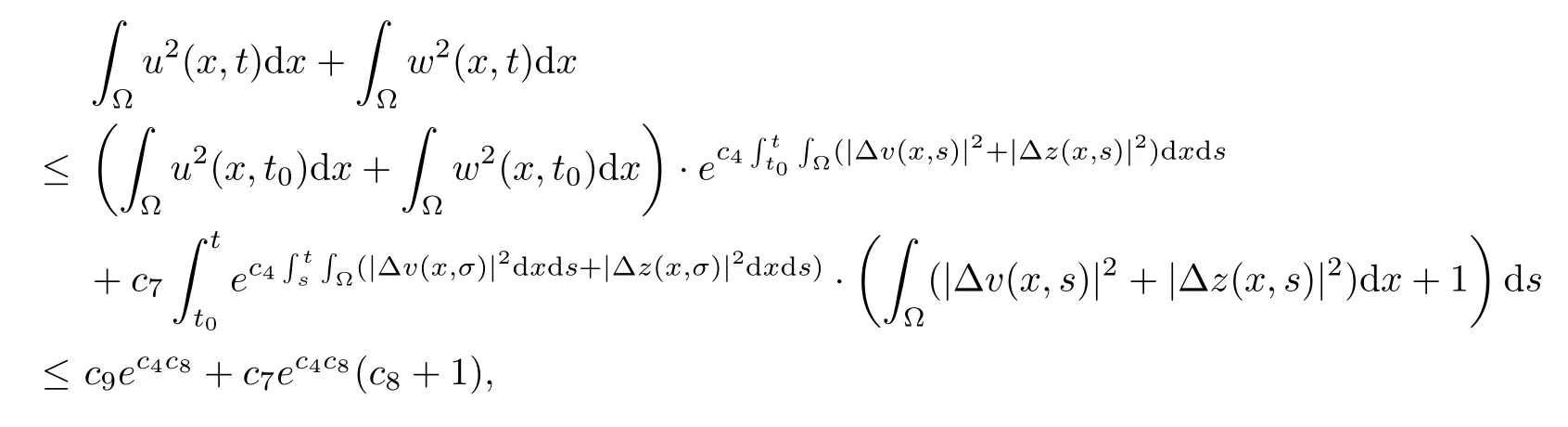
due tot≤t0+1.The proof is completed. □

Proof of Theorem 1.1Using Lemma 2.5 withp=2 and Lemma 3.1 whenn=2，the results of Theorem 1.1 are proved immediately.In particular，forn=1，we can apply Lemma 2.2 and Lemma 2.5 withp=1 to obtain the same conclusion. □

3.2 Boundedness of n=3

In this subsection，we shall present the proofs for Theorem 1.4.To begin with，some differential inequalities for the coupled functional in (1.16) are stated as follows:

Lemma 3.2Letn=3，χ，ξ，μi，ai，αiandβi(i=1，2)＞0.Then the solution (u，v，w，z) of (1.1) fulfills that

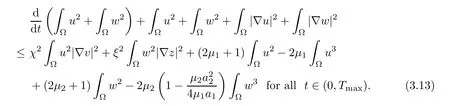
ProofTo achieve inequality (3.13)，we take theL2inner product of the first and third equations in (1.1) with 2uand 2w，respectively，and apply Young’s inequality to estimate

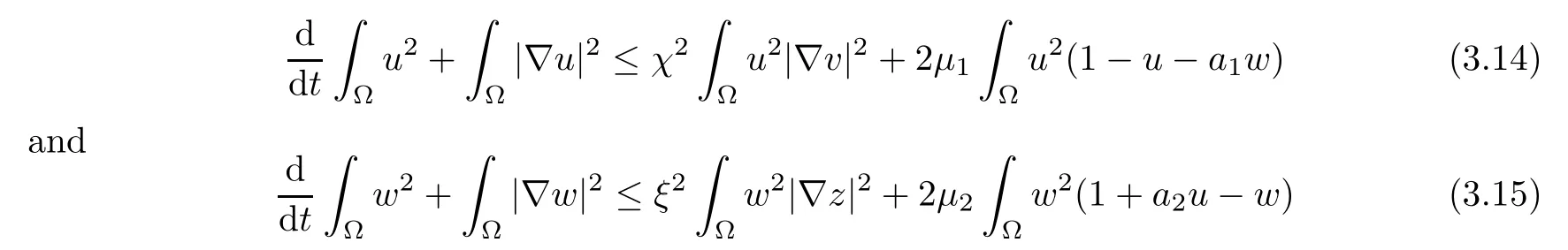
for allt∈(0，Tmax).Collecting the sum of (3.14) and (3.15) implies that

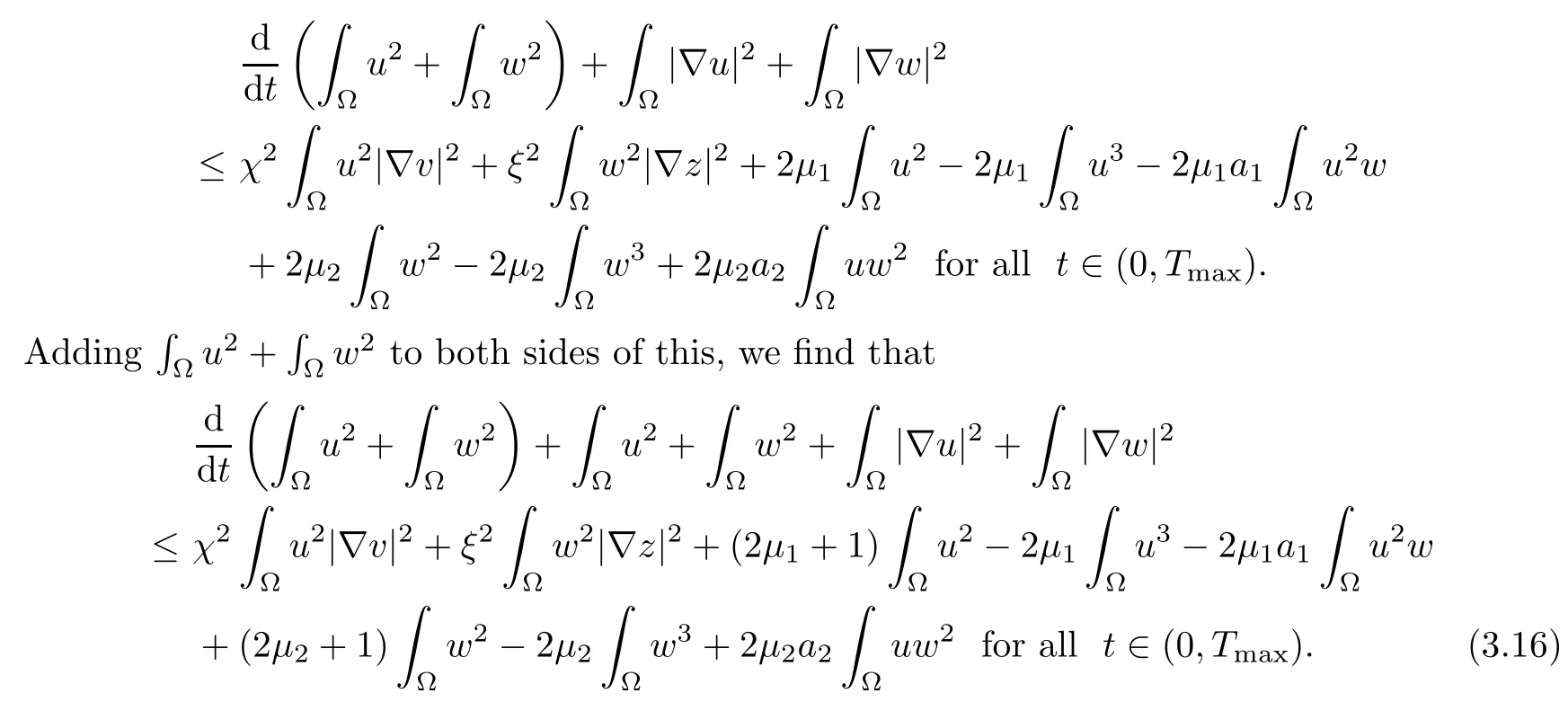
Then，we invoke Young’s inequality again to derive that

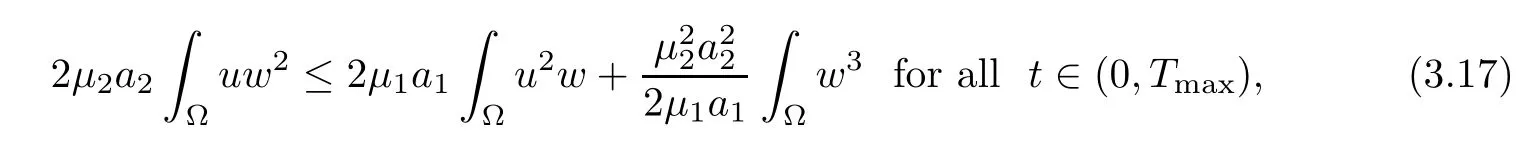
which，along with (3.16)，implies (3.13). □

Lemma 3.3Letn=3，χ，ξ，μi，ai，αiandβi(i=1，2)＞0.Then the solution (u，v，w，z) of (1.1) satisfies

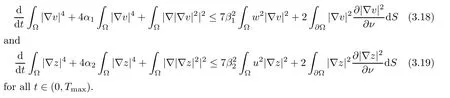
ProofBy a straightforward computation regarding the second equation in (1.1)，we invoke the identityto get that

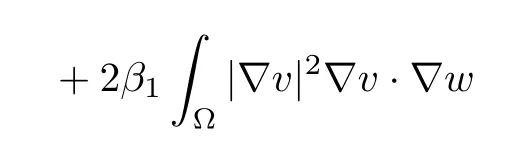
for allt∈(0，Tmax).Recalling the inequality|Δv|2≤3|D2v|2and using Young’s inequality，one can see that

for allt∈(0，Tmax).Hence，(3.18) can be proved by collecting the above inequalities.Moreover，we can obtain (3.19) by a discussion similar to that in the proof of (3.18). □

Lemma 3.4Letn=3，χ，ξ，μi，ai，αiandβi(i=1，2)＞0.Then the solution (u，v，w，z) of (1.1) fulfills that

ProofEvaluating the derivative ofwe use the identity∇v·again to estimate that

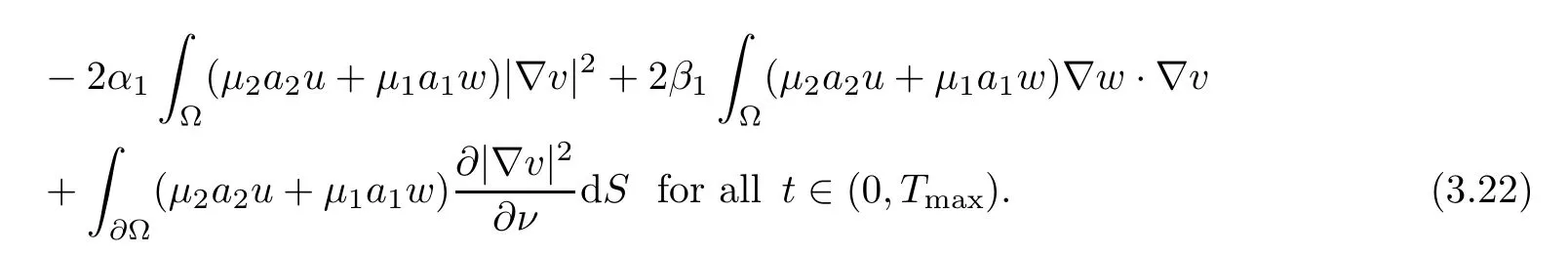
By another application of Young’s inequality，it holds that，for allt∈(0，Tmax)，

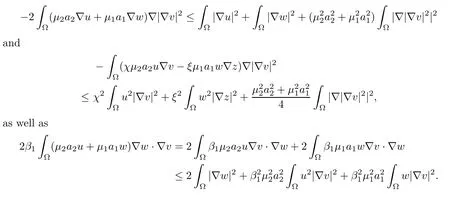
For the third term on the right hand side of (3.22)，it follows from the nonnegativity ofuandwthat

The above results lead to inequality (3.20).For (3.21)，we can verify things in a similar fashion.□

Upon a linear combination of (3.13)，(3.18)–(3.19) and (3.20)–(3.21)，we now carry out the following inequality:

Lemma 3.5Letn=3，χ，ξ，μi，ai，αiandβi(i=1，2)＞0.Then the solution (u，v，w，z) of (1.1) fulfills，for allt∈(0，Tmax)，that

Proof(3.23) results from (3.13)，(3.18)–(3.19) and (3.20)–(3.21)，by a direct calculation. □

With Lemma 3.5 in hand，we now estimate the boundedness of

Lemma 3.6Supposing that the conditions of Theorem 1.4 hold，there exists a constantC＞0 such that the solution of (1.1) satisfies

Next，we use the Gagliardo-Nirenberg inequality and Young’s inequality to obtain that

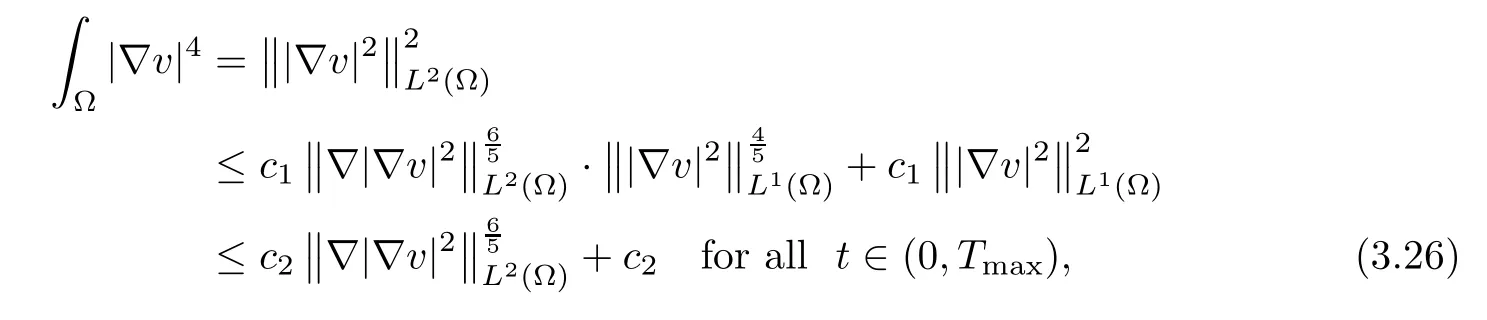
with somec1，c2＞0.Similarly，we have

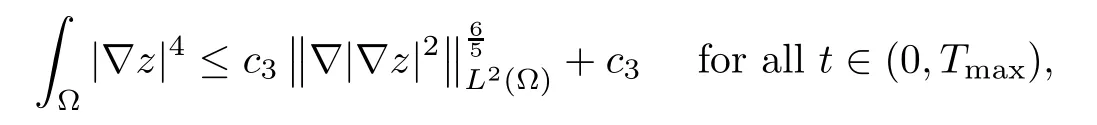
with somec3＞0.Hence，with these estimates，we recall Young’s inequality again to derive that

Hence，we can derive that

which，together with Young’s inequality，revealsy′(t)+y(t)≤c10for allt∈(0，Tmax).Then，we obtain from an ODE comparison thaty(t)≤c11for allt∈(0，Tmax)，wherec11:=max{y(0)，c10}.This implies (3.24). □

Proof of Theorem 1.4In view of Lemma 2.3 and Lemma 3.6，we attain the desired result of Theorem 1.4 by an aregument similar as to that for the proof of Theorem 1.1. □

4 Stabilization

In this section，we investigate the asymptotical behavior of solutions to (1.1).To this end，we shall prepare some basic results.

Lemma 4.1(See[4]) Suppose thatf:[1，∞)→R is a uniformly continuous nonnegative function and thatdsexists.Then

We next present a lemma which plays an important role in the proofs of Theorems 1.7 and 1.8.

Lemma 4.2Let∈R4be any solution of

and let (u，v，w，z) be a global bounded classical solution to (1.1).Assume that there are two decreasing functionsg1(t) andg2(t) on[t0，∞) for somet0＞0 such that

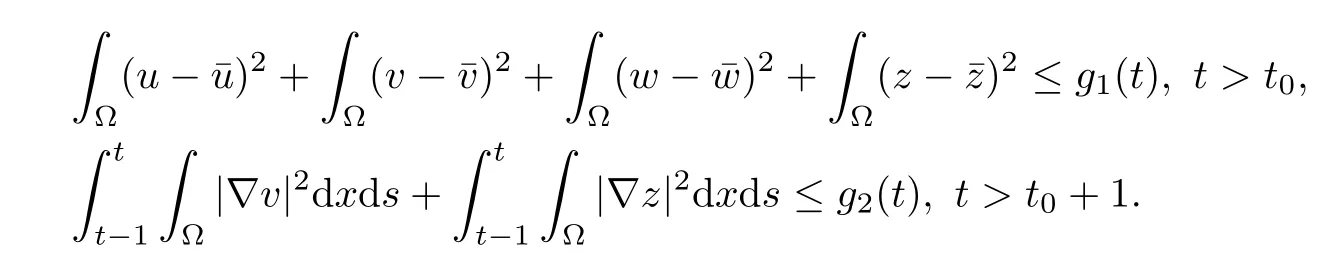
Then there exists a positive constantCsuch that，for allt＞t0+2，

ProofThis lemma can be proved by the same arguments as those used in Lemma 3.6 in[3]. □

4.1 Global stability of (u*，v*，w*，z*):Proof of Theorem 1.7

In this subsection，we shall show that if 0＜a1＜1，and bothare appropriately large，then the bounded solution (u，v，w，z) will stabilize to the constant stationary solution (u*，v*，w*，z*) defined in (1.12).To achieve this，we next derive the key estimate for the proof of Theorem 1.7 as follows:

Lemma 4.3Let (u，v，w，z) be a global bounded classical solution of (1.1) and 0＜a1＜1.If the conditions (1.10) hold，then there existς1，ς2＞0 andε1＞0 such that functionsE1andF1，defined by

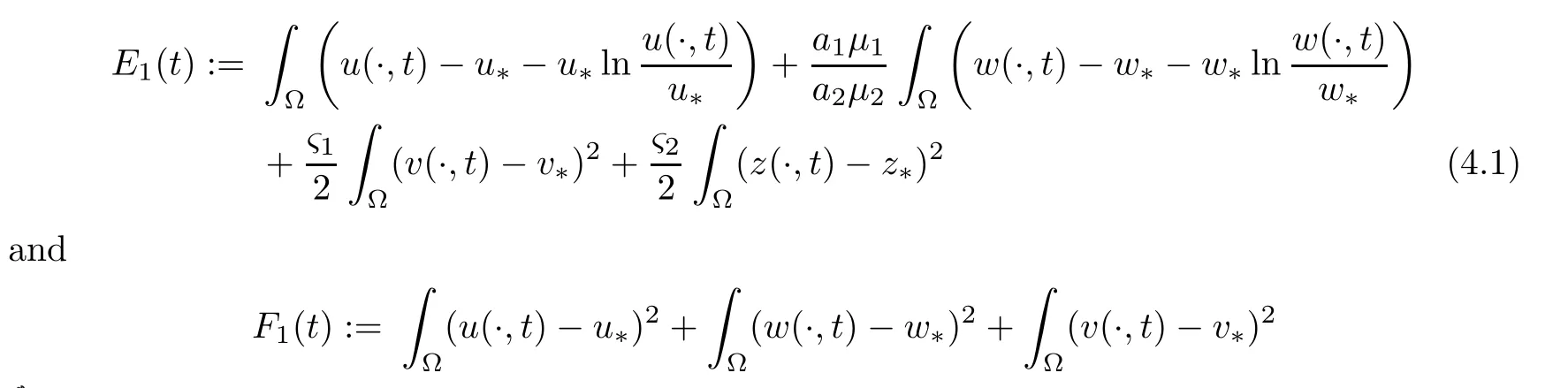
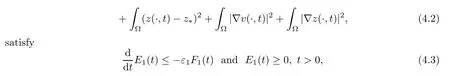
which implies that the following asymptotic behavior holds:

Then，by a similar argument as to that in Lemma 3.2 of[3]，we can obtain the nonnegativity ofA1(t) andB1(t)，and hence thatE1(t)≥0.With the definition ofA1(t)，B1(t) andC1(t)，it follows from a straightforward calculation that

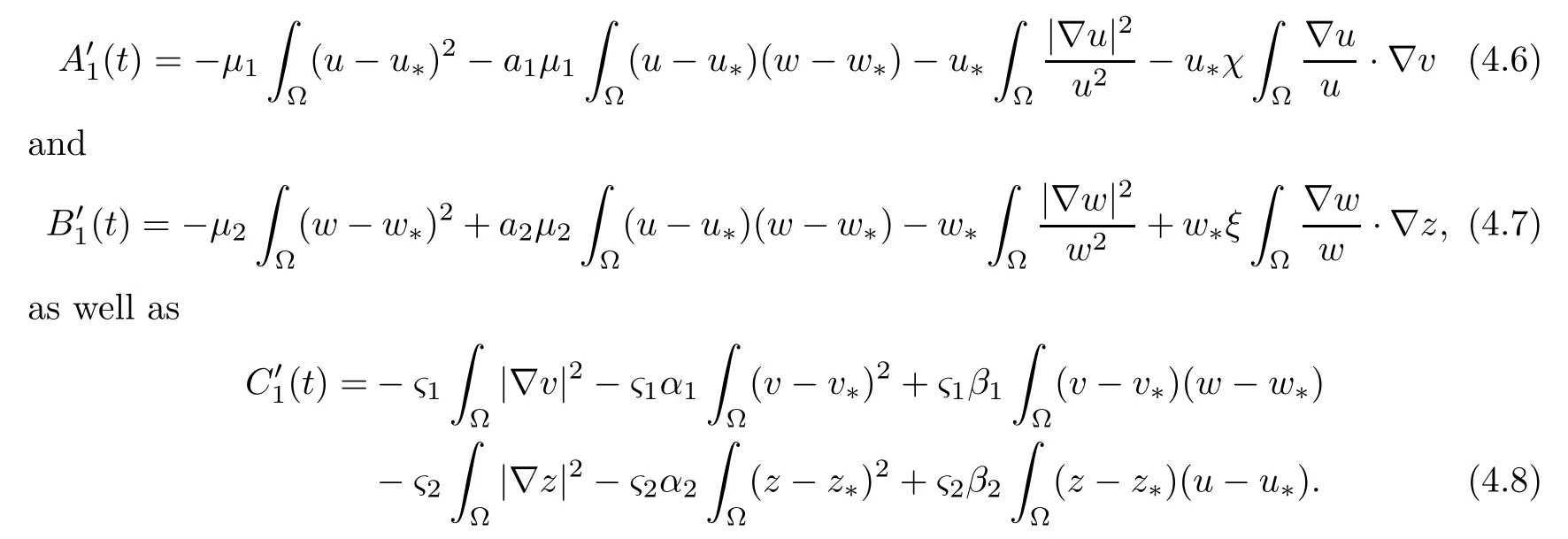
Collecting (4.5)–(4.8)，we obtain that，for allt＞0，

Next，we invoke Young’s inequality to estimate that

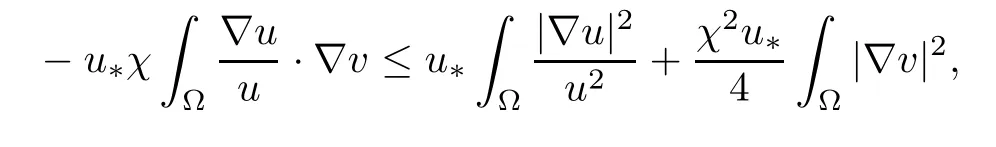
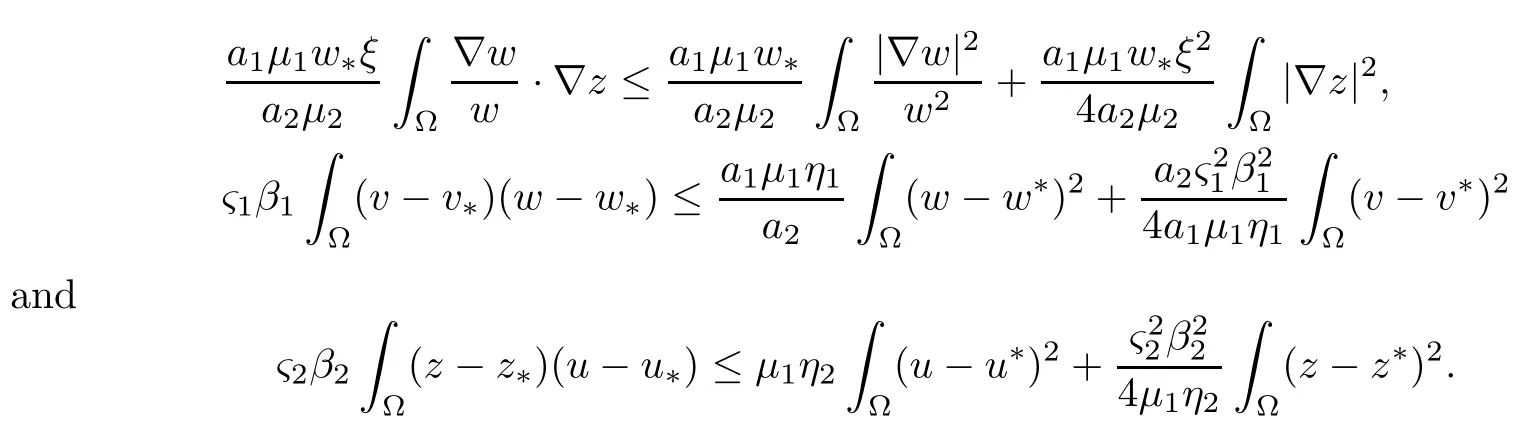
Inserting the above inequalities into (4.9)，one has that

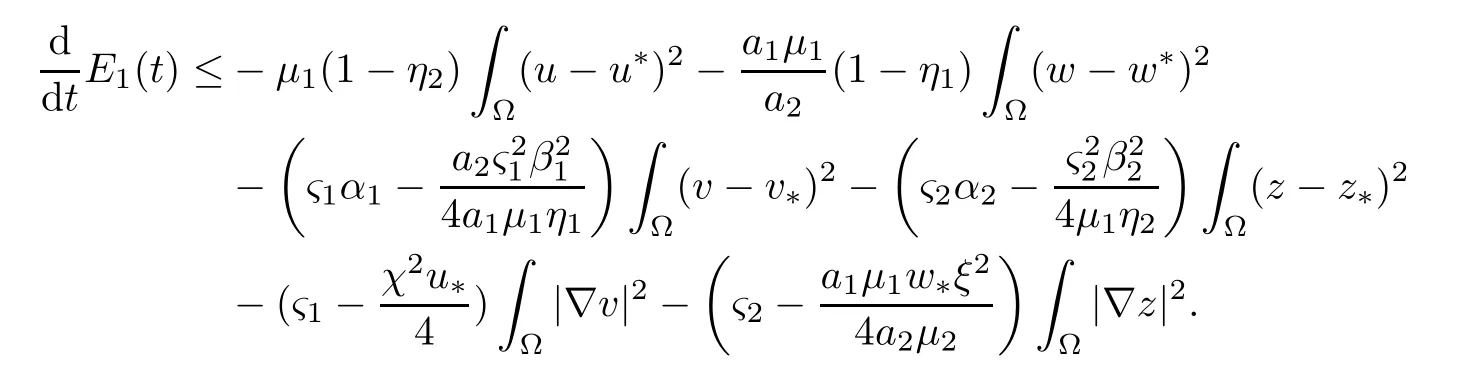
From the definition ofς1，ς2，we can choose suitableε1＞0 in order to complete the proof of (4.3).Furthermore，we define the functionHence，it follows from (4.3) that(t)≤-ε1F1(t)≤-ε1f1(t)，which，along withE1(t)≥0，reveals that

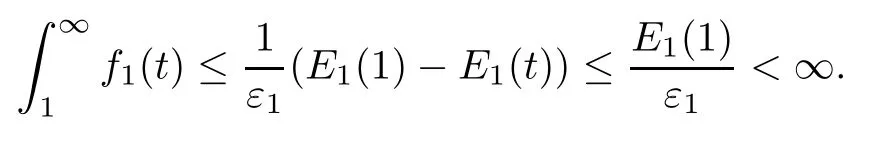
Using the regularity ofu，v，w，zand the fact thatf1(t) is uniformly continuous on[1，∞)，we infer from Lemma 3.1 of reference[3]that

Furthermore，it follows from (2.15) that，fort＞1，u(·，t)，v(·，t)，w(·，t)，z(·，t) are bounded in the spaceW1，∞(Ω).Then we can apply the Gagliardo-Nirenberg inequality ‖φ‖L∞(Ω)≤∀φ∈W1，∞(Ω) tou(·，t)-u*，w(·，t)-w*，v(·，t)-v*andz(·，t)-z*，respectively，to achieve (4.4). □

Proof of Theorem 1.7DefineH(s):=s-y*lns(s＞0) with a constanty*＞0.Then，one can derive that

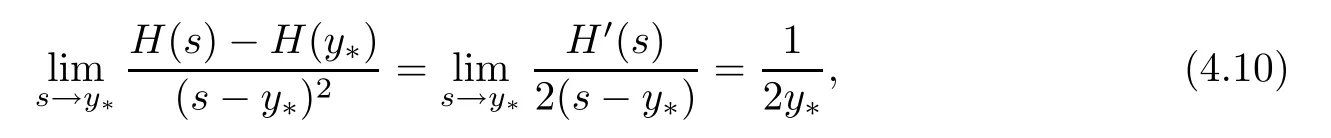
which，together with (4.4)，implies that

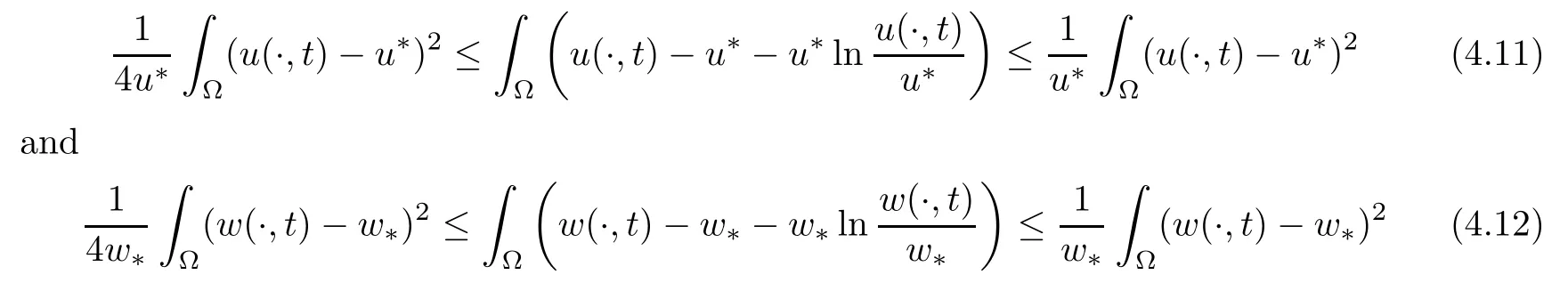
for allt＞t0＞0.Hence，by the definitions ofE1(t) andF1(t)，we have thatE1(t)≤c1F1(t) for somec1＞0 and allt＞t0.Plugging this into (4.3) yields thatfort＞t0.This results infor allt＞t0，withc2，Combining (4.11) with (4.12)，there is a constantc3＞0 such that

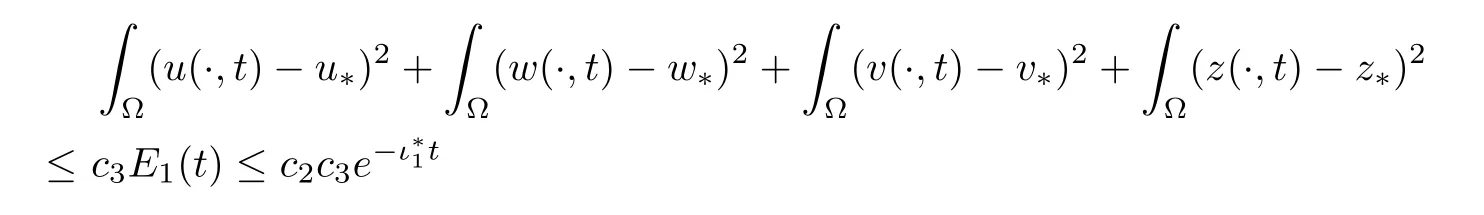
for allt＞t0.Moreover，one can findc4＞0 such that

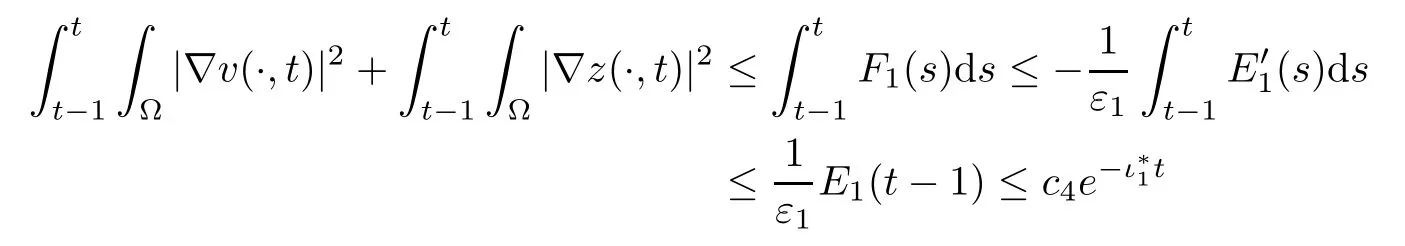
for allt＞t0+1.Finally，an application of Lemma 4.2 implies that (1.11) holds. □

4.2 Global stability of (0，，1，0):Proof of Theorem 1.8

In this case，applying an approach similar to that of Subsection 4.1，we shall prove that ifa1≥1 and ifis appropriately large，then the bounded solution (u，v，w，z) will converge to the constant stationary solution (0，，1，0).

Lemma 4.4Let (u，v，w，z) be a global bounded classical solution of (1.1) and leta1≥1.If condition (1.13) holds，then there areς3，ς4＞0 andε2＞0 such that functionsE2andF2，defined by

ProofThe nonnegativity ofE2(t) is obvious.From (1.13)，we find （η3∈(0，1) clos）e to 1 such thatHence，we can choosesuch thatE2(t) is rewritten as

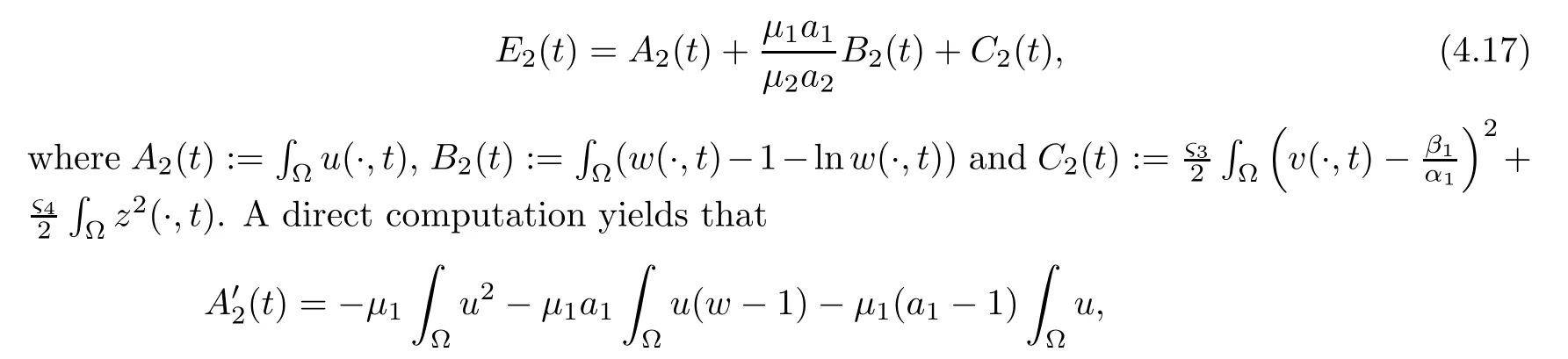
where we used Young’s inequality.Then，inserting the above estimates into (4.17)，we get that

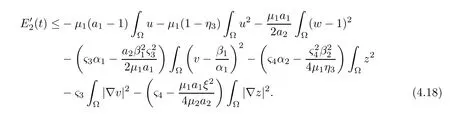
Using the argument for the proof of Lemma 4.3 can verify (4.15) and (4.16). □

Proof of Theorem 1.8(1)Sinceby invoking ideas similar to those used in deriving the previous estimates，we recall (4.16) to obtain that

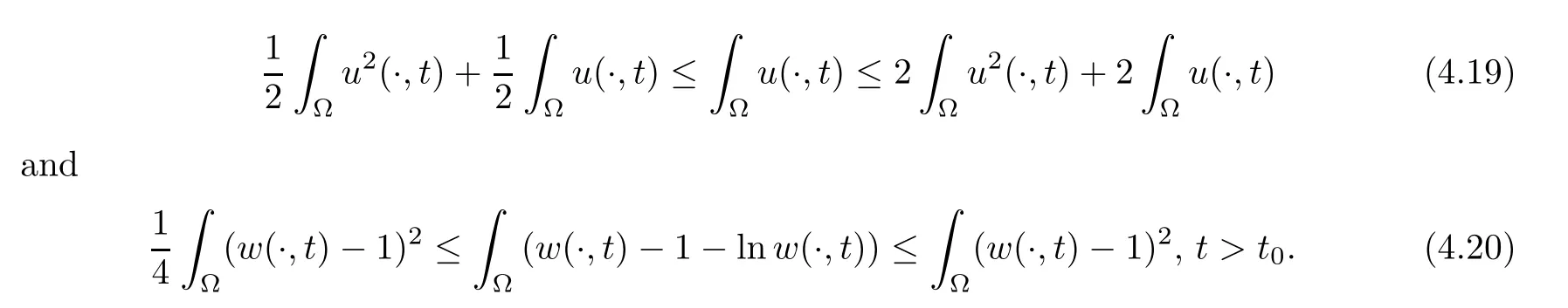
Then，combining the definitions ofE2(t) andF2(t) with the right inequalities of (4.19) and (4.20) yields that there existsc1＞0 such that，t＞t0，which implies that

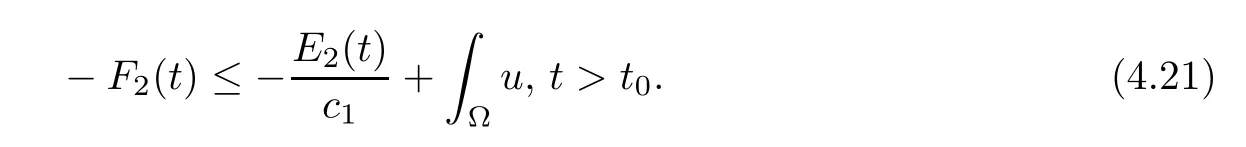
Due toa1＞1，without loss of generality，we pickε2＜μ1(a1-1) and insert (4.21) into (4.15) to estimate that

Consequently，we infer that there existc2＞0 and＞0 such thatfor allt＞t0.Therefore，with the left inequalities of (4.19)，(4.20) entails that

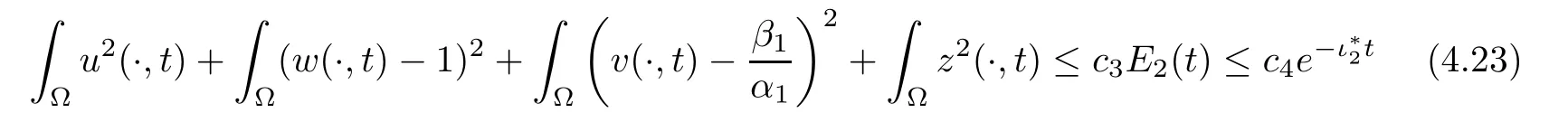
for allt＞t0，wherec3，c4＞0 are constants，and there is a constantc5＞0 such that

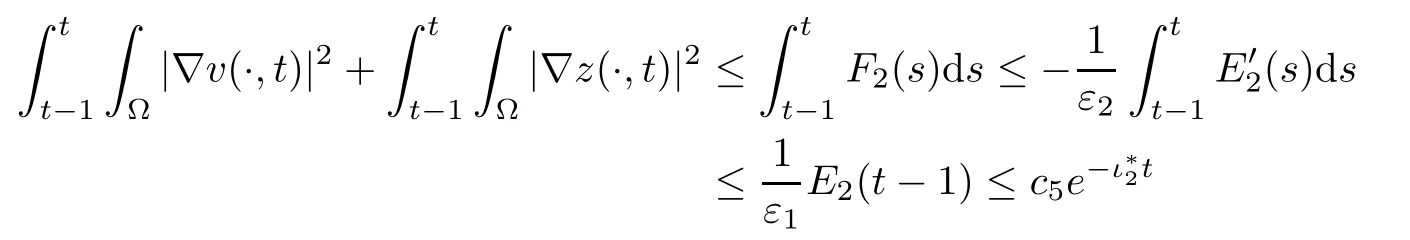
for allt＞t0+1.In view of Lemma 4.2，we assert that there existC1＞0 andι2＞0 independent oftsuch that (1.14) holds. □

Proof of Theorem 1.8(2)Whena1=1，the termuin (4.15) will disappear.Note that (4.19) and (4.20) also hold.In addition，in view of the definition ofE2(t)，F2(t) and inequality (4.20)，we know from Hlder’s inequality and the boundedness of (u，v，w，z) that

with some constantsc6，c7，c8，c9，c10＞0.This，along with (4.15)，yields that there is a positive constantc11such thatTherefore，we assert thatfort＞t0withc12＞0.Then，we know，by (4.19) with (4.20)，that

for allt＞t0+1.Furthermore，using Lemma 4.2 again can achieve (1.15).This completes the proof. □