ESTIMATES FOR EXTREMAL VALUES FOR A CRITICAL FRACTIONAL EQUATION WITH CONCAVE-CONVEX NONLINEARITIES*
Jianghao HAO (郝江浩)
School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China
E-mail:hjhao@sxu.edu.cn
Yajing ZHANG (张亚静)†
School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China
E-mail:zhangyj@sxu.edu.cn
Abstract In this paper we study the critical fractional equation with a parameter λ and establish uniform lower bounds for Λ,which is the supremum of the set of λ,related to the existence of positive solutions of the critical fractional equation.
Key words Multiple positive solutions;fractional Laplace problems;critical growth
1 Introduction
The fractional Laplacian appears in diverse areas,including flame propagation,the chemical reactions of liquids,population dynamics,geophysical fluid dynamics,and American option (see[1–7]and the references therein).Partial differential equations involving the fractional Laplacian have also attracted the attention of many researchers.
In this paper we consider the following critical problem involving the fractional Laplacian:
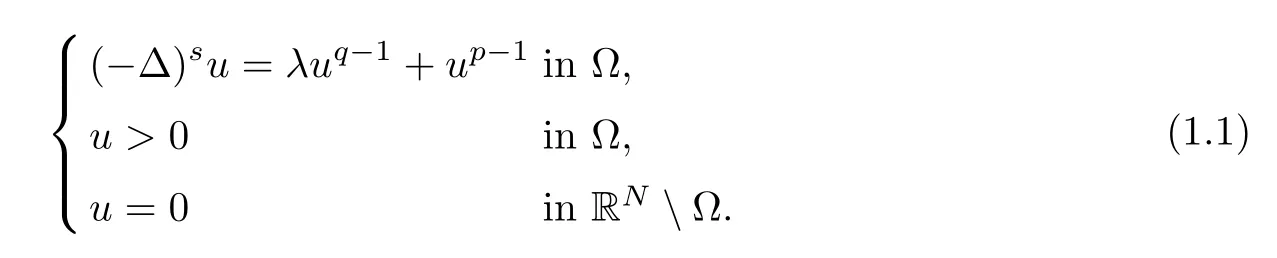
Heres∈(0,1) is fixed and (-Δ)sis the fractional Laplace operator,Ω⊂RN(N>2s) is a smooth bounded domain,andλis a real parameter.
The fractional Laplace operator (-Δ)s(up to normalization factors) may be defined as

whereK(x)=|x|-(N+2s),x∈RN.We will denote byHs(RN) the usual fractional Sobolev space endowed with the so-called Gagliardo norm

whileX0is the function space defined as

We refer to[8–10]for a general definition ofX0and its properties.The embeddingis continuous for anyand compact for anyr.The spaceX0is endowed with the norm defined as

By Lemma 5.1 in[9]we have(Ω)⊂X0.ThusX0is non-empty.Note that (X0,‖·‖X0) is a Hilbert space with the scalar product

Problems similar to (1.1) have also been studied in the local setting.In particular,Brezis and Nirenberg[11]studied the equation-Δu=|u|2*-2u+f(x,u),wheref(x,u) is a lower order perturbation of|u|2*-2uin the sense thatA typical example to which their results apply is-Δu=λ|u|q-2u+|u|2*-2u,whereλ>0 is a parameter and 2<q<2*.Ambrosetti et al.[12]investigated the following problem with concave-convex power nonlinearities:
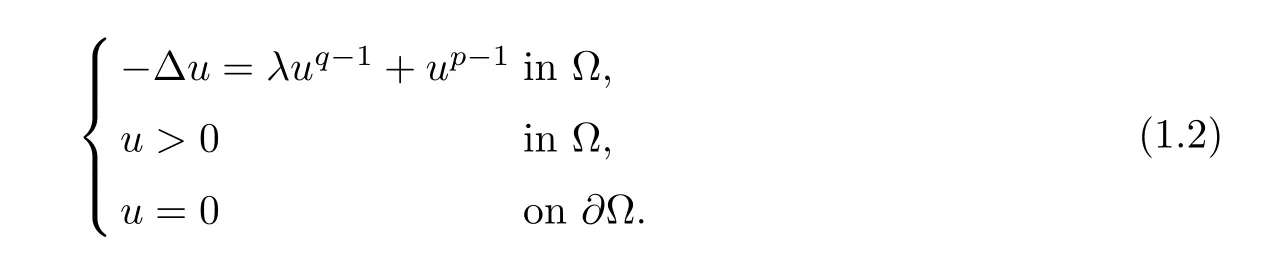
Here 1<q<2<p≤2*.They showed the existence and multiplicity of solutions to problem (1.2).After the work[12],several papers were devoted to problem (1.2);see for example[11,13–20].
Now,we focus attention on critical nonlocal fractional problems.It is worth noting here that problem (1.1) withλ=0 has no positive solution whenever Ω is a star-shaped domain;see[21,22].This fact motivates the perturbation termsλuq-1,since we are interested in the existence of positive solutions of (1.1).Servadei and Valdinoci[23,24]studied problem (1.1) withq=2,and obtained Brezis-Nirenberg type results.Barrios et al.[25]studied problem (1.1).Among other things,they proved that there existsλ*>0 such that problem (1.1) admits at least two positive solutions forλ∈(0,λ*),one positive solution forλ=λ*,and no positive solution forλ>λ*.Note that the results correspond to the nonlocal version of the main result of[12].We are interested in finding the values ofλ*at which the above transition occurs,and actually,we obtain some lower bounds forλ*.
Note that one can also define a fractional power of the Laplacian using spectral decomposition.A similar problem to that of (1.1),but for this spectral fractional Laplacian,was treated in[26–28].
In the context of our paper,we denote bySpthe best constant for the embedding ofX0intoLp(Ω);that is,

We denote by|·|rtheLr(Ω)-norm for anyr>1.u+=max{u,0}denotes the positive part ofu.
Our main result is as follows:
Theorem 1.1

This paper is organized as follows:in the next section,we give some lemmas.In Section 3,we prove the existence of a ground state solution of (1.1).In Section 4,we prove the existence of the second solution of (1.1) and Theorem 1.1.
2 Preliminaries
In this section,we prove several lemmas.
Taking into account that we are looking for positive solutions,we consider the energy functional associated with (1.1):

By the Maximum Principle (Proposition 2.2.8 in[29]) it is easy to check that critical points ofIλare the positive solutions of (1.1).
We define the Nehari manifold

Obviously,the Nehari manifold contains all the nontrivial critical points ofIλ.
Lemma 2.1The functionalIλis coercive and bounded from below on Nλ.
ProofFor everyu∈Nλ,we have

and consequently,Iλis coercive and bounded from below on Nλ,since 1<q<2. □
Define

Then,foru∈Nλ,we have
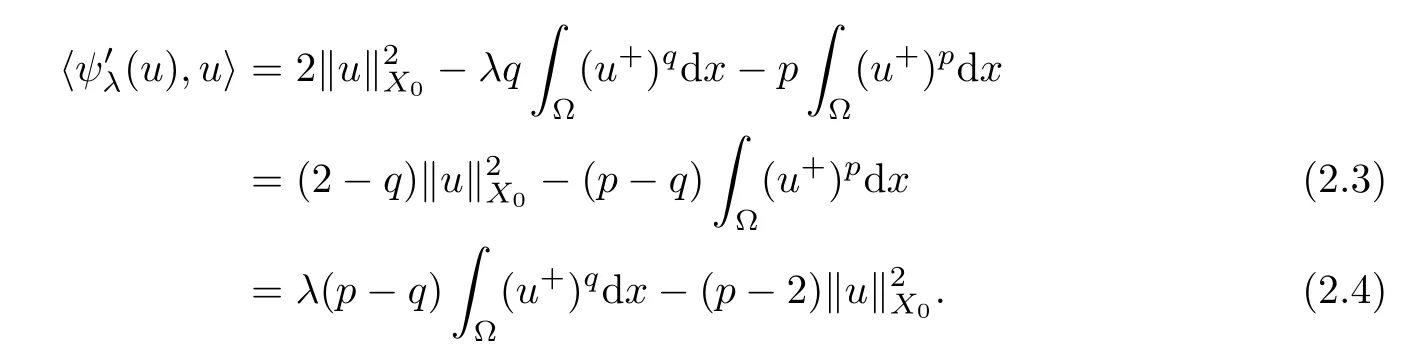
Adopting a method similar to that used in[30],we split Nλinto three parts:

Lemma 2.2Ifλ<Λ,then=Ø.
ProofAssume,by contradiction,that there existsu∈N0λ.By (2.3) and (2.4),we have

Thus,we get thatu≡0,which is impossible. □

Clearly,tu∈Nλif and only ifMoreover,

Thus,it is easy to see thattuif and only ifγ′(t)>0(or<0).Notice thatγis increasing on (0,tmax) and decreasing on (tmax,+∞) and thatγ(t)→-∞ast→+∞.
Direct computation yields that


Lemma 2.4Letλ∈(0,Λ).Then

ProofFor anyu∈,we have
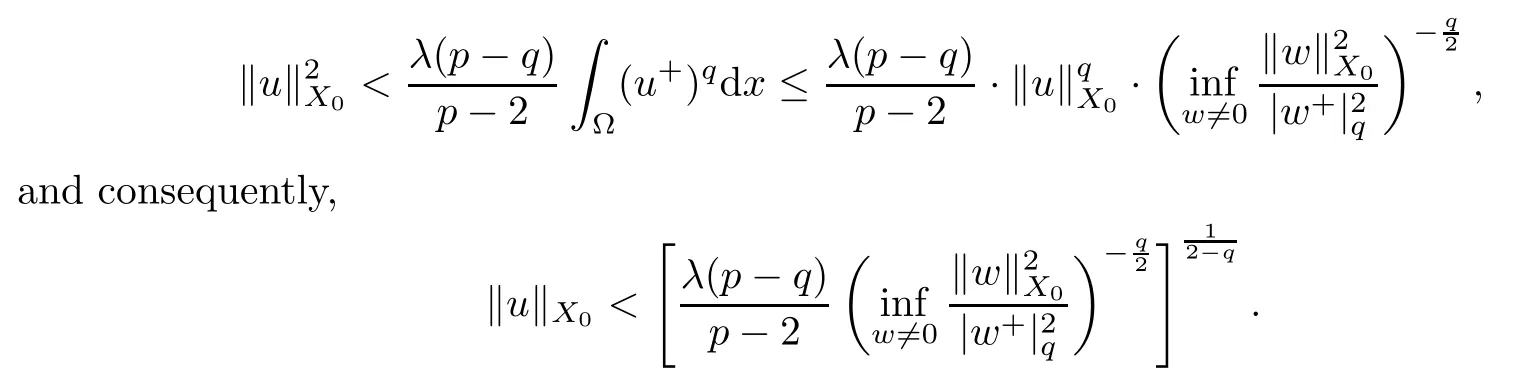
For anyv∈,we have

and consequently,

Sinceλ<Λ,we have
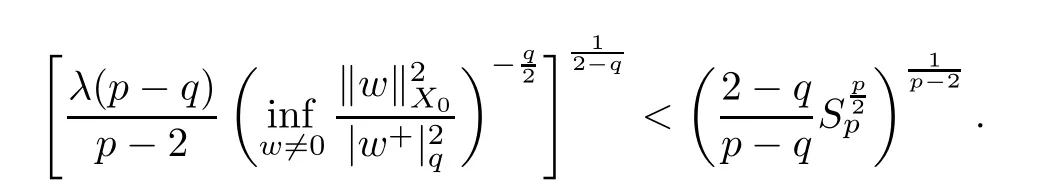
This completes the proof. □
Lemma 2.5Letλ∈(0,Λ).Thenare closed in theX0topology.
ProofSince,for any sequence,un→u0strongly inX0withun∈N+λ,it follows thatu0∈Nλ,and by Lemma 2.4 we derive that

In turn,it follows thatu0∈.Similarly,we can prove thatis closed. □
As a consequence of Lemma 2.2,we have
Lemma 2.6Givenu∈Nλ,there existsε>0 and a differential functionalt=t(w)>0,w∈X0,‖w‖X0<εsatisfying that

ProofDefineF:R×X0→R as follows:

SinceF(1,0)=0,and by Lemma 2.2,we obtain

and we can apply the implicit function theorem at the point (1,0) to get the results. □
3 Existence of a Ground State Solution
Applying Lemma 2.1,we define

In this section,we show that problem (1.1) has at least two positive solutions ifλ<Λ.To be precise,we will prove two propositions which guarantee one solution forand another solution for.
Lemma 3.1Forλ∈(0,Λ),there exists a (PS)αλsequence{un}⊂NλforIλ.
ProofApplying Ekeland’s variational principle[31]to the minimization problemαλ=,we have a minimizing sequence{un}⊂Nλwith the following properties:
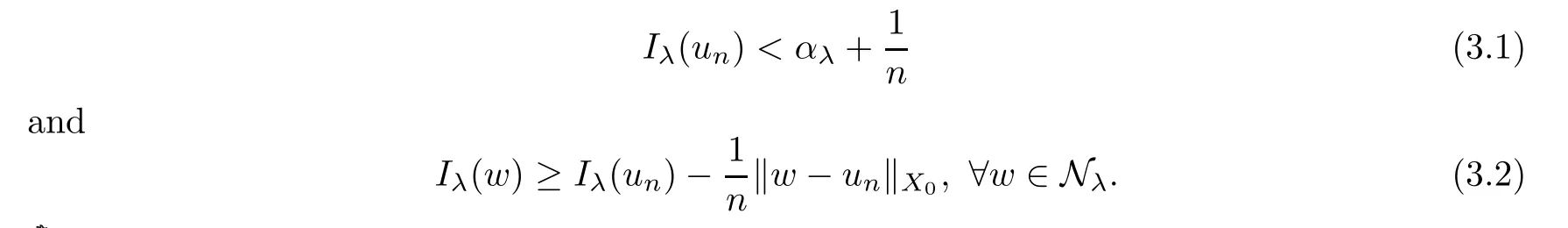
By (3.1) and Lemma 2.1,there exists a constantCλsuch that

Pickw0∈,and by Lemma 2.3 there existst(w0)>0 such thatt(w0)w0∈.By (2.3),we have that

By takingnlarge,from (3.1) and (3.4),we have that
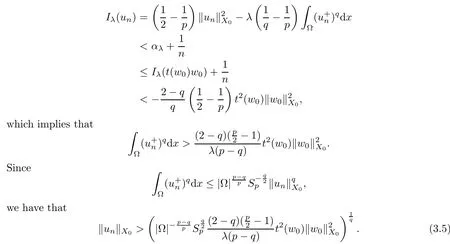
Letv∈X0with ‖v‖X0=1.Applying Lemma 2.6 withu=unandw=ρv,ρ>0 small,we gettn(ρv) such thatwρ:=tn(ρv)(un+ρv)∈Nλ.By (3.2),we deduce that

Consequently,passing to the limit asρ→0 in (3.6),we find a constantC>0 independent ofρsuch that

We are done once we show thatis uniformly bounded inn.By (2.7) and the boundedness of{un},we get that
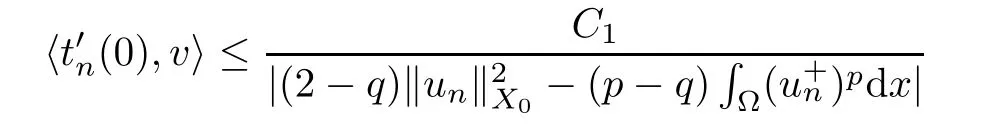
for some suitable constantC1>0.We only need to show thatis bounded away from zero.Arguing by contradiction,we assume that for a subsequence,which we still call{un},we have

By (3.5) and (3.7),we get thatis bounded away from zero.Thus,
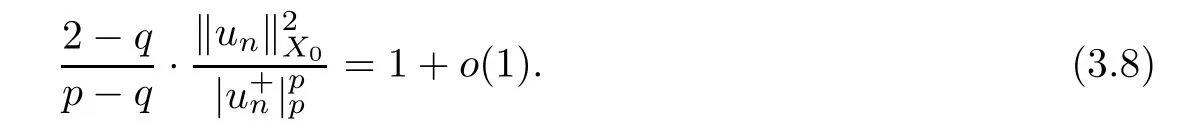
By (2.3),(2.4) and (3.7),we have that

Consequently,there exists a positive constantMsuch that

By (3.8)-(3.10),and the boundedness of{un},we have that

which is clearly impossible.We get

This completes the proof. □
Theorem 3.2Problem (1.1) has at least one positive ground state solutionuifλ∈(0,Λ).Moreover,u∈.
ProofBy Lemma 3.1,there exists a minimizing sequence{un}⊂NλforIλsuch that

asn→∞.Since,by Lemma 2.1,Iλis coercive on Nλ,we get that ‖un‖X0is bounded.Going,if necessary,to a subsequence,we can assume that


It follows thatIλ(u)=αλandun→ustrongly inX0.
We claim thatu∈.Assume,by contradiction,thatu∈.By Lemma 2.3,there exist positive numberssuch thatand
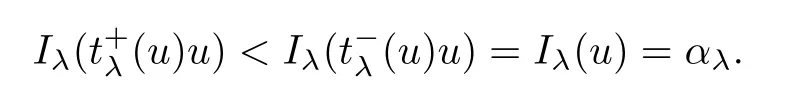
This is impossible,hence,u∈. □
4 Proof of Theorem 1.1
We define

Lemma 4.1Forλ∈(0,Λ),there exists asequence
ProofThe proof is slightly different than the proof of Lemma 3.1.In view of Lemma 2.5 we have thatis closed inX0,provided thatλ<Λ,and applying Ekeland’s variational principle[31]to the minimization problemwe have a minimizing sequence{un}⊂Nλwith the following properties:
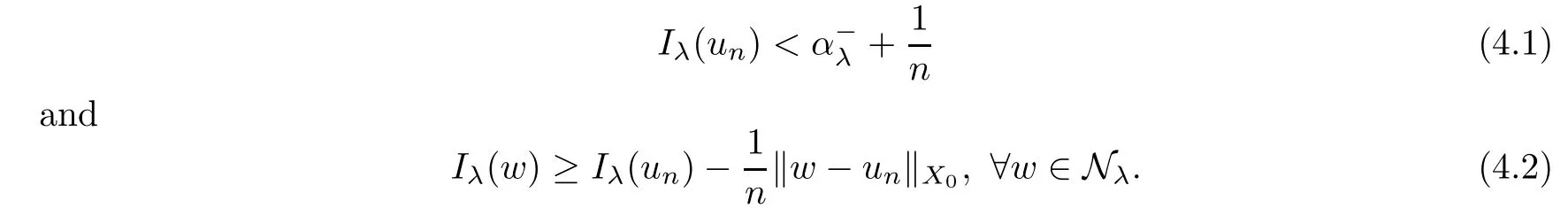
By (4.1) and Lemma 2.1,there exists a constantCλsuch that

Pickingw0∈,by Lemma 2.3 there existst(w0)>0 such thatt(w0)w0∈.By (2.4),we have that

By takingnlarge,from (4.1) and (4.4) we have that

At this point we can proceed as in the proof of Lemma 3.1 and use (4.3) and (4.5) to derive that(un)→0 asn→∞. □
Recall thatSpis defined as

It is well known from[24]that the in fimum in the formula above is attained at,where
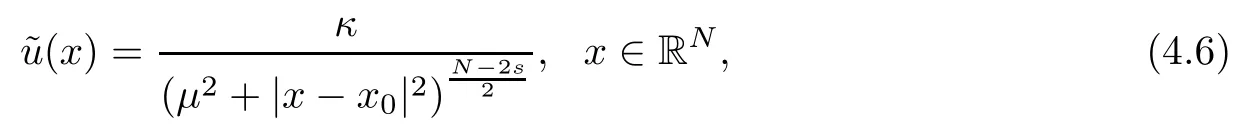
withκ∈R{0},μ>0 andx0∈RNas fixed constants.We suppose,for convenience,thatκ>0.Equivalently,the function¯udefined as
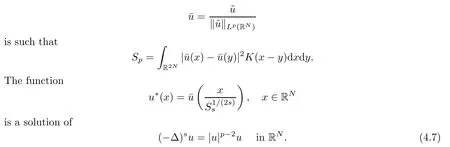
Now we consider the family of functionUε,defined as

for anyε>0.The functionUεis a solution of problem (4.7) and satisfies

Fixa∈Ω.Letη∈C∞be such that 0≤η≤1 in RN,η(x)=1 if|x-a|<ρ0/2;η(x)=0 if|x-a|≥ρ0,whereρ0>0 is small enough such that{x∈RN:|x-a|≤ρ0}⊂Ω.For everyε>0 we denote byuεthe following function:
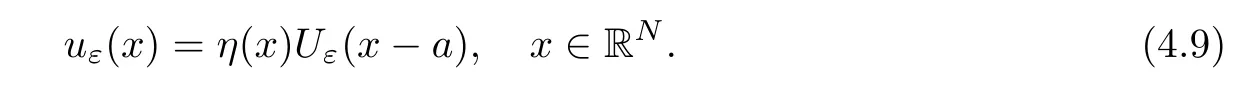
In what follows we suppose that,up to a translation,x0=0 in (4.6).From[24]we have the following estimates:

Proposition 4.2There existε0>0 such that,forε<ε0andλ∈(0,Λ),
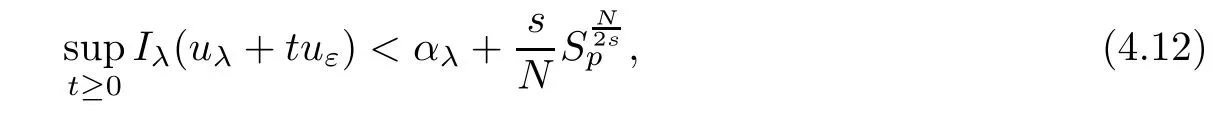
whereuλis the positive solution obtained in Theorem 3.2.
ProofSinceIλis continuous inX0anduεis uniformly bounded inX0,there existst1>0 such that,fort∈[0,t1],

Direct computation yields that

By (4.11),we have

forεsmall enough.Note that the last term in (4.13) satisfies

Thus,I(uλ+tuε)→-∞ast→∞uniformly inε.Consequently,there existst2>t1such thatfort≥t2.Then,we only need to verify the inequality

forεsmall enough.
From now on,we assume thatt∈[t1,t2].
There exists a constantC>0 such that
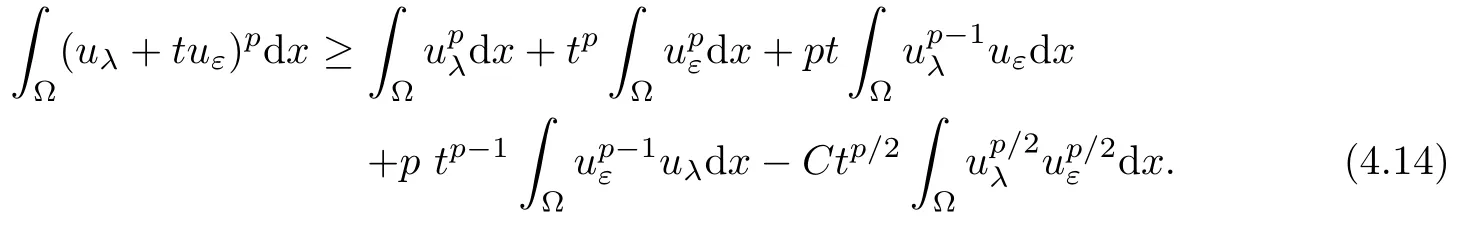
We have used the following inequality (see[32],for example):forr>2,there exists a constantCr(depending onr) such that

Using the fact thatuλis a positive solution of (1.1),(4.14),(4.10) and (4.11),we have that

Here we have used the elementary inequality (α+β)q≥αq+qαq-1β,∀α,β>0.
Now we estimate the third term in (4.15).There exists a constantC1>0 such thatuλ(x)≥C1for allx∈Bρ0/2(a).Then,

Direct computation yields that there exists a constantC2>0 independent ofεsuch that

By (4.15),(4.16) and (4.17),we have that
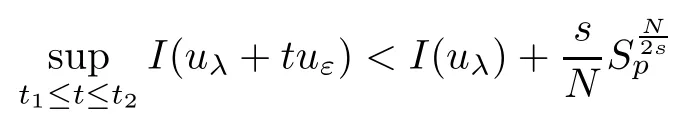
forεsmall enough. □
Define

Lemma 4.3Assume thatλ∈(0,Λ).We have that
(iii) there existstε>1 such thatuλ+tεuε∈A2;
(iv) there existssε∈(0,1) such that
Proof(i) Set

(iii) First,we claim that there exists a positive constantCsuch that

Assume,by contradiction,that there exists a sequence{tn}such thattn→+∞and+∞asn→∞,whereSince,by Lebesgue’s Dominated Convergence Theorem,we have that

asn→∞.Thus,

asn→∞,which is impossible,since,by Lemma 2.1,Iis bounded from below on Nλ.

Hence,we getuλ+tεuε∈A2.
(iv) Defineγ:[0,1]→R as

Note thatγ(s) is a continuous function ofs.Sinceγ(0)>1 andγ(1)<1,there existssε∈(0,1) such thatγ(sε)=1;that is,uλ+sεtεuε∈.
(v) By Proposition 4.2 and (iv),we have that□
Lemma 4.4Iλsatisfies the (PS)βcondition inX0for
ProofLet{un}be a (PS)βsequence forIλsuch that

Then,fornbig enough,we have that
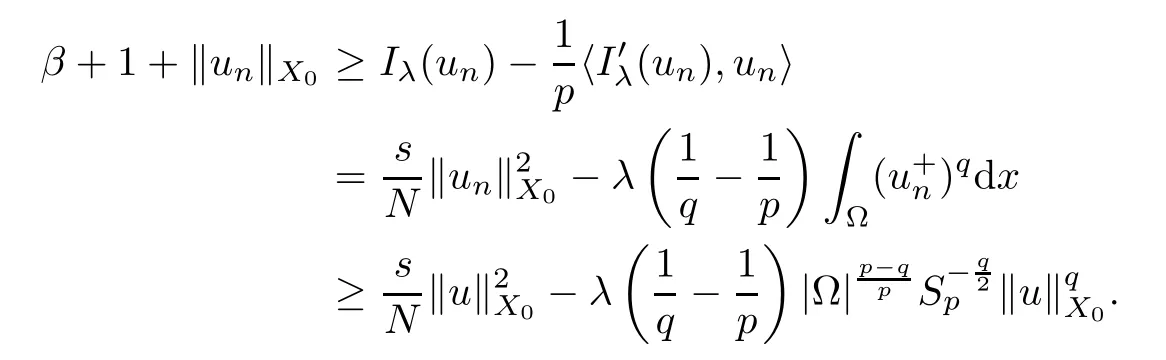
It follows that ‖un‖X0is bounded.Going,if necessary,to a subsequence,we can assume that

Setvn=un-u0.SinceX0is a Hilbert space,we have that

By Brezis-Lieb’s Lemma,we have that

By (4.20) and (4.21),we have that

By (4.18) and (4.19),we have that

Now,we assume that

By (1.3) and (4.25),we obtain that
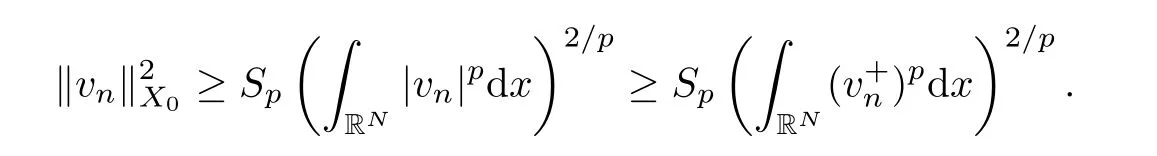
Passing to the limit,we have that
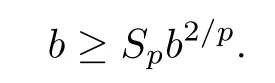
This implies thatb=0 or.Ifb=0,the proof is complete.Assume that.By (4.23) and (4.25),we have that

which implies a contradiction.Hence,b=0,that is,un→u0inX0asn→∞. □
Theorem 4.5For allλ∈(0,Λ) problem (1.1) admits at least one positive solution in
ProofBy Lemma 4.1 there exists asequence{un}⊂forIλ.SinceIλsatisfies the (PS)βcondition forby Lemma 4.4,andby Lemma 4.3,Iλhas at least one critical pointuin Nλforλ∈(0,Λ).By lemma 2.5,we have thatis closed inX0topology.Thusu∈. □
Proof of Theorem 1.1This is an immediate consequence of Theorems 3.2 and 4.5.
 Acta Mathematica Scientia(English Series)2022年3期
Acta Mathematica Scientia(English Series)2022年3期
- Acta Mathematica Scientia(English Series)的其它文章
- BOUNDEDNESS AND EXPONENTIAL STABILIZATION IN A PARABOLIC-ELLIPTIC KELLER–SEGEL MODEL WITH SIGNAL-DEPENDENT MOTILITIES FOR LOCAL SENSING CHEMOTAXIS*
- ABSOLUTE MONOTONICITY INVOLVING THE COMPLETE ELLIPTIC INTEGRALS OF THE FIRSTKIND WITH APPLICATIONS*
- THE ∂-LEMMA UNDER SURJECTIVE MAPS*
- PARAMETER ESTIMATION OF PATH-DEPENDENT MCKEAN-VLASOV STOCHASTIC DIFFERENTIAL EQUATIONS*
- GLOBAL INSTABILITY OF MULTI-DIMENSIONAL PLANE SHOCKS FOR ISOTHERMAL FLOW*
- THE SYSTEMS WITH ALMOST BANACH-MEAN EQUICONTINUITY FOR ABELIAN GROUP ACTIONS*
