QUASILINEAR EQUATIONS USING A LINKING STRUCTURE WITH CRITICAL NONLINEARITIES*

Edcarlos D.SILVA Jefferson S.SILVA

Federal University of Goi´as，Zip code 74001-970，Goi´as-GO，Brazil

E-mail:edcarlos@ufg.br;jeffersonsantos.mat@gmail.com

Abstract It is to establish existence of a weak solution for quasilinear elliptic problems assuming that the nonlinear term is critical.The potential V is bounded from below and above by positive constants.Because we are considering a critical term which interacts with higher eigenvalues for the linear problem，we need to apply a linking theorem.Notice that the lack of compactness，which comes from critical problems and the fact that we are working in the whole space，are some obstacles for us to ensure existence of solutions for quasilinear elliptic problems.The main feature in this article is to restore some compact results which are essential in variational methods.Recall that compactness conditions such as the Palais-Smale condition for the associated energy functional is not available in our setting.This difficulty is overcame by taking into account some fine estimates on the critical level for an auxiliary energy functional.

Key words Quasilinear Schrdinger equations;linking theorems;superlinear elliptic equations;critical nonlinearities;Bounded potentials

1 Introduction

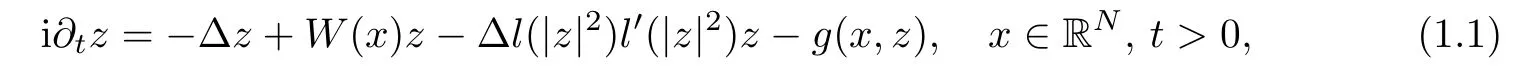
wherez∈C(R×RN，C)，W∈C(RN，R) is a potential，lis a suitable real function，andg∈C(RN×R，R) is a nonlinearity which have been accepted as a model in many physical settings.

It is worthwhile for us to describe different physical frameworks depending on the functionl.Indeed，depending on the nonlinear termgand the functionl，we can consider also several phenomena such as Bose-Einstein condensates，Bose-Fermi mixture as well as many others applications on nonlinear optics，plasma physics，super fluid films and quantum mechanics;see，for instance，[4，11，12].For more details we refer the interested reader to[3，5，23].Notice that this condition includes fluid mechanics，plasma physics and dissipative quantum mechanics case.On this subject，we refer the reader to[1，15，25，27，34，38].For example，assuming thatl(t)=1，we obtain the classical semilinear Schrdinger equation;see[2，7，14，29].Furthermore，for the functionl(t)=t，equation (1.1) led us to the fluid mechanics，plasma physics and dissipative quantum mechanics;see[11，13，17，24].Notice that our problem is motivated because of several results on the existence of weak solutions for problem (1.1) choosingl(t)=t.Hence we consider，in this article，l(t)=t.Since we are interested in solitary wave solutions，namely，we look for solutions with the special formz(t，x)=exp (-iEt)u(x)，withE∈R andz∈C(R×RN，C)，whereuis real function，we consider the following equation:

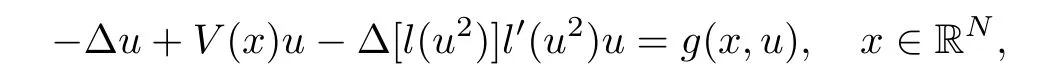
whereV=W-Eis the new potential.More specifically，we shall consider the existence of weak solutions to the following quasilinear elliptic problem:

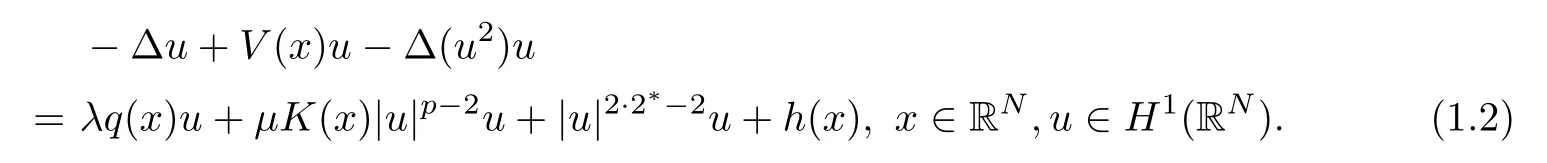
Throughout this work，we consider thatN≥3，4＜p＜2·2*，V，K∈C(RN，R)，q∈Lα(RN)，α＞N/2 andh∈L2N/(N+2)(RN).Moreover，we takeλ∈(λj，λj+1)，where the sequence (λj)j∈N⊂R denotes the eigenvalues for the associated linear problem andμ＞0 is a real parameter.Later on，we shall discuss some assumptions on the functionsV，q，Kandh.For an easy reference，we writeg(x，t)=λq(x)t+μK(x)|t|p-2t+|t|2·2*-2t，x∈RNandt∈R.

It is worthwhile to mention that problem (1.2) exhibits many difficulties.First，looking for standing wave solutions to problem (1.1)，we need to consider the following quasilinear elliptic problem:

It is well known that problem (1.3) can not be considered directly using variational methods.More precisely，for quasilinear elliptic problems there does not exist any functional ofC1class associated to (1.3).The second difficulty appears because the potentialVis bounded.Hence，any compact embedding from Sobolev spaces to the Lebesque space is not available.Furthermore，the nonlinearitygadmits a critical behavior which is also asymptotically linear at the origin.In fact，ghas an interaction with the linear because of the termλq(x)u.In order to get our main result，using a changing of variablefintroduced by[6，18]，we can consider the following semilinear elliptic problem:

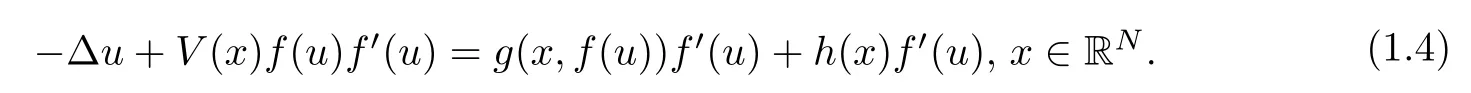
Now，looking for problem (1.4)，we obtain an associated energy functionalJμwhich is inC1class.Moreover，we observe that any critical point forJμis a weak solution to the elliptic problem (1.4).

To the best of our knowledge，up to now，the results do not exist on the existence of solutions for critical quasilinear elliptic problems，where the potentialVis bounded and the nonlinear termginteracts with higher eigenvalues for the associated linear problem.Notice thatu=0 is not anymore a local minimum for the energy functionalJμ.Assuming thatu=0 is a local minimum point for the associated energy functionalJμ，several results concerning existence，multiplicity and asymptotic behavior of solutions for quasilinear Schrdinger equations have been considered.On this subject，we refer the reader to[6，8–10，18–21].In view of our assumptions，we consider the following behavior forgat the origin and at infinity:

Recall that the last limits holds for some functionk∈Lα(RN) withα＞N/2.Hence，we considergasymptotically linear at the origin and superlinear at infinity.

In this article，the aim is to consider quasilinear elliptic problems，where the nonlinearityghas an interaction with high eigenvalues. It is important to point out that under our assumptions，u=0 is not anymore a local minimum for the associate energy functional.In this way，by applying a linking theorem and taking into account the potentialsqandV，we shall prove existence of solutions for problem (1.2).Recall also that the quasilinear term Δ(u2)ugive us serious difficulties in order to prove the geometric assumptions for the linking theorem.Furthermore，the nonlinearityghas critical growth，which implies that compactness conditions are not available in general.In order to overcame these difficulties，we prove thatJμgoes to zero asμ→∞，whereJμis the energy functional for problem (1.2);see Section 3 ahead.

1.1 Assumptions and statement of main results

In this article，we consider existence of weak solutions for quasilinear elliptic equations，where the nonlinearityginteracts with higher eigenvalues for the associated linear problem.For our main result，we need to consider some extras hypotheses onV，q，K.Precisely，we assume the following hypothesis:

(V1)Vis continuous，1-periodic for eachxiwith 1≤i≤N.Assume also that there exist positive constantsV0，V∞such thatV0≤V(x)≤V∞for allx∈RN.

For the potentialq，we consider the following condition:

(q1)q∈Lα(RN) for someα＞N/2 andq(x)＞0，a.e.x∈RN.Assume also thatq(x)≤cq1(|x|)，x∈RN，c＞0，whereq1is radial andr→q1(r)αrN-1∈L1(R)，r=|x|for eachx∈RN.

For the potentialK，we shall consider the following assumption:

(K1)Kis continuous，1-periodic for eachxiwith 1≤i≤N.Assume also that there exists a positive constantk0such thatK(x)≥k0for allx∈RN.

For the non-homogeneous functionh，we assume the following condition:

(h1)h∈L2N/(N+2)(RN).

It is important to emphasize that the weighted eigenvalue problem，given by

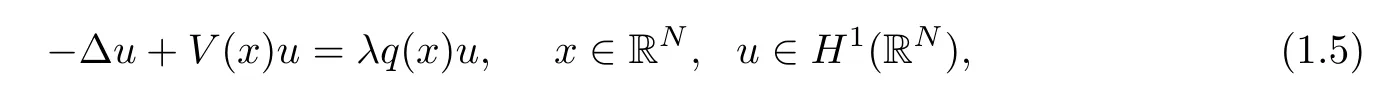
admits a sequence of eigenvalues (λj) such that 0＜λ1≤λ2≤...≤λj...andλj→∞asj→∞.This can be done by using the spectral theory for self-adjoint compact operators;see Section 2 ahead.The key point here is to use hypothesis (q1) together with the fact thatVis bounded from below and above.Hence，the eigenvalues for problem (1.5) can be characterized using standard procedures.In this way，in this article we shall consider problem (1.2) takingλ∈(λj，λj+1);that is，we consider the nonlinearityginteracting with higher eigenvalues.

It is important to stress that a functionuis said to be a weak solution for the elliptic problem (1.2) provided that

holds for allφ∈(RN)，whereg(x，t)=λq(x)t+μK(x)|t|p-2t+|t|2·2*-2t，x∈RN，t∈R.Under our assumptions，takingh≡0 it follows thatu≡0 is the trivial solution for problem (1.2).In this case，we need to consider existence of nontrivial solutions for problem (1.2).Using some fine estimates，we ensure that the energy functional associated to problem (1.2) admits the linking structure even in the caseh≡0.In this way，we prove that the associated critical energy level given by the Liking Theorem，denoted bycμ，goes to zero asμ→∞.Hence，by using the last assertion，we shall prove that problem (1.2) admits also a nontrivial solution forh≡0.

Now，we are in position to state the main result for this article.Namely，in order to control the energy level for the associate energy functional，by using some fine estimates we can prove the following result:

Theorem 1.1Assume that (V1)，(q1)，(K1) and (h1) hold.Suppose also thatλ∈(λj，λj+1) holds for somej≥1.Then there existμ0＞0 and∈＞0 such that problem (1.2) has at least one weak solution for eachh0 provided that 0＜‖h‖2N/(N+2)＜∈andμ＞μ0.Furthermore，problem (1.2) has at least one nontrivial weak solution forh≡0 andμ＞μ0.

As was told before，the functionalJμdoes not admitsu=0 as a local minimum.For the related results，we refer the interested reader to[22，26，34–37]，where the quasilinear elliptic problems were treated with subcritical and critical assumptions on the nonlinear termg，respectively.In this article，by using the fact thatVis bounded，the embedding for Sobolev spaces into Lebesgue spaces are only continuous.Notice that for our main problem，the nonlinear termghas an asymptotically-superlinear function together with a non-homogeneous functionhwhich can be the zero function.Furthermore，by using the fact thatghas a critical growth，we need also to control the energy level for the associate energy functional.Namely，we prove that the critical level for the associate functionalJμgoes to zero asμ→∞.Therefore，our main result complements the early results by considering existence of solutions for quasilinear elliptic problems with bounded potentials for critical nonlinearities.Recall also that once more the lack of compactness bring us a difficulty to apply variational methods.

Remark 1.2Notice that constant potentialsVis allowed;that is，the potentialV(x)=V0=V∞＞0 for eachx∈RNsatisfies our hypotheses.In the literature，this case is named as the autonomous case.Recall that the potentialqis not periodic. Hence，the energy functional associated to elliptic problem (1.1) is not invariant under translations even for constant potentialsV.In order to overcome this difficulty，we consider hypothesis (q1) to show thatJμcan be controlled at infinity.

Now，we are stay in position to consider some remarks for our assumptions.

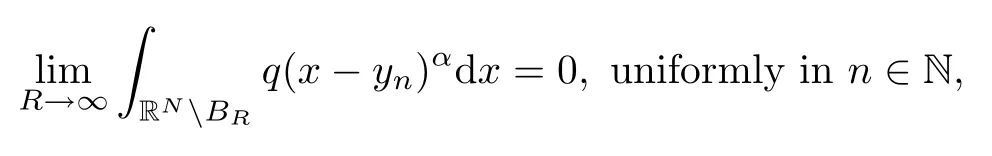
Remark 1.3In this article，we can consider also the following general condition:() Suppose thatq∈Lα(RN) for someα＞N/2 andq(x)＞0，a.e.x∈RN.Assume also that where (yn)n∈N∈RNsatisfies|yn|→∞asn→∞.Notice that hypothesis (q1) implies that () is verified.Indeed，after a change of variables and using the coarea formula，we observe that

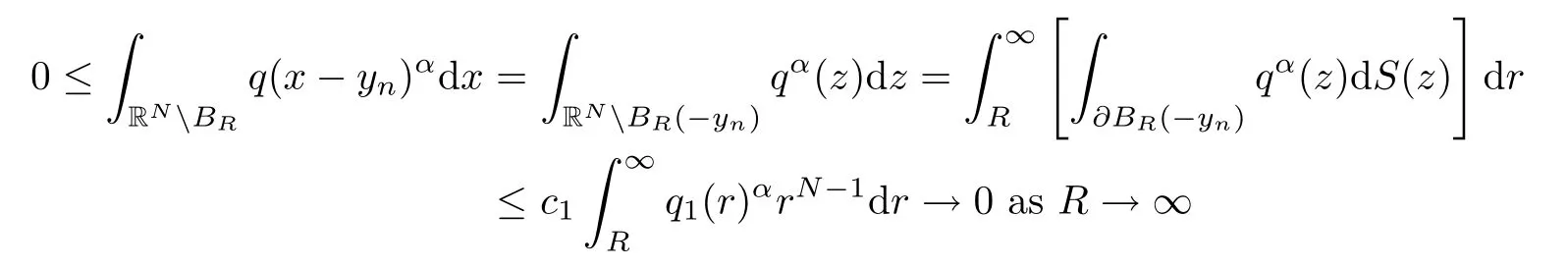
holds true for some constantc1＞0.This can be done by applying Lebesgue Convergence Theorem together withq1(r)αrN-1∈L1(R).Hence，our hypothesis (～q1) can be used to get weak solutions for our main problem.

Now，we consider some examples as prototypes for the functionsV，qandK.

Example 1.4As was told before，we can putV(x)=V0for allx∈RNwithV0＞0.In the same way，we can also consider the potentialV(x)=V0+sin2(2πx1) sin2(2πx2)...sin2(2πxN)，whereV0＞0.This function satisfies assumptionAnalogously，we takeK(x)=k0+sin2(2πx1) sin2(2πx2)...sin2(2πxN)，wherek0＞0.Therefore，Kis a positive function.Notice also thatKis 1-periodic for eachxiwith 1≤i≤N.As a consequence，Ksatisfies hypothesis (K1) for anyk0＞0.Now，for the potentialq，we put

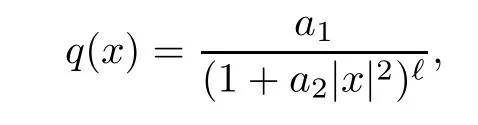
wherea1＞0 anda2＞0.It is not hard to verify thatqis inLα(RN) for eachα＞N/(2ℓ) andqis radial.Hence，by using the coarea formula，qsatisfies hypothesis (q1).

Example 1.5Now，we consider，as example，the following potentialV(x)=asin2(2πx1) sin2(2πx2)...sin2(2πxN)，wherea＞1. For this example，we obtainV0=Similarly，we consider the functionK(x)=k0-sin2(2πx1) sin2(2πx2)...sin2(2πxN)，wherek0＞1. Hence，the functionsVandKare positive and 1-periodic for eachxiwith 1≤i≤N.As a consequence，VandKsatisfies hypotheses (V1) and (K1)，respectively.In the same way，we consider

wherea＞0 andℓ＞0.Notice thatq∈Lα(RN) for anyα＞N/2.Now，using the same ideas discussed in the previous example，the functionqsatisfies hypothesis (q1).

1.2 Outline

The remainder of this article is organized as follows:in the forthcoming Section 2，we consider the variational framework for the quasilinear elliptic problem (1.2).Section 3 is devoted to the proof of linking geometry for the associated energy functional together with the proof of the boundedness for each Palais-Smale sequence.In Section 4，we give the proof of our main result.

1.3 Notation

Let us introduce the following basic notations used in this article:

·on(1) denotes a sequence which converges to 0 asn→∞;

·The norm inLq(RN) andL∞(RN) will be denoted，respectively，by ‖·‖qand ‖·‖∞withq∈[1，∞);

·The usual norm inE=H1(RN) is denoted by ‖·‖♯;

·For any measurable functionw:RN→R，we denote[w0]:={x∈RN:w(x)0}.We also denote[w≤k]:={x∈RN:w(x)≤k}for anyk∈R.Similarly，we consider[w≥k];

·The Lebesgue measure for any measurable A is denote by|A|.

2 The Variational Framework

Throughout this article，the working space is given by the Sobolev spaceE=H1(RN) endowed with norm

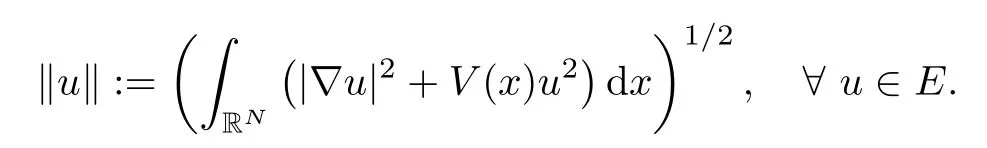
This norm is equivalent to the usual norm inEdefined by

The norm ‖·‖ is induced by the inner product

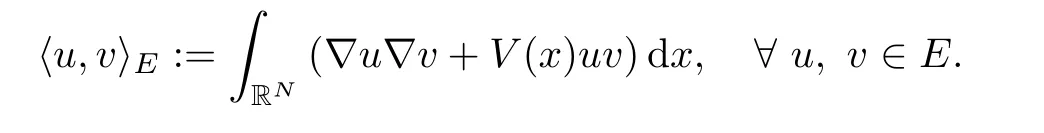
For our purposes，we need to consider a Linking Theorem which is useful for us to get our main result in this article.LetEbe a Banach space endowed with the norm ‖·‖.Consider a functionalJ:E→R ofC1class.Recall that a sequence (un)n∈N∈Eis said to be a Palais-Smale sequence at the levelc∈R，in short (PS)csequence，wheneverJ(un)→candJ′(un)→0 asn→∞.The functionalJsatisfies the Palais-Smale condition at the levelc∈R，in short (PS)ccondition，whenever any (PS)csequence possesses a convergent subsequence.WhenJsatisfies the (PS)ccondition at any levelc∈R，we say purely thatJsatisfies the (PS) condition.In this article，we shall prove that the energy functional associated to our main problem satisfies a linking geometry introduced in[30，31].On this subject，we refer the interested reader to the important works[28，32，33].Here，we shall consider the following Linking Theorem:

One by one, in the early morning darkness, my eighth-graders and I boarded the bus. When Robbie Brown got on, he was holding a four-inch pot with a white hyacinth. The delicate flowers were in full bloom. There was a small American flag stuck in the soil. Everyone asked Robbie what the flower was for. All he d say was that he was on a mission.

Theorem 2.1(Linking Theorem[30]) LetE=E1⊕E2be a real Banach space，whereE1is finite dimensional.Suppose thatJ∈C1(E，R) satisfy the following geometric conditions:

(J1)J(v)＜σfor allv∈E1，whereσ∈R;

(J2) There existρ＞0 such thatJ(v)≥σ，∀v∈∂Bρ(0)∩E2;

(J3) There existe∈∂B1(0)∩E2andβR∈R such that

Assume also thatβR/Rγ+1→0 asR→∞，for someγ≥0.Then，there exists a sequence (vn)n∈N⊂Esuch thatJ(vn)→candJ′(vn)→0.Recall that the minimax levelc＞0 is given

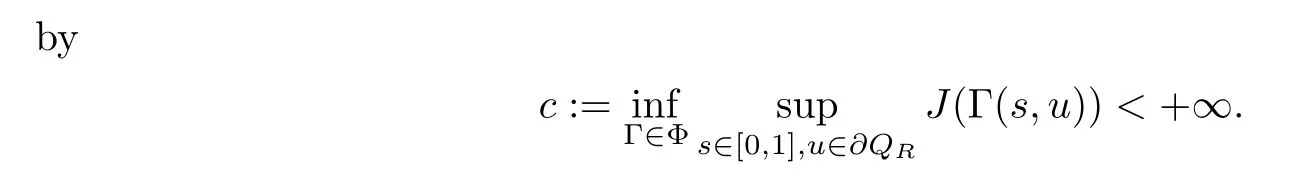
Notice that Γ∈C([0，1]×E，E) satisfies some assumptions (see[30]).

At this stage，we writeE=E1⊕E2，whereE1:=span{φ1，...，φj}andE2:=E⊥1.The functionsφkare eigenfunctions of the linear eigenvalue problem (1.5) associated to eigenvalueλkfor eachk≥1，respectively.Notice that subspacesE1andE2are orthogonal and dim (E1)＜∞.The first eigenvalueλ1is characterized by

More generally，for eachk≥2，the eigenvalueλkis characterized by

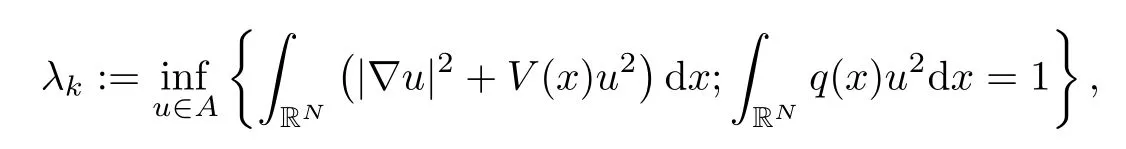
whereA={u∈E{0};〈u，φi〉E=0，∀i∈{1，2，...，k-1}}.In the same way，we shall consider the weighted Lebesgue spaceL2（RN，q），given by

whereq∈Lα(RN) for someα＞N/2，q(x)＞0 a.e.x∈RN.Notice also thatL2（RN，q）is a Banach space endowed with the natural norm

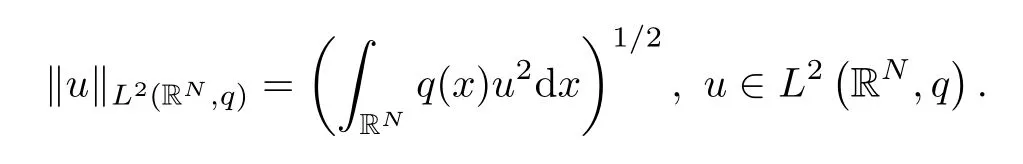
Now，we shall give some compact embedding for Sobolev spacesEinto weighted Lebesgue spaces.In order to do that，we need to discuss some properties forL2（RN，q）.Firstly，we consider an auxiliary result given in[37]，which can be rewritten in the following form:

Lemma 2.2(Compact embedding[37]) Letq∈Lα(RN) be a fixed function withα＞N/2.Then the embedding ofEintoL2（RN，q）is compact.

Under these conditions，we shall consider some inequalities for the eigenvalue problem (1.5).These inequalities are powerful tools in order to provide the behavior of our energy functional at the origin and at infinity.More precisely，we consider the following result:

Lemma 2.3Suppose that (V1) and (q1) holds.Then we obtain the following inequalities:

(i) For allu∈E，there holds

(ii) For allu∈E1，there holds

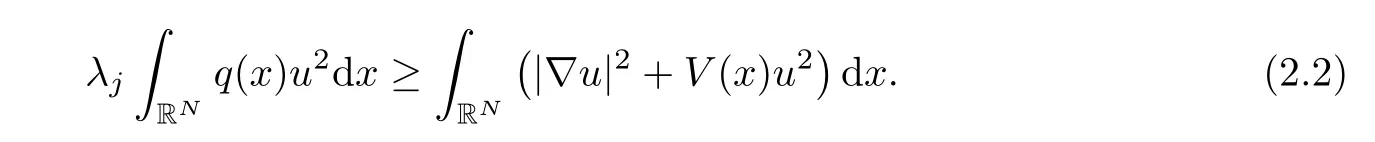
(iii) For allu∈E2，there holds

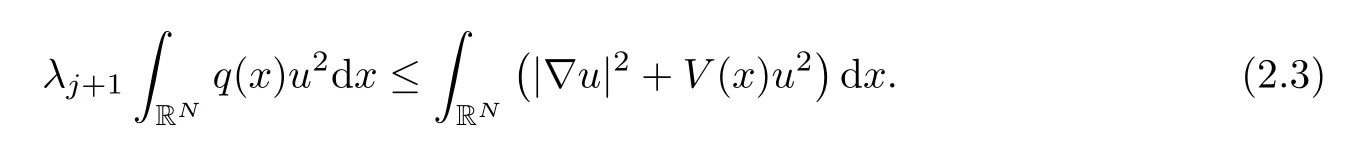
ProofThe proof follows using the spectral theory for compact operators taking into account the compact embedding given by Lemma 2.2.We omit the details. □

It is important to emphasize that problem (1.2) is formally the Euler-Lagrange equation associated to the functional

It is worthwhile to mention that any critical pointsu∈E∩L∞(RN) for the functionalIμare weak solutions to problem (1.2).However，the nonlinear termRRNu2|∇u|2dxis not well defined in the wholeE.More specifically，there existsu∈Ein such way that the last integral is infinity.Hence，following some ideas introduced in[6，18]，we reformulate problem (1.2) by using the change of variablef:given by

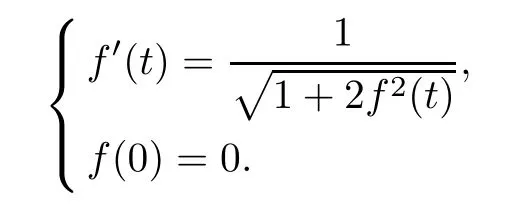
Now，we present the main properties of the functionfgiven just above whose proof can be checked in[6，9，10，37].Recall that these conditions are crucial in this article allowing control for the energy functional at infinity and at the origin.More specifically，we consider the following result:

Lemma 2.4The functionf:R→R satisfies the following properties:

Now，by using the change of variablesu=f(v) in the functional given in (2.4)，we consider the auxiliary functional

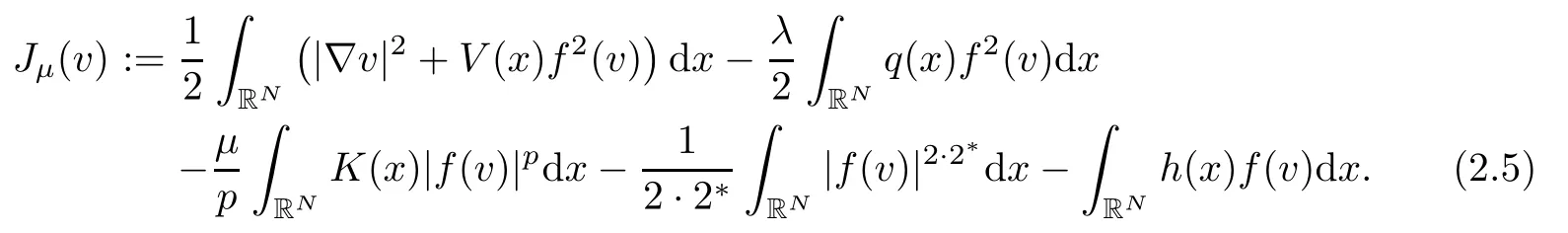
Notice that the functionalJμis well defined in the usual Sobolev spaceEand it isC1class.In fact，by using hypotheses (V1)，(q1)，(K1)，(h1) and Lemma 2.4，we deduce thatJμ∈C1(E，R).

Hence，any critical points of the functionalJμcorrespond precisely to the weak solutions for the following semilinear elliptic problem:

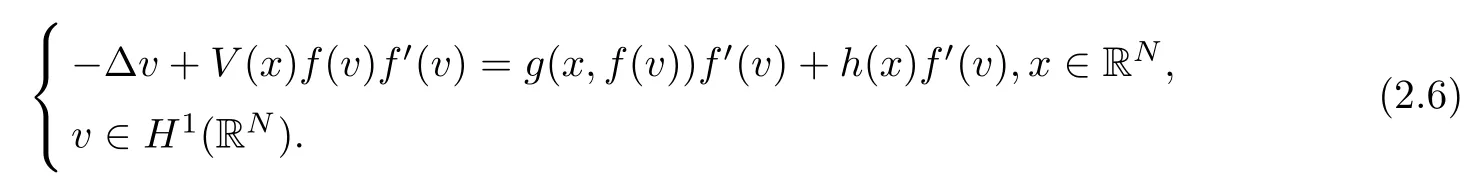
In view of the last assertion，we need to ensure existence of critical pointsvfor the associated energy functionalJμ.It is easy to verify thatu=f(v)∈E∩L∞(RN) is a weak solution for (1.2) provided thatv∈E∩L∞(RN) is a weak solution to problem (2.6).Hence，our purpose is sufficient to guarantee existence of critical points for the auxiliary functionalJμ.

Remark 2.5Notice that any weak solutionvfor problem (2.6) is inL∞(RN).This can be done by using Bresis-Kato Theorem to show thatv∈Ls(RN) for eachs∈[2，∞].More precisely，for each weak solutionsvof (2.6)，we can use standard elliptic regularity theory such as the Bresis-Kato Theorem together withLpestimates to prove thatholds for someγ∈(0，1).Moreover，taking into account hypothesis (q1) withα＞N，we know thatholds for someγ∈(0，1).Furthermore，assuming that the functionsV，qandgare locally Hlder continuous，it follows from Schauder theory thatholds for someγ∈(0，1);see[25].The same conclusion discussed here is also applied for any weak solution for the linear weighted problem (1.5).In particular，any weak solution for (1.5) is inL∞(RN).

3 The Linking Structure

In this section，we shall prove the linking structure for the energy functionalJμgiven in (2.5).The basic idea is to guarantee thatJμhas the linking geometry described in Theorem 2.1.Furthermore，we recover some compactness properties required in variational methods.Firstly，we consider the following result:

Proposition 3.1Suppose that (V1)，(q1)，(K1) and (h1) hold. Assume also thatλ∈(λj，λj+1) for somej≥1.Then there existρ，σ＞0 and∈1＞0 such thatJμ(v)≥σhold for allv∈∂Bρ∩E2provided that ‖h‖2N/(N+2)＜∈1.

ProofHere，we consider the auxiliary functional

Indeed，arguing by contradiction，choosing=1/n，we find a sequence (vn)n∈N⊂E2satisfying ‖vn‖=1/nin such way that

The sequence (vn)n∈Nsatisfiesvn→0 inE.Note that the working spaceEis continuously embedded intoLs(RN) for anys∈[2，2*].As a consequence，we obtain thatvn→0 inLs(RN) for eachs∈[2，2*].Furthermore，by using (3.4)，we deduce that

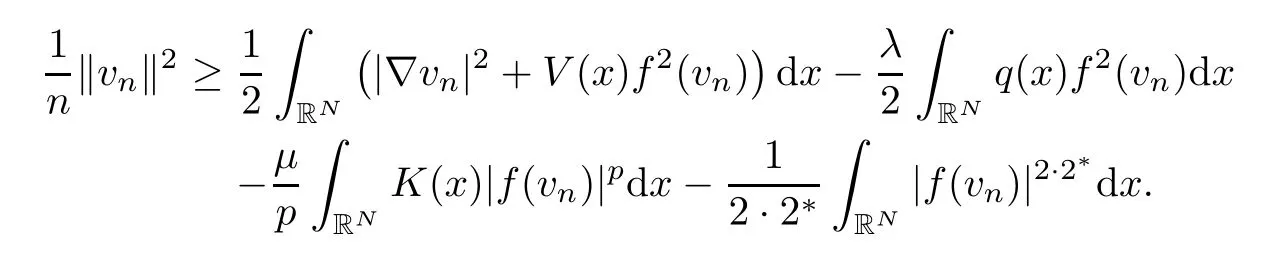
Define the normalized sequencewn=vn/‖vn‖.Under these conditions，up to a subsequence，we see thatwn⇀wweakly inE2，wn→wstrongly inandwn(x)→w(x)，a.e.in RN，hold true for any 1≤s＜2*.From now on，using the last estimate and (K1)，we see also that

Hence，the last estimate says that

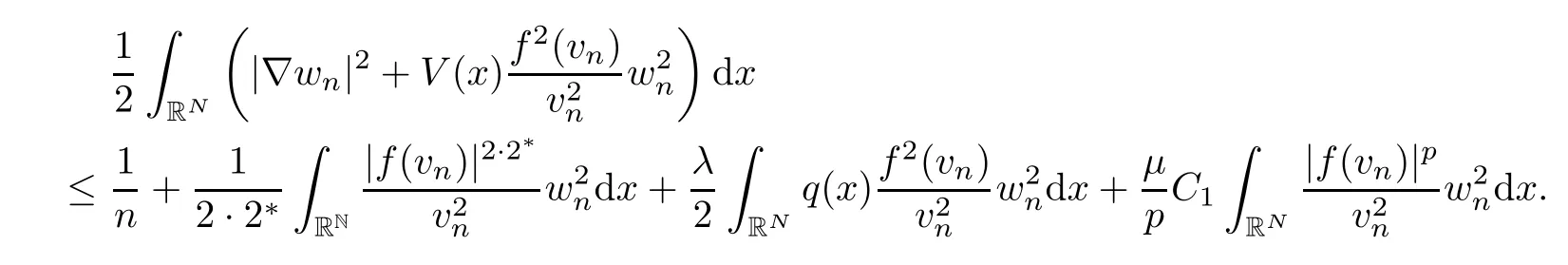
Now，we claim that

In fact，using the fact that 4＜l≤2·2*，we observe that Lemma 2.4(f7) implies that

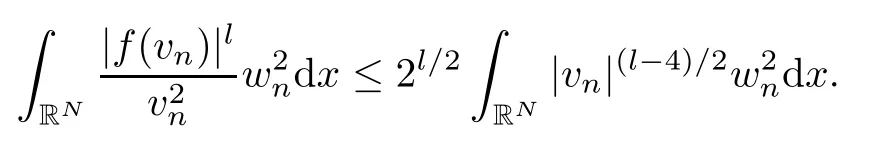
Notice also that|vn|(l-4)/2∈Ls(RN) fors=l/(l-4)＞1.It follows from Hlder’s inequality that

We here use the fact that (wn)n∈Nis bounded andvn→0 inLs(RN) for anys∈[2，2*].This finishes the proof of the claim given in (3.5).As a consequence，using Lemma 2.4(f3)，we get

According to Lemma 2.3 and using the fact that the (wn)n∈Nare normalized，we infer also that

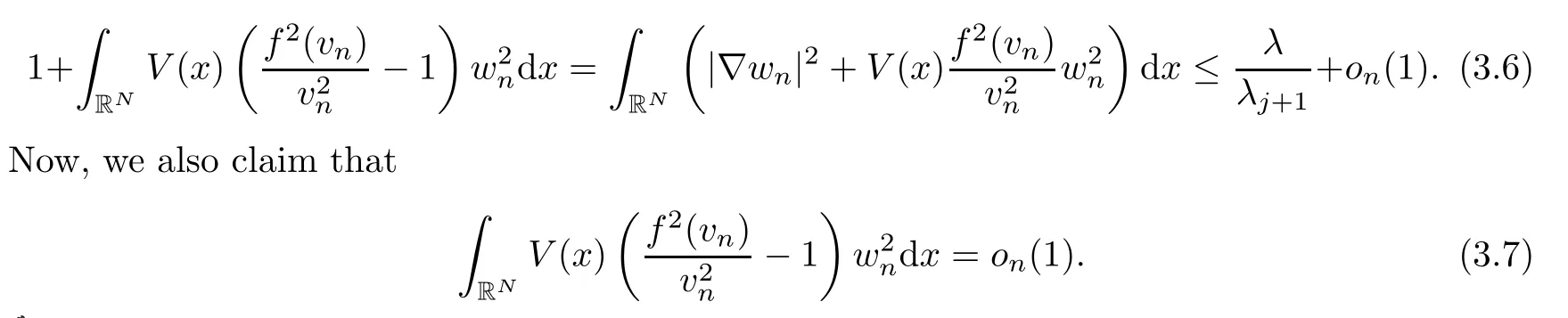
Assuming the claim just above and using (3.6)，we obtain thatλ≥λj+1.This is a contradiction，proving that (3.3) is now verified.It remains to prove claim (3.7).In order to do that，we chooseδ1＞0 and write

whereAn:={x∈RN||vn(x)|≤δ1}andBn:={x∈RN||vn(x)|＞δ1}.Now，we show that the integrals on the right hand side in identity just above goes to zero asn→∞.Firstly，we observe that|Bn|=on(1).Indeed，using the fact thatvn→0 inL2(RN)，we get

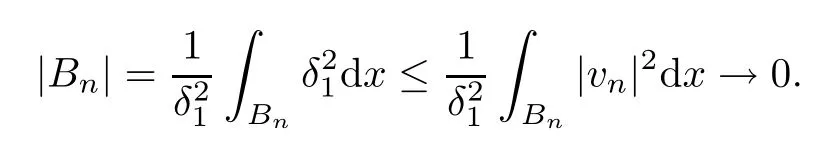
Thus，using (V1) and Lemma 2.4(f3)，the integral inBnis estimated as follows:

Now，choosingr=2*/2，the Hlder’s inequality implies that

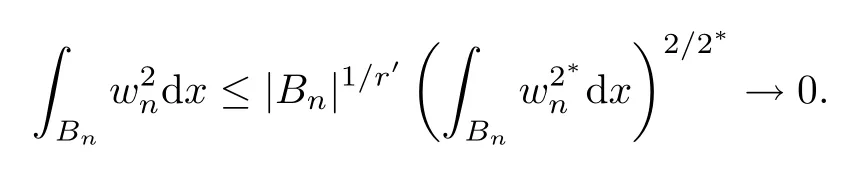
It follows from the last estimates that

Now，we consider the integral over the setAn.In order to do that，?using Le?mma 2.4(f4)，we observe that for each∈＞0，there existsδ＞0 satisfying the estimateδ.As a consequence，takingδ1=δ，we infer that

Now，using the fact thatEis continuously embedded intoL2(RN)，we have that there exists a constantC＞0 such that

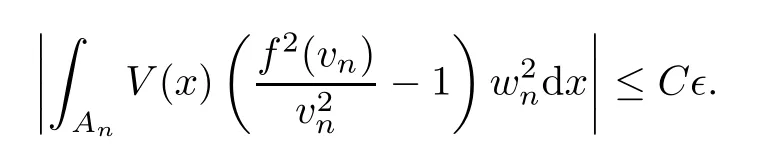
Putting all these estimates together，it follows from (3.8) that

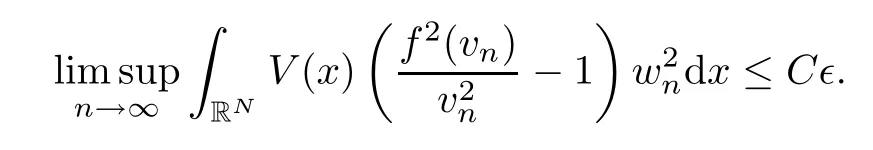
Hence，as∈＞0 is arbitrary，we finish the proof of claim (3.7).As a consequence，for allv∈E2with ‖v‖≤it follows from (3.2) thatFurthermore，using Lemma 2.4(f3)，(h1) and Hlder’s inequality，we also infer thatJμ(v)≥.Using the embeddingD1，2(RN) intoL2*(RN)，we see also thatJμ(v)≥‖v‖2-S-1‖h‖2N/(N+2)‖v‖，whereS＞0.Now，for eachv∈Esuch that ‖v‖=，we obtain from the last estimate that

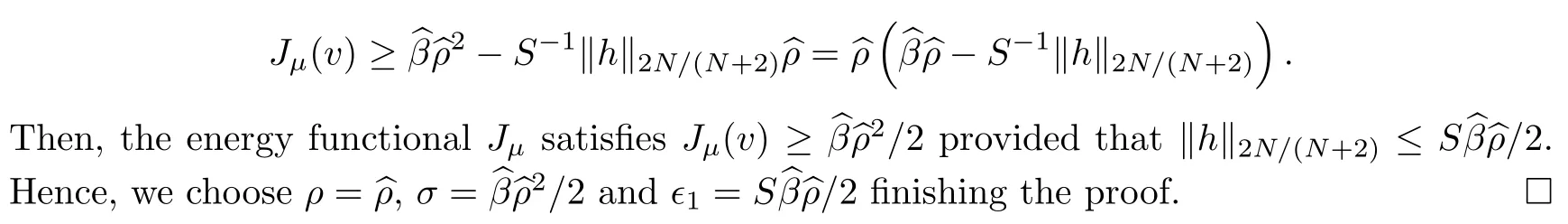
Proposition 3.2Suppose that (V1)，(q1)，(K1) and (h1) hold. Assume also thatλ∈(λj，λj+1) holds for somej≥1.Then，there existμ1∈R and∈2＞0 such thatJμ(v)＜σfor allv∈E1provided thatμ＞μ1and ‖h‖2N/(N+2)＜∈2，whereσwas defined in Proposition 3.1.

ProofAs previously defined in the proof of the previous proposition，we also consider the auxiliary functionalgiven in (3.1).Now，we claim that there existsθ＞0 such that

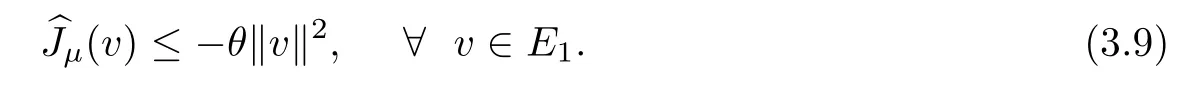
One more time，the proof for this claim follows arguing by contradiction.Then，choosingθ=1/n，we obtain a sequence (vn)n∈Nsatisfyingn∈N.Now，we split the proof into three cases.Namely，we consider the following cases:

Case 1.‖vn‖≤1/nfor alln∈N;that is，vn→0 inE1asn→∞;

Case 2.Up to a subsequence，‖vn‖→+∞asn→∞;

Case 3.There existδ＞0 andM＞0 in such way thatδ≤‖vn‖≤M，for alln∈N.

At this stage，we shall prove that each case just above is impossible.For Case 1，sincevn→0 inE，we deduce that

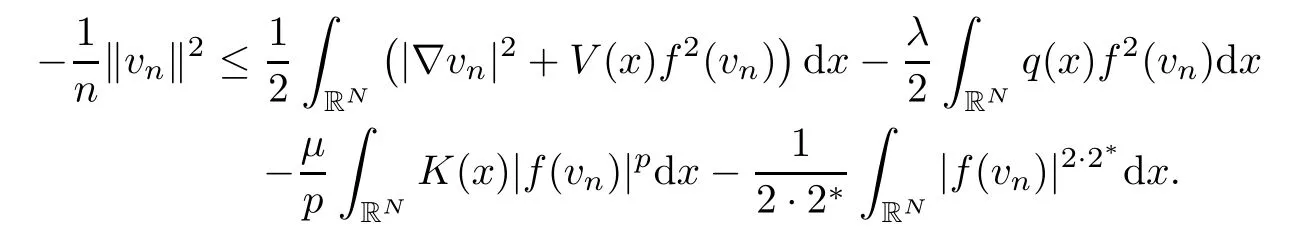
Using the condition (K1)，we see that

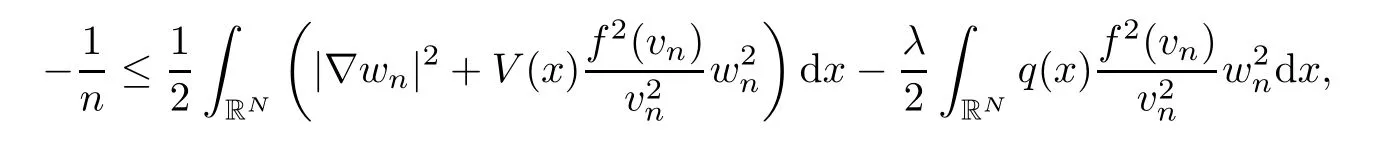
where we defined the normalized sequencewn=vn/‖vn‖.Taking into account thatE1is finite dimensional，wn→winE1andw0.Applying Lemma 2.4(f3)，we also see that

Sincewis nonzero，using the strong convergence and the embeddingEinto the Lebesgue spacesLs(RN) for alls∈[2，2*]，it follows from Lemma 2.4(f4) and Lebesgue Dominated Convergence Theorem that

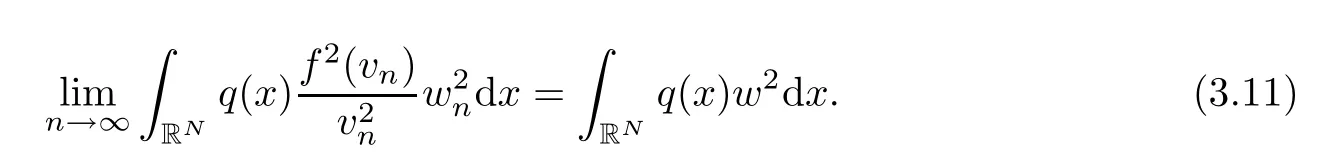
Taking the limit in (3.10) and using (3.11)，we infer also thatλRNq(x)w2dx≤1.According to Lemma 2.3 and using ‖w‖=1，we conclude thatλ≤λj.The last inequality is an absurd proving that Case 1 does not occur.

Now，we consider Case 2.Hence，up to a subsequence，we have ‖vn‖→∞asn→∞.Define the normalized sequencewn=vn/‖vn‖.Moreover，we observe thatwn→wstrongly inE1，w0，wn→wstrongly inLs(RN)，wn(x)→w(x)，a.e.in RN，|wn(x)|≤hs(x)，hs∈Ls(RN)，holds true for any 2≤s≤2*.Using the same ideas discussed in the proof of Case 1，we obtain the following estimates:

Taking into account hypotheses (q1)，(K1) and by Lemma 2.4(f3)，we also get

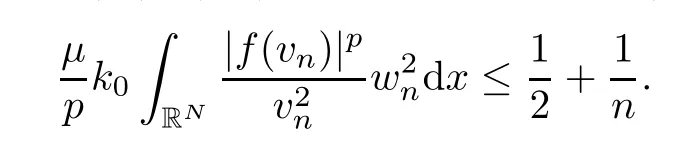
At this stage，we observe that|[w0]|＞0 with[w0]={x∈RN|w(x)0}.Therefore，we obtain|vn(x)|→+∞a.e.in[w0]asn→∞.As a consequence，applying the Fatou’s Lemma and using Lemma 2.4(f10)，we obtain a contradiction proving that Case 2 is impossible.

It remains to discard Case 3.For this case，up to a subsequence，there existsv∈E1in such way thatvn→vstrongly inE1，δ≤‖v‖≤M，vn→vstrongly inLs(RN)，vn(x)→v(x)，a.e.in RN，and|vn(x)|≤hs(x)，hs∈Ls(RN)，hold true for any 2≤s≤2*.Using the same ideas discussed in the proof of Case 1，we obtain that

wherewn=vn/‖vn‖.Using Lemma 2.4(f3) and hypotheses (q1) and (K1) one more time，we deduce that

Taking the limit in (3.12) and applying the Lebesgue Dominated Convergence Theorem，we infer that

Asδ≤‖v‖≤M，estimate (3.13) can be rewritten in the following form:

wherew=v/‖v‖.As dim (E1)＜∞，there exist positive constantsC1，C2in such way thatC1‖v‖∞≤‖v‖≤C2‖v‖∞，v∈E.Using Lemma 2.4，we observe thatf(t)/tis decreasing for allt＞0.Therefore，we get

Proposition 3.3Suppose that (V1)，(q1)，(K1) and (h1) hold. LetQbe a finite dimensional subspace ofE.Then there existsR＞0，depending on the dim (Q)，in such way thatJμ(v)≤0 for allv∈Qwith ‖v‖≥R.

ProofThe proof follows arguing by contradiction.Assume that there exists a sequence (vn)n∈Nsuch that ‖vn‖＞nandJμ(vn)＞0 for alln∈N.As a consequence，we see that

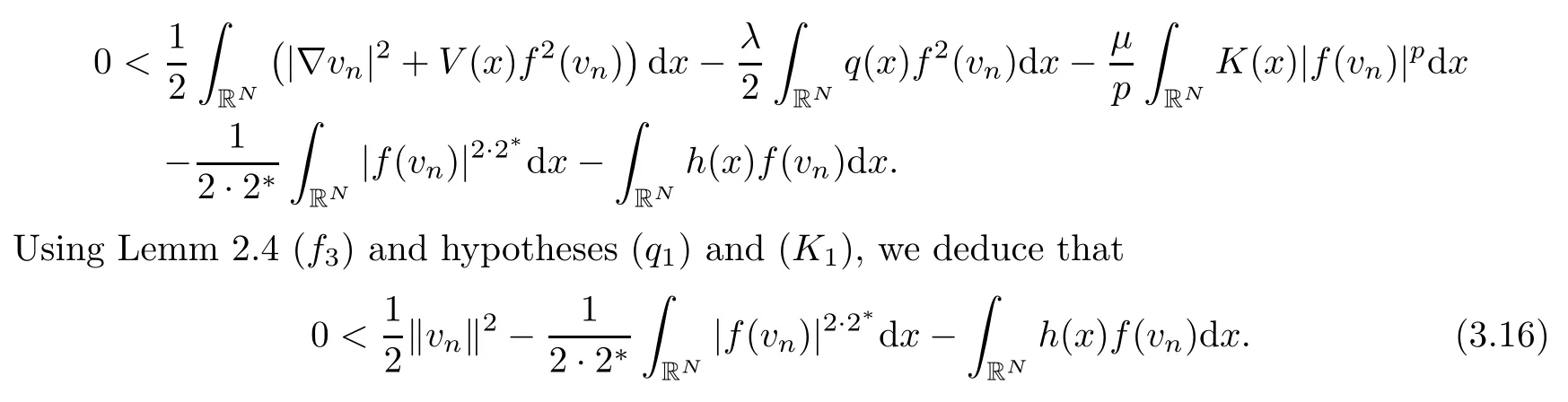
Furthermore，using conditions (h1)，Lemma 2.4(f3)，Hlder’s inequality and the embedding ofD1，2(RN) intoL2*(RN)，there exists a positive constantCin such way that≤C‖vn‖.It follows from (3.16)，together with previous estimate，that

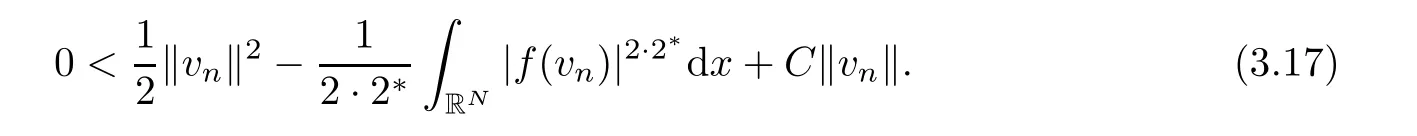
Notice that the sequence (vn)n∈Nsatisfies ‖vn‖→∞asn→∞.Thus，define the normalized sequencewn=vn/‖vn‖ for alln∈N.It follows also thatwn→w0 strongly inQ，wn→wstrongly inLs(RN)，wn(x)→w(x)，a.e.in RN，|wn(x)|≤hs(x)，andhs∈Ls(RN)，hold for any 2≤s≤2*.Dividing inequality (3.17) by ‖vn‖2，we infer that

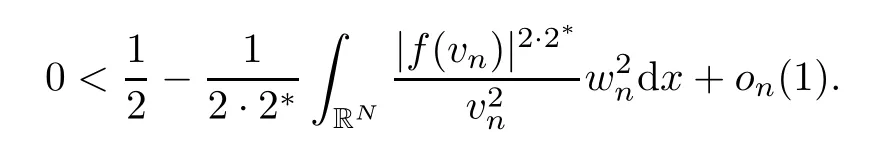
On the other hand，we observe that|[w0]|＞0 and|vn(x)|→+∞a.e.[w0]asn→∞.Under these conditions，applying Lemma 2.4(f10) and Fatou’s Lemma，we see that

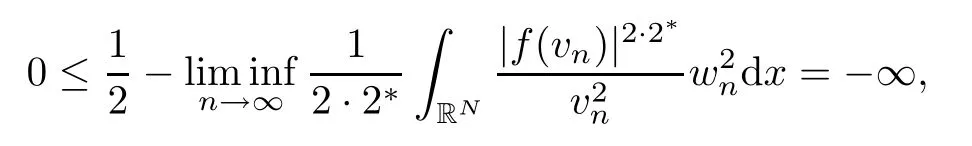
which yields a contradiction.Therefore，there existsR＞0 in such way thatJμ(v)≤0 for allv∈Qwith ‖v‖≥R.This finishes the proof. □

Corollary 3.4Suppose that (V1)，(q1)，(K1) and (h1) hold. LetQbe a finite dimensional subspace ofE.Then there existsR0＞ρ，R0depending on the dim (Q)，such that supJμ(∂QR0)≤0，whereρ＞0 is defined by Proposition 3.1 andQR0:={v∈Q|‖v‖≤R0}.

Remark 3.5Consider the subspace.Applying Proposition 3.3，there existsR0＞0 such thatJμ(v)≤0 for allv∈satisfying ‖v‖＞R0.Using Corollary 3.4，the numberR0can be taken greater thanρ.DefineandQR=Q∩BR(0) withR＞R0.Again by Proposition 3.3，Jμ(v)≤βfor allv∈Qwith ‖v‖=R，hereβcan be any positive number.Thus，β/Rγ+1→0 asR→∞for anyγ≥0.

Now，we considerμ＞μ1，whereμ1was obtained in Proposition 3.2. Define also∈=min{∈1，∈2}，where∈1and∈2were obtained in Propositions 3.1 and 3.2，respectively.Hence，we obtain the following useful result:

Proposition 3.6Suppose that (V1)，(q1)，(K1) and (h1) hold. Suppose also thatλ∈(λj，λj+1) withj≥1.Then，the energy functionalJμpossesses a (PS)cμsequence (vn)n∈N⊂E，wherecμis given by

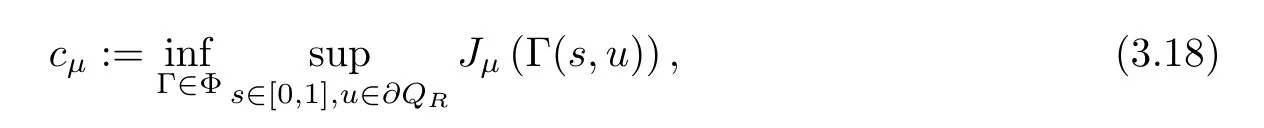
with Γ∈C([0，1]×E，E) provided thatμ＞μ1and ‖h‖2N/(N+2)≤∈.

Proposition 3.7Suppose that (V1)，(q1)，(K1) and (h1) hold. Suppose also thatλ∈(λj，λj+1) holds for somej≥1.Then any (PS)cμsequence (vn)n∈Nfor the energy functionalJμat levelcμis bounded.

ProofLet (vn)n∈Nbe a (PS)cμsequence forJμ.Given anyφ∈E，we mention that

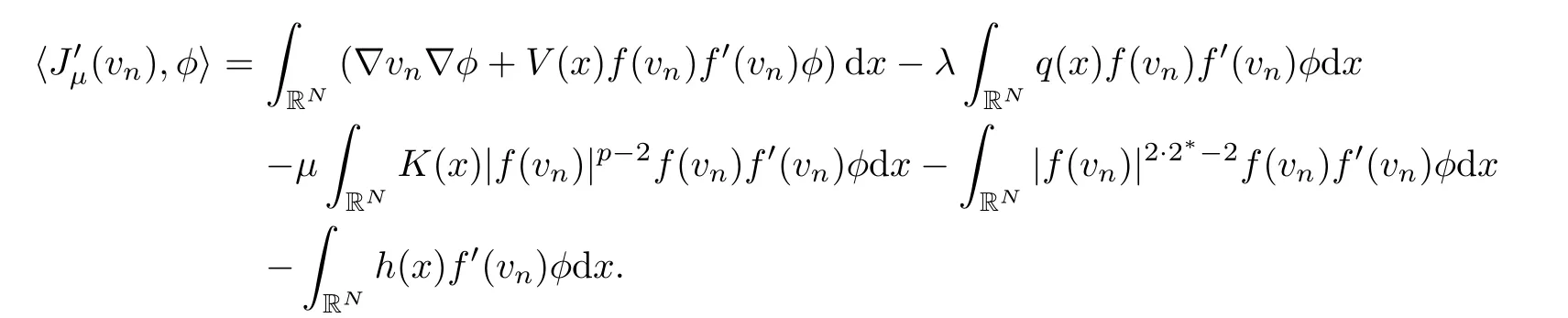
Applying Lemma 2.4，we also mention thatf(vn)/f′(vn)∈E.More precisely，we observe that

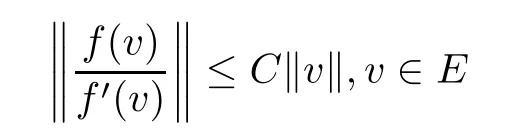
holds true for some constantC＞0.Hence，choosingφ=f(vn)/f′(vn) as a testing function，we get

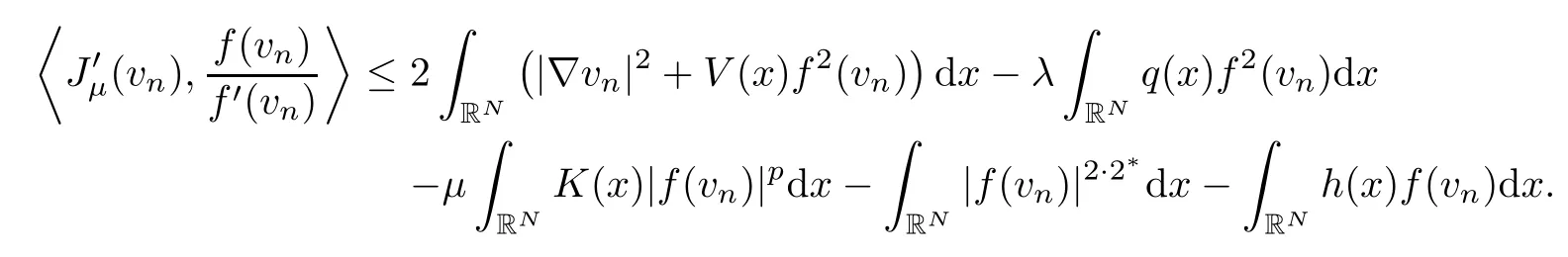
As a consequence，taking into account that (vn)n∈Nis a (PS)cμsequence，we infer that

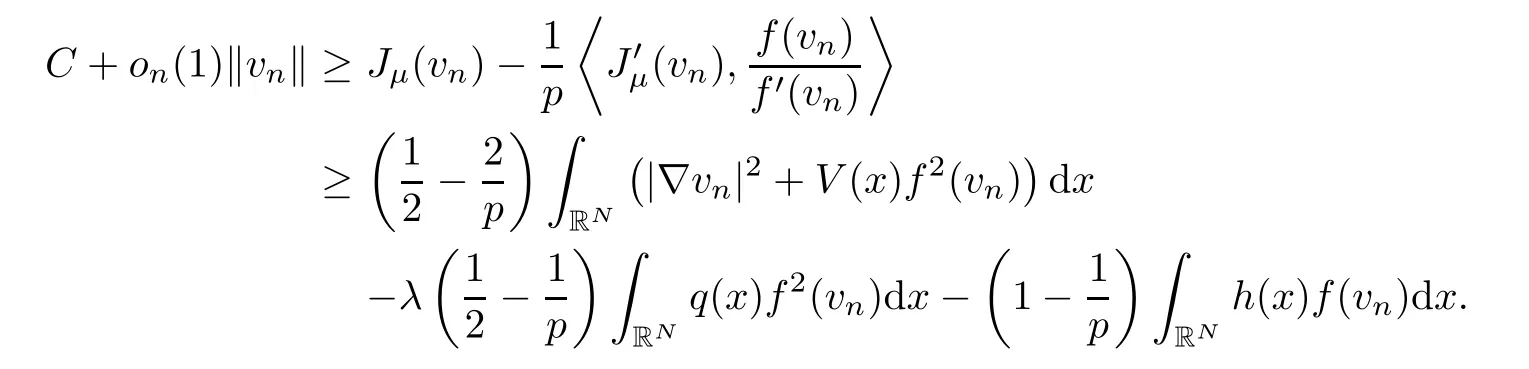
Notice that 4＜p＜2·2*.At this stage，using Lemma 2.4(f3)，(h1) and the embedding ofD1，2(RN) intoL2*(RN)，we see thatRRNh(x)f(vn) dx≤C1‖vn‖ holds true for someC1＞0

which depends only on ‖h‖2N/(N+2)and the best constant for embedding of theD1，2(RN) intoL2*(RN).Hence，we infer also that

From now on，we argue by contradiction.Suppose that，up to a subsequence，we have ‖vn‖→∞withn→∞.Define the normalized sequencewn=vn/‖vn‖ for alln∈N.Therefore，‖wn‖=1 showing the following statementswn⇀wweakly inE，wn→wstrongly in，wn(x)→w(x)，a.e.in RN，for any 1≤s＜2*.Using (3.19) and dividing by ‖vn‖2，we obtain also that

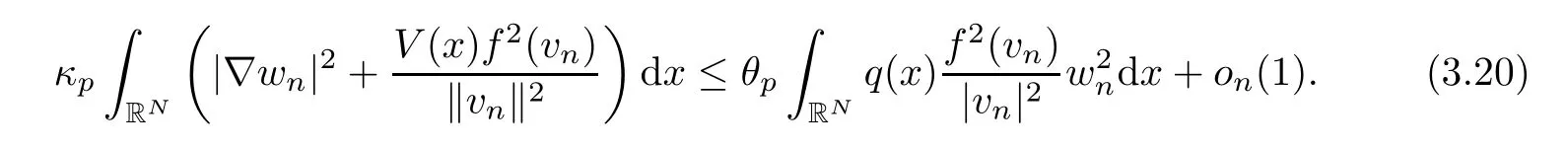
Now，we claim that

Assuming the claim given just above，it follows from (3.20) that

As a consequence，we obtain the following limits:

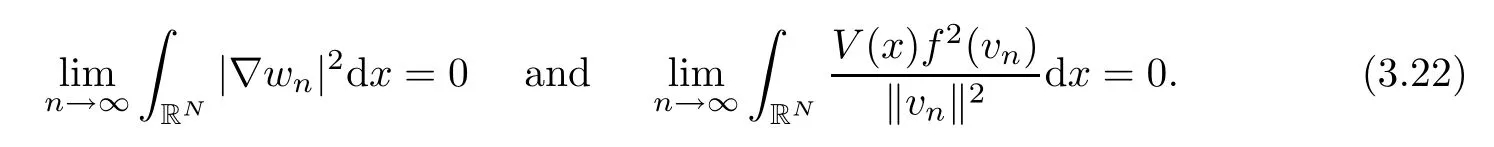
In particular，using the norm inD1，2(RN) which is weakly lower semicontinuous，we have thatw=0.However，we recall that (wn)n∈Nis a normalized sequence.Hence，applying (3.22) we get

Now，we consider the following sets:

Now，we shall prove that each integral on the right side in the identity just above goes to zero asn→∞.In order to do that for the integral overAn，we use (3.22) proving that

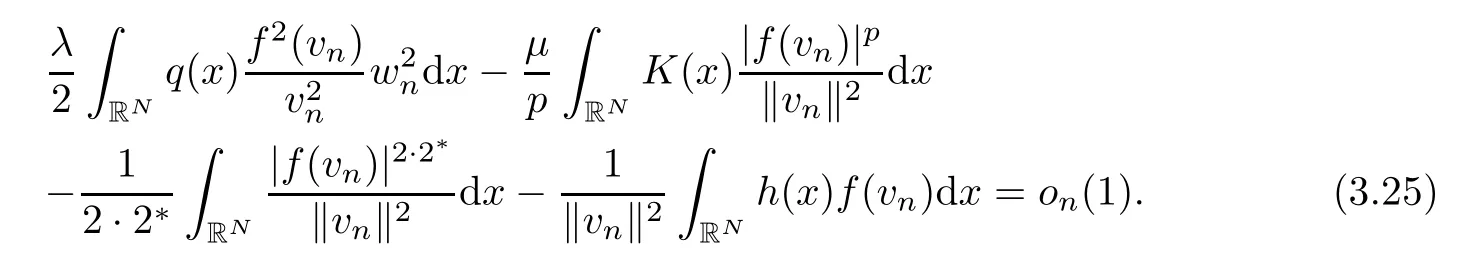
Applying Lemma 2.4(f3)，(h1)，together with the embedding ofD1，2(RN) intoL2*(RN)，we get

It follows from (3.21)，(3.26) in (3.25) that

Using (K1)，we have that

Moreover，using (V1)，we obtain that

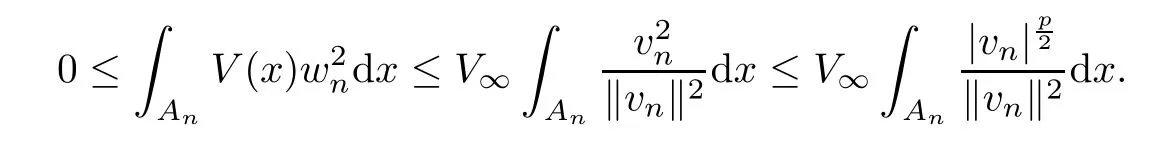
Now，applying Lemma 2.4(f8)，there exists a positive constantκ＞0 in such way thata.e.inAn.Thus，using (K1) and (3.27)，we infer that

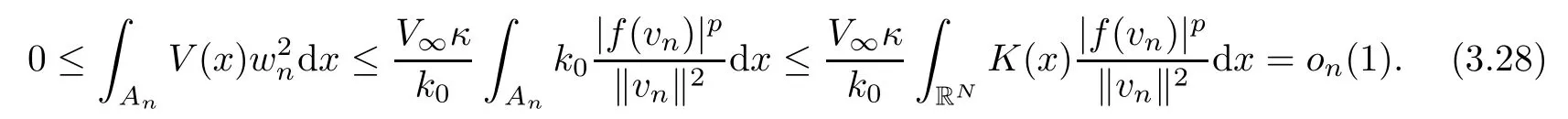
This shows that the integral overAngoes to zero asn→∞.For the integral overBn，we apply (f8) together with (3.22) showing that

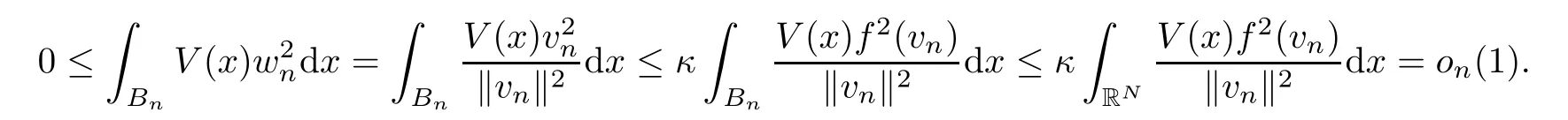
This shows that the integral overBngoes to zero asn→∞.Hence，using the last estimate above and (3.28)，we obtain that the integrals overAnandBngoes to zero.As a consequence，by using (3.24)，we also see thatRRNV(x)w2ndx=on(1).This is a contradiction with (3.23) proving that the sequence (vn)n∈Nis now bounded.

It remains to prove claim (3.21).In order to do that，we split the proof into the following two cases:

Case 1Here，we consider the casew≡0.Under this condition，we mention also that

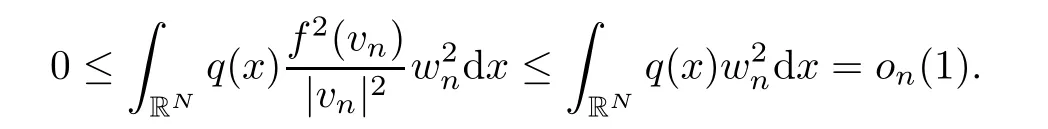
Here was used the fact that the embedding ofEinL2（RN，q）is compact.

Case 2Here we consider the case|[w0]|＞0. For this case，we observe that|vn(x)|=|wn(x)|‖vn‖→∞on[w0]. Hence，applying Lemma 2.4(f7)，we infer also thatin[w0].Using the fact that the embedding ofEinL2（RN，q）is compact one more time，we have thatwn→winL2（RN，q）.Thus，we observe thatwn(x)→w(x) a.e.in RN.Furthermore，there existsφ:RN→R withφ∈L2（RN，q）such thatAccording to Lemma 2.4(f3)，we also mention thatq(x)φ2andqφ2∈L1(RN).Thus，applying the Lebesgue Dominated Convergence Theorem，we also get.Putting all these estimates together，the proof for the desired claim follows.This ends the proof. □

For the next result，we shall employ Lions’compactness result;see[16].Similarly，as was done in[35]，the main feature is to avoid the vanish case by proving the following result:

Lemma 3.8Suppose that (V1) holds.Let (vn)n∈Nbe a bounded sequence inEsuch thatvn→0 inLs(RN) for 2＜s＜2*asn→∞.Then，we obtain the following convergences:

ProofIn order to prove the convergence described in (3.29)，we considerδ1＞0，which will be chosen later.Thus，we can write

Using the condition (V1) and Lemma 2.4(f3)，we mention that for each 2＜s＜2*，we deduce the following convergence:

asn→∞.On the other hand，by Lemma 2.4(f4)，we have that given∈＞0，there existsδ＞0 in such way that （f2(t)/t2-1）≤∈for any|t|≤δ.Thus，choosingδ1=δ，we obtain that

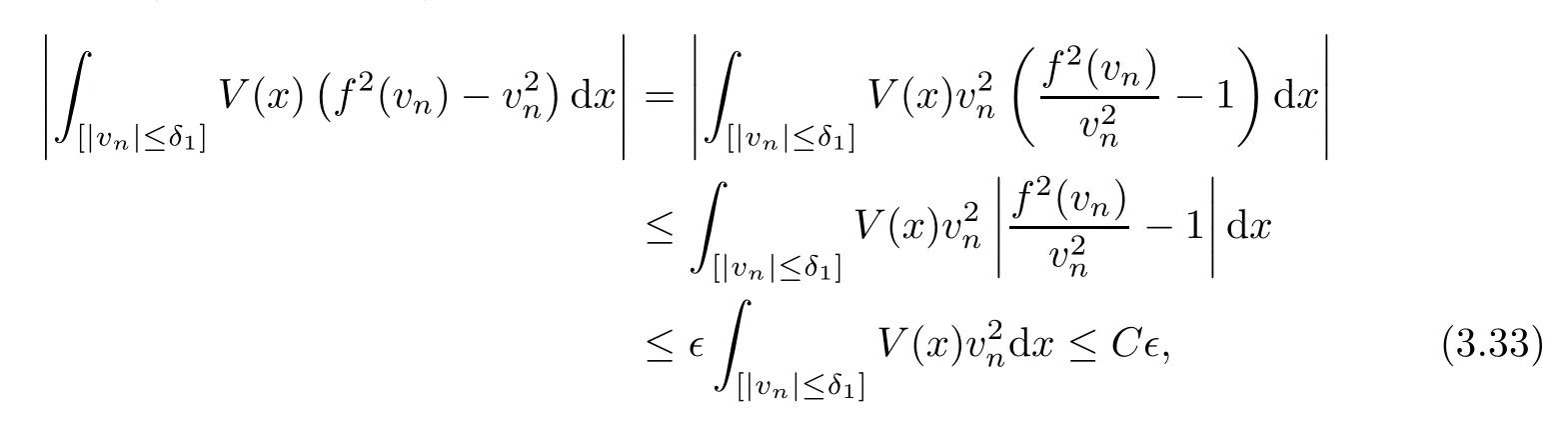
where (vn)n∈Nis bounded sequence.Therefore，using (3.32) and (3.33) in (3.31)，we obtain that

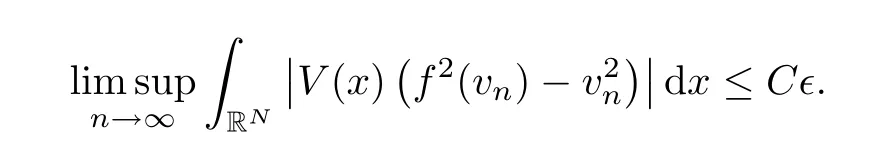
As∈＞0 is arbitrary and independent inn∈N，we obtain the convergence given in (3.29).The proof for convergence given in (3.30) follows using the same ideas discussed in the previous convergence.We omit the details. □

Lemma 3.9Let (vn)n∈Nbe a bounded sequence inEsuch thatvn→0 inLs(RN) for 2＜s＜2*asn→∞.Then，we obtain the following convergence:

ProofWe fixR＞0，which will be chosen later.Hence，we write the following identity:

By using Lemma 2.4(f7)，we get

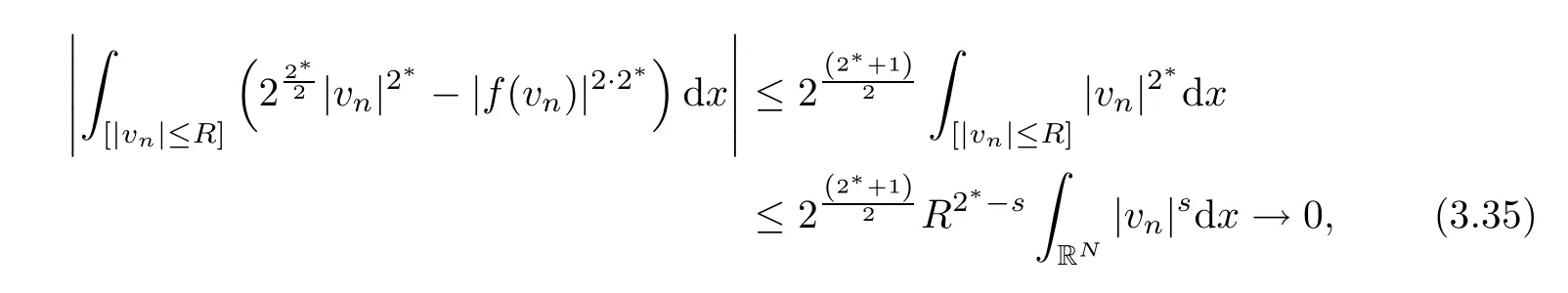
where 2＜s＜2*.On the other hand，using Lemma 2.4(f5)，given∈＞0，we can chooseRlarge enough in such way that

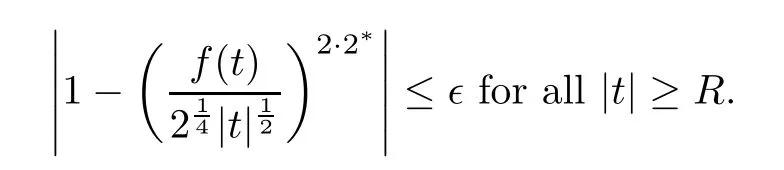
Therefore，forRlarge enough，we infer that

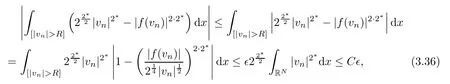
for some constantC＞0.According to (3.35)，(3.36) and (3.34)，we deduce forRlarge enough that

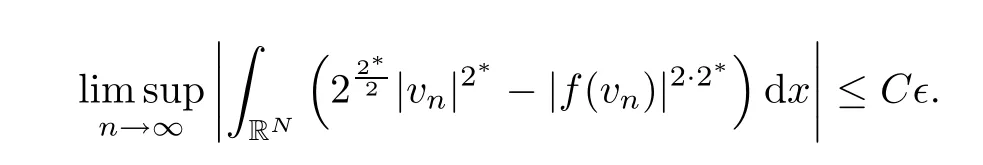
Again，as∈can be chosen arbitrarily，we conclude the proof. □

Lemma 3.10Let (vn)n∈Nbe a bounded sequence inEsuch thatvn→0 inLs(RN) for 2＜s＜2*asn→∞.Then，we obtain the following convergence:

ProofAs was done in the proof of the previous Lemma，fixR＞0 that will be chosen later.At this time，we write the following identity:

By using Lemma 2.4(f6) and (f7)，we obtain that

where 2＜s＜2*.In order to get an estimate for the integral defined in the set[|vn|＞R]，we observe that

The last assertion，together with Lemma 2.4(f5)，imply that

Thus，we can chooseRlarge enough in such way that

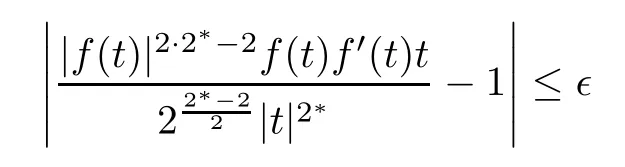
provided thatt＞R.Therefore，the last inequality imply also that

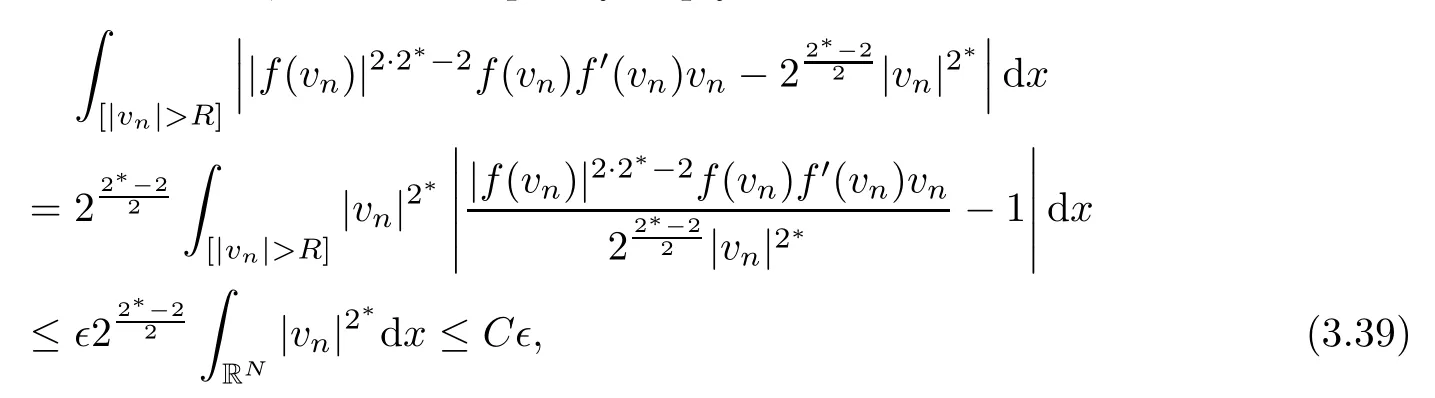
for some constantC＞0.According to (3.38)，(3.39) and (3.37) and takingRlarge enough，we obtain that

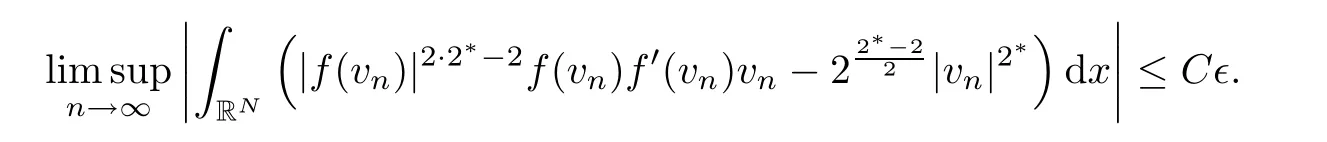
As∈can be chosen arbitrary，we conclude the proof. □

Lemma 3.11Suppose that (V1)，(q1)，(K1) and (h1) hold.Suppose also thatλ∈(λj，λj+1) for somej≥1.Let (vn)n∈Nbe a (PS)cμsequence at levelcμ＜SN/2/2Nandvn⇀0 weakly inE.Then，there exists a sequence (yn)n∈N⊂RNandr，η＞0 in such way that|yn|→∞and

ProofThe proof follows arguing by contradiction.Assume that

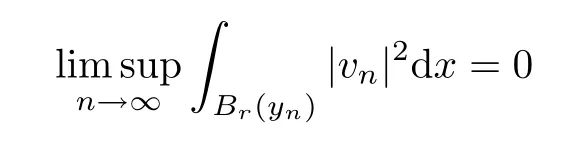
holds true for somer＞0 and (yn)n∈Nwith|yn|→+∞.Hence，we obtain thatvn→0 inLs(RN) for 2＜s＜2*;see[39].As a consequence，using Lemma 2.4(f6)，(f7)，we get

Note that (vn)n∈N⊂Eis a (PS)cμsequence for functionalJμ.Thus，we write the following identity:

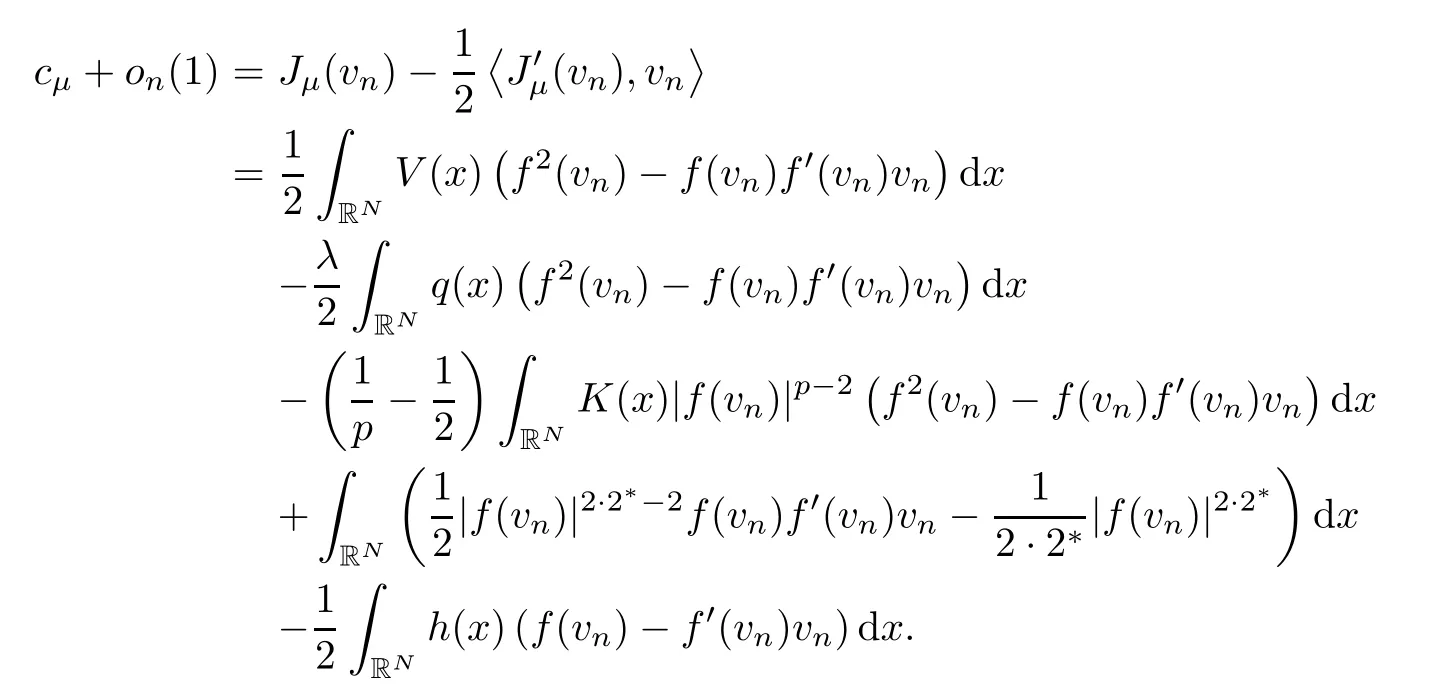
In view of (3.40) and the previous identity，we infer that

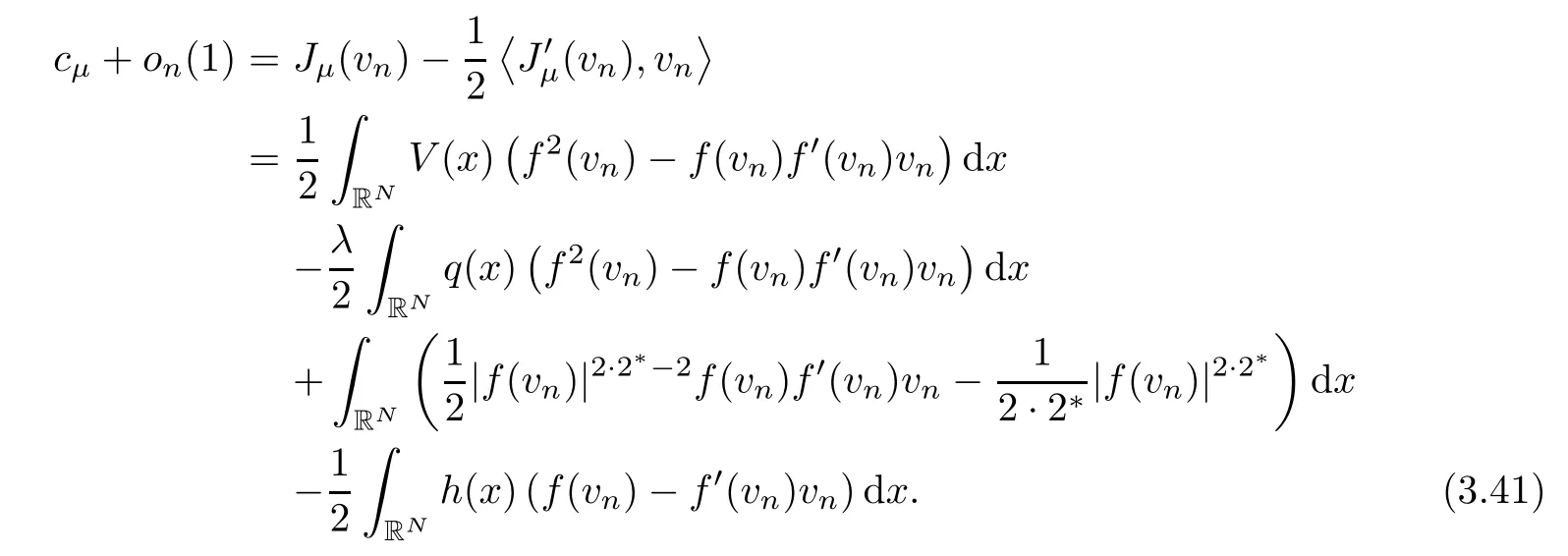
At this time，by using Lemma 3.8 we mention that

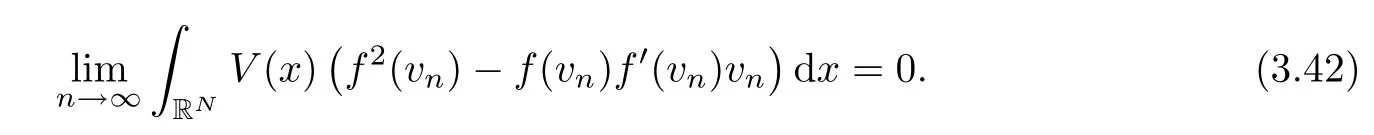
Now，applying Lemma 3.9 and Lemma 3.10，we can write

By using Lemma 2.2 and Lemma 2.4，(f3)，(f6)，we obtain that

Notice also thatvn⇀0 inEandh∈L2N/(N+2)(RN).It follows from Lemma 2.4(f2)，(f3) that

These convergences allow us to get

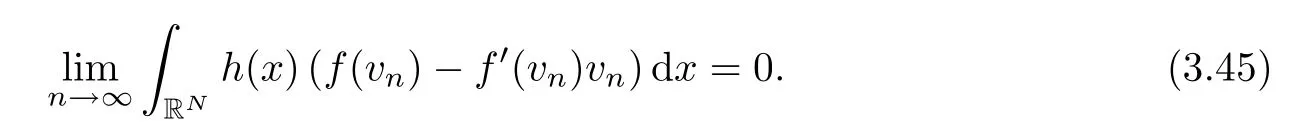
By using (3.42)，(3.43)，(3.44) and (3.45)，we write (3.41) in the following form:

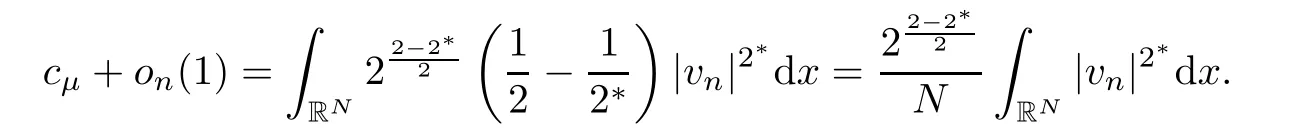
Using this last equality，we ensure also that

In view of (3.46) and Lemma 3.10，we obtain

At the same time，we claim that

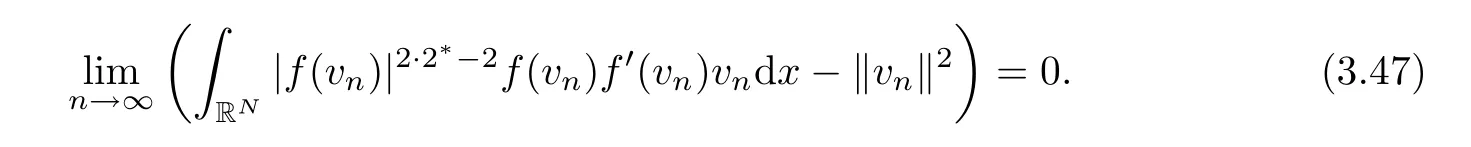
Assuming the claim just above，we infer that

Thus，using the embedding ofD1，2(RN) inL2*(RN)，we have

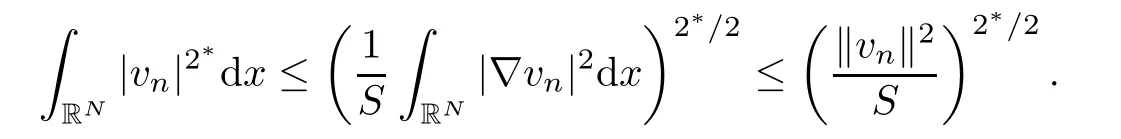
Here，Sdenotes the best constant of embedding ofD1，2(RN) inL2*(RN).In this way，taking the limit in the inequality just above and taking into account (3.46) and (3.48)，we get

Furthermore，using the fact that 2*=2N/(N-2)，we deduce thatcμ≥SN/2/2N.This is a contradiction proving that the desired result is now satisfied.

It remains to prove the claim made in (3.47).In order to do that，we observe that Lemma 3.8 provide the following identity:

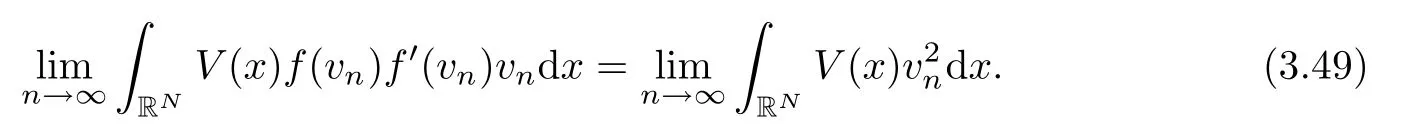
Using the condition (q1)，Lemma 2.4(f6) and Lemma 2.2，we have

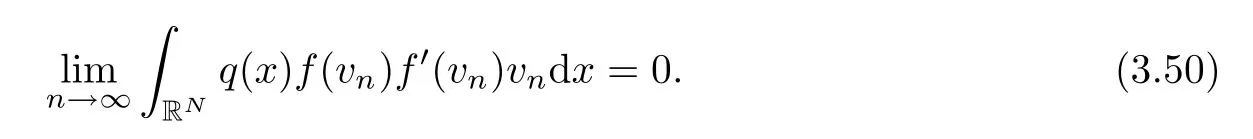
At the same time，using the condition (h1) and Lemma 2.4(f2)，we ensure also that

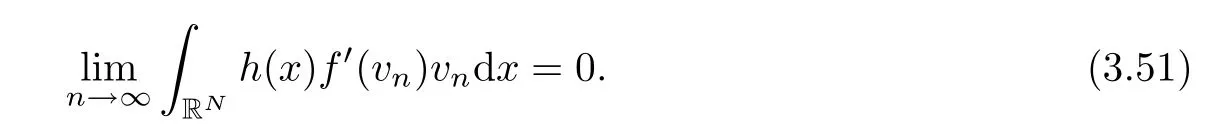
In conclusion，applying estimates (3.40)，(3.49)–(3.51) and the convergence〈J′(vn)，vn〉→0，we infer that claim (3.47) is now satisfied.This ends the proof. □

Lemma 3.12Suppose that (V1)，(q1)，(K1) and (h1) holds.Then there existsμ2＞0 in such way thatcμ＜SN/2/2Nfor allμ≥μ2，wherecμis provided by (3.18).

ProofNote that there existswμ∈Q，whereQ=E1⊕R+egiven by Remark 3.5，in such way thatIndeed，by using Corollary 3.4 and Remark 3.5，there existsR＞0 large enough satisfyingJμ(v)≤0 for allv∈QBR(0).AsJμ∈C1(E，R) andQR=Q∩BR(0) is compact，we obtain that there existswμ∈Qsuch thatAccording to Proposition 3.1，we deduce thatJμ(wμ)＞0.Thus，the last assertion says thatIt is easy to see thatfor allv∈Q.Now，we claim that ‖wμ‖→0 asμ→∞.In fact，by，and taking into account the conditions (q1) and (K1)，we obtain that

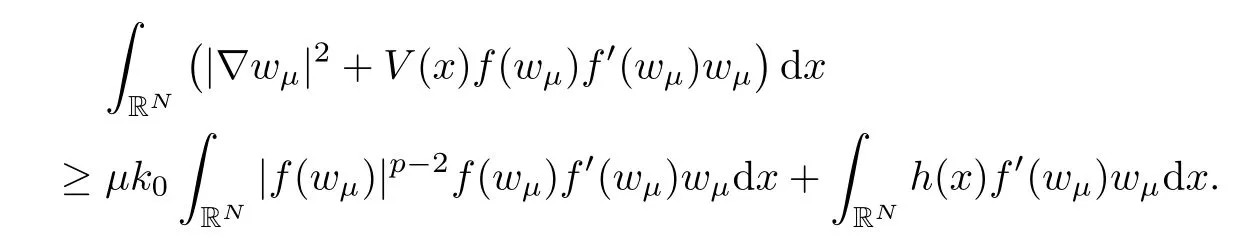
By Lemma 2.4，(f2)，(f3)，(f6)，together with (h1)，we infer that

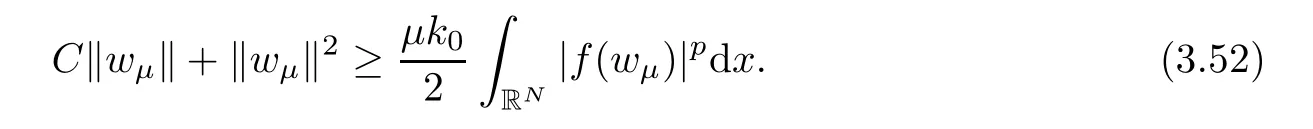
At this stage，we argue by contradiction once more assuming that ‖wμ‖/→0 asμ→∞.The proof can be done using the following cases:

Case 1 Up to a subsequence，we assume that ‖wμ‖→∞asμ→∞.

Case 2 There exist positive constantsδ，Msuch thatδ≤‖wμ‖≤Mfor allμ＞0.

Now we suppose that Case 1 occurs.Defineuμ=wμ/‖wμ‖ for allμ＞0.Then，‖uμ‖=1 for allμ＞0.Therefore，there existsu∈Qin such way that，up to a subsequence，uμ→ustrongly inQand ‖u‖=1.Hence，|wμ(x)|→∞a.e.in[u0]asμ→∞.Dividing inequality (3.52) by ‖wμ‖2，we obtain

whereoμ(1)→0 asμ→∞.Using Fatou’s Lemma and Lemma 2.4(f10)，we mention that

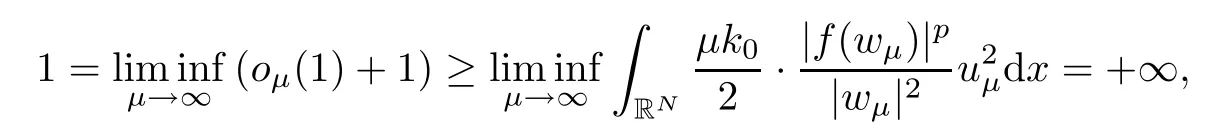
which is a contradiction proving that Case 1 is impossible.

For Case 2，it follows from inequality (3.52) that there exists a positive constantsuch thatUnder these conditions，using the fact that (wμ)μis bounded，we infer thatwμ→wstrongly inQasμ→∞.Furthermore，w0 because of the fact thatE1is finite dimensional.It follows from Fatou’s Lemma that

Therefore，‖f(w)‖p=0，which implies thatw=0 a.e.in RN.Again，we obtain a contradiction due to the fact that ‖w‖=1 showing that Case 2 is impossible.As a product，we obtain ‖wμ‖→0 asμ→∞.From now on，using the fact that ‖wμ‖→0 asμ→∞，it follows from (q1)，(K1) and Lemma 2.4(f3) that

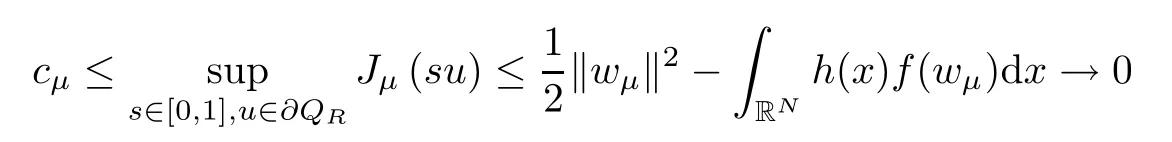
asμ→∞.Here was used the fact that the function Γ(s，u)=su.Therefore，the last assertion ensures thatcμ→0 asμ→∞.Hence，there existsμ2＞0 in such way thatcμ＜SN/2/2Nfor allμ＞μ2.This ends the proof. □

4 Proof of Theorem 1.1

In the section，we shall prove our main result given by Theorem 1.1.Initially，we chooseμ0=max{μ1，μ2}，whereμ1andμ2were given by Proposition 3.2 and Lemma 3.12，respectively.Moreover，we also choose∈=min{∈1，∈2}，where∈1，∈2＞0 are given by Propositions 3.1 and 3.2，respectively.Thus，forμ＞μ0and ‖h‖L2N/(N+2)≤∈，we invoke Proposition 3.6 to find a Palais-Smale sequence at levelcμ;that is，there exists a sequence (vn)n∈N⊂Ein such way thatwherecμis given by Proposition 3.6.According to Proposition 3.7，the (PS) sequence (vn)n∈Nis bounded.Therefore，up to a subsequence，there existsv∈Ein such way thatvn⇀vweakly inE，vn→vstrongly ina.e.in RN，and，hold true for any 1≤s＜2*.Under these conditions，we consider the following auxiliary result:

Lemma 4.1Let (vn)n∈N⊂Ebe a (PS)cμsequence at levelcμ＞0 for the functionalJμ.Then，we obtain thatvn⇀vweakly inEandJ′μ(v)=0.

ProofSince (vn)n∈N⊂Eis bounded，it follows thatvn⇀vweakly inEfor somev∈E.It remains to prove thatis dense inE，it suffices to show thatHere，the pair〈·，·〉denotes the duality betweenEandE*.Letbe a fixed function andB:=suppφ.It is not hard to see that

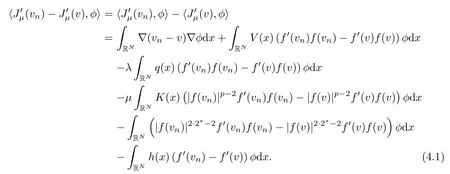
It is easy to verify thatvn→vinLs(B) for any 1≤s＜2*andvn(x)→v(x) a.e inB.As a consequence，we obtain the following convergences:

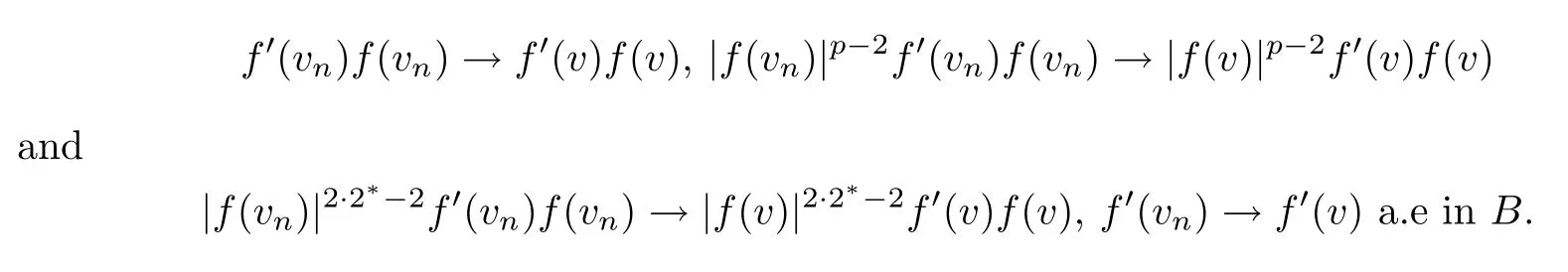
Furthermore，by using (V1) and Lemma 2.4(f9)，there exists a positive constantCwhich does not depend onnsatisfying the estimate|V(x)f(vn)f′(vn)φ|≤C|φ|.Thus，the sequenceV(x)f(vn)f′(vn)φis dominated by function inL1(B). Again，using Lemma 2.4(f9)，we get|q(x)f(vn)f′(vn)φ|≤2-1/2|q(x)φ|.It follows from (q1) and Hlder’s inequality thatqφ∈L1(B).Therefore，q(x)f(vn)f′(vn)φis dominated by function inL1(B).Moreover，using (K1) and Lemma 2.4(f7)，(f9)，we also see that

Now，choosings=p/(p-2)，Hlder’s inequality shows that|hs|(p-2)/2φ∈L1(B).Thus，K(x)|f(vn)|p-2f(vn)f′(vn)φis dominated by function inL1(B).Analogously，we observe that|f(vn)|2·2*-2f′(vn)f(vn)φis dominated by function inL1(B).Moreover，using Lemma 2.4(f2)，the last estimates implies that

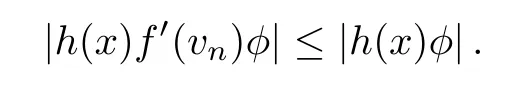
Moreover，using (h1) and Hlder’s inequality，we also mention thath(x)φ∈L1(B).It follows thath(x)f′(vn)φis dominated by function inL1(B).Putting all these estimates together in (4.1)，we obtain from the Lebesgue Dominated Convergence Theorem that

It is important to emphasize that Lemma 4.1 ensures that our main problem (1.2) admits at least one solution for anyh∈L2N/(N+2)(RN).For eachh0，the proof of Theorem 1.1 is now done.Furthermore，forh≡0，we need to guarantee that our weak solutionvfor problem (1.2) is not trivial.Therefore，we shall treat the case whereh≡0 is satisfied.Notice that，assuming thatv0，the proof for Theorem 1.1 follows using Lemma 4.1;that is，assuming thatv0，we obtain a nontrivial critical point for the energy functionalJμ.It remains to consider the casev≡0 andh≡0.In this setting，we need to ensure that our main problem (1.2) admits at least one nontrivial weak solution.In order to do that，as a first step，we recall that

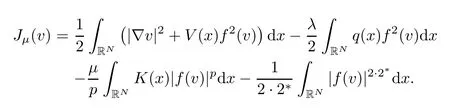
It is worthwhile to mention that the energy functional given just above satisfies the linking conditions provided by Theorem 2.1.For our purpose，we assume thatvn⇀0 inE.In view of Lemma 3.11，there exists a sequence (yn)n∈Nandr，η＞0 in such way that|yn|→∞ and

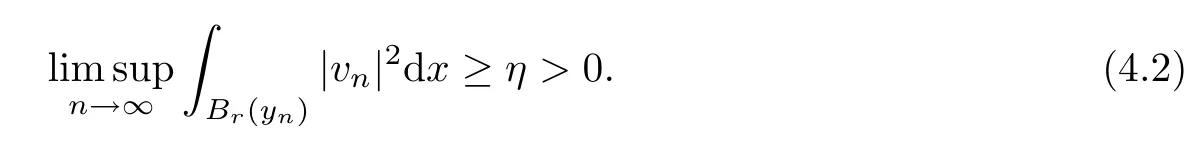
Define the shift sequenceun(x)=vn(x+yn)，x∈RN.Without any loss of generality，we assume that (yn)n∈N⊂ZN.Now，we mention that (un)n∈Nis also bounded.In fact，using hypothesis (V1) and the translation invariance in RN，we know that ‖un‖=‖vn‖.As a consequence，we deduce that (un)n∈Nis also bounded.Thus，un⇀uinEfor someu∈E.Hence，using (4.2)，we infer thatu0.

In what follows，we prove that the weak limit for the shift sequence is a critical point for the functionalJμ;that is，we have thatholds true for anyφ∈E.In order to do that，fixing，we observe also that

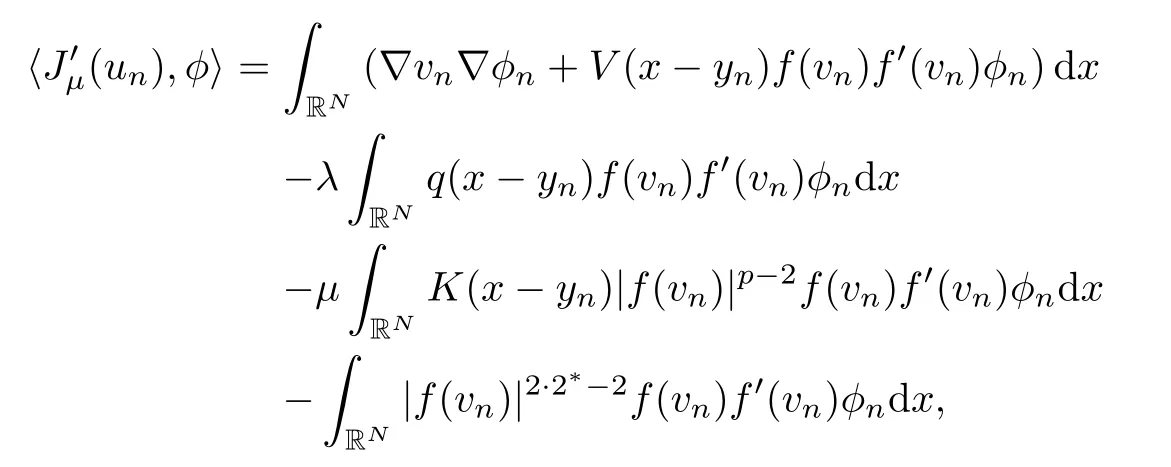
whereφn(x)=φ(x-yn) for alln∈N.Using the conditions (V1) and (K1) in the above equality，we have that

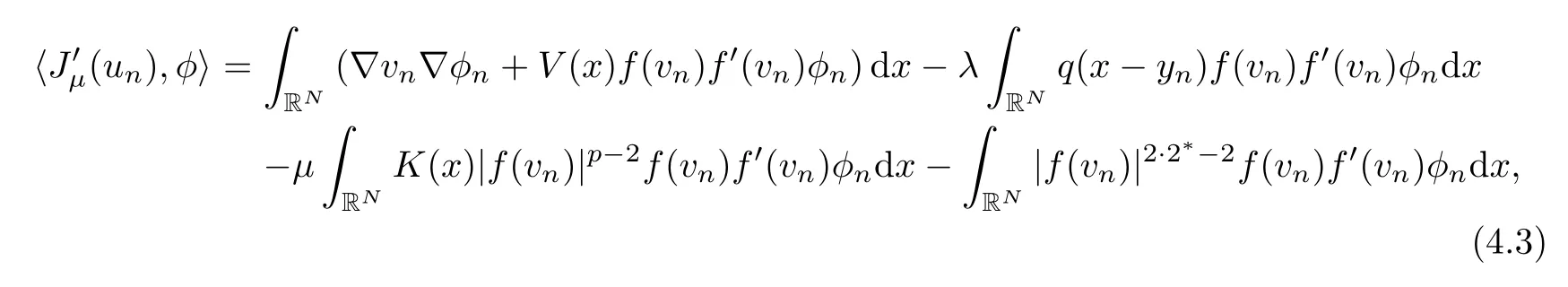
Since (vn)n∈Nis a (PS)cμsequence for the functionalJμ，we infer thatasn→∞.Using the last convergence and (4.3)，we deduce that

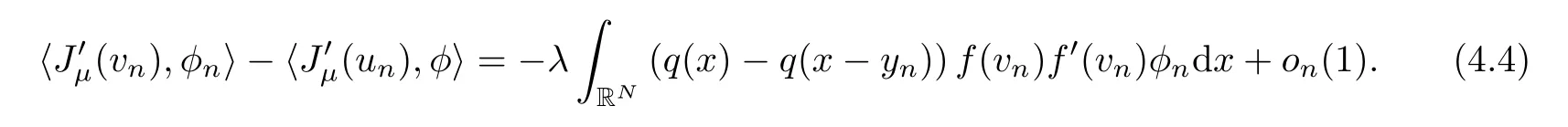
Here was used (V1) and (K1) together with the fact that the functionsVandKare 1-periodic for eachxiwith 1≤i≤N.Now，we claim that

Indeed，for anyR＞0 we observe that

The idea is to ensure that the integrals in right side in (4.6) goes to zero asn→∞.Using Lemma 2.4(f2) and (f3)，Hlder’s inequality implies that

where 1/α+2/r=1 andAφ=RBR|[q(x)-q(x-yn)]f(vn)f′(vn)φn|dx.Asα＞N/2，we see also thatr∈(2，2*).Hence，the last estimate，together with the Sobolev compact embedding，say thatRBR|[q(x)-q(x-yn)]f(vn)f′(vn)φn|dx→0 asn→∞.On the other hand，using Hlder’s inequality one more time，we deduce the following estimates:

whereC＞0 andBφ=RRNBR|[q(x)-q(x-yn)]f(vn)f′(vn)φn|dx.Furthermore，we mention that

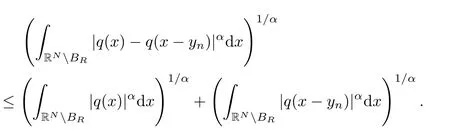
Asq∈Lα(RN)，there existsR∈＞0 such thatfor anyR≥R∈and for any∈＞0.At this stage，for alln∈N，using (q1) and Remark 1.3，we also mention thatfor anyR≥R∈and for each∈＞0.Under these conditions，as∈＞0 is arbitrary，the claim given in (4.5) is now verified.Thus，applying (4.4) and (4.5)，we obtain thatUsing the fact thatwe getTherefore，arguing in a similar way as was made in the proof of Lemma 4.1，we infer thatuis a nontrivial critical point of the functionalJμ.This ends the proof of Theorem 1.1.