中风化砂砾岩地层泥水平衡长距离顶管总顶力的计算

蒋尊正，杨泽矗

（巢湖市重点工程建设管理中心，安徽 巢湖 238000）

顶管施工成败的关键是正确选择顶力计算，但其理论方面的研究相对滞后于施工工艺的进展，这在一定程度上限制了顶管技术的进一步发展。对顶管工艺中最基本、最重要的参数—顶力的计算,不同类型的公式的适应情况不同，各种顶力方法都有其局限性。在特定地质情况下，选用相适应的计算方法与参数，对顶力各主要影响因素进行细致的理论分析，结合实际施工条件建立合理的顶力计算模型，推导出计算结果可靠的理论顶力而进行研究，为实际工程应用提供参考，既可以为顶管工程的关键内容做出初步合理的设计，又对施工现场具有一定的指导作用。因此，对中风化砂砾岩地层泥水平衡长距离顶管总顶力进行细致的理论分析具有重要的意义。

1 影响顶力的主要因素

式中：τ1为泥浆与管节接触部分的剪应力；τ2为土体与管节接触部分的剪应力；S1为管节与泥浆的接触面积；S2为管节与土体的接触面积[2]。

2 土压力计算理论的选择

土压力计算理论的选择计算是顶力计算的重要内容,不同的土压力计算理论的选择对顶力计算会产生很大的影响。常见的土压力计算理论包括土柱法、普氏卸荷拱法、太沙基法及马斯顿法。不同的土压力计算理论的选择对顶力计算会产生很大的影响。因此有必要结合顶管施工特点引入合适的土压力计算理论，对顶力计算理论进行分析。四种土压力理论中，土柱理论未考虑土体存在卸荷压力拱，仅考虑覆土厚度和土的重度，其计算值最大。普氏理论和太沙基理论计算值相近，但普氏理论未考虑浅埋深埋的区别，具有一定局限性。马斯顿理论计算值最小，这是因为马斯顿理论多考虑了土的粘聚力的影响。总结来说，太沙基理论和马斯顿理论的适用性更强。马斯顿理论考虑的更全面，计算较为合理，所以在覆土深度满足情况下，优先选择马斯顿理论进行计算[3]。

3 顶力的组成

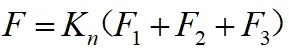
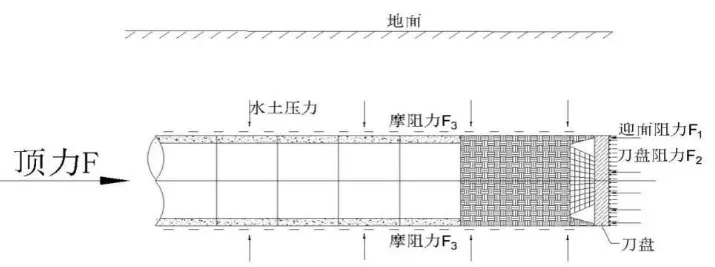
图1 顶管顶力计算示意图

式中：F—顶管总顶力（kN）；F1—迎面阻力（kN）；F2—刀盘阻力（kN）；F3—摩阻力（kN）；Kn为考虑瞬时性的安全系数，一般取值1.05～1.1。

3.1 机头迎面压力所需的推力F1

机头迎面阻力F1与掌子面的水平土压力PH、顶管外径R和水压力Pw有关，迎面阻力是由作用于正面的水±压力而产生的阻力，以中心线处的阻力作为平均阻力计算顶进前端总的正面阻力且在计算过程中应考虑地下水的影响[4]，水平土压力为作用在顶管管节两侧及顶管机前端，沿其横断面水平方向作用的分布荷载。其大小根据垂直土压力与侧向土压力系数来计算的。泥水平衡顶管，为了在开挖面形成泥浆套，必须使泥水压力高于地下水压力，以便泥水向土体渗透，并填堵土体中的孔隙。因此。在决定泥水压时，一般还需在水土压力的基础上再加一部分预留压力。通常预留压力▽P取值为10--30kPa[5]。

泥土(水)压=水平土压+地下水压+预留压力。

式中：Kh——侧向土压力系数，

式中：rw—水的容重；hw—地下水位距刀盘中心的高度(m)；Φ—土的内摩擦角；q根据土层渗透系数确定的经验数值。

对于砂土q=0.5～1.0；粘性土q=0.1～0.5；风化岩层q=0～0.5。对粘土层而言，通常是把地下水压力计在土压力中。地下水压力的大小与水力梯度、地层渗透系数、渗透时间有关。由于地下水流经土体时受到土体的阻力产生水头损失，因此作用在刀盘上的水压力一般小于该地层处的理论水头压力。

3.2 刀盘阻力F2

在砂砾石地层中，当刀盘上的刀具切削锥体时，顶管刀盘的滚刀必定会贯入地层必须要克服一定的地层阻力。对于克服刀盘承受的开挖面阻力所需的推力F2国内外学者已展开了大量的研究,美国科罗拉多大学矿业学院通过线性切割实验研究所得出的滚刀受力公式，相对其他学者所得出的公式更符合实际情况，准确性更高，故选取CSM公式作为顶管顶进时的正面推进阻力刀盘阻力理论值计算公式[6]。

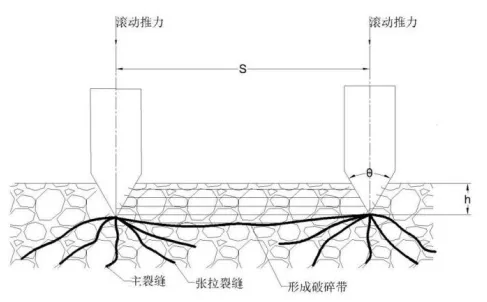
图2 滚刀破岩示意图

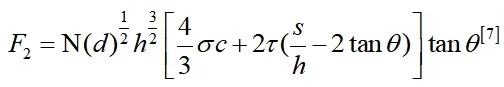
式中：N—滚刀数量，d—盘形滚刀直径，h—盘形滚刀切入岩石深度，S—刀间距，θ—盘形滚刀刃角，σc—岩石单轴抗压强度，τ—抗剪强度，MPa；

3.3 管道与周围地层摩擦阻力F3

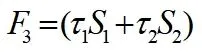
式中：τ1为泥浆的剪应力；S1为与泥浆的接触面积；τ2为管土之间剪应力；S2为与周围土体的接触面积。

式中：K为流体稠度系数,n为流型参数。n与K均可采用范式六速旋转黏度计测触变泥浆得到。

式中：l1为管节与泥浆的宽度，l2为管节与土体接宽度，Pu为管段土体每延米相互作用力，E’为土体的弹性模量，基于统计损伤理论的方法进行分析，滚刀产生的裂隙将对岩石弹性模量产生影响，基于类似岩石的研究成果，当Pw=3MPa时，E’≈1/2.3E[9]E为岩石未产生裂隙前弹性模量，ν为土体的泊松比，E0为混凝土管的弹性模量，ν0为混凝土管段的泊松比。

可计算出土体与管段接触宽度l2

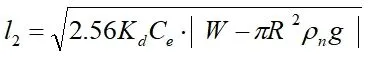
法向应力：

φ为管土接触位置与管节中心线的夹角。

图3 管道在注浆条件下与土体接触模型

由于顶进初期泥浆套成型效果不好，泥浆减阻未能充分发挥、轴线控制不太稳定等施工因素造成的。随着顶进长度的增加，泥浆套及轴线控制慢慢呈现稳定状态，单位长度摩阻力随着顶程的增加而减少。在类似施工条件下：

稳定阶段触变泥浆性能随着时间而变化；泥浆套形态也随着触变泥浆在土体中的渗透作用及水分从触变泥浆中离析而产生形态变化；随着顶进距离的延长，轴线偏差致使管道外侧土压力不对称的叠加对轴向顶力多重分解作用，后续管节传递的顶进力侧向分力增大，造成顶管侧摩阻力也随之增大。表现在稳定阶段单位长度摩阻力随着顶程的增加，呈线性增加。在类似施工条件下：

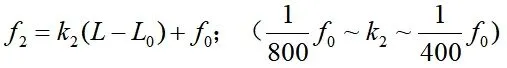
单位摩阻力理论上存在一个最小值，管节在空腔里顶进，受外力出现垂直管节前进方向位移，由均布荷载挠度计算公式，当位移量等于2倍管节间隙时，管节重新处于稳定状态，此时管节形成稳定泥浆套，轴向偏差积累的次数较小，以此顶进长度作为划分相应“初始阶段-稳定阶段”的分界点。则：

4 工程案例计算分析

以巢湖市巢湖大桥电力隧道工程为例，通过现场实测中风化砂砾岩地层条件下采用泥水平衡顶管顶进过程中顶进力的变化情况，系统研究影响顶进力的因素及其变化规律，并对顶进力的计算进行了理论分析，与实际顶进力进行了对比，得出在该地质条件下的泥水平衡顶管顶力计算公式。计算参数取值如表2所示。

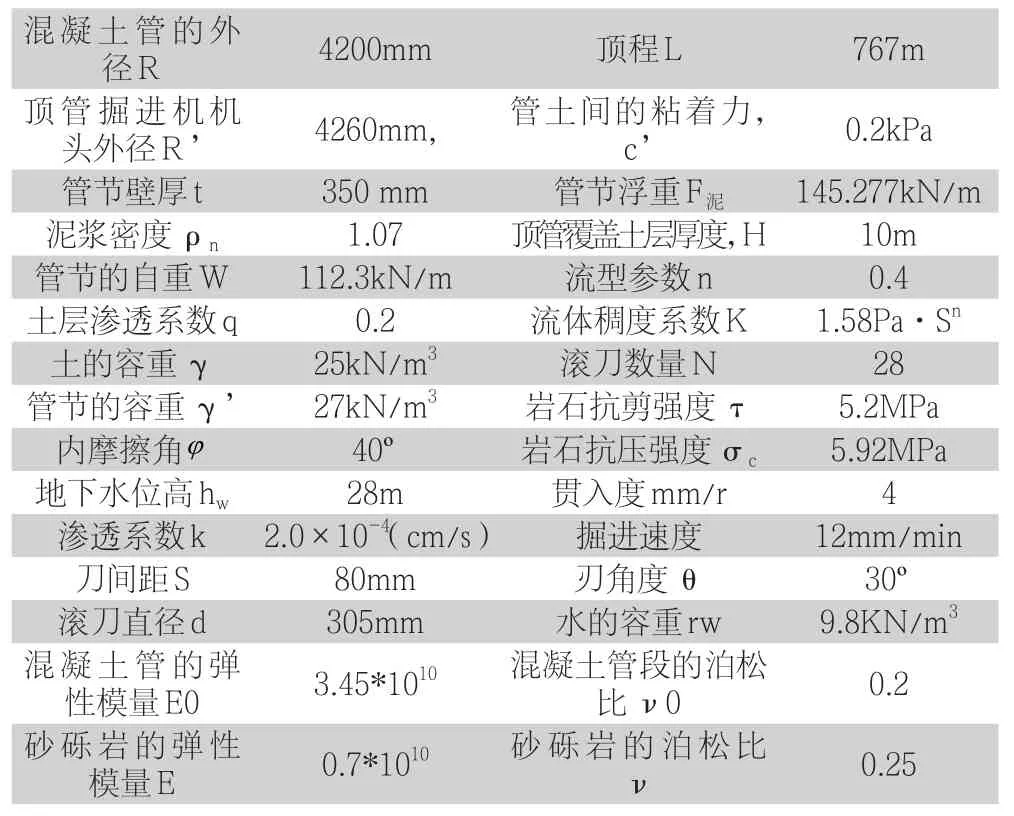
表2 计算参数

4.1 土压力计算

因为管节不可能收拉，故管节上方所受压应力为零。则作用于单位长度管道上的管周总法向土压力为零。

4.2 管周摩擦阻力的推导

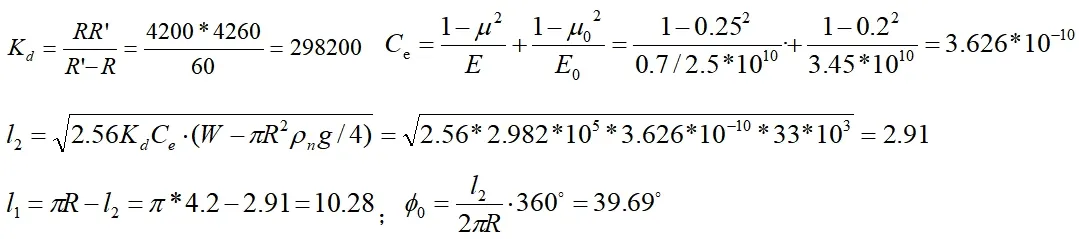
将接触角φ0代入法向接触应力公式进行积分得：接触合力P=1.06Pu。

4.3 顶力的组成计算

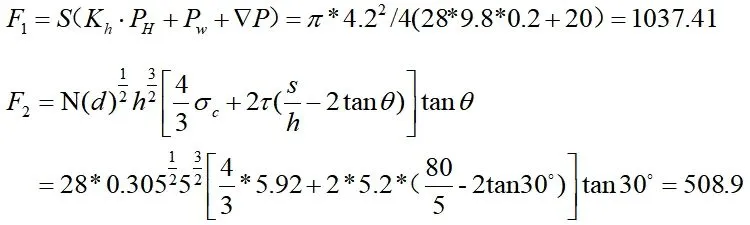
在现场数据收集的基础上，把实测L=L0处及L=5L0处顶力数据代入公式：

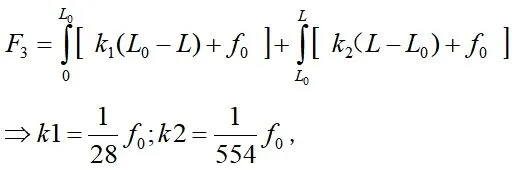
将结合现场部分数据得出的k1、k2值代入F3，算出各段顶力随顶距的变化关系，作出F与顶距L的关系曲线，

4.4 理论顶力与现场实测顶力及新公式计算结果的对比分析

以上计算过程中，由于计算参数的选取灵活性，计算结果可能略有出人。从公式中可以看出，顶管顶力与许多因素有关，各公式选取一部分因素纳人计算。从上图中可以看出，本公式的计算结果与现场实测顶力拟合性很好。现有公式在顶力计算中偏于保守；随着顶进距离的增加现有计算公式顶力呈线性增加，而实测顶进力呈曲线上升趋势，表明长距离顶管施工过程中摩阻力的变化规律有待分析考虑，以反映真实各影响因素。

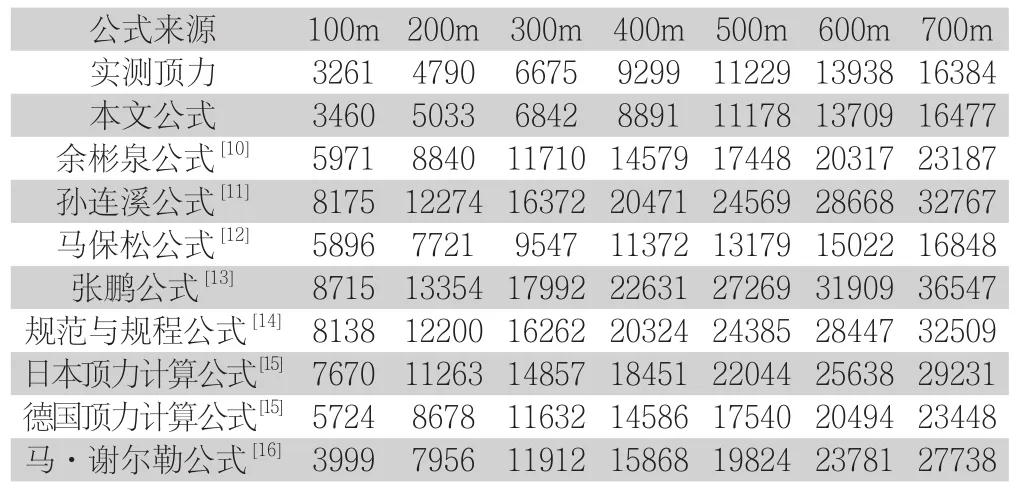
表3 顶管顶力对比KN

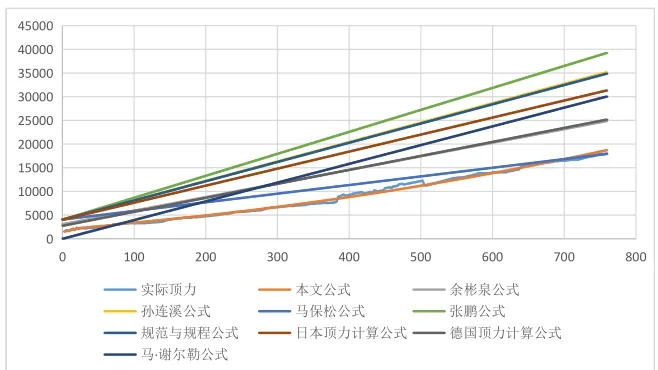
图4 管道顶进项力计算及实测顶力

5 结论

通过理论分析，结合现场实测数据，本文公式对顶力变化趋势较好反应，在中风化砂砾岩地质条件下，对采用泥水平衡顶管掘进的顶力进行了理论分析计算，并通过分析实测顶力和单位摩阻力,综合以上分析得出顶力的表达公式，可作为今后同类工程顶力计算的理论基础。本文提出的顶力计算方法适用条件明确，计算结果可靠，与现有公式计算结果相比更接近实测值，尤其是在实际顶管过程中需要考虑卸荷拱效应的情况下。顶管顶进力与工程地质条件和施工状态等因素有直接关系且影响较大，在设计和施工中应在合理预估总顶力的前提下保证工程的安全性和经济性。