地震作用下不同截面车站结构动力特性研究
任青阳,彭子健,王飞飞,赵梦园
(1. 山区桥梁及隧道工程国家重点实验室 重庆交通大学,重庆 400074; 2. 重庆交通大学 土木工程学院,重庆 400074)
0 引 言
1995年发生的阪神地震中,大开、长田等许多地铁车站发生了不同程度的震害[1-2],尤其是大开地铁车站的破坏程度最为严重,诸多中柱发生严重变形破坏,顶板被折断而呈“M”型,路面发生塌陷。而据该地铁车站的设计资料表明,设计中取用的安全系数较高,设计中柱的安全系数高达3,但由于设计时没有充分考虑地震作用的影响,所以对于抗震能力的设计存在很大程度上的不足。
对于最终导致车站结构塌毁的外因,学者们普遍解释为由地震产生的土层水平变形作用在地下结构上的剪切作用为主因[3-4],同时也有一些研究人员认为竖向地震作用是致灾的主因[5],还有专家认为是水平地震作用和竖向地震作用的共同作用导致了地下结构的塌毁[2]。而对于大开地铁车站地震塌毁的内因,多数的认识是由于中柱结构的抗震性能不足导致的[2],部分研究者也对侧墙或其他主体结构的强度情况进行了研究[4]。结合上述分析,有学者提出水平地震作用导致的土层水平变形作用在地下结构上的剪切作用是主要原因,但受到竖向地震作用的影响,中柱结构的抗剪性能与抵抗变形的能力变差,最终导致了破坏[6]。其中有学者提出是由于竖向地震作用使结构上覆土体整体性遭到破坏,形成独立的土块,并在竖向地震作用下产生惯性力效应,进而增大了中柱承受的轴压比,导致中柱的抗剪性能与抵抗变形的能力变差,最终破坏[7-10]。由上述研究成果可知,车站结构的破坏始于关键构件中柱的破坏,高轴压比下,中柱的脆性增加,抵抗变形的能力变差,在水平地震荷载的作用下无法承受顶板传递的强制水平位移而发生脆性破坏。随着中柱发生大变形退出受力,顶板延横向的跨长大幅增加而产生较大弯矩,从而被折断引起整体结构的破坏。
为缓解地震作用下中柱的高轴压比工作环境,提高中柱抵抗水平变形的能力,拟对车站结构截面形态进行改变。笔者参考大开地铁车站的截面尺寸,在其基础上将顶板形态改为拱形,并通过改变弧线对应圆心角的大小来控制截面形状,从而探究了不同截面形状下车站结构的位移响应以及竖向荷载分布情况。通过ABAQUS进行了数值建模,首先通过建立二维整体有限元模型获得了不同截面形状下的中柱端部相对位移响应以及车站结构所承受的竖向荷载在中柱以及侧墙上的分布情况;建立了三维中柱精细化模型,通过将二维分析中获得的中柱端部相对位移响应作为荷载施加在三维中柱精细化模型顶面上,实现中柱的钢筋与混凝土分离建模,进行了更加真实的弹塑性时程分析仿真[11],从而验证了通过改变车站截面形状改善车站关键构建受力环境的可行性以及有效性。
1 二维车站整体有限元模拟
1.1 模型与边界
二维模型的建立是为了更加高效地获取中柱两端在水平地震作用和竖直地震作用耦合作用下的相对水平位移及相对竖直位移时程曲线,因此需对地铁车站进行整体模拟。
参考日本大开车站的断面形式建立分析模型。如图1,为一单层双跨车站,车站顶板埋深4.8 m,结构断面高7 m,宽18 m,顶、底板厚度依次为0.8、0.9 m,侧墙厚0.8 m。中柱断面尺寸为400 mm×1 000 mm,矩形截面车站对应柱高为3.62 m,拱形截面车站对应柱高为4.79 m。
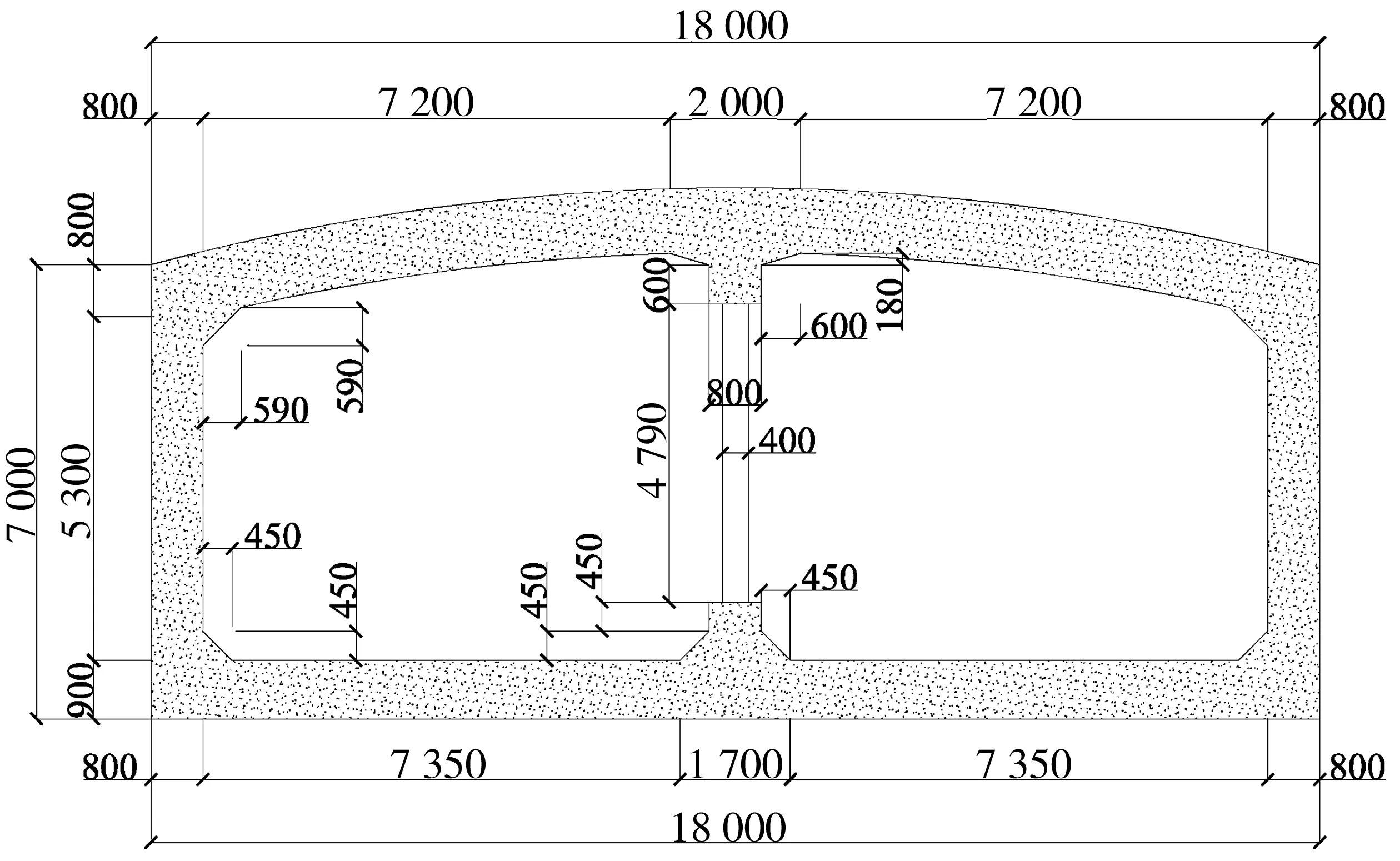
图1 地铁车站主体结构(单位:mm)Fig. 1 Main structure of subway station
如图2,模型底面取在地下24 m处,模型计算宽度取车站宽度的4倍,即72 m,模型左右两侧及底部均采用黏弹性人工边界。采用平面应变缩减积分单元(CPE4R)对模型进行离散。
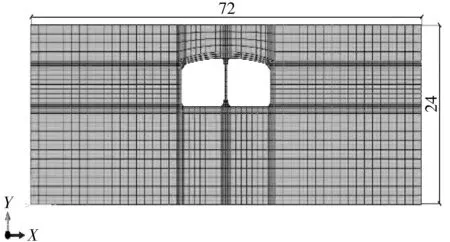
图2 二维有限元模型(单位:mm)Fig. 2 2D FEM model
1.2 材料参数及本构模型
采用Mohr-Coulomb模型来描述土的变形特征,该模型能够描述土体变形的基本特征,简单实用,参数少。出于简化考虑,笔者对土体进行了均一化处理。根据文献[12]提供的该场地的地层情况及物理参数等效而得,取土体密度为1.96 g/cm3,杨氏模量为180 MPa,泊松比为0.3,内摩擦角取为33°,黏聚力为30 kPa,剪切波速Cp=351.6 m/s,Cs=187.9 m/s。
中柱将钢筋弥散进混凝土的方式进行模型的建立,采用混凝土塑性损伤模型,密度为2.5 g/cm3,杨氏模量为42.6 GPa,泊松比为0.2。车站其他主体结构同样采用混凝土塑性损伤模型,密度为1.96 g/cm3,杨氏模量为40.2 GPa,泊松比为0.2。模型需提供混凝土单轴应力-应变关系及加载卸载应力路径。由于结构受拉时,力的主要承担者是钢筋,而混凝土可以通过与钢筋的黏结滑移作用将力传递给钢筋,所以笔者在此模型基础上采用修改后的拉伸行为。如图3,以混凝土开裂与否作为界限,开裂前取规范规定的混凝土单轴拉伸曲线,开裂后以线性减少到计算终值。单轴压缩行为曲线与单轴拉伸行为曲线一样,参照GB50010—2010《混凝土结构设计规范》进行取用。
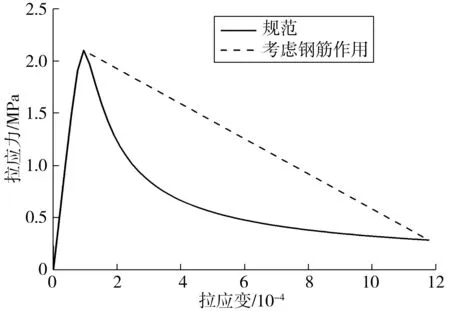
图3 混凝土单轴拉伸应力-应变曲线Fig. 3 Uniaxial tension stress-strain curve of concrete
此外,在混凝土塑性损伤模型中还有一个需设参数为塑性损伤因子,在GB50010—2010《混凝土结构设计规范》中也有明确的定义以及计算公式,由于开裂后混凝土结构中的拉伸应力主要由钢筋承担,混凝土单轴拉伸行为曲线取为线性,所以无需定义拉伸行为的损伤因子。记压缩损伤因子为dc,其定义为:
(1)
式中:E0为初始弹性模量;Ec为压缩状态下卸载路径的弹性模量。
以C30混凝土为例进行模型验证。图4为数值模拟下单轴压缩荷载作用下的应力-应变关系与理论曲线的对比,从图4中可以看出,由ABAQUS模拟的应力-应变曲线与GB50010—2010《混凝土结构设计规范》给出的单调应力-应变曲线基本吻合,笔者所采用的混凝土塑性损伤本构模型用于研究地震作用下混凝土结构的响应特性是可行的。
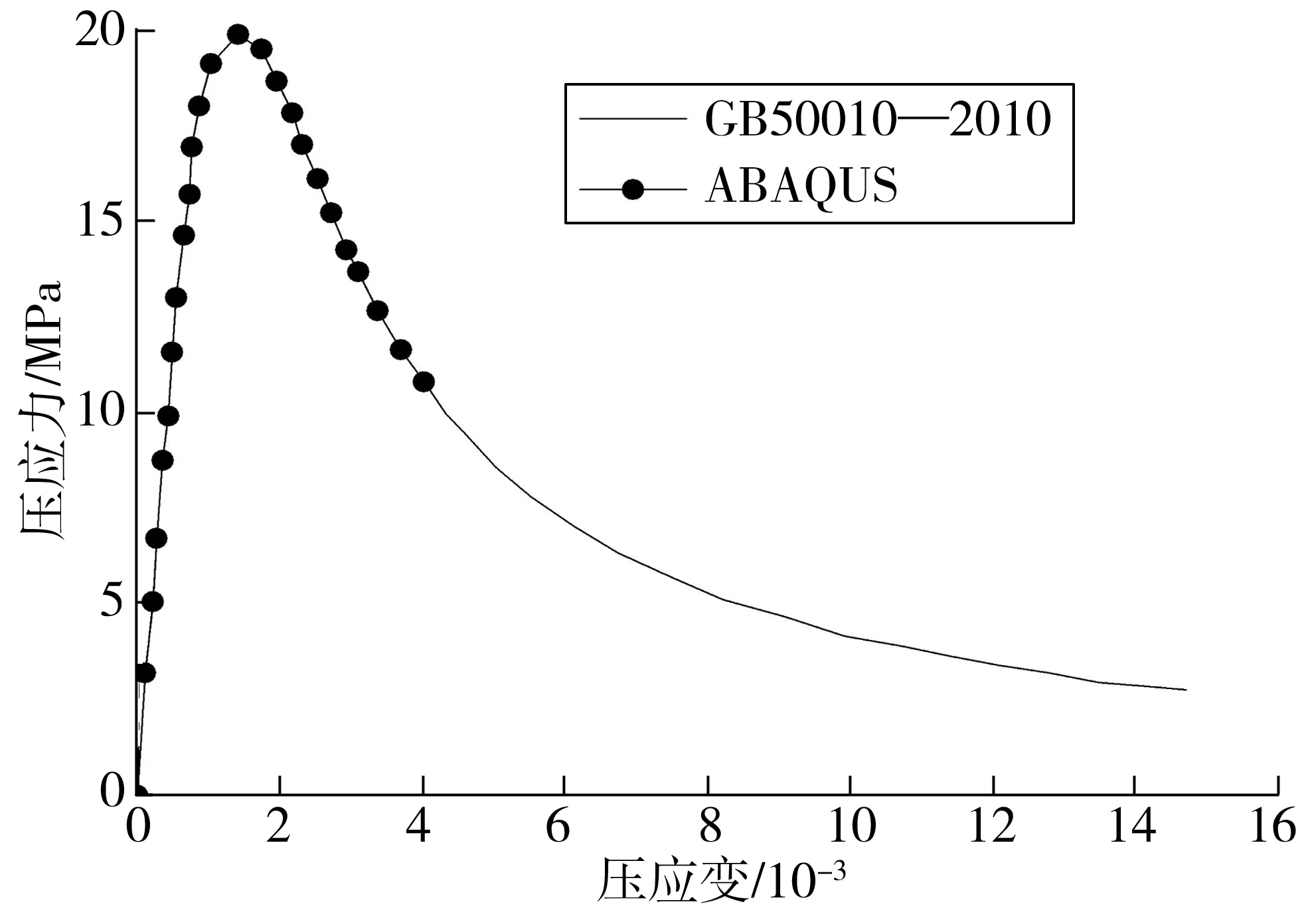
图4 单轴压缩荷载曲线与单轴理论应力-应变曲线Fig. 4 Uniaxial compression load curve and uniaxial theoretical stress-strain curve
1.3 边界条件模拟及地震动输入
在进行动力计算时,为充分考虑远场地基介质辐射阻尼效应,需要对模型施加人工边界条件,从而模拟无限地基介质对近场区域的影响。
如图5,笔者采用的人工边界为二维黏弹性人工边界[13],即在ABAQUS explicit求解器下使用spring-A以及阻尼原件并联并通过合理设置参数以达到清除反射、模拟透射的目的。

图5 二维黏弹性边界Fig. 5 2D viscoelastic boundary
施加黏弹性边界后,在模型底部输入地震荷载。输入的地震荷载采用1995年在神户气象台记录的日本阪神(kobe)地震波,并以0.6倍的水平向地震动作为竖直向地震动的输入值,如图6。为精简计算过程,提升计算的效率,在本次数值模拟过程中取幅值波动较大的前24 s作为输入荷载作用于模型底部。

图6 地面运动加速度时程Fig. 6 Time history of ground motion acceleration
1.4 监测点设置及中柱端部位移响应
考虑初始重力场,进行地应力平衡后采用水平与竖向地震动耦合作用的波动输入方式进行动力计算。如图7,分别设置监测点A、B。通过计算可以得到对应二维有限元模型底部时A、B两点的水平、
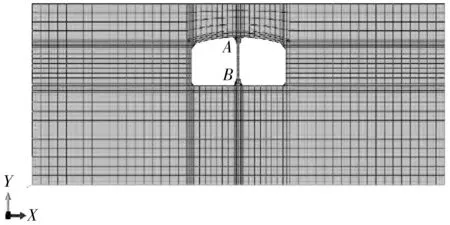
图7 监测点位置Fig. 7 The position of monitoring points
竖直位移时程曲线。将各时刻两点的水平、竖直位移做差得到不同截面形状下中柱端部相对位移响应曲线,如图8。将此相对位移时程曲线作为三维中柱模型的输入荷载。
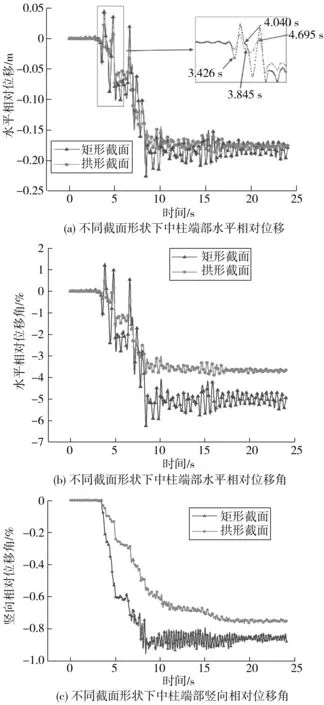
图8 不同截面形状下中柱端部相对位移响应Fig. 8 Relative displacement response between two ends of the mid column with different cross-section shapes
图8中,位移角=相对位移/中柱高度。由图8可以看到,总的来说两种截面形状下A、B两点的相对位移响应规律基本一致,尤其是在相对水平位移响应规律中仅有幅值上的区别,而拱形界面的相对竖向位移开展较之矩形截面更加平缓,这对发挥结构延性是有好处的。
虽然发展规律比较相似,但幅值的大小会影响混凝土进入塑性的时间与比例,最终决定结构的工作状态与受力模式。总体来看,在0~3.3 s期间,A、B两点的相对水平位移发展较为稳定,在3.5~4.8 s期间有一段短暂且相对稳定的往复运动,推测此时在柱的一定高度范围内,两侧均有部分混凝土进入塑性区,甚至出现剥落,从而形成一个旋转刚度较小的塑性铰,塑性铰以上部分可以在小阻力下绕铰做相对稳定的旋转运动。结构在3.3~8.3 s期间受强烈的地震作用而逐渐向一侧累积塑性变形。实际地震发生过程中,当塑性变形积累到一定量值后,中柱结构会因无法承受顶板竖向荷载产生的剪力而发生破坏,进而退出受力,顶板跨径剧增,最后因无法承受巨大弯矩而被折断。
2 三维中柱精细化有限元模拟
2.1 中柱精细化模型建立
除三维整体有限元模型外,再建立矩形截面与拱形截面下中柱的精细化模型如图9(a)。模型底部的约束形式为限制坐标系3个方向的位移,中柱截面的纵向受力钢筋分布形式如图9(b),截面尺寸为0.40 m×1.00 m,柱高分别为3.62 m(矩形截面)和4.79 m(拱形截面),纵筋按照大开车站的实际布置形式取30根32 mm的螺纹钢筋。
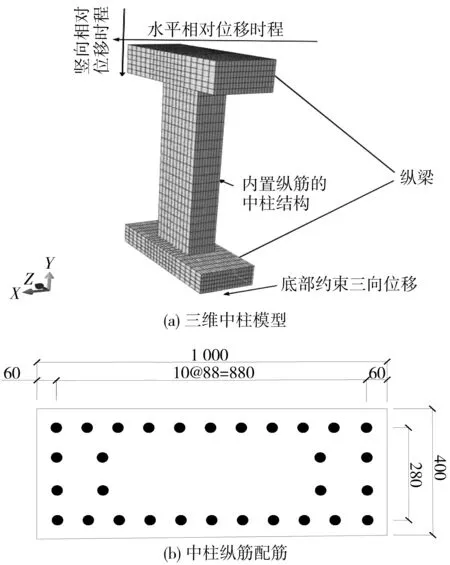
图9 三维中柱模型(单位:mm)Fig. 9 3D mid-column model
2.2 材料参数及本构模型
对于中柱精细化模型,仍采用Mohr-Coulomb模型来描述土的变形特征。中柱结构延用1.2节中混凝土塑性损伤模型,中柱内纵向受力钢筋采用Mises理想弹塑性本构模型,其中ρ=7.8 g/cm3,E=200 GPa,泊松比为0.1,屈服应力为240 MPa,采用内置区域方式与主体结构连接。两端连接的梁部分采用线弹性模型,弹性模量与1.2节所述其他主体结构保持一致,保证混凝土结构的刚度,从而起到传递位移荷载的作用。
3 结果分析
3.1 矩形截面中柱精细化模拟结果
矩形截面计算结果如图10~图11,图10(a)、图11(a)计算得到的混凝土塑性应变临界值为2.62×10-4;图10(b)、图11(b)为位移云图,采取的缩放比例为30。将图8的位移时程施加在三维精细化中柱模型顶部后的前3.2 s内,中柱结构基本没有发生屈服现象;在3.200~3.462 s期间中柱仅有底部以及顶部有小范围区域的混凝土进入屈服状态;在3.462 s之后中柱结构的塑性变形逐渐积累,达到屈服强度的混凝土出现开裂现象,并于4.04 s在中柱底部首次出现了变形峰值,变形区钢筋屈服,外部混凝土出现一定规模的开裂并有部分混凝土出现剥离现象,中柱整体刚度受此影响急速下降,中柱的变形迅速加剧,中柱的承载性能逐渐下降。由于钢筋在扭曲状态下的承载能力远小于直线状态,在高轴压比条件下,中柱结构发生进一步的破坏,进而使顶板中心挠度增大,导致弯矩迅速累积,最终不堪重负而被折断,车站结构发生整体性失稳。

图10 矩形断面车站3.462 s时刻响应云图Fig. 10 Cloud diagram of 3.462s time response of station with rectangular section
3.2 拱形截面中柱精细化模拟结果
矩形截面计算结果如图12~图13。与矩形截面下的中柱模型相比,拱形截面下的中柱屈服时刻与首次屈服位置出现了明显的变化,在相同地震作用的影响下,拱形截面下中柱混凝土出现区域性屈服的时刻发生了明显的后延,首次出现变形峰值的时刻与位置也发生了变化,在强烈震动区段,中柱并未像矩形截面下的中柱一般出现大变形区域,中柱形态良好,扭曲的程度较轻。总体来说,拱形截面下中柱混凝土的屈服范围与屈服程度较之于矩形截面要更加小和轻,中柱承载性能的发挥没有受到根本性的影响,中柱的承载环境维持在一个相对良好的状态,为保持车站结构的整体稳定提供了有力保障。

图11 矩形断面车站4.04 s时刻响应云图Fig. 11 Cloud diagram of 4.04s time response of station with rectangular section

图12 拱形断面车站3.845 s时刻响应云图Fig. 12 Cloud diagram of 3.845s time response of station with arch section

图13 拱形截面4.695 s累计塑性应变和位移Fig. 13 Cloud diagram of 4.695s time response of station with arch section
3.3 震后结果对比
整个过程与二维模型的结果吻合的比较好,中柱结构首次出现大范围屈服的时刻3.462、3.845 s与二维整体分析得到的水平相对位移峰值时刻3.47、3.79 s比较接近,三维中柱模型出现变形峰值的时刻4.04、4.695 s也与图8中的位移峰值相对应,其中矩形截面为体现变形程度,选取的时刻稍有延后。图14(a)、图14(b)分别为矩形截面与拱形截面中柱内钢筋震后的应力分布情况,图14(c)为1995年阪神地震中大开车站内破坏的中柱。将图14(a)与图14(c)中的中柱情况进行对比,可以发现图14(a)中出现应力集中的位置与图14(c)中阪神地震作用下大开车站内中柱的破坏位置非常吻合,部分钢筋最终承受拉应力的破坏结果也符合实际情况,这表明本次模拟的结果与真实情况吻合的比较好。将图14(a)与图14(b)进行对比可以发现,与矩形截面下中柱内的钢筋应力分布不同,拱形截面下中柱内部的所有钢筋在地震作用后仍保持着承受压应力的状态,这表明地震作用未改变中柱结构的基本受力模式,中柱结构仍保持着持力状态,未因地震荷载作用而发生破坏,退出受力;反观矩形截面下中柱内的钢筋应力分布,部分钢筋的受力形式发生了转变,中柱结构部分混凝土在地震作用下被压碎,失去混凝土的约束后,混凝土压碎处钢筋的受力形式由轴向受压形式转变为剪压形式,从而使部分钢筋无法发挥其承受轴向荷载的能力,在剪压作用下发生大幅变形,退出受力,进而导致中柱结构发生破坏,无法继续保持持力工作。基于上述分析可得结论,拱形截面下中柱的延性及受力形态要优于矩形截面。


图14 模拟结果与实际震害模式对比Fig. 14 Comparison between simulation results and actual earthquake damage model
按照学者们对抗震延性设计的普遍认识,在截面和截面材料特型均相同的条件下,柱越高,具有的位移延性系数越低,柱顶的位移延性系数随中柱长细比的增大而减小。但延性系数低并不意味着变形能力弱,长细比小的柱抗力要更大,即更“刚”,而长细比大的柱则延性要更好,一个结构或构件可能有较大的变形能力,但它实际可利用的位移延性系数却可能较低。
需要注意的是,结构的整体延性与结构中构件的局部延性密切相关,如果设计不当,即使个别构件的延性很高,但整体的延性却可能非常低。
3.4 不同截面下中柱及侧墙的地震反应
不同截面形式车站的二维模型下,车站内中柱承受竖向荷载占结构承受总体竖向荷载的比例随时间的变化曲线如图15。由于真实情况下中柱需承受一跨范围内(3.5 m)的竖向荷载,而二维模型相当于是按纵向1 m的情况进行计算的,所以承受的荷载与地震作用过程中顶板上覆土的惯性力效应[9-10]的发挥程度是不一样的,最终的结果也存在一定的偏差。从规律上看,拱形截面下中柱承受竖向荷载的比例较之矩形截面有所下降,这对提高中柱抵抗水平变形的能力是有好处的。二维模型中矩形截面与拱形截面下中柱震前轴力分别为1 093、927.5 kN,承受竖向荷载的平均比例分别为37.8%和36.2%,震中承受竖向荷载的平均比例分别取43%和33%,通过计算可得,在地震作用过程中采取拱形截面时中柱的平均轴力较之矩形截面要低32%左右。
中柱承受荷载的下降意味着侧墙承受荷载的提升,如图16,相比于传统矩形截面车站,地震作用下拱形截面车站内侧墙承受的动竖向荷载与静力作用下承受的静竖向荷载之比变化十分明显,拱形构造的顶板对侧墙的内力响应产生了显著的影响。
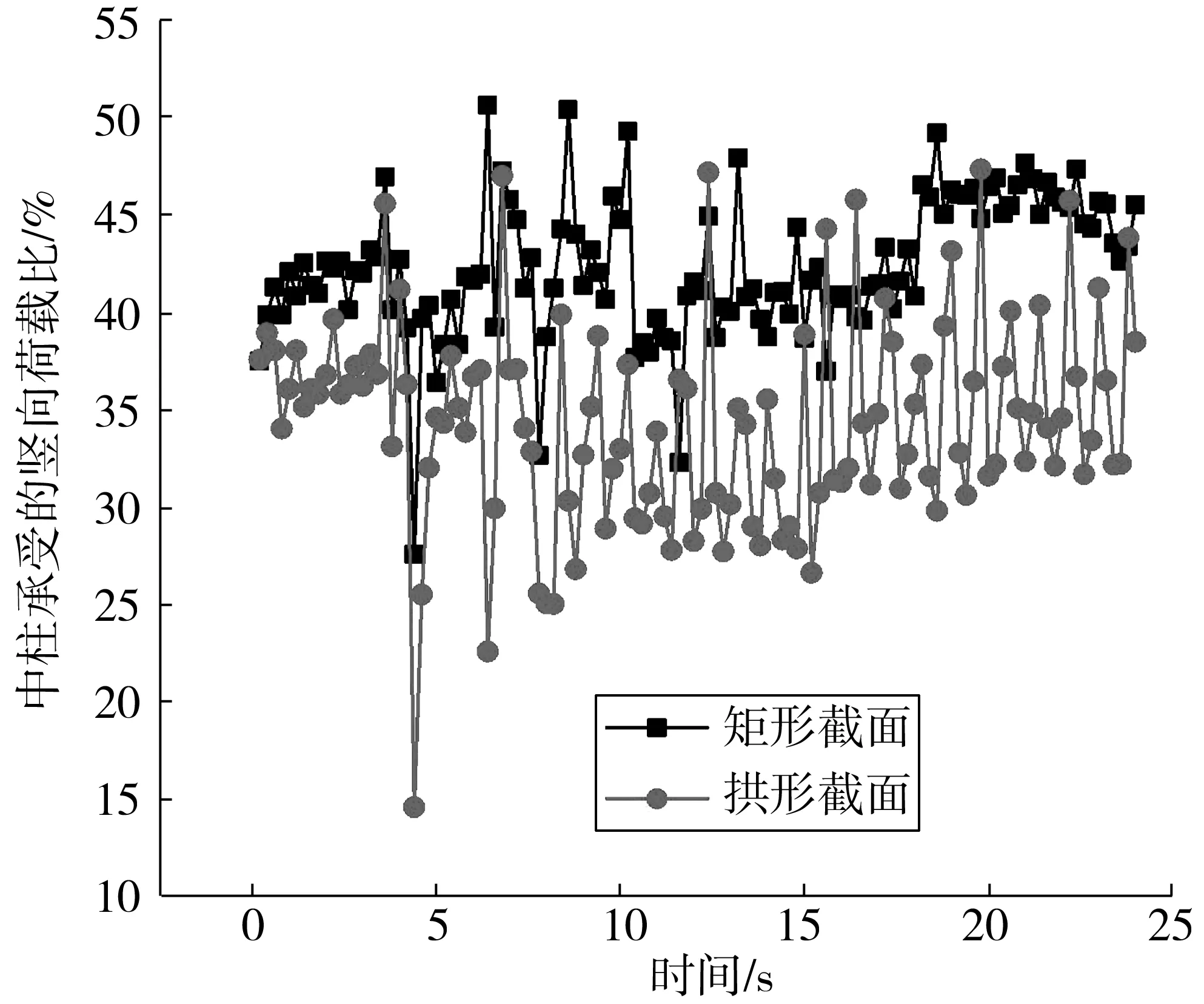
图15 不同截面形状下中柱承受的竖向荷载Fig. 15 The vertical load on mid-column with different cross-section shapes
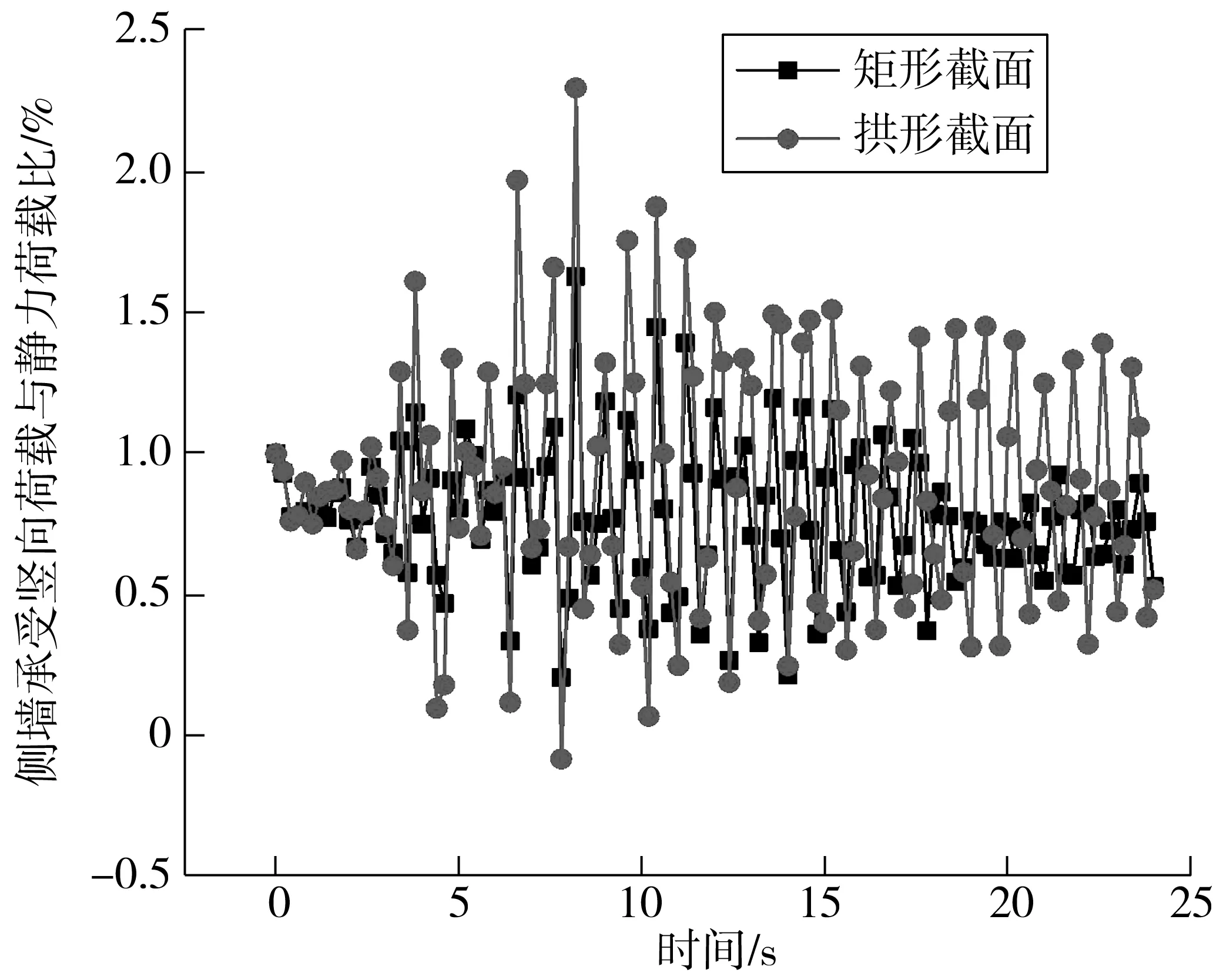
图16 不同截面形状下侧墙承受的竖向荷载Fig. 16 The vertical load on side wall with different cross-section shapes
4 结 论
以日本阪神地震中大开车站的严重破坏为分析背景,通过二维整体有限元计算获得了不同截面形式车站在水平地震与竖直地震耦合作用下中柱端部的相对位移时程响应,再将此结果作为输入荷载施加在精细建模的三维中柱模型顶部,再现了大开车站内的中柱在地震作用下的破坏过程。通过对比不同车站截面形式下中柱力学性能的变化过程、承受竖向荷载的比例变化情况以及震后钢筋的受力特性,验证了通过改变车站截面形状改善车站关键构建受力环境的可行性以及有效性。研究结论如下:
1)模拟结果表明:通过改变车站的截面形状可以明显改善中柱在地震作用中的受力环境,采用拱形截面有利于维持中柱良好的持力状态。
2)拱形截面的布置形式不仅改变了顶板对竖向荷载的分配方式,还减少了车站上覆土的重量(约19.8%),使得地震作用过程中中柱结构的高轴压工作环境有所缓解(约下降32%);同时增大了中柱的长细比(约32.3%),从而增强了中柱的延性。
3)拱形截面下中柱端部的位移响应形式虽然与矩形截面大体相近,但幅值要更小,前6 s内矩形截面比拱形截面下同一时刻的幅值要高出25%~300%,且拱形截面下响应曲线更加平滑,这对于发挥中柱结构的延性是有好处的。
4)结构的整体延性与结构中构件的局部延性密切相关。将车站结构作为整体,则中柱这一构件的局部延性就应成为抗震设防的重点,而将中柱作为整体,中柱中延性较差,容易发生破坏的部位就应该受到重点关注,比如柱端部应该进行特殊加固,中柱应增加环向钢筋以约束纵筋变形等。
5)对于侧墙结构在不同车站截面形式下的受力特征没有进行太过详细的分析,仅收集了竖向荷载的变化情况,而拱形截面势必会使侧墙的受力形式发生明显改变,因此会在下一步工作中以侧墙结构为研究重点,以研究改变车站截面形状对侧墙结构的影响。

