一种基于区域公平和污染治理差异的水污染负荷分配方法的介绍

黄晓敏,徐成剑

(长江勘测规划设计研究有限责任公司，武汉 430010)

引 言

《国务院关于印发水污染防治行动计划的通知》(国发〔2015〕17号)第二十条明确提出“未达到水质目标要求的地区要制定达标方案，将治污任务逐一落实到汇水范围内的排污单位”。对于涉及多区域、多类型污染源的水体，如何确定各区域和各污染源的削减率是水污染防治工作亟待解决的重要内容之一。

近年来众多学者陆续尝试提出兼顾公平性和经济最优性的水污染负荷分配方法。李如忠[1]等基于以综合基尼系数作为公平性目标，以污染物削减费用最小作为经济最优性目标，构建了基于双目标的水污染负荷分配方法；该方法将每个子区域“虚拟”为一座污水处理厂，每个子区域内水污染负荷的削减均由“虚拟”污水处理厂承担，削减费用即为“虚拟”污水处理厂的处理费用；该方法提出了一种可行的概化污染物削减费用的思路，但在污染物削减费用函数中并未考虑不同污染源废污水特点和治理费用的差异。罗军刚[2]等提出了一种双层多目标优化水污染负荷分配方法，其中，上层基于环境基尼系数最小和单位污染物排放成本最低对水污染物在区域间进行分配，下层基于工业产值最大和削减率不均最小对水污染物在排污单位间进行分配；该方法较好地考虑了区域及排污口两个等级的水污染物分配，以污水处理成本和水环境保护税税额来表征污染物排放成本，同样未细化不同污染源治理成本差异。本文在借鉴已有成果的基础上，对各污染源治理成本进行了调研和总结，提出了一种基于区域公平和污染治理差异的水污染负荷分配方法。

1 方法介绍

1.1 区间公平函数

参考王媛[3]、李如忠[4]等学者的研究成果，采用综合基尼系数作为区域公平函数。综合基尼系数公式为：

(1)

式中，G为综合基尼系数；Gj为基于某个指标j的基尼系数；wj为第j个指标的权重；m为指标的个数。

基尼系数[5]是由意大利经济学家基尼于1992年首次提出，最初用于考察居民收入分配差异状况。如图1所示，绝对平等分配曲线和实际分配曲线(即洛伦兹曲线)间面积计为A，实际分配曲线以下面积计为B，将A/(A+B)作为衡量贫富差距的标准，即为基尼系数。基尼系数越大，分配越不平均[6-7]。国际上通常把0.4作为收入分配贫富差距的“警戒线”[8]。参考国际惯例本文将水污染物分配的临界值，取值为0.4。

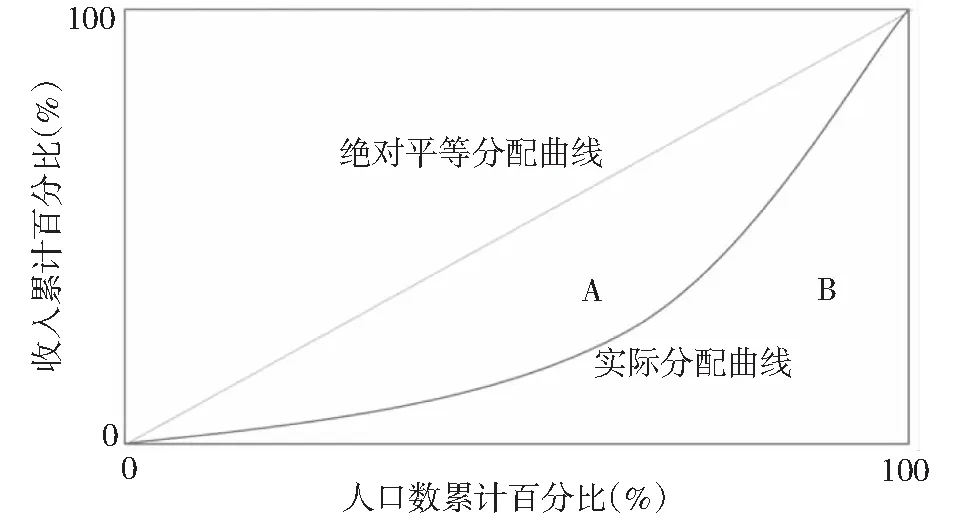
图1 基尼系数示意图Fig.1 Sketch of Gini coefficient

表1 基尼系数及其表征平均程度Tab.1 Gini coefficient and its average degree of characterization

基尼系数可采用梯形面积法计算，其公式为：

(2)

(3)

(4)

式中，Gj为基于某个指标j的基尼系数；Xj(i)为指标j的累计百分比；Mj(i)为第i个分区内j指标值；Yj(i)为指标j的污染物入河量累计百分比；Wj(i)为第i个分区内j污染物的入河量；n为分配区域的个数；当i=1时，(Xj-1,Yj-1)视为(0,0)。

指标是影响水污染物分配的重要因素[4]。指标的选取需综合考虑典型性、可获取性、易定量性、具有比较性等原则[3]。根据以上原则，本文确定常住人口、总产值和耕地面积作为代表性指标。

参考王媛[9]、李如忠[4]、张志辉[10]等研究成果，采用信息熵法确定各指标权重，确定方法如下：

yij=xi/zij

(5)

(6)

(7)

(8)

式中：xi为第j个分区内分配的最大允许污染物入河量；zij表示第i个分区内第j个指标的实际值(分别为常住人口、生产总值和耕地面积)；yij为第i个分区内第j个指标的单位负荷污染物量；pij为第j个指标、第i个分区的单位负荷污染物量所占权重；ej为第j个指标的单位负荷污染物量的信息熵；wj为第j个指标的权重；n为分区的个数；m为评价指标的个数。

1.2 污染治理差异函数

本文在调研各污染源治理的基础上，提出了综合治理费用作为污染治理差异函数。综合治理费用公式为：

(9)

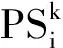
实际工作中，通常以废污水处理量来核算废污水处理费用。为便于落实每种污染负荷分配，本文将治理费用分摊至主要污染物。

1.2.1 吨水治理费用

根据水污染防治工作需求，本文调研分析了工业废水、散排城乡生活污水和已建污水处理厂尾水等三种污染源类型的吨水治理费用。

1.2.1.1 工业废水

参考《工业废水和城市污水处理技术经济手册》[11-12]费用方程，确定工业废水的吨水治理费用为：

NC工业=(Y2+M×Y3)×(1+i′)n′

(10)

式中：NC工业为工业废水吨水治理费用(元/t)；Y2为运行费用(元/m3水)，包括能耗费、折旧费、原材料费、维修费、工资、管理费和其他费用；Y3为电耗费用(度/m3水)，即设施运行过程中的用电量；Q为设计处理水量(m3/d);M为当地电费单价(元/度)；i′为物价上涨率5%；n′为《工业废水和城市污水处理技术经济手册》采用基准年至今年限。

1.2.1.2 散排城乡生活污水

参考牛坤玉[13]等研究成果，采用固定弹性模型法分析散排城乡生活污水的吨水治理费用。

执行不同排放标准的城乡生活污水处理运行费用估算方法为：

(11)

执行不同排放标准的城乡生活污水处理设施投资费用估算方法为：

(12)

1.2.1.3 已建污水处理厂提标改造

采用固定弹性模型法分析污水处理厂排放标准提高所增加的吨水治理费用。

+(el+k×Dh-1-el+g×Dh-1)/365*20

(13)

+(el×Dh-1-el+k×Dh-1)

(14)

+(el×Dh-1-el+g×Dh-1)

(15)

1.2.2 单位污染负荷治理费用

参考张鸣[14]的研究成果，采用处理设施效益值法对废污水主要污染物的治理成本进行核算，公式如下：

(16)

(17)

(18)

式中：ηl废水处理设施对第l种污染物的处理效益；Il废水处理设施第l种污染物的进水浓度(mg/L)；El废水处理设施第l种污染物的出水浓度(mg/L)；Sl第l种污染物的排放标准(mg/L)；βl废水处理设施第l种污染物的处理费用系数；Q为设计处理水量(m3/d);Cl废水第l种污染物的处理费用，(元/t)；NC废水的吨水处理费用，(元/t)；np污染源种类。

1.3 约束条件

水污染分配需要满足三个约束条件，即，总量控制约束、公平性约束和削减率约束[15]。

1.3.1 总量控制约束

总量控制约束包括区域分配总量约束和污染源分配总量约束两个方面。以各水功能区限制排污总量作为总量控制目标，并据此确定每种污染物的区域和污染源削减率。

(19)

(20)

WDi=(1-qdi)×PDi

(21)

(22)

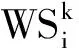
1.3.2 公平性约束

优化确定的综合基尼系数不大于优化前综合基尼系数，公平性不会变差。

G≤G0

(23)

式中：G为优化后综合基尼系数；G0为现状综合基尼系数。

1.3.3 削减率约束

根据各水功能区的总量控制目标，首先确定水功能区污染物总削减率。同时结合各污染源治理水平的差异，在技术可行和经济合理条件下，为各污染源设定污染物入河量削减率上限和下限。

(24)

(25)

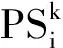
1.4 多目标问题求解

本文基于多目标粒子群优化(MOPSO)[16～20]算法对以综合基尼系数最小和综合治理成本最低为目标函数、以总量控制、公平性不变差、削减率技术可行经济合理为约束条件的水污染负荷分配问题进行求解。MOPSO初始种群为50，进化代数为50，变异概率为1。

2 应用案例

2.1 流域概况

十八河是毕节市七星关区在六冲河左岸的二级支流，发源于七星关区长春堡镇苏木寨，经镇龙潭、庙山营、龙潭边，至鸭池镇汇入白甫河。集水面积172km2，河长29.0km。十八河划分为两个水功能区，即十八河七星关区源头水保护区和十八河七星关区开发利用区。

十八河七星关区源头水保护区涉及河长约5.3km，沿线没有大的村镇分布，水质管理目标Ⅱ类，现状水质为Ⅱ类。

十八河七星关区开发利用区的二级水功能区为十八河七星关区农业、工业用水区，河长23.7km。此河段汇水范围涉及长春堡镇、千溪乡、朱昌镇和鸭江镇，沿线分布食品公司排污口1处，现状水质为劣Ⅴ类，水质管理目标为Ⅲ类。

本文以现状水质超标的十八河七星关区农业、工业用水区为例，基于MOPSO算法求解兼顾乡镇公平与污染源治理差异的水污染负荷分配问题。该水功能区的评价指标为常住人口、生产总值和耕地面积，汇水区内涉及乡镇的评价指标详见表2。规划2025年主要污染物COD和NH3-N的入河量分别为623.22t/a和64.25t/a。COD和NH3-N限制排污总量分别为219.90t/a和18.57t/a。

表2 各行政区评价指标比例Tab.2 Percentage of evaluation indicators in each administrative region (%)

2.2 污染物治理成本估算

采用处理设施效益值法对十八河七星关区农业、工业用水区汇水区内单位废污水及主要污染物的治理成本进行核算。各污染源处理设施进水和出水浓度见表3，单位废污水及主要污染物治理成本见图3。

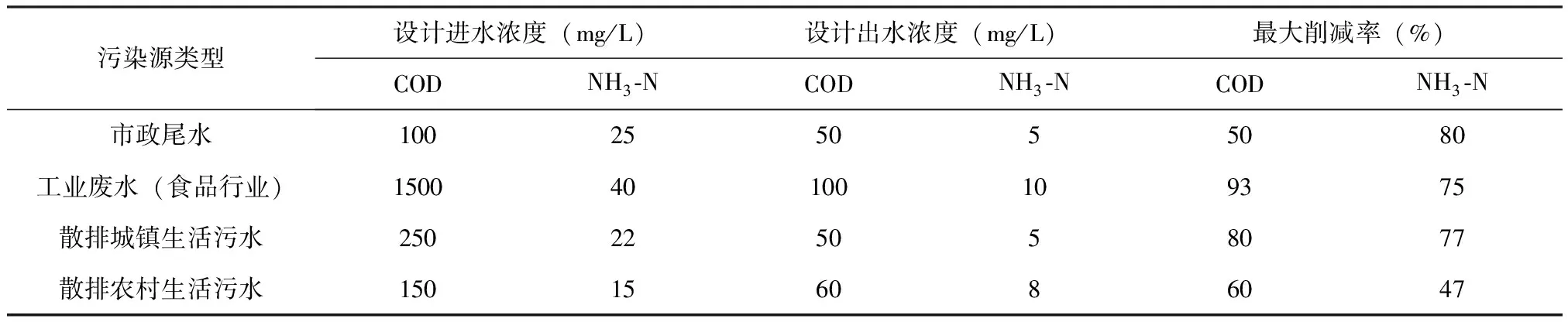
表3 处理设施进水和出水浓度Tab.3 Influent and effluent concentrations of treatment facilities

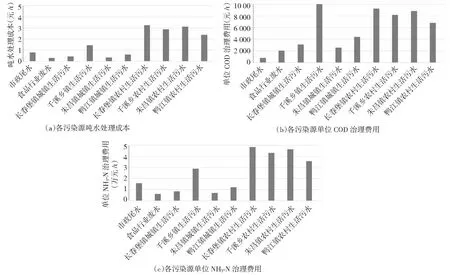
图2 各污染源单位污水及污染物治理费用Fig.2 Unit cost of sewage and pollutant

由图2可知，吨水处理成本和单位主要污染物治理费用受废污水处理难度和处理规模的影响。对于生活污水，千溪乡城镇生活污水处理规模较小，其吨水处理成本明显高于其他乡镇；农村生活污水具有分散分布、规模较小的特点，其吨水处理成本也明显高于城镇生活污水。案例中食品企业废水虽然污染物浓度较高，但其污染物削减率较高，折算后单位主要污染物治理费用低于生活污水的治理费用。

2.3 污染物负荷分配结果分析

基于MOPSO算法求解十八河七星关区农业、工业用水区兼顾区域公平和污染源治理差异的COD和NH3-N入河量分配解集见图3和图4。

图3和图4每个点均对应一个分配方案。COD入河量分配解集中，综合基尼系数变化范围0.3353～0.3425，综合治理费用变化范围38～422；NH3-N入河量分配解集中，综合基尼系数变化范围0.3472～0.3532，综合治理费用变化范围5314～86063。

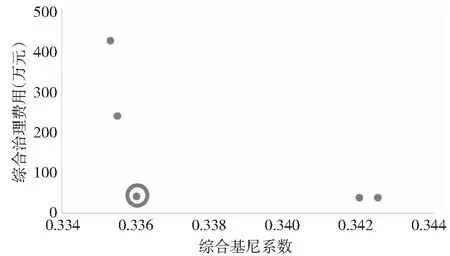
图3 COD多目标Pareto解集Fig.3 Multi-objective Pareto solution set of COD

选取综合基尼系数和综合治理费用相对较低的解作为代表分配方案进行分析，即图3和图4中红色圆圈标识解。以代表方案为例分析结果的合理性，结果详见表4和表5。

由表4可以看出，十八河七星关区农业、工业用水区优化后COD和NH3-N入河量分别为219.90t/a和18.57t/a，未超过限制排污总量，满足总量约束条件。

图4 NH3-N多目标Pareto解集Fig.4 Multi-objective Pareto solution set of NH3-N

表5中列出了优化前后各指标基尼系数变化情况。由表5可以看出，优化后主要污染物COD和NH3-N入河量的综合基尼系数较优化前均有所降低，公平性有所提高，满足公平性约束条件。

表4分析了各分区、污染源优化后COD和NH3-N入河量的削减率。与表5中最大削减率对比分析发现，优化后COD和NH3-N入河量的削减率未超过最大削减率，均满足削减率约束条件。

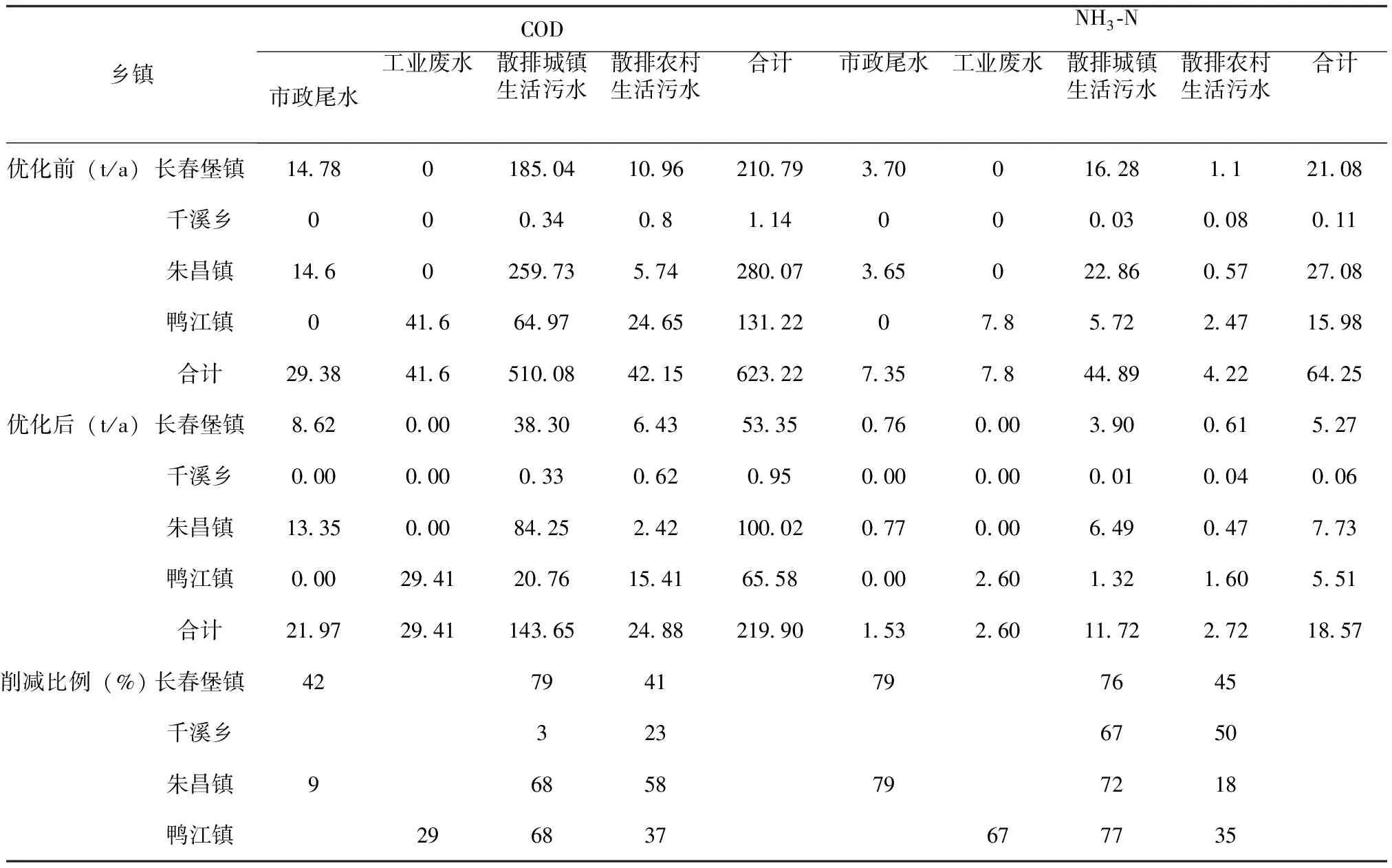
表4 COD和NH3-N入河量分配方案Tab.4 Distribution plan of COD and NH3-N inflow into the river

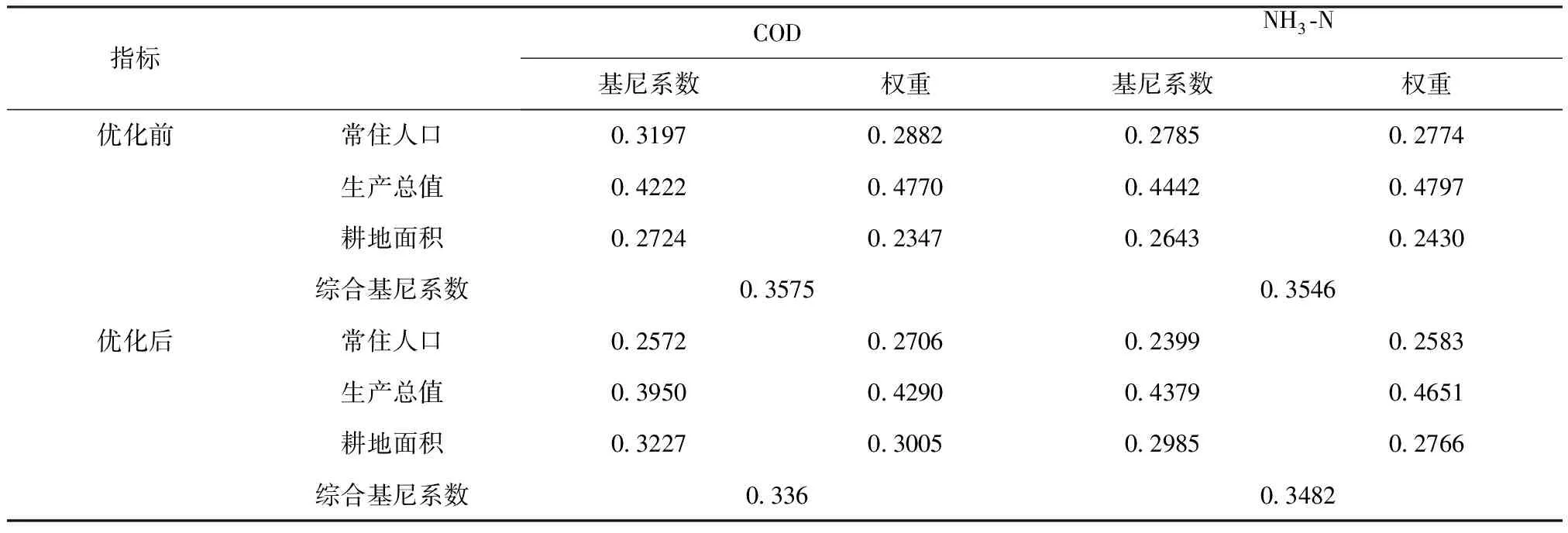
表5 各指标基尼系数变化对比表Tab.5 Comparison table of Gini coefficient variations of various indicators

通过案例分析发现，兼顾区域公平和污染源治理差异水污染负荷分配问题可通过MOPSO算法得到求解，结果满足总量、公平性和适宜削减率三方面约束条件，说明该分配方法可行。

3 结 语

通过对水污染负荷分配方法的应用和分析，总结如下：

3.1 总结了工业废水、散排城乡生活污水和已建污水处理厂尾水等污染源类型的吨水治理费用和主要污染物治理费用估算方法。

3.2 提供了一种兼顾区域公平和污染源削减差异的水污染负荷分配方法，并给出了约束条件设置和求解建议。

3.3 该方法可在排污权交易制度的建立和应用中发挥技术指导作用。