机器学习模型在切削力预测中应用研究

李香飞，张晓光，吴鸿雁

（天津职业技术师范大学工程实训中心，天津 300222）

0 引言

在研究材料的切削性能时，通常主要研究切削力与切削参数的关系特征，并基于不同计算方法建立切削力的预测模型。若是能够准确预测切削力，对于加工参数的优化和加工工艺的改善同样起着重要作用。

在切削力模型的建模中，经验公式有着广泛的应用。李峰[1]、吴明阳[2-3]和陈勇等[4]在研究镍基高温合金GH4169 的切削性能时，基于切削力经验公式建立了切削力预测模型，为高温合金GH4169 的粗加工插铣参数选取提供依据。张蓉蓉等[5]在研究铝合金7075 车削力时，使用指数公式建立了切削力预测模型，并证了模型的有效性。张晓[6]对3Cr13 不锈钢的铣削建模时，获取了Fx、Fy、Fz三个方向上的切削力，建立了切削力的经验模型，利用F值检验了模型的显著性。李素燕等[7]在高速车削淬硬轴承钢的切削力试验研究中，基于试验数据建立了经验模型用以切削力的预测。Jinfeng Wang 等[8]利用几何学和机械学结合建立了切削力回归模型用于对切削力的预测，利用试验数据验证了模型的预测可靠性。

由于近年来随着机器学习理论的不断完善和发展，基于这些成熟的机器学习理论生成的多种机器学习方法也被引入了切削力预测以及切削参数的优化研究中，大大提高了模型预测精度。高东强等[9]使用遗传算法并基于MATLAB 中的遗传算法工具箱。向国齐[10]研究钛合金铣削加工性能时，通过有限元数值计算建立了基于支持向量机的切削力预测模型。刘维伟[11]使用了多元线性回归方法，并通过实验验证了模型的预测准确性。胡敏敏[12]等研究钛合金TC4 的切削性能时，采用响应曲面法和神经算法结合的方法建立了切削力模型。李鑫[13]等在预测切削力时，分别基于铣削力的经验公式和人工神经网络的建立了切削力预测模型，通过比较发现基于人工神经网络的预测模型的预测精度优于经验公式。邓洁勇[14]等人研究钛合金的切削力时，使用BP神经网络建立了钛合金的切削力预测模型。Zoran Jurkovic 等[15]比较了在高速车削方式下支持向量机、神经网络以及多项式回归的预测性能，对于切削力和表面粗糙度的预测，支持向量机和多项式回归的预测性能没有明显差别，但二者优于神经网络，而对于刀具寿命方面的预测，神经网络的预测性能优于其他两种方法。

机器学习算法大多需要通过试验样本数据以便进行训练建模，但是在建模过程中不同算法对试验方法、试验数据等多种因素的敏感度不同，较为敏感的算法在不同场合建模时，其所建模型的预测精度千差万别。另外由于机器学习为暗箱建模过程，实验成本较高，数据样本容量较小，机器学习训练样本不够导致建模精度低等问题。因此合理的选择机器学习算法及样本容量较小的情况下对提高模型预测精度显得极为重要。然而在众多的文献中，鲜有对机器学习模型在小样本容量情况下的建模进行研究及对多种机器学习方法之间的预测性能进行比较，在机器学习方法建模和选择上缺乏参考。本文选取多篇文献中的切削力试验数据，这些试验数据中的试验材料、试验方法、切削方式以及输入变量等多个因素不尽相同。选取6 种机器学习方法分别对其建立切削力预测模型，并评估和比较各模型的预测精度。

1 样本数据说明

将文献中的数据基本信息整理成表1。样本数据主要基于不同种材料和不同的切削方式。李锋等[1]采用三因素分别是切削速度Vc、每齿进给量fz、径向切深ae，并获取了3个Fx、Fy、Fz三个方向上的切削力数据作为输出变量。高东强等人分析了主轴转速n（r∕min），每齿进给量fz（mm ∕z）以及径向切深ae（mm）对径向力Fa和轴向力Fz、刀片寿命的影响。刘维伟[11]和吴明阳等[2-3]均以切削速度Vc、背吃刀量ap和每齿进给量fz作为3 个输入变量。陈勇等[4]在研究高压冷却的环境下高温合金GH4169的加工切削力特性，以切削速度Vc、进给量f和径向切深ae为输入变量，以3个Fx、Fy、Fz三个方向上的切削力为输出变量。胡敏敏等[12]在铣削方式下选取了Vc、ap和fz作为输入变量。

表1 切削力数据样本的特征

张晓等[6]在对3Cr13不锈钢的铣削试验时，选取的输入变量分别为切削速度Vc、每齿进给量fz、径向切深ae以及背吃刀量ap，设计了25 组四因素五水平的正交试验，获取了Fx、Fy、Fz三个方向上的切削力。李鑫等[13]设计了27 组正交试验，但所选因素为主轴转速n，每齿进给量fz以及背吃刀量ap，输出变量为合力F合。邓杰勇[14]、李素燕[7]、Jinfeng Wang[8]、Zoran Jurkovic[15]中试验所选用的输入变量均为切削速度Vc、进给量f和背吃刀量ap，所不同的是试验材料、样本容量以及输出变量。

2 方法

2.1 机器学习算法

机器学习算法非常多，根据先前研究中预测精度较好的学习模型[16]，选择6 种模型用于切削力的分析预测。线性回归模型（Linear）计算成本较低，能得出相应的显式表达式，但是线性回归建模对异常值较为敏感[17]。多元自适应回归样条（MARS）法实际上是建立多个分段线性回归模型，但相较于线性回归模型和神经网络模型，该回归模型考虑了自变量的交互作用。袋装多元自适应回归样条法（BMARS）[17]法通过从观测数据中抽取多个数据集，对每个数据集分别建立预测模型，再对由所建预测模型得到的多个预测值求均值，这样可以减小预测值的方差提高预测精度，尤其对于那些不稳定的预测模型，通过求均值减小方差使预测值更加的稳定。与偏最小二乘法类似的神经网络算法（NNet）利用中间层的隐藏变量即隐藏元进行建模。支持向量机（SVM）是一种比较稳健的回归建模技术，在建模时因不使用残差的平方而使大的异常观测值只能对回归方程产生有限的影响。随机森林（RF）是基于袋装法，将多个独立的强树回归模型进行集合后，这样其整体的方差要比组合前的单个树回归模型方差更小。

2.2 模型的过拟合与模型调优

机器学习模型具有很好的自适应性，能够对复杂的关系建立模型，但是在建模过程中会过于强调对建模数据的拟合，将每个样本特有的噪声也融入进模型当中，这会影响模型的预测精度。因此在建模时应该通过寻找最优的参数以便于降低甚至消除模型的过拟合现象提高模型预测精度。重抽样方法有很多如K折交叉验证、广义交叉验证以及Bootstrap 方法。Bootstrap 方法更适用于小样本，它是利用计算机反复地从原始数据集中有放回的抽取数据组成新的样本，进而得出均方根误差（RMSE）衡量模型预测精度。RMSE 是均方误差MSE 的平方根，与观测值单位相同，通常是认为预测值与观测值之间的平均距离[17]。

3 切削力回归模型的建立

基于R 平台的caret 包中包含线性回归Linear、袋装法（BMARS）、多元自适应回归样条MARS、支持向量机SVM、人工神经网络NNet 和随机森林RF 这6 种学习方法，使用这6 种方法分别对上述论文中各方向切削力建立回归模型，依据统计量R2保留大于80%的25个切削力模型，以确保模型有较高的预测精度，其中基于铣削加工方式的模型有9 个，基于车削加工方式建立的模型有16 个。通过程序算法获取两个重要的统计量：R2以及均方根误差RMSE 值，并根据每个统计量值大小进行排列，如图1和图2中Fx、F合模型。

图1 切削力Fx 6种学习模型的预测性能比较

图2 切削力F合6种学习模型的预测性能比较

图1 所示为基于文献［6］和文献［13］中的试验数据进行建模并同时获取了每个模型相应的R2和RMSE，置信水平0.95。横轴表示两个预测性能统计量，纵轴从最底端至最顶端依次为6 个机器学习模型。从图1 中看出，按照R2值从小到大进行排列，那么BMARS 和Linear以及MARS 的R2近乎相当且均大于0.95，依次排在第1、第2、第3 位次。在统计量RMSE 中，同样是BMARS、Linear及MARS三种模型的RMSE 值最小。在模型的过拟合与调整过优中提到以RMSE 作为衡量模型的预测精度，RMSE 值越小这表明预测精度越高，那么在对文献[6]中数据进行回归预测时，BMARS 和Linear 及MRAS 模型的预测精度高于其他3 种学习方法，且BMARS 预测精度最高。同理在图2 中预测精度较好的是BMARS 和MARS 两种模型，其中BMARS 的模型精度最高。对于表1 中的其他样本数据也进行了如上的详细分析，由于篇幅限制，本文不列出详细计算结果。

4 结果分析

使用6 种机器学习方法对文献［1］至文献［13］切削力样本数据分别建立了25 个预测模型，以模型的评估精度统计量RMSE 值从小至大进行排列。基于同一切削力建立的回归模型，RMSE 值越小则表明该模型的预测精度越高，并排在第1位，RMSE值最大则意味着相应模型的预测精度在六者之中最低，排在第6 位。根据模型的顺次关系，统计出各方法分别排在第1位至第6位的频数绘制成如图3所示的直方图，横轴1，2，…，6表示第1至第6位次，即精度等级依次降低，纵轴为模型出现在某位次的频数。

图3 6种机器学习模型精度排序的频数直方图

图3中显示所建立的25个BMARS模型中，其主要分布在前4位，其中排在第1位的有13次，出现在前3位中共有20 次，占总数的86%。Linear 模型除了第6 位以外各位次都有分布，出现在第1 位2 次，第2 位5 次，分布在前3 位中有16 次，占总数的69%。MARS 主要集中分布在前3 位，处于第4 位和第5 位的次数只占全部的13%，出现在第1、第3 处均为5 次，并且多集中在第2位置，出现在前3 位的次数占总数的约86%。神经网络NNet 主要出现在第四位有10 处，并且在第1～5 处均有分布，出现在前3 位的次数占总数的约41%。随机森林RF 从排列上看，其精度相对较低，主要集中在第6 位处，出现在前3 位的次数占总数的约18%，并且在各位置处均有出现。支持向量机SVM 主要出现在第5 和第6位置处，少量出现在第4 位置处，未出现在前3 位置中。按第1～6 位出现的最大次数进行排列，则为BMARS、MARS、Linear、NNet、SVM和RF。

由上分析可知BMARS出现在第1位12次，远远超过MARS 的5 次，但从出现在前3 位中的总频次占比来看，BMARS 和MARS 相差不大，即6 种建模方法中，BMARS和MARS 所建的模型预测精度性能最好。另外从排列结果来看，线性模型Linear 相较于其他5 种非线性模型也有较好的表现，其预测精度多数情况下明显优于随机森林RF 和支持向量机SVM。另外线性回归和神经网络在6种方法中，它们的预测效果处于中档位置。

那么对于不同加工方式，这6 种方法的预测性能如何，使用同样的方法分别统计了各方法在1～6 位次出现的频数并绘制出如图4所示的直方图。

图4 6种机器学习模型在车削方式下的精度排序频数直方图

4.1 车削加工分析

在车削加工方式下，从图4 中可以发现，在16 个车削样本中，BMARS 以处在第1 位8 次居首，并且在第2、3 位均有分布，说明该方法对于不同的样本数据适应性比较高。Linear模型除了没有出现在第6位以外其余各位次均有分布，主要是不同的材料、试验方式及试验设计方法和样本量都会成为影响模型的预测性能，而Linear在6 个位次中均有出现说明Linear 对于不同的样本也体现出了不同的预测性能。MARS方法在前3个位次均匀分布，总体预测性能在6 种方法中表现较好。NNet 方法主要集中出现在第4位，多达9次，这主要是神经网络算法的预测精度会随着样本量增加而提高，在切削性能研究上，实际的样本量会相对较小，限制了该算法的预测精度。RF 方法在第6 位出现8 次，SVM 只出现在第5 和第6 位。从图中基本可以看出，在车削加工方式且样本小容量情况下，BMARS、MARS 预测效果要优于其他几种方法。

4.2 铣削加工分析

在铣削加工方式下，对8 个铣削力样本数据根据模型的RMSE 值进行排列后，统计出各方法出现在各位次的数量绘制出如图5所示的直方图，从图中可以看出，8个样本中，BMARS 方法5 次排在第1 位。排在第2 位次最多的是MARS，出现4 次。Linear 排在第3 位4 次。NNet 在各位次分别出现1～2 次。RF 主要出现在第6 位，SVM 也是在后3 个位次中均匀分布。因此可以看出在铣削加工方式和小样本容量下，6 种方法中BMARS 和MRAS表现较好，RF和SVM表现相对较差。

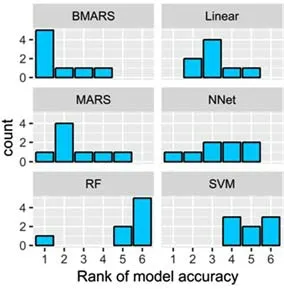
图5 6种机器学习模型在铣削方式下的精度排序频数直方图

5 结束语

使用6 种机器方法对不同切削方式，不同的输入变量以及不同方向的切削力进行拟合回归，选取RMSE 值作为衡量模型预测精度的依据，并据此进行排列。通过统计各方法在6 个位次中出现的频次，基本上可以看出对材料切削力的进行预测时，在车、铣两种加工方式中，同样是基于小样本数据，BMARS 和MRAS 相比较于Linear、NNet、RF、SVM 四种方法表现较好，并且对样本的适应性较强。同时Linear 算法作为所选用的算法中唯一的线性回归算法，其预测性能表现也相对较好。该结论可以为建立切削力预测模型时方法的选择提供参考和指导。